Introduction to Arrays Problem Input 5 scores compute

Introduction to Arrays • Problem: – Input 5 scores, compute total, average – Input 100. . . • Example – test scores, employees, temperatures 1

Array • structured data type • array ‑ group of variables referred to by one name, composed of elements • element or member – each item in the array – referred to by one name with an index: a[0], a[1], . . . • index or subscript – references array element 2

Array Declaration type name[size]; • type - type of each member in array – Can be of any type • name - name of the array • size - number of members in the array(constant) • Dimension each array before it is used, one time only 3

Example • float arr[20]; • float test. Scores[30]; Or declare size as a constant • const int MAX_TESTS = 100; • int tests[MAX_TESTS]; 4

C++ Examples int main() { float days[365]; char code[12]; int buf[100]; 5

Storage float test. Scores[10]; 6

Accessing Array Elements • reference array element using subscript or index • First element – subscript is 0 • Last element – subscript is one less than size – int buf[100]; – buf[0] - first element of buf – buf[99] - last element of buf • no checking for "Out of Bounds" 7

Valid subscripts • can use variables, expression, or constants as subscripts • angle[0] = 4. 93; • angle[1] = -15. 2; • val[i+2] = val[i] + val[i+1]; • x = val[j] • cout << score[k] <<score[k+1]<<score[k+2]; 8

Array elements • Each array element is treated exactly as a variable. buf[5] = 30 scores[1] = 95; i = buf[8] * 92; cout << buff[80]; if (a[i] < 14) cout << array [3]; x = y * nums[14]; cin >> sc[3] 9

Cannot operate on arrays as unit. • The following are invalid: array = 0; cout << scores cin >> arraya = arrayb; 10

Counted Loops and Arrays • counted loop - based on reaching a fixed number of repetitions for (initialize; test; increment) for (i = 0; i < 10; i++). . . 11

To read in an array: const int N = ? ; int test[N]; int index; for (index = 0; index < N; index++) { cout << "Enter test “ <<index; cin >> test[index]; } 12

Printing an array const int N = ? ; int test[N]; int index; for (index = 0; index < N; index++) { cout << test[index]; } Or with a label: cout << "test[“ << index <<"] is “<< test[index]; 13

To set the entire array to 0: const int N = ? ; int test[N]; int index; for (index = 0; index < N; index++) { test[index] = 0; } 14

To sum an array: const int N = ? ; int test[N]; int index; sum = 0; for (index = 0; index < N; index++) { sum = sum + test[index]; } 15

To print an array in reverse order: const int N = ? ; int test[N]; int index; for (index = N-1; index >= 0; index--) { cout << test[index]; } Or with a label: cout << "test[“ << index <<"] is “<< test[index]; 16

To copy one array to another: must have same # of elements int array 1[N], array 2[N]; for (index = 0; index < N; index++) array 1[index] = array 2[index]. 17

Reading any number of values into an array: string name [50]; //must allocate maximum size string temp. Name; int num. Names; num. Names = 0; infile >> temp. Name; while (infile && num. Names < 50) { name[num. Names] = temp. Name; num. Names = num. Names + 1; infile >> temp. Name; } 18

Multidimensional arrays • arrays can have any number of dimensions • Two dimensional – int hi. Temp[52][7]; – Must use two subscripts to access – hi. Temp[6][3] = 56. 6; • Three dimensional – int graph[10][20][30]; • etc. 19

float table[3][4]; 20

table[0][0] table[0][1] table[0][2] table[0][3] table[1][0] table[1][1] table[1][2] table[1][3] table[2][0] table[2][1] table[2][2] table[2][3] • Stored in row major order 21

Initialize int table[10][6]; int row, col; for (row = 0; row < 10; row++) for (col = 0; row < 6; row++) table[row][col] = 0; 22

Sequential or Linear Search • compares each element of the array with the search key. • works well for small arrays or for unsorted arrays • works for any table • slow 23

int Linear. Search(/*in */ int array[], int size, int key) bool found; int ix; found = false; ix = 0; while (ix < size && !found) { if (array[ix] == key) found = true; else ix = ix + 1 } if (found) return ix; else return -1; } 24

BINARY SEARCH • requires sorted list – (Ex: phone books, dictionaries). • keep dividing list in half, compare against middle argument • eliminates one half of the elements after each comparison. • efficient 25

Simple Binary Search Algorithm: • locates the middle element and compares it with the search key, till a match is found or no elements are left for comparison. • The array: 1 5 7 11 14 17 19 25 29 37 50 • How to search for x: 1. Compare with the middle element, m 2. If x = m, done 3. If x > m, continue searching in the right half 4. If x < m, continue the search in the left half 26

void Bin. Search( string list[], string item, int length, int& index, bool& found) { int first, last, middle; first = 0; // lower bound on list last = length - 1; // upper bound on list found = FALSE; while (last >= first && !found) { middle = (first + last)/2; if (item < list[middle] last = middle - 1; else if (item > list[middle]) first = middle + 1; else found = true; } index = middle; } 27

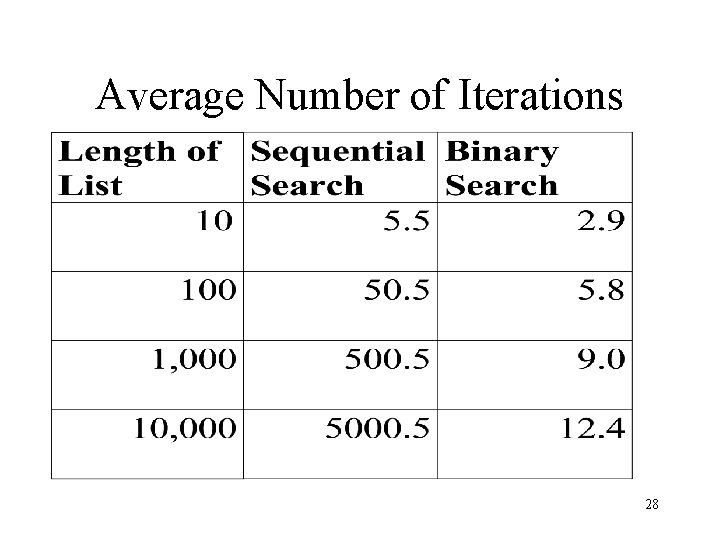
Average Number of Iterations 28

Records or Structures • aggregate data types • record - single variable name for the whole collection • composed of several variables - fields, BUT, unlike arrays, members also have names field names, and may be different types; • member 29

Declaration 1. define template - form of the structure; struct Record. Name type member_1; type member_2; … endrecord 2. Declare variable Record. Name varname; 30

Example: struct Employee { integer id. Number; string name; float salary; }; • essentially creates a new variable type Employee emp 1; Employee new. Emp; 31

Reference • use. Operator => record. Name. membername • example: new. Emp. id. Number = 527; cout << new. Emp. name; 32

Pointers • Contains the address of another memory location • Data. Type* Variable; • int* iptr; • & - address of • * - location pointed to by 33

int i; int* iptr; i. Ptr = &i; *iptr = 5; iptr i 5 34