Introduction to Arithmetic Sequences 18 May 2011 Arithmetic

Introduction to Arithmetic Sequences 18 May 2011

Arithmetic Sequences l l When the difference between any two numbers is the same constant value This difference is called d or the constant difference l l {4, 5, 7, 10, 14, 19, …} ← Not an Arithmetic Sequence {7, 11, 15, 19, 23, . . . } ← Arithmetic Sequence d=4

Your Turn: l Determine if the following sequences are arithmetic sequences. If so, find d (the constant difference). l l {14, 10, 6, 2, – 2, …} {3, 5, 8, 12, 17, …} {33, 27, 21, 16, 11, …} {4, 10, 16, 22, 28, …}

Recursive Form l The recursive form of a sequence tell you the relationship between any two sequential (in order) terms. un = un– 1 + d n≥ 2 common difference

Writing Arithmetic Sequences in Recursive Form If given a term and d 1. Substitute d into the recursive formula

Examples: Write the recursive form and find the next 3 terms l l u 1 = 39, d = 5

Your Turn: Write the recursive form and find the next 3 terms l u 1 = 8, d = – 2 l u 1 = – 9. 2, d = 0. 9

Writing Arithmetic Sequences in Recursive Form, cont. If given two, non-sequential terms 1. Solve for d d = difference in the value of the terms difference in the number of terms 2. Substitute d into the recursive formula

Example #1 Find the recursive formula l u 3 = 13 and u 7 = 37

Example #2 Find the recursive formula l u 2 = – 5 and u 7 = 30

Example #3 Find the recursive formula l u 4 = – 43 and u 6 = – 61

Your Turn Find the recursive formula: 1. u 3 = 53 and u 5 = 71 3. u 3 = 1 and u 7 = -43 2. u 2 = -7 and u 5 = 8

Explicit Form l The explicit form of a sequence tell you the relationship between the 1 st term and any other term. un = u 1 + (n – 1)d n≥ 1 common difference

Summary: Recursive Form vs. Explicit Form Recursive Form un = un– 1 + d l n ≥ 2 un = u 1 + (n – 1)d Sequential Terms l 1 st Term and Any Other Term n≥ 1

Writing Arithmetic Sequences in Explicit Form l l You need to know u 1 and d!!! Substitute the values into the explicit formula 1. u 1 = 5 and d = 2 2. u 1 = -4 and d = 5

Writing Arithmetic Sequences in Explicit Form, cont. l 1. 2. You may need to solve for u 1 and/or d. Solve for d if necessary Back solve for u 1 using the explicit formula u 4 = 12 and d = 2

Example #2 u 7 = -8 and d = 3

Example #3 u 6 = 57 and u 10 = 93

Example #4 u 2 = -37 and u 7 = -22

Your Turn: Find the explicit formulas: 1. u 5 = -2 and d = -6 2. u 11 = 118 and d = 13 3. u 3 = 17 and u 8 = 92 4. u 2 = 77 and u 5 = -34

Using Explicit Form to Find Terms l Just substitute values into the formula! u 1 = 5, d = 2, find u 5

Using Explicit Form to Find Terms, cont. u 1 = -4, d = 5, find u 10

Your Turn: 1. u 1 = 4, d = ¼ Find u 8 2. u 1 = -6, d = ⅔ Find u 4 3. u 1 = 10, d = -½ Find u 12 4. u 1 = π, d = 2 Find u 27

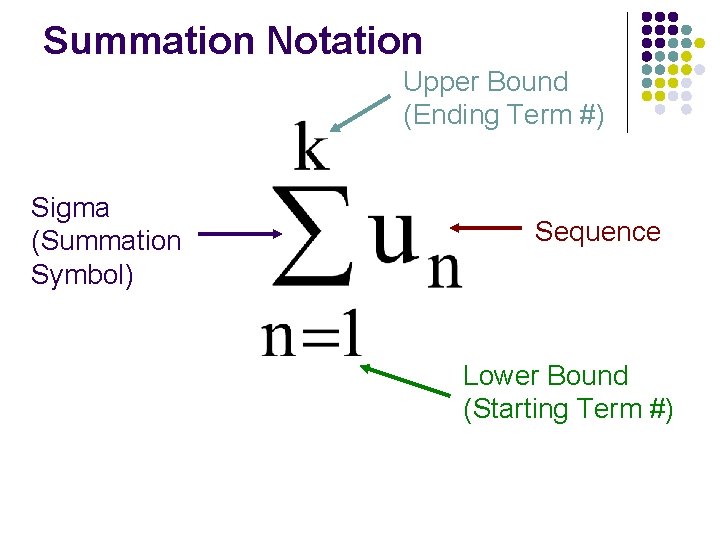
Summations l Summation – the sum of the terms in a sequence {2, 4, 6, 8} → 2 + 4 + 6 + 8 = 20 l Represented by a capital Sigma

Summation Notation Upper Bound (Ending Term #) Sigma (Summation Symbol) Sequence Lower Bound (Starting Term #)

Example #1

Example #2

Example #3

Your Turn: Find the sum:

Your Turn: Find the sum:

Your Turn: Find the sum:

Partial Sums of Arithmetic Sequences – Formula #1 l Good to use when you know the 1 st term AND the last term # of terms 1 st term last term

Formula #1 – Example #1 Find the partial sum: k = 9, u 1 = 6, u 9 = – 24

Formula #1 – Example #2 Find the partial sum: k = 6, u 1 = – 4, u 6 = 14

Formula #1 – Example #3 Find the partial sum: k = 10, u 1 = 0, u 10 = 30

Your Turn: Find the partial sum: 1. k = 8, u 1 = 7, u 8 = 42 2. k = 5, u 1 = – 21, u 5 = 11 3. k = 6, u 1 = 16, u 6 = – 19

Partial Sums of Arithmetic Sequences – Formula #2 l Good to use when you know the 1 st term, the # of terms AND the common difference # of terms 1 st term common difference

Formula #2 – Example #1 Find the partial sum: k = 12, u 1 = – 8, d = 5

Formula #2 – Example #2 Find the partial sum: k = 6, u 1 = 2, d = 5

Formula #2 – Example #3 Find the partial sum: k = 7, u 1 = ¾, d = –½

Your Turn: Find the partial sum: 1. k = 4, u 1 = 39, d = 10 2. k = 5, u 1 = 22, d = 6 3. k = 7, u 1 = 6, d = 5

Choosing the Right Partial Sum Formula Do you have the last term or the constant difference?

Examples l Identify the correct partial sum formula: 1. k = 6, u 1 = 10, d = – 3 2. k = 12, u 1 = 4, u 12 = 100

Your Turn: l 1. 2. 3. 4. 5. Identify the correct partial sum formula and solve for the partial sum k = 11, u 1 = 10, d = 2 k = 10, u 1 = 4, u 10 = 22 k = 16, u 1 = 20, d = 7 k = 15, u 1 = 20, d = 10 k = 13, u 1 = – 18, u 13 = – 102