Introduction to Architecture for Parallel Computing Models of

Introduction to Architecture for Parallel Computing

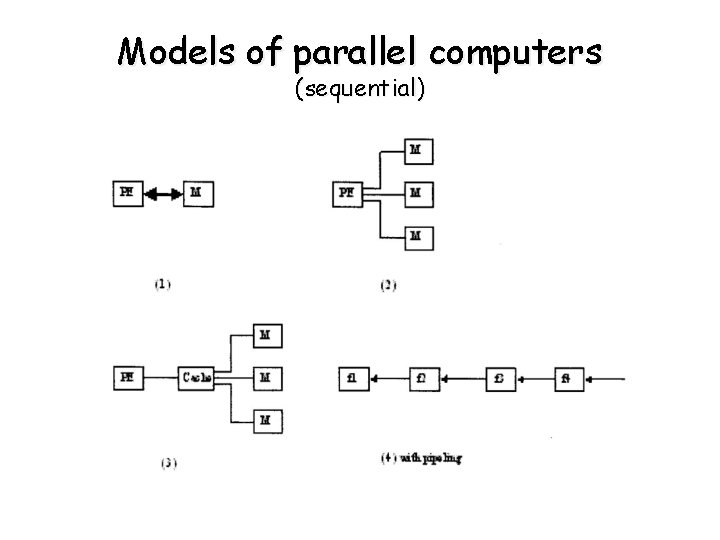
Models of parallel computers (sequential)

Taxonomy • • Control Address space Interconnection network Granularity Control • SISD – Single instruction stream, single data stream Pros: 1. Single program less memory Cons: 1. Dedicated hardware (expensive) 2. Rigid

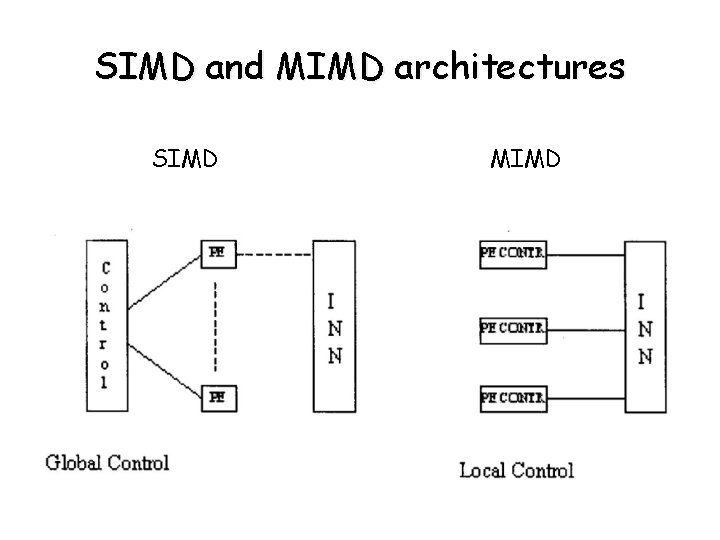
Taxonomy (continued) • SIMD – Single instruction stream, multiple data stream • MISD – Multiple instruction stream, single data stream • MIMD – Multiple instruction stream, multiple data stream Pros: 1. Over the shelf hardware – inexpensive 2. Flexible Cons: 1. Program and data on all PEs

SIMD and MIMD architectures SIMD MIMD

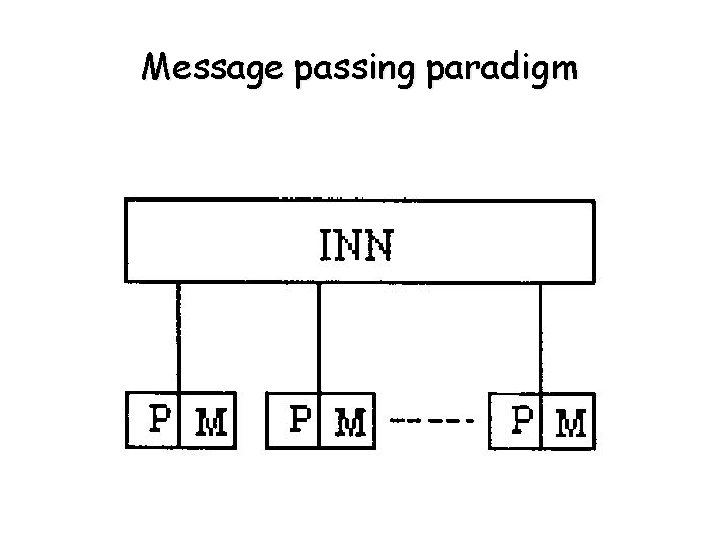
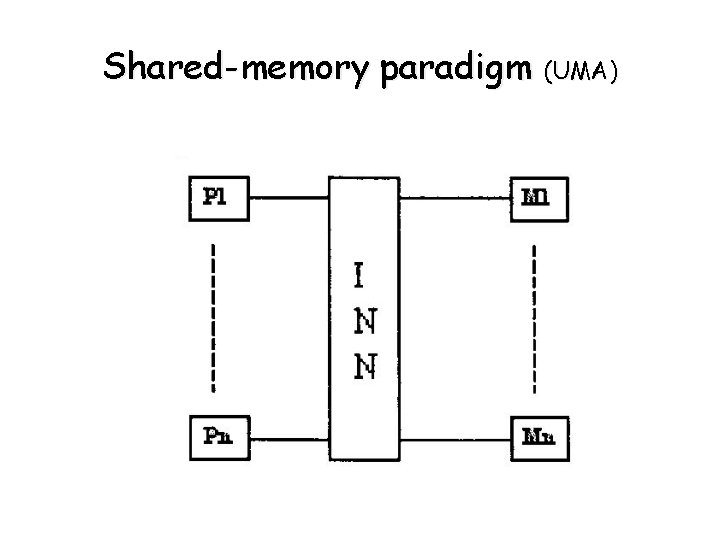
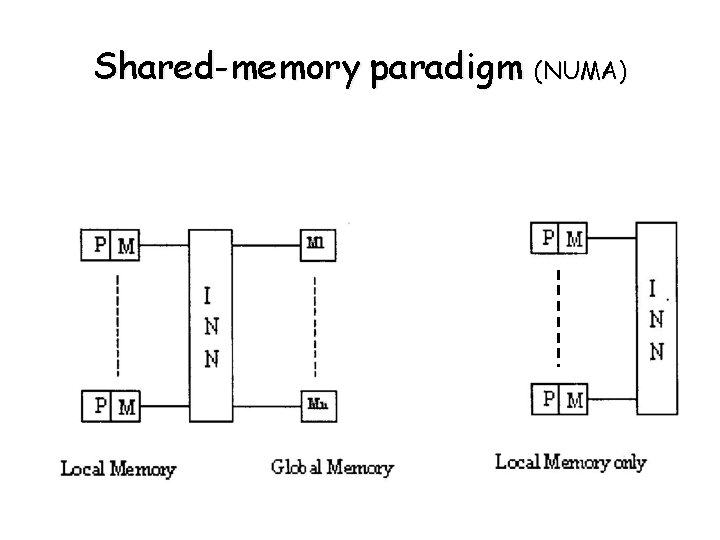
Address –Space organization • Two paradigms - Message passing - Shared-memory • Message Passing - pairs of PE and memory modules communicate between each other • Shared Address Space - each PE has access to any location in memory.

Message passing paradigm

Shared-memory paradigm (UMA)

Shared-memory paradigm (NUMA)

Interconnection Networks • Static (direct) – for message passing • Dynamic(indirect) - for shared-memory

Processor Granularity • Coarse–grain - for algorithms that require frequent communication • Medium-grain - for algorithms in which the ratio of the time required for basic communication to the time required for basic computation is small • Fine–grain - required frequent communication.

PRAM model (idealized parallel computer) • P is the number of processors - share common clock each works on its own instruction • M is the global memory - uniformly accessible to all PES • Synchronous shared memory MIMD computers • Interaction between PEs occurs at no cost

PRAM model (continued) • Depending on how memory is accessed for READ and WRITE operations following four subclasses: - EREW (exclusive read, exclusive write) - weakest, minimum concurrency - ERCW (excusive read, concurrent write) - CREW (concurrent read, exclusive write) - read access is concurrent, write access serialized - CRCW (concurrent read, concurrent write) - most powerful, can be simulated on a EREW model

PRAM model (continued) • CR (concurrent read) – does not need. Modification in program • CW (concurrent write) - access to memory requires arbitration • Protocols for CR - Common - iff all values are identical - Arbitrary – an arbitrary PE proceeds, other PEs fail - Priority – PE with highest priority wins - Sum – sum of all quantities is written

Dynamic Interconnection Networks • EREW PRAM - p processors - m words in global memory - switching elements (determine the memory word accessed) • Each P can access any of the memory words • Number of switching elements required UMA. • Very expensive (-) • Very good performance (+) (mp) for

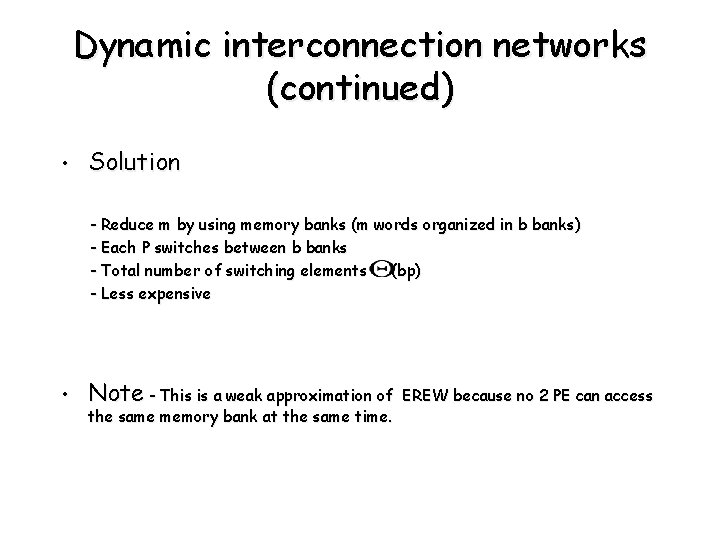
Dynamic interconnection networks (continued) • Solution - Reduce m by using memory banks (m words organized in b banks) - Each P switches between b banks - Total number of switching elements (bp) - Less expensive • Note - This is a weak approximation of the same memory bank at the same time. EREW because no 2 PE can access

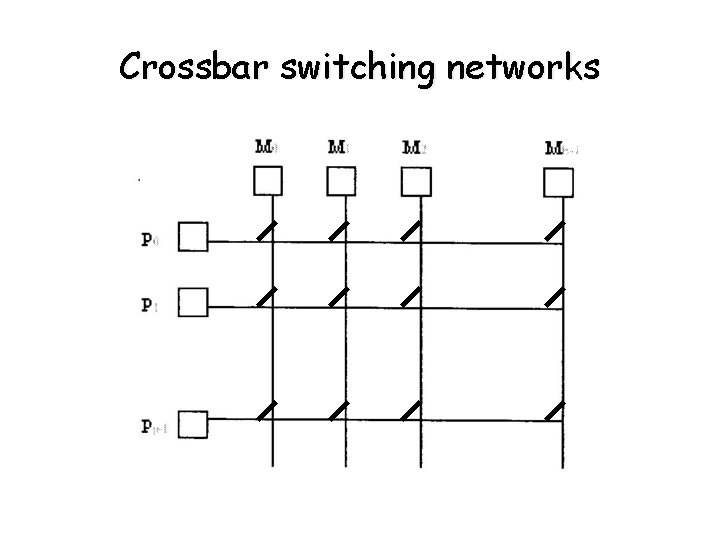
Crossbar switching networks

Crossbar switching networks (continued) • From the previous slide - p processors are connected to b memory banks by a crossbar switch. - each PE accesses one memory bank - m words are stored in the memory banks - if m = b, crossbar simulates EREW PRAM • Total number of switching elements • If p is very large and p > b (pb) - total number of switching elements grows as (p 2) - and more P are unable to access any memory bank - not scalable

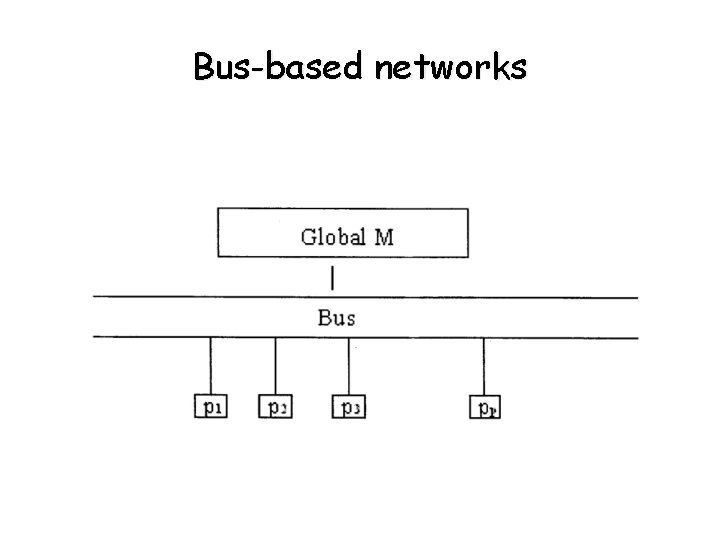
Bus-based networks

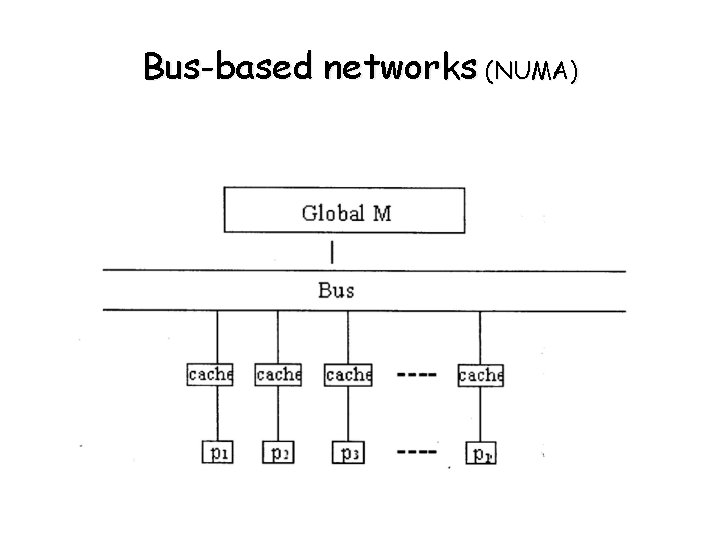
Bus-based networks (continued) • UMA - each PE accesses data from M over the same bus (UMA) - as p becomes very large, each PE spends an increasing amount of time waiting for memory access while the bus is used by other PEs. - not acceptable. • Solution (NUMA) - provide local-cache to reduce total number of accesses to global memory - this implies replicating data - cache coherency problems. - the architecture is shown on the following slide

Bus-based networks (NUMA)

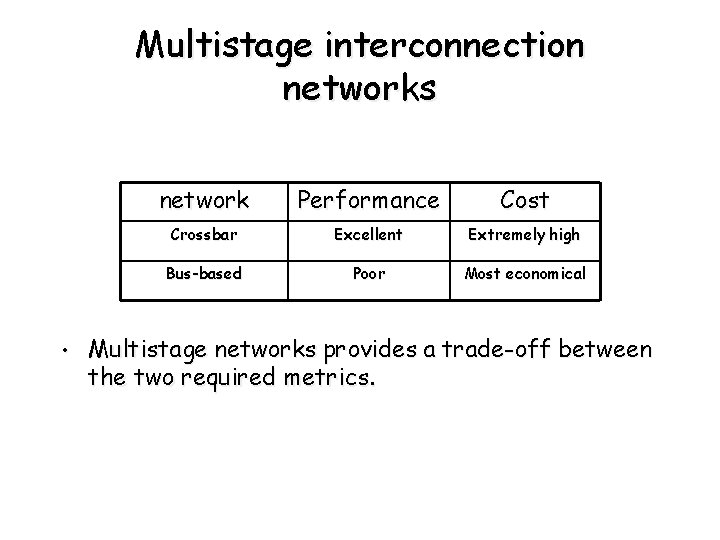
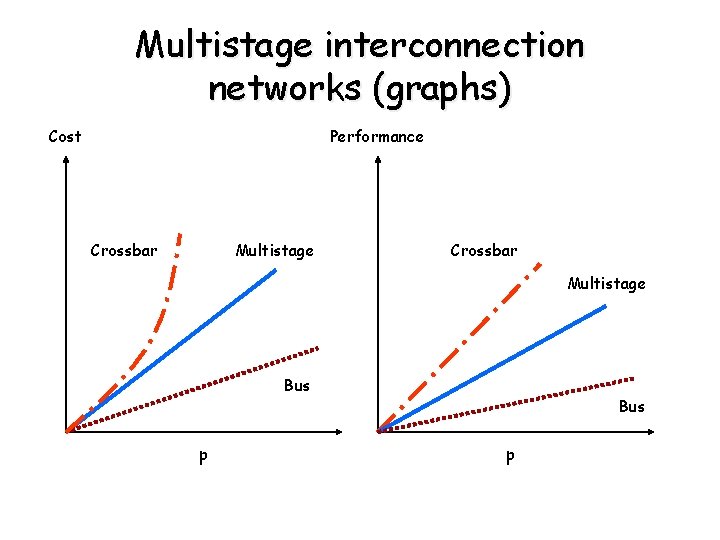
Multistage interconnection networks • network Performance Cost Crossbar Excellent Extremely high Bus-based Poor Most economical Multistage networks provides a trade-off between the two required metrics.

Multistage interconnection networks (graphs) Cost Performance Crossbar Multistage Bus p

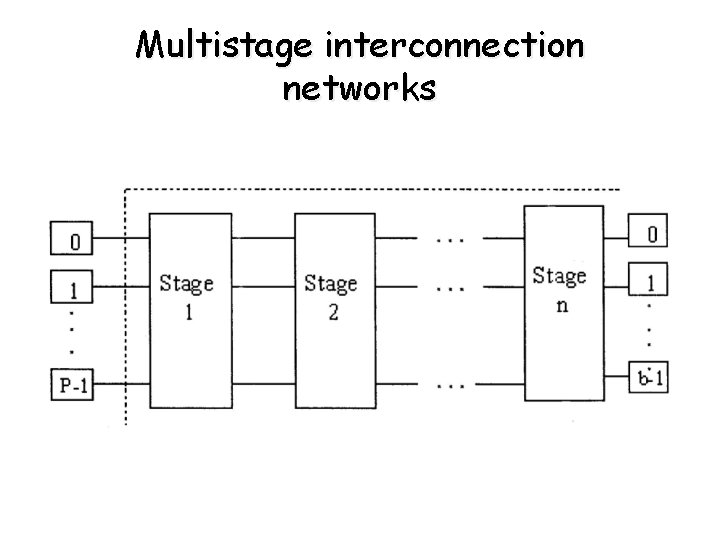
Multistage interconnection networks

Multistage interconnection networks (continued) • • • Cost is less than the Crossbar networks Performance better than the Bus-based networks Omega network - p is the # of PEs - b is the # memory banks - number of stages is log 2 p - p= b - a link exists between input i and output j if: j=

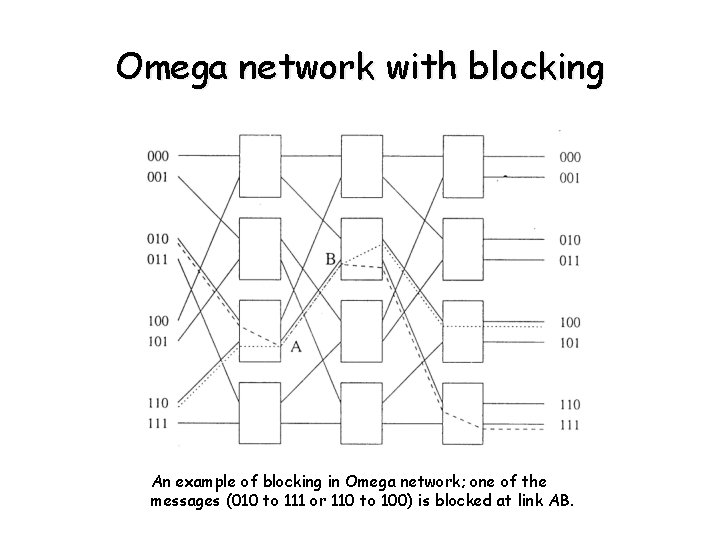
Omega network with blocking An example of blocking in Omega network; one of the messages (010 to 111 or 110 to 100) is blocked at link AB.

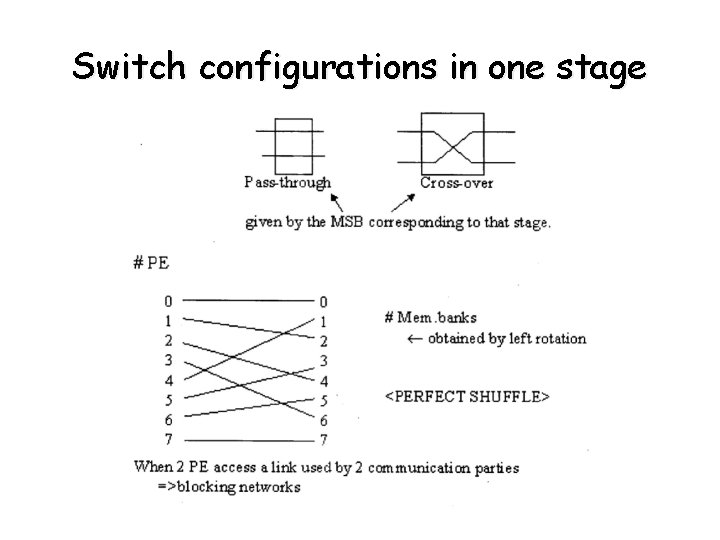
Switch configurations in one stage

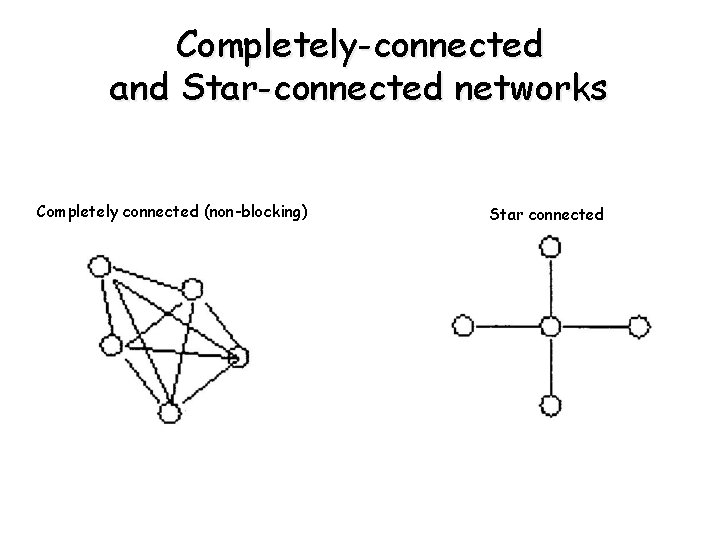
Static interconnection networks • Used in message passing • Completely-connected network • Star-connected network • Examples are shown on the following slide - similar to Crossbar but can support multiple channels - every PE connected to every other PE - communication takes place in 1 step - central PE (bottleneck) - similar to bus-based - communication takes place in 2 steps

Completely-connected and Star-connected networks Completely connected (non-blocking) Star connected

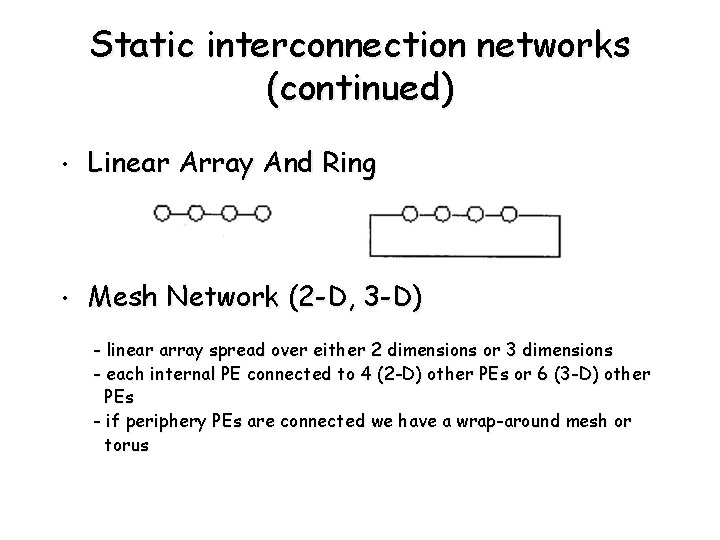
Static interconnection networks (continued) • Linear Array And Ring • Mesh Network (2 -D, 3 -D) - linear array spread over either 2 dimensions or 3 dimensions - each internal PE connected to 4 (2 -D) other PEs or 6 (3 -D) other PEs - if periphery PEs are connected we have a wrap-around mesh or torus

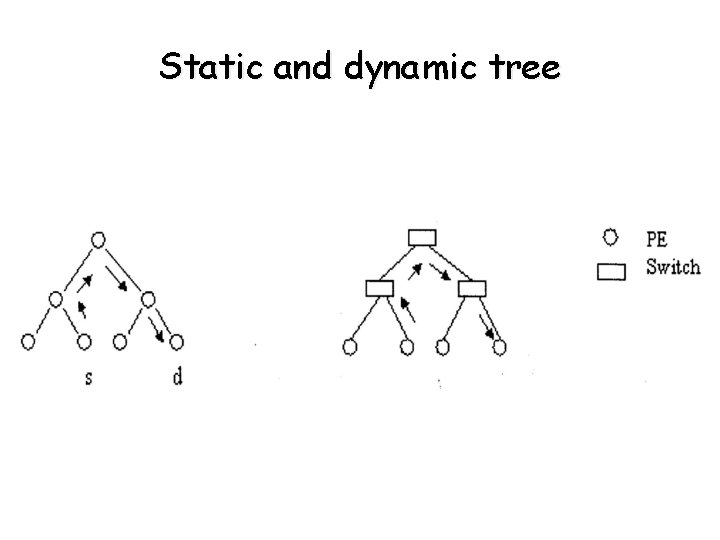
Tree networks • Only 1 path between any pair of PEs • Linear arrays and star- connected networks are special cases of tree nets • Static • Dynamic - each made corresponds to a PE - only leaf nodes are PEs - intermediate nodes are switching elements Examples of tree networks are shown on the following slides

Static and dynamic tree

Tree networks (continued) • Fat tree - increasing the number of communication links for PEs closer to the root. - in this way bottlenecks at higher levels in the tree are alleviated.

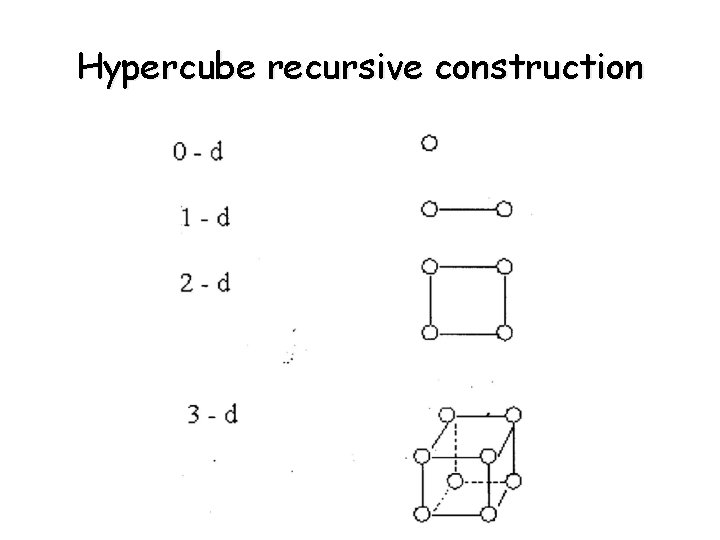
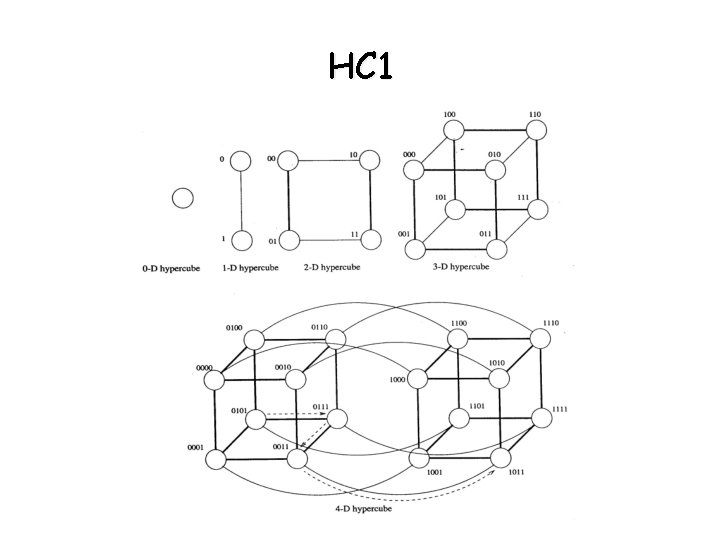
Hypercube networks • Multidimensional mesh with 2 PEs in each of the dimensions • A d-dimensional hypercube has p=2 d PEs • Can be constructed recursively - A (d+1)–dimensional hypercube is constructed by connecting the corresponding PEs of 2 separate d- dimensional hypercubes. - The labels of the PEs of one hypercube are prefixed with 0 and of the labels of the second hypercube with 1 - This is shown on the following slide

Hypercube recursive construction

HC 1

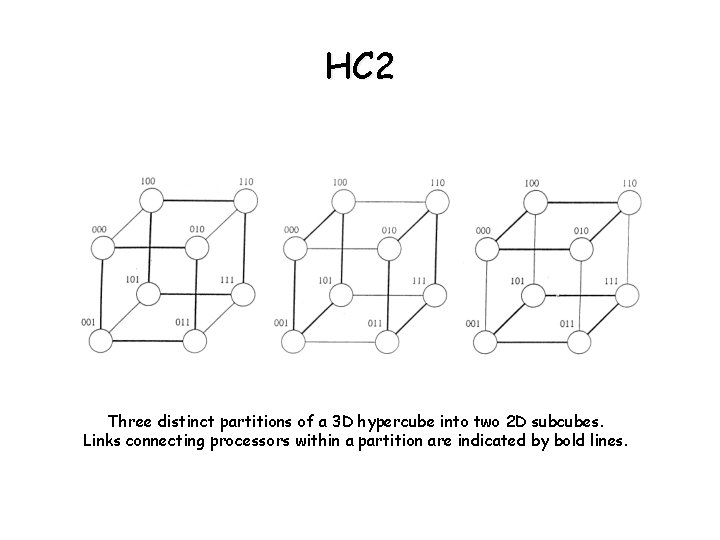
HC 2 Three distinct partitions of a 3 D hypercube into two 2 D subcubes. Links connecting processors within a partition are indicated by bold lines.

HC 3

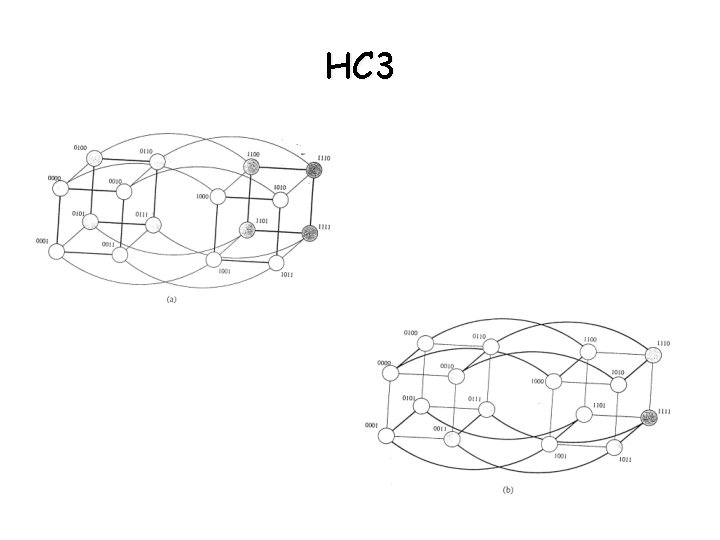
Hypercube properties • 2 PEs are connected by a direct link iff the binary representation of their labels differ at exactly one bit position. • In a d–dimensional Hy. C, each PE is directly connected to d other PEs • A d-dimensional Hy. C can be partitioned into 2 (d-1)- dimensional subcubes (see figure HC 2). Since PEs labels have d bits, d such partitions exist • Fixing any k-bits in a d-dimensional Hy. C with d-bits => PEs that differ in the remaining (d-k) bit positions form a (d-k)-dimensional subcube composed of 2 d-k 2 PEs (2 k such subcubes) see (fig HC 3) • Example: K=2, d=4 - 4 subcubes by fixing 2 MSB - 4 subcubes by fixing 2 LSB - always 4 subcubes formed by fixing any 2 bits

Hypercube properties (continued) • The total of bit positions at which 2 labels differ is the HAMMING distance between the 2 PEs - s is the source, t is the destination - s t is the Hamming distance • The number of communication links in the shortest path between 2 PEs is the Hamming distance between their labels. • The shortest path between any 2 PEs in a Hy. C cannot have more than d links (since s t cannot contain more than d bits)

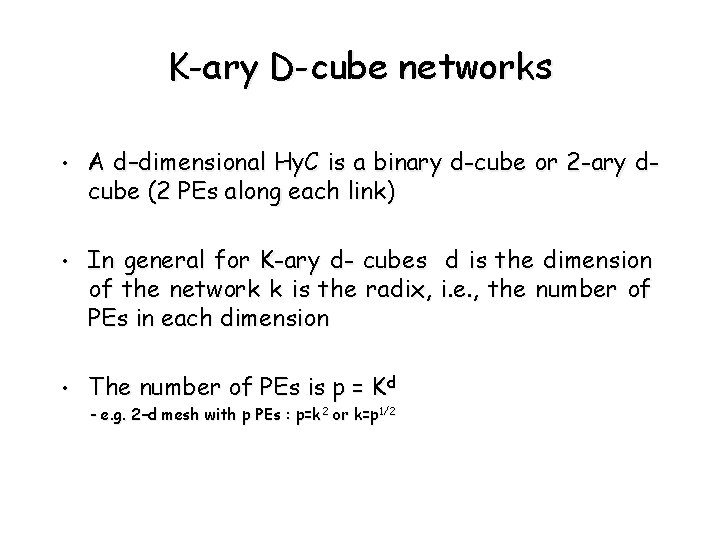
K-ary D-cube networks • A d–dimensional Hy. C is a binary d-cube or 2 -ary dcube (2 PEs along each link) • In general for K-ary d- cubes d is the dimension of the network k is the radix, i. e. , the number of PEs in each dimension • The number of PEs is p = Kd - e. g. 2–d mesh with p PEs : p=k 2 or k=p 1/2

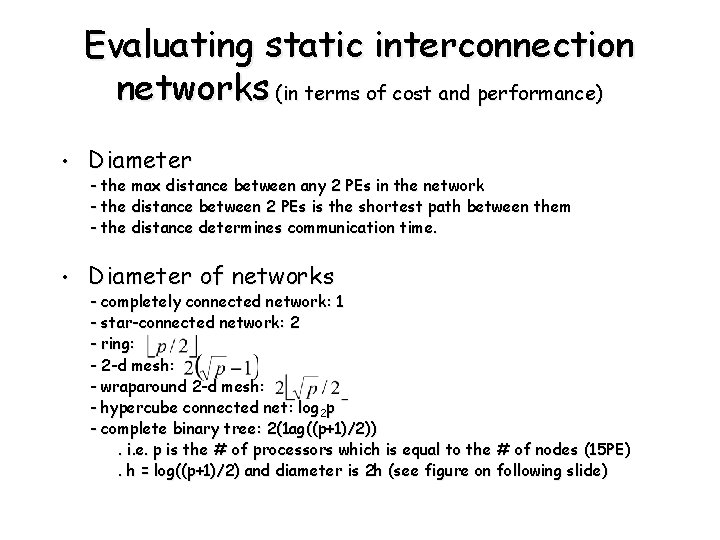
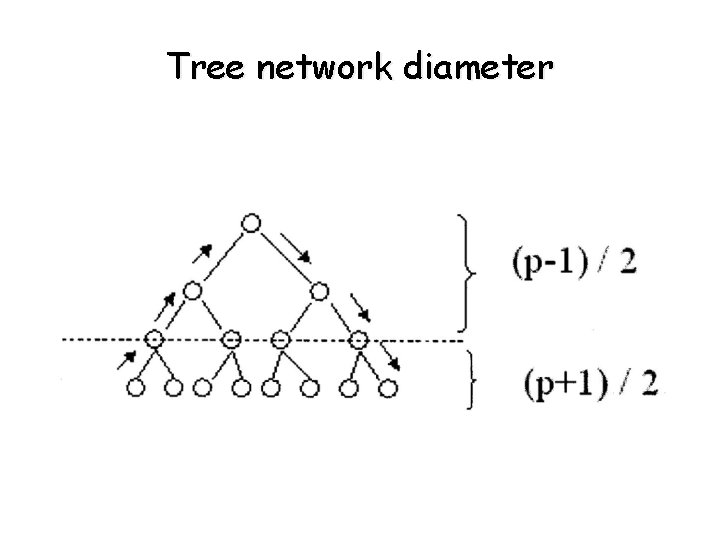
Evaluating static interconnection networks (in terms of cost and performance) • Diameter of networks - the max distance between any 2 PEs in the network - the distance between 2 PEs is the shortest path between them - the distance determines communication time. - completely connected network: 1 - star-connected network: 2 - ring: - 2 -d mesh: - wraparound 2 -d mesh: - hypercube connected net: log 2 p - complete binary tree: 2(1 ag((p+1)/2)). i. e. p is the # of processors which is equal to the # of nodes (15 PE). h = log((p+1)/2) and diameter is 2 h (see figure on following slide)

Tree network diameter

Evaluating static interconnection networks (continued) • Connectivity • High connectivity • Arc connectivity of networks - is a measure of the multiplicity of paths between 2 PEs – lower contention for communication resources - is a measure of connectivity - the minimum number of arcs that must be removed to break the network into 2 disconnected networks - linear arrays, star, tree: 1 - rings, 2 D mesh without wraparound: 2: - 2 D mesh with wraparound: 4 - d-dimensional hypercube: d

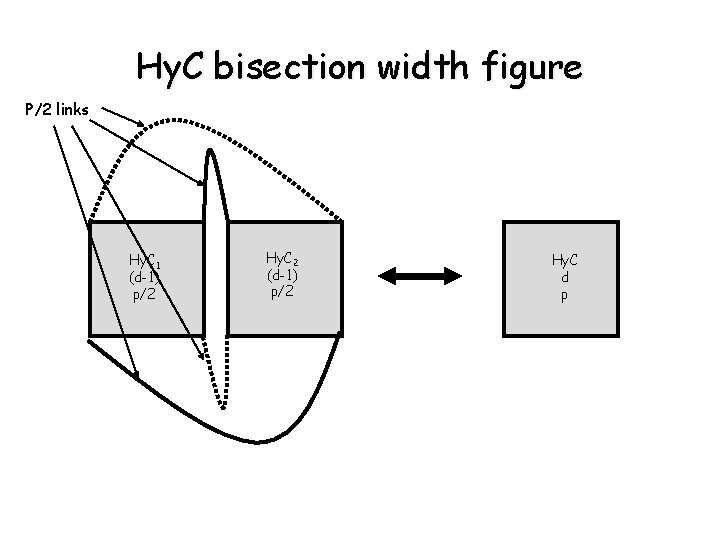
Bisection Width • The minimum number of communication links that have to be removed to partition the network into two equal halves. • Bisection width of networks - Ring: 2 - 2 D mesh w/0 wraparounds: p - 2 D mesh w/ wraparounds: 2 p - Tree , star: 1 (BWstar is the same as the Bwtree which is 1, since the star is special case of tree) - Fully-connected network: p 2/4 - Hypercube: p/2. i. e. d-dimensional Hy. C (p processors) consists of 2 X (d-1)–dimensional Hy. Cs (2 X P/2 processors). connect corresponding links to P/2 links

Hy. C bisection width figure P/2 links Hy. C 1 (d-1) p/2 Hy. C 2 (d-1) p/2 Hy. C d p

Bisection bandwidth • Channel width - The number of bits that can be simultaneously communicated over a link connecting 2 PEs (# of wires) • Channel rate - peak rate • Channel bandwidth (channel rate X channel width) - the peak rate at which data can be communicated between the ends of a communicated link • Bisection Bandwidth (bisection width x channel bandwidth) - minimum volume of communication allowed between any 2 halves of a network with an equal number of PEs

Cost • • Measured in terms of (a) number of communication links and (b) bisection bandwidth Number of communication links (number of wires required) - linear arrays, trees: p-1 (links) - d-dimensional mesh with wraparound: dp - Hy. C: (p/2) log 2 p • Bisection bandwidth - measures cost by providing a lower bound on the area (2 D) or the volume (3 D) of the packaging - if the bisection width of a networks is w. the lower bond an the area in 2 D is (w 2). lower bond an volume in 3 D is (w 3/2)

Embedding other networks into a hypercube • Given 2 graphs : G(V, E) and G(V’, E’), embedding graph G into graph G’ maps each vertex in the set V onto a vertex (or a set of vertices) in set V’ and each edge in set E onto an edge (or a set of edges) in E’ - nodes correspond to PEs and edges corresponds to communication links. • Why do we need Embedding? - Answer: It may be necessary to adapt one network to another (when an application is written for a specific network. Which is not available at present) • Parameters - congestion (# of edges in E mapped to one edge in E’) - dilation (reverse of congestion) - expansion (ratio of # vertices in V’ corresponding to one vertex in V) - contraction (reverse of expansion)

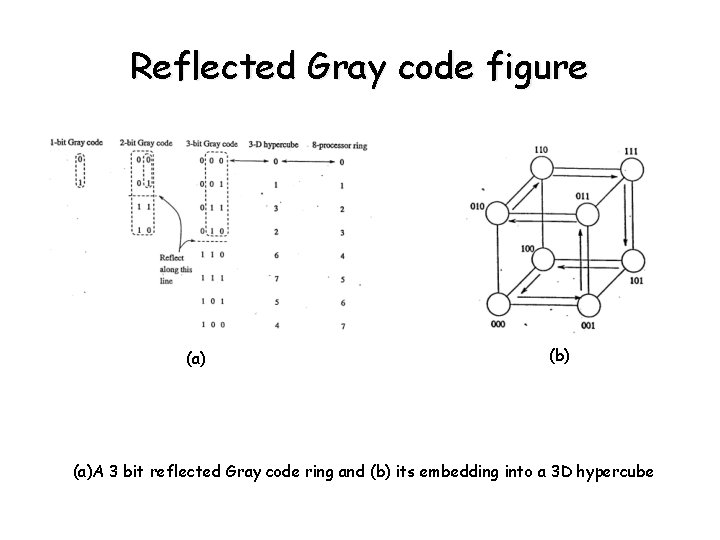
Embedding a linear array into a Hy. C • Linear array of 2 d processors (labeled 0… 2 d-1) can be embedded into a d-dimensional Hy. C by mapping processors i of the linear array to the processor with label G(i, d) of a Hy. C - G(0, 1)= 0 - G(1, 1)= 1 - G(i, x+1) = - The function G is the Binary Reflected Gray Code (RGC)

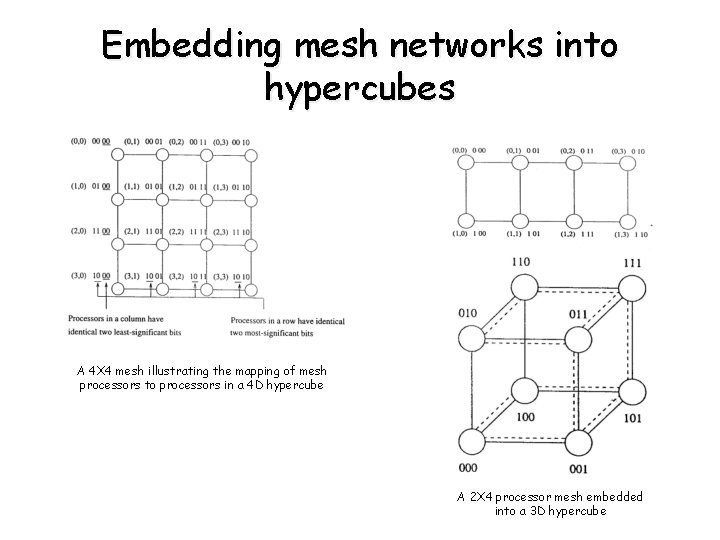
Embedding a Mesh into a Hypercube • Processors - in the same column have identical LSB - in the same row have identical MSB • Each row in the mesh is mapped to a unique subcube • Each column in the mesh is mapped to a unique subcube

Embedding mesh networks into hypercubes A 4 X 4 mesh illustrating the mapping of mesh processors to processors in a 4 D hypercube A 2 X 4 processor mesh embedded into a 3 D hypercube

Reflected Gray code figure (a) (b) (a)A 3 bit reflected Gray code ring and (b) its embedding into a 3 D hypercube

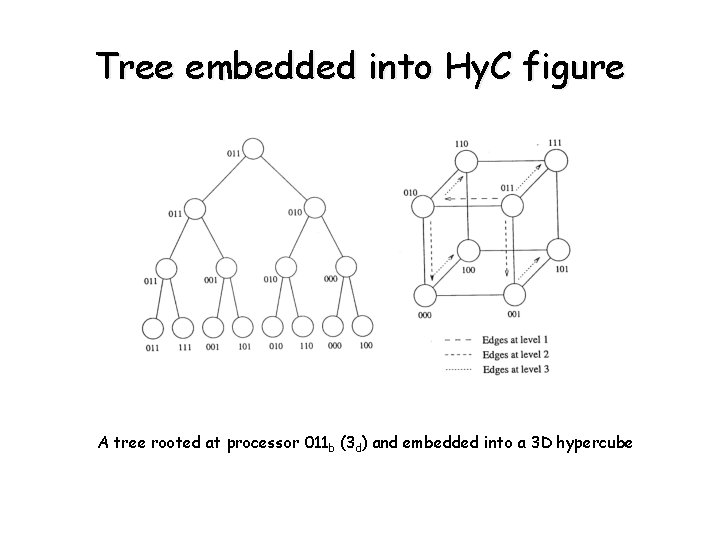
Embedding a binary tree into a hypercube • A Tree of depth d embedded in a 2 D PE Hy. C - The root of the tree is mapped auto a Hy. C processor - For each node m at depth j in the tree the left child of m is mapped to the Hy. C PE where m itself is mapped, and the right child of m is mapped to the Hy. C processor whose label we obtain by inverting bit j of i. . expansion = 1 (but max 4 nodes in tree may correspond to 1 node in Hy. C). congestion =. dilation = • Note: For array and mesh. expansion =. congestion =. dilation =

Tree embedded into Hy. C figure A tree rooted at processor 011 b (3 d) and embedded into a 3 D hypercube

Routing mechanisms for static networks • Routing mechanisms - determines the path a message takes through the network to get from the source to the destination processor. - considers. source. destination. into about state of net - returns one or more path(s)

Routing mechanisms for static networks (continued) • Classification (criteria) - congestion . minimal (shortest path between source and destination) - does not take congestion into consideration. non-minimal (avoids network congestion) - path may not be shortest - use of state of network information. deterministic routing( does not use network information) - determines a unique path - uses only source and destination information. Adaptive (uses network state information to avoid congestion)

Routing mechanisms for static networks (continued) • Dimension ordered routing (deterministic minimal) - XY– routing - E–Cube routing • X-Y routing - message sent along X dimension until it reaches the column of the destination PE, and then the message travels along Y dimension until it reaches its destination. The path length is |S x– Dx| + |Sy – Dy|

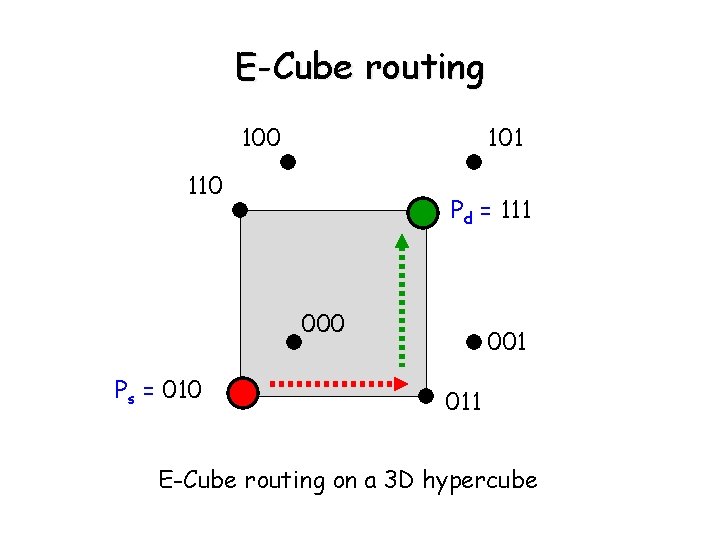
Routing mechanisms for static networks (continued) • E-cube routing -The minimum distance between 2 PE; Ps and Pd is given by the number of ones in the Ps Pd - Ps computes Ps Pd and sends a message along dimension K, where K is the position of the non-zero LSB in P s Pd. - At each intermediate step, Pi (the receiving PE) computes Pi Pd and forwards the message along the dimension corresponding to the non-zero LSB. - Process continues until destination is reached.

E-Cube routing 100 101 110 Pd = 111 000 Ps = 010 001 011 E-Cube routing on a 3 D hypercube

E-Cube routing on hypercube network • Ps = 010 and Pd = 111 • Step 1: Ps Pd is 010 111 = 101. - Ps forwards the message along the dimension corresponding to the LSB. 010 011 • Pi = 011 and Pd = 111 • Step 2: Pi Pd is 011 111 = 100. - Pi forwards message along the dimension corresponds to the non-zero LSB. 011 111.

Communication costs in static interconnection networks • Communication latency: • Parameters: • Influenced by: Time taken to communicate a message between two processors in the network. - Startup time – prepare message (add header, trailer, error correction information), execute routing algorithm, establish interface between PE and router. - Per-hop time (node latency) – time taken by the header to travel between two directly connected PEs. - Per word transfer time – if channel bandwidth is r words/sec, each transfer takes tw = 1/r seconds to traverse the link. - network topology - switching techniques.

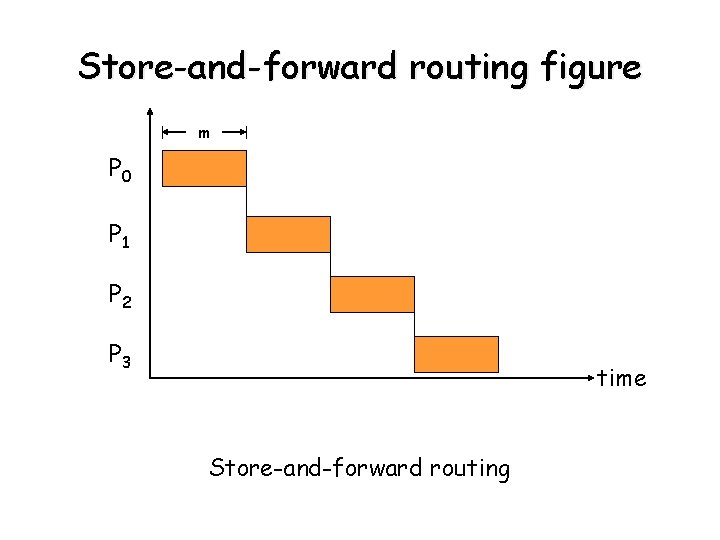
Store-and-forward routing • Each intermediate processor on the path forwards the message to the next processor after it has received and stored the entire message. m, message size. l, number of links to traverse. th, cost of header traversing the link. tw, per-word message transfer time. mtw, cost of the rest of the message traversing the link. Then communication cost is, tcomm = ts + (th + mtw)l Since th is small compared to mtw, we have tcomm = ts + mt wl. ts and tw are constants, therefore tcomm = (ml).

Store-and-forward routing figure m P 0 P 1 P 2 P 3 time Store-and-forward routing

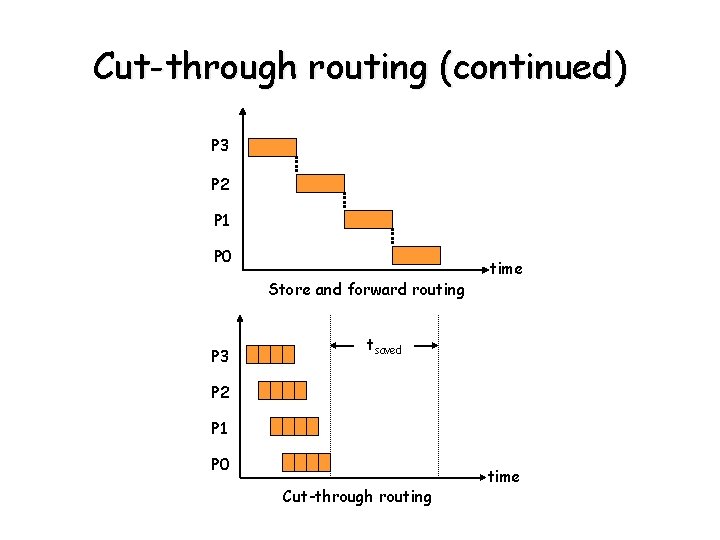
Cut-through routing • Store-and-forward routing disadvantages: • Cut-through routing: • Notes: - communication time is high. - poor utilization of communication resources. - message is forwarded from the incoming link to the outgoing link as it arrives. - message travels in small units called flow control digits or flits (pipelined through the network). - an intermediate processor does not wait for the entire message to arrive before forwarding. As soon as the flits arrive they are passed on to the next processor. - all flits are routed along the same path. - no need for buffer space to store entire message at intermediate PEs. - uses less memory storage and memory bandwidth. - it is faster.

Cut-through routing (continued) • Notes: - no need for buffer space to store entire message at intermediate PEs. - uses less memory storage and memory bandwidth. - it is faster. (incomplete) • From the figures on the next slide tcomm = (ts + thl+ mtw) < (ts + l(th + mtw)) = t. SF if ts = constant, then tcomm = (m+l) if l = 1, then tcomm(CT) = tcomm(SF) : (m)

Cut-through routing (continued) P 3 P 2 P 1 P 0 Store and forward routing P 3 time tsaved P 2 P 1 P 0 Cut-through routing time

Cost-performance trade offs • Performance analysis of a mesh and Hy. C with identical costs (based on various cost metrics) • Cost of network is proportional to - number of wires - bisection width • Assumption: lightly loaded networks and cut through routing

Cost-performance trade offs (continued) 1. If cost of network is proportional to the number of wires - 2 D wraparound mesh with (logp/4) wires per channel costs as much as a p-processor Hy. C with 1 wire per channel. (see page 38, table 2. 1) - Average communication latencies (for mesh and Hy. C of the same cost). lav, average distance between 2 PE - p/2, in 2 D wraparound mesh - log p/2 in Hy. C. time to send a message of size m between PEs that are l av hops apart is given by ts + th lav + tw m, for cut–through routing

Cost-performance trade offs (continued) • In mesh - channel width scaled up by (logp)/4 - per word transfer time reduced by (logp)/4 • In Hy. C - if per-word transfer time is tw, the same time for mesh is: 4 tw/log P, that is, tw(mesh) = (4/logp)tw(Hy. C) • Average communication latency - Hy. C, ts + th(logp/2) + twm - Mesh, ts + th( p/2) + 4 mtw/logp

Cost-performance trade offs (continued) • Analysis p = constant and m is large, communication due to t w dominates 4 mtw/log p (mesh) < twm (Hy. C), if p > 16 • Paint-to-point communication of large messages between random pairs of PE takes less times on a wraparound mesh with cut-through routing, than on a Hy. C of the same cost • Note – if stare-and–forward routing is used, the mesh is not more cost efficient than Hy. C - the above analysis was performed under light load conditions in the network - if the number of messages is large, contention increase and mesh is affected by contention more than Hy. C - for heavy load conditions Hy. C is better than mesh

Cost-performance trade offs (continued) 2. If cost of network is proportional to its bisection width - 2 D wraparound mesh (p processors) with p/4 wires per channel has a cost equal to a p processor Hy. C with 1 wire per channel (see page 38, table 2. 1) • Average communication latencies (for mesh and Hy. C of same cost) - Mesh channels wider by p/4 which means that per word transfer time is reduced by the same factor of p/4 - communication latencies for Hy. C and mesh. HC, ts + th(log p)/2 + twm. Mesh, ts + th p/2 + (4 mtw)(1/ p)

Cost-performance trade offs (continued) • Analysis - p = constant and m is large, t w dominates for p > 16 - mesh outperforms Hy. C of the same cost, provided the network is lightly loaded. - for heavily loaded networks Perf mesh Perf. Hy. C