Introduction to Algorithms Rabie A Ramadan rabierabieramadan org

Introduction to Algorithms Rabie A. Ramadan rabie@rabieramadan. org http: //www. rabieramadan. org 3 Some of the sides are exported from different sources to clarify the topic

Time efficiency of nonrecursive algorithms General Plan for Analysis l Decide on parameter n indicating input size l Identify algorithm’s basic operation l Determine worst, average, and best cases for input of size n l Set up a sum for the number of times the basic operation is executed l Simplify the sum using standard formulas and rules.

Example 1: The Largest Element T(n) = 1 i n-1 (1) = n-1 = (n) comparisons

Example 2: Element uniqueness problem T(n) = 0 i n-2 ( i+1 j n-1 (1)) ( = 0 i n-2 (n-i+1) = = ( ) comparisons

Example 3: Matrix multiplication T(n) = = ( Ignored addition for simplicity ) multiplications

Example 4: Counting binary digits It cannot be investigated the way the previous examples are. The halving game: Find integer i such that n/ Answer: i ≤ log n. ≤ 1. So, T(n) = (log n) divisions. Another solution: Using recurrence relations.

Plan for Analysis of Recursive Algorithms l Decide on a parameter indicating an input’s size. l Identify the algorithm’s basic operation. l Check whether the number of times the basic op. is executed may vary on different inputs of the same size. (If it may, the worst, average, and best cases must be investigated separately. ) l Set up a recurrence relation with an appropriate initial condition expressing the number of times the basic op. is executed. l Solve the recurrence (or, at the very least, establish its solution’s order of growth) by backward substitutions or another method.

Example 1 : Factorial: Recursive Algorithm The stopping condition is n=0 A repetitive algorithm uses recursion whenever the algorithm appears within the definition itself. 8

Example 1: Recursive evaluation of n! Definition: n ! = 1 2 … (n-1) n for n ≥ 1 and 0! = 1 Recursive definition of n!: F(n) = F(n-1) n for n ≥ 1 and F(0) = 1 Size: Basic operation: Recurrence relation: n multiplication M(n) = M(n-1) (for F(n-1) ) + 1 (for the n * F(n-1)) M(0) = 0
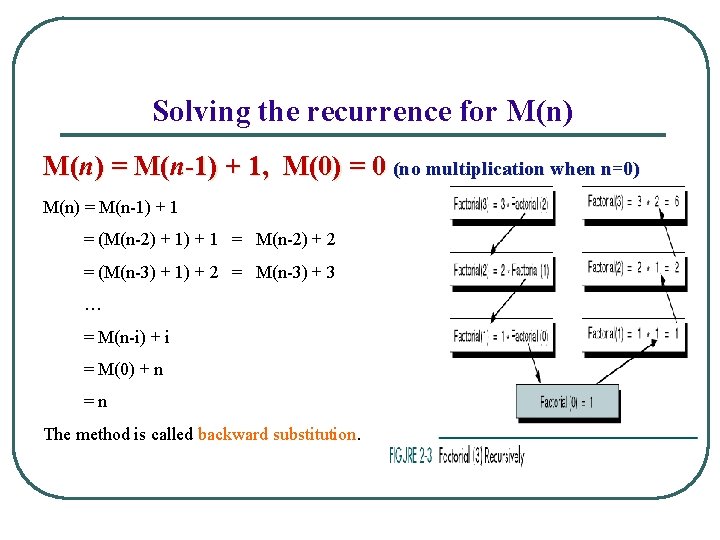
Solving the recurrence for M(n) = M(n-1) + 1, M(0) = 0 (no multiplication when n=0) M(n) = M(n-1) + 1 = (M(n-2) + 1 = M(n-2) + 2 = (M(n-3) + 1) + 2 = M(n-3) + 3 … = M(n-i) + i = M(0) + n =n The method is called backward substitution.

Example 2: The Tower of Hanoi Puzzle Towers of Hanoi (aka Tower of Hanoi) is a mathematical puzzle invented by a French Mathematician Edouard Lucas in 1983. • Initially the game has few discs arranged in the increasing order of size in one of the tower. • The number of discs can vary, but there are only three towers. • The goal is to transfer the discs from one tower another tower. However you can move only one disk at a time and you can never place a bigger disc over a smaller disk. It is also understood that you can only take the top most disc from any given tower. 11
Example 2: The Tower of Hanoi Puzzle Recurrence for number of moves: M(n) = 2 M(n-1) + 1
0 1 2 3 4 5 6 7 Move Sequence for d = 3

The Tower of Hanoi Puzzle l l l l Here's how to find the number of moves needed to transfer larger numbers of disks from post A to post C, when M = the number of moves needed to transfer n-1 disks from post A to post C: for 1 disk it takes 1 move to transfer 1 disk from post A to post C; for 2 disks, it will take 3 moves: 2 M + 1 = 2(1) + 1 = 3 for 3 disks, it will take 7 moves: 2 M + 1 = 2(3) + 1 = 7 for 4 disks, it will take 15 moves: 2 M + 1 = 2(7) + 1 = 15 for 5 disks, it will take 31 moves: 2 M + 1 = 2(15) + 1 = 31 for 6 disks. . . ?
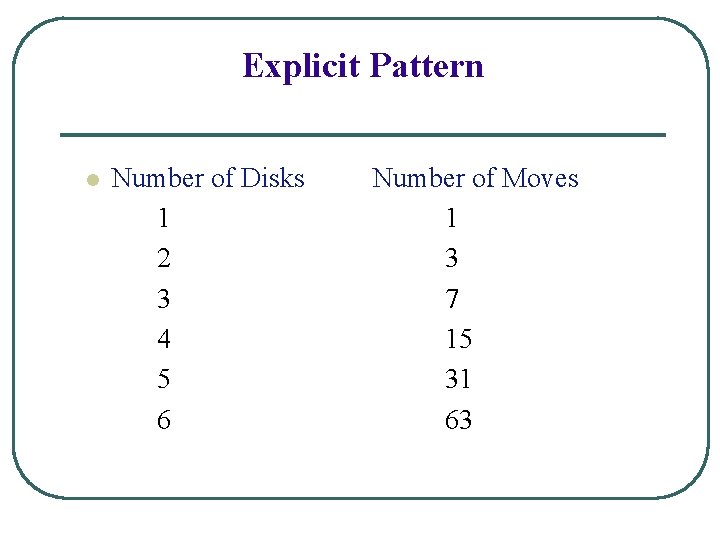
Explicit Pattern l Number of Disks 1 2 3 4 5 6 Number of Moves 1 3 7 15 31 63

Powers of two help reveal the pattern: l Number of Disks (n) 1 2 3 4 5 6 Number of Moves 21 - 1 = 2 - 1 = 1 22 - 1 = 4 - 1 = 3 23 - 1 = 8 - 1 = 7 24 - 1 = 16 - 1 = 15 25 - 1 = 32 - 1 = 31 26 - 1 = 64 - 1 = 63

Fascinating fact So the formula for finding the number of steps it takes to transfer n disks from post A to post C is: 2 n- 1

Solving recurrence for number of moves M(n) = 2 M(n-1) + 1, M(1) = 1 M(n) = 2 M(n-1) + 1 = 2(2 M(n-2) + 1 = 2^2*M(n-2) + 2^1 + 2^0 = 2^2*(2 M(n-3) + 1) + 2^1 + 2^0 = 2^3*M(n-3) + 2^2 + 2^1 + 2^0 =… = 2^(n-1)*M(1) + 2^(n-2) + … + 2^1 + 2^0 = 2^(n-1) + 2^(n-2) + … + 2^1 + 2^0 = 2^n -1

Fibonacci Sequence l The Fibonacci numbers: 0, 1, 1, 2, 3, 5, 8, 13, 21, … What Is the Important of Fibonacci Sequence? The Fibonacci recurrence: F(n) = F(n-1) + F(n-2) F(0) = 0 F(1) = 1 l F(n) = F(n-1) + F(n-2) or F(n) - F(n-1) - F(n-2) = 0 General 2 nd order linear homogeneous recurrence with constant coefficients: a. X(n) + b. X(n-1) + c. X(n-2) = 0 l

Chapter 3 Brute Force Copyright © 2007 Pearson Addison-Wesley. All rights reserved.

Brute Force A straightforward approach, usually based directly on the problem’s statement and definitions of the concepts involved Examples: 1. Computing an (a > 0, n a nonnegative integer)= a*a*…. *a 2. 3. 4. Computing n! Multiplying two matrices Searching for a key of a given value in a list

Brute-Force Sorting Algorithm Selection Sort Scan the array to find its smallest element and swap it with the first element. Then, starting with the second element, scan the elements to the right of it to find the smallest among them and swap it with the second elements. Generally, on pass i (0 i n-2), find the smallest element in A[i. . n-1] and swap it with A[i]: A[0] . . . A[i-1] | A[i], . . . , A[min], . . . , A[n-1] in their final positions Example: 7 3 2 5

Analysis of Selection Sort Time efficiency: Space efficiency: Stability: Θ(n^2) Θ(1), so in place yes

Brute Force - Bubble Sort Another brute force application to the sorting problem is to • compare adjacent elements of the list. • and exchange them if they are out of order. By doing it repeatedly, we end up “Bubbling up” the largest element to the last position on the list The next pass bubbles up the second largest element, and so on until, after n-1 passes, the list is sorted. 24
![Brute Force - Bubble Sort Algorithm Bubble. Sort (A[0…n-1]) for i ← 0 to Brute Force - Bubble Sort Algorithm Bubble. Sort (A[0…n-1]) for i ← 0 to](http://slidetodoc.com/presentation_image_h2/4dc039a836598b454a90d28990f31e2a/image-25.jpg)
Brute Force - Bubble Sort Algorithm Bubble. Sort (A[0…n-1]) for i ← 0 to n-2 do for j ← 0 to n-2 -i do if A[j]<A[j+1] swap A[j] and A[j+1] The number of times it is executed T(n) depends only on the array’s size and is given by the following sum: 25

Brute-Force String Matching l l l pattern: pattern a string of m characters to search for text: text a (longer) string of n characters to search in problem: problem find a substring in the text that matches the pattern Brute-force algorithm Step 1 Align pattern at beginning of text Step 2 Moving from left to right, compare each character of pattern to the corresponding character in text until • all characters are found to match (successful search); or • a mismatch is detected Step 3 While pattern is not found and the text is not yet exhausted, realign pattern one position to the right and repeat Step 2

Examples of Brute-Force String Matching 1. Pattern: 001011 Text: 1001010110100101111010 2. Pattern: happy Text: It is never too late to have a happy childhood.

Pseudocode and Efficiency Time efficiency: Θ(mn) comparisons (in the worst case) Why?

Brute-Force Polynomial Evaluation Problem: Find the value of polynomial p(x) = anxn + an-1 xn-1 +… + a 1 x 1 + a 0 at a point x = x 0 Brute-force algorithm p 0. 0 for i n downto 0 do power 1 for j 1 to i do //compute xi power x p p + a[i] power return p Efficiency: Θ(n^2) multiplications

Polynomial Evaluation: Improvement We can do better by evaluating from right to left: Better brute-force algorithm p a[0] power 1 for i 1 to n do power x p p + a[i] power return p Efficiency: Θ(n) multiplications Horner’s Rule is another linear time method.

Closest-Pair Problem Find the two closest points in a set of n points (in the two-dimensional Cartesian plane). Brute-force algorithm Compute the distance between every pair of distinct points and return the indexes of the points for which the distance is the smallest.

Closest-Pair Brute-Force Algorithm (cont. ) Efficiency: How to make it faster? Θ(n^2) multiplications Using divide-and-conquer!

Brute-Force Strengths and Weaknesses l Strengths • wide applicability • simplicity • yields reasonable algorithms for some important problems (e. g. , matrix multiplication, sorting, searching, string matching) l Weaknesses • rarely yields efficient algorithms • some brute-force algorithms are unacceptably slow • not as constructive as some other design techniques

Exhaustive Search A brute force solution to a problem involving search for an element with a special property, usually among combinatorial objects such as permutations, combinations, or subsets of a set. Method: Method • generate a list of all potential solutions to the problem in a systematic manner • evaluate potential solutions one by one, disqualifying infeasible ones and, for an optimization problem, keeping track of the best one found so far • when search ends, announce the solution(s) found

Example 1: Traveling Salesman Problem l l l Given n cities with known distances between each pair, find the shortest tour that passes through all the cities exactly once before returning to the starting city Alternatively: Find shortest Hamiltonian circuit in a weighted connected graph Example: Example 2 a 8 c b 5 3 7 4 d How do we represent a solution (Hamiltonian circuit)?
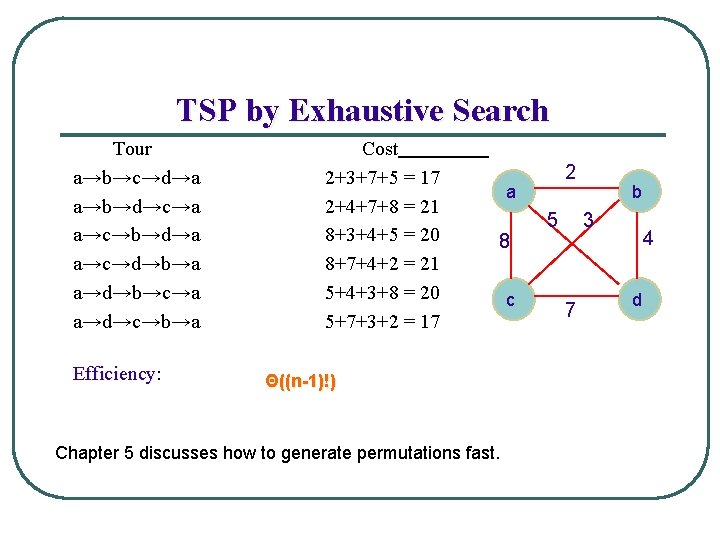
TSP by Exhaustive Search Tour a→b→c→d→a a→b→d→c→a a→c→b→d→a a→c→d→b→a a→d→b→c→a a→d→c→b→a Efficiency: Efficiency Cost 2+3+7+5 = 17 2+4+7+8 = 21 8+3+4+5 = 20 8+7+4+2 = 21 5+4+3+8 = 20 5+7+3+2 = 17 2 a 8 Θ((n-1)!) Chapter 5 discusses how to generate permutations fast. c 5 b 3 7 4 d

Example 2: Knapsack Problem Given n items: • weights: w 1 w 2 … wn • values: v 1 v 2 … vn • a knapsack of capacity W Find most valuable subset of the items that fit into the knapsack Example: Knapsack capacity W=16 item weight value 1 2 $20 2 5 $30 3 10 $50 4 5 $10
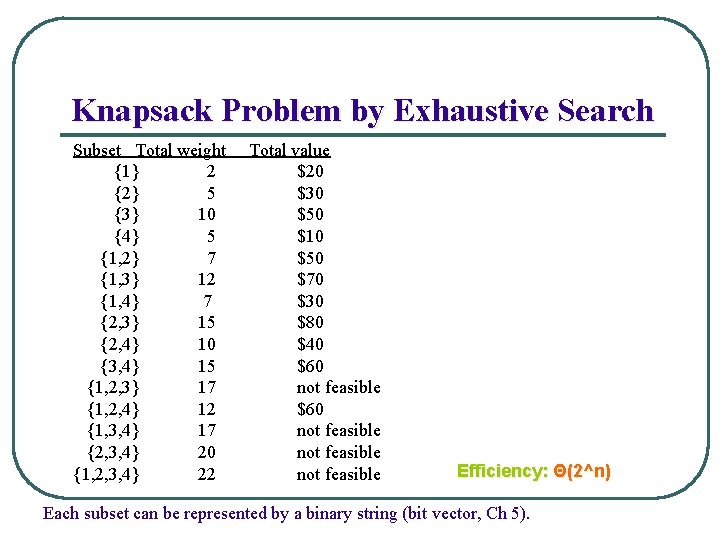
Knapsack Problem by Exhaustive Search Subset Total weight {1} 2 {2} 5 {3} 10 {4} 5 {1, 2} 7 {1, 3} 12 {1, 4} 7 {2, 3} 15 {2, 4} 10 {3, 4} 15 {1, 2, 3} 17 {1, 2, 4} 12 {1, 3, 4} 17 {2, 3, 4} 20 {1, 2, 3, 4} 22 Total value $20 $30 $50 $10 $50 $70 $30 $80 $40 $60 not feasible Efficiency: Θ(2^n) Each subset can be represented by a binary string (bit vector, Ch 5).

Example 3: The Assignment Problem There are n people who need to be assigned to n jobs, one person per job. The cost of assigning person i to job j is C[i, j]. Find an assignment that minimizes the total cost. Person 1 Person 2 Person 3 Person 4 Job 1 Job 2 Job 3 Job 4 9 2 7 8 6 4 3 7 5 8 1 8 7 6 9 4 Algorithmic Plan: Generate all legitimate assignments, compute their costs, and select the cheapest one. How many assignments are there? n!

Assignment Problem by Exhaustive Search C= 9 2 7 8 6 4 3 7 5 8 1 8 7 6 9 4 Assignment (col. #s) 1, 2, 3, 4 1, 2, 4, 3 1, 3, 2, 4 1, 3, 4, 2 1, 4, 2, 3 1, 4, 3, 2 Total Cost 9+4+1+4=18 9+4+8+9=30 9+3+8+4=24 9+3+8+6=26 9+7+8+9=33 9+7+1+6=23 etc. (For this particular instance, the optimal assignment can be found by exploiting the specific features of the number given. It is: 2, 1, 3, 4 )

Final Comments on Exhaustive Search l Exhaustive-search algorithms run in a realistic amount of time only on very small instances l In some cases, there are much better alternatives! • Euler circuits • shortest paths The Hungarian method runs • assignment problem in O(n^3) time. l In many cases, exhaustive search or its variation is the only known way to get exact solution
- Slides: 41