Introduction to Algorithms LECTURE 16 Chap 22 Elementary

Breadth First Search Breadth first search animation

Initialize 4 2 1 1 pred(1) =all Unmark 0 nodes in N; next :

Select a node i in LIST 4 2 1 1 In breadth first search,

If node i is incident to an admissible arc… 2 2 1 1 4

If node i is incident to an admissible arc… 2 2 4 1 1

If node i is not incident to an admissible arc… 2 2 4 1

Select Node i 2 2 4 1 1 5 3 The first node on

Select a node 2 2 4 1 1 5 The first node on LIST

Select node 3 2 2 4 1 1 5 node is not 3 delete

Select node 8 2 2 4 1 1 5 node 8 is not incident

Select node 7 2 2 4 1 1 5 node 7 is not incident

Select node 9 2 2 4 1 1 5 node 9 is not incident

Depth First Search Breadth first search animation

Select a node i in LIST 4 2 1 1 In depth first search,

Select the last node on LIST 2 2 1 1 1 8 5 3

Select 2 2 1 1 5 Select the last node on LIST 1 4

If node i is incident to an admissible arc… 2 2 4 3 1

Select 2 2 4 3 1 1 5 Select the last node on LIST

If node i is not incident to an admissible arc… 2 2 4 3

Select the last node on LIST 2 2 4 3 1 1 5 5

Select node 9 2 2 4 3 1 1 5 Delete But node 9

Select node 6 2 2 4 3 1 1 5 Delete But node 6

Select node 5 2 2 4 3 1 1 5 But node 5 is

Select node 4 2 2 4 3 1 1 5 Delete But node 4

Select node 2 2 2 4 3 1 1 5 Delete But node 2

Select node 1 2 2 4 3 1 1 5 Next : =Node Select

Select node 3 2 2 4 3 1 1 5 Delete But node 3

Select node 1 2 2 4 3 1 1 5 Delete But node 1

LIST is empty 2 2 4 3 1 1 5 The algorithm ends! LIST

The depth first search tree Note that each induced subtree has consecutively labeled nodes

Topological Ordering Breadth first search animation

Preliminary to Topological Sorting LEMMA. If each node has at least one arc going

Initialization “Next” Determine LIST is will thethe set be of indegree nodes label with

Select a node from LIST next Select : = next a +1 order(i) node

Select a node from LIST next : = next Select a +1 order(i) :

Select a node from LIST 3 6 next : = next Select a +1

Select a node from LIST 1 5 3 6 next : = next Select

Select a node from LIST 1 5 3 6 next : = next +1

Slides: 66

Download presentation

Introduction to Algorithms LECTURE 16 (Chap. 22) Elementary Graph Algorithm • 22. 2 Breath-first search • 22. 3 Depth-first search • 22. 4 Topological sort Breadth first search animation

Breadth First Search Breadth first search animation

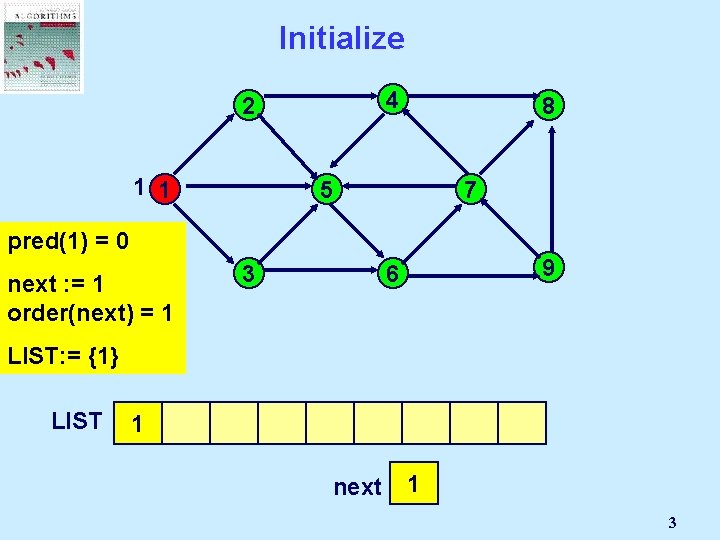
Initialize 4 2 1 1 pred(1) =all Unmark 0 nodes in N; next : = 1 Mark node s= 1 order(next) 8 5 3 7 9 6 LIST: = {1} LIST 1 next 1 3

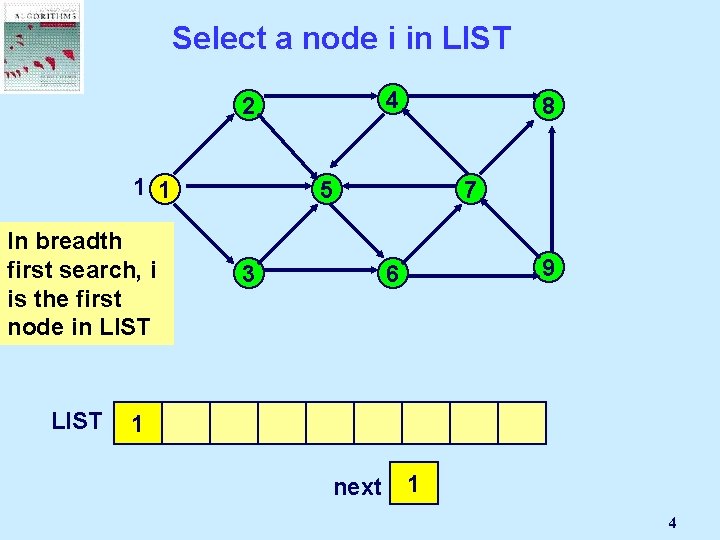
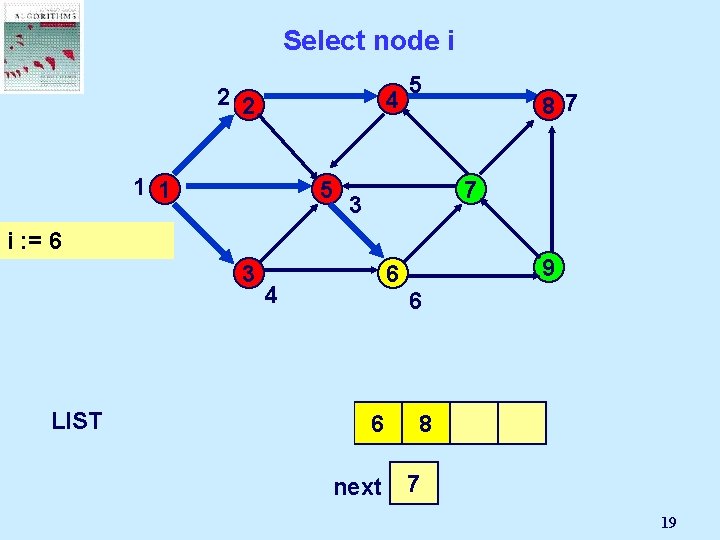
Select a node i in LIST 4 2 1 1 In breadth first search, i is the first node in LIST 8 5 3 7 9 6 1 next 1 4

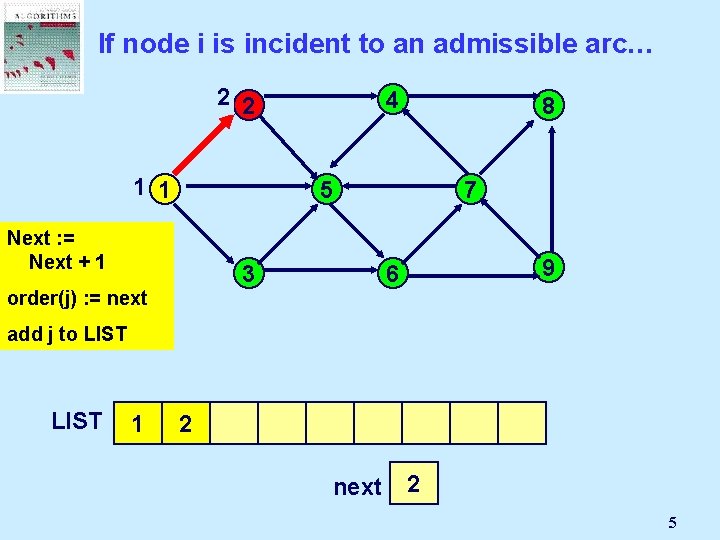
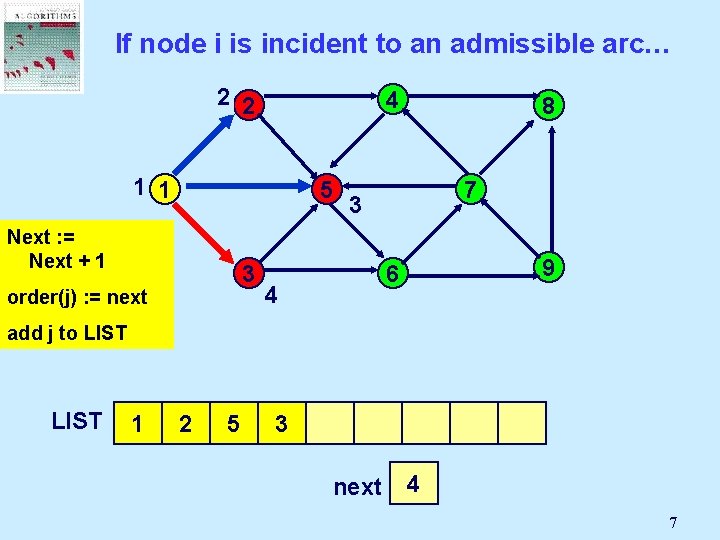
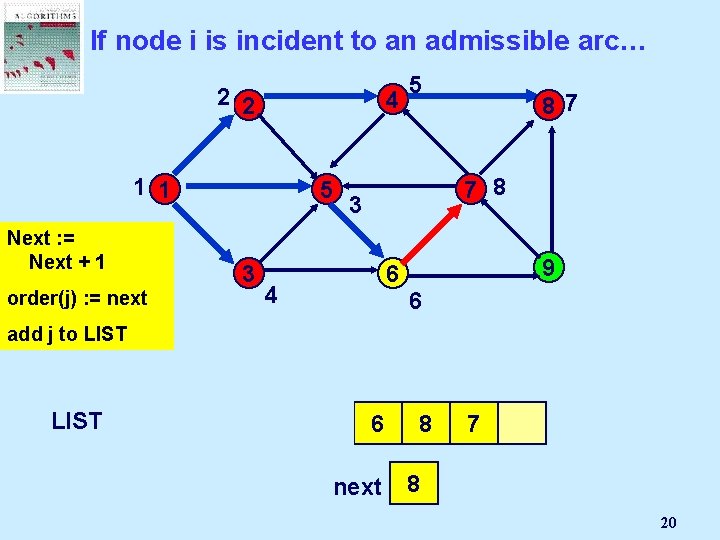
If node i is incident to an admissible arc… 2 2 1 1 4 8 5 Next : =Node Select Mark an j Next + 1 admissible 3 pred(j) : = i order(j) arc (i, j): = next 7 9 6 add j to LIST 1 2 next 2 1 5

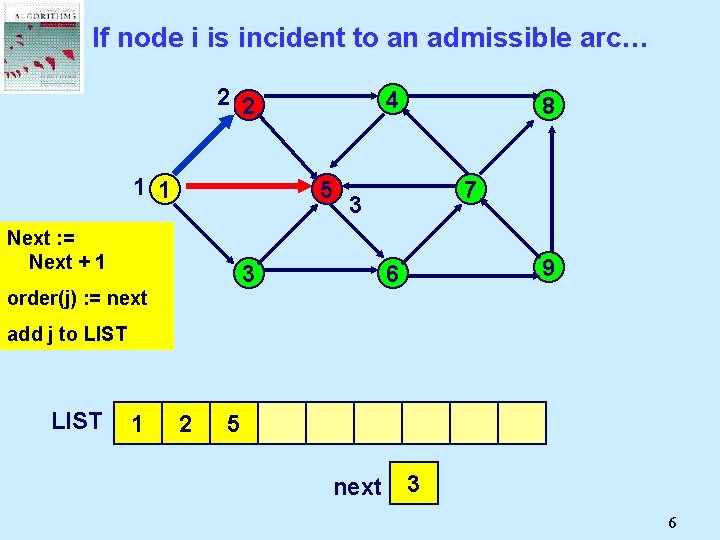
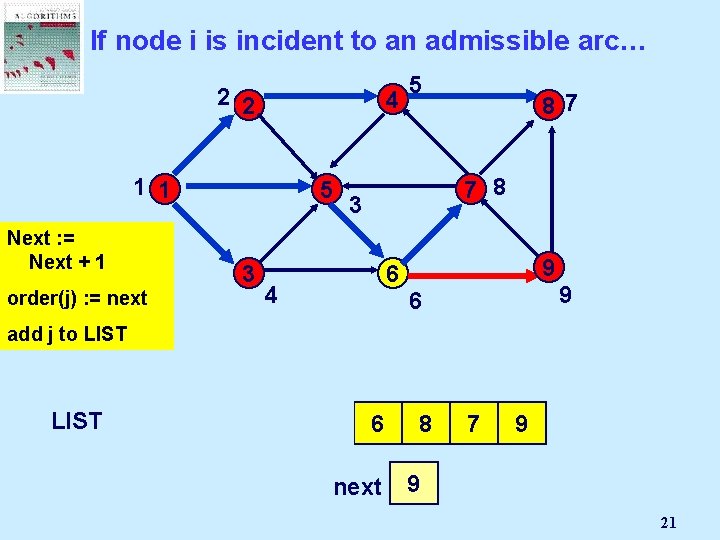
If node i is incident to an admissible arc… 2 2 1 1 4 5 Next : =Node Select Mark an j Next + 1 admissible 7 3 3 pred(j) : = i order(j) arc (i, j): = next 8 9 6 add j to LIST 1 2 5 next 3 2 6

If node i is incident to an admissible arc… 2 2 4 1 1 5 Next : =Node Select Mark an j Next + 1 admissible 3 pred(j) : = i order(j) arc (i, j): = next 8 7 3 9 6 4 add j to LIST 1 2 5 3 next 3 2 4 7

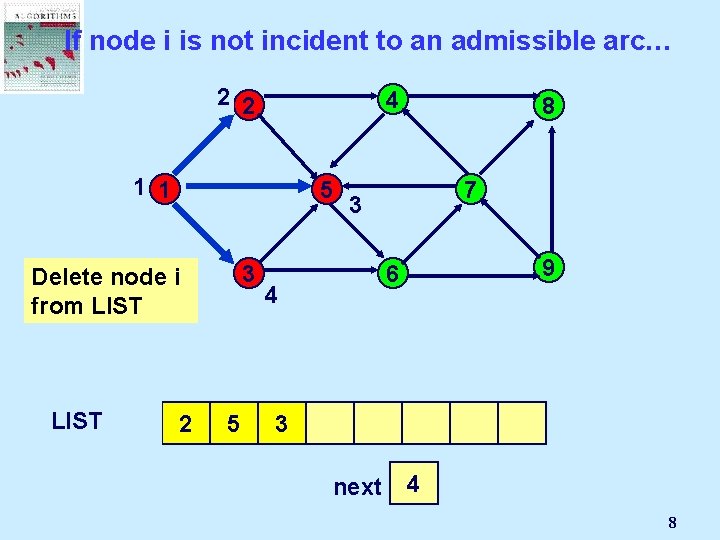
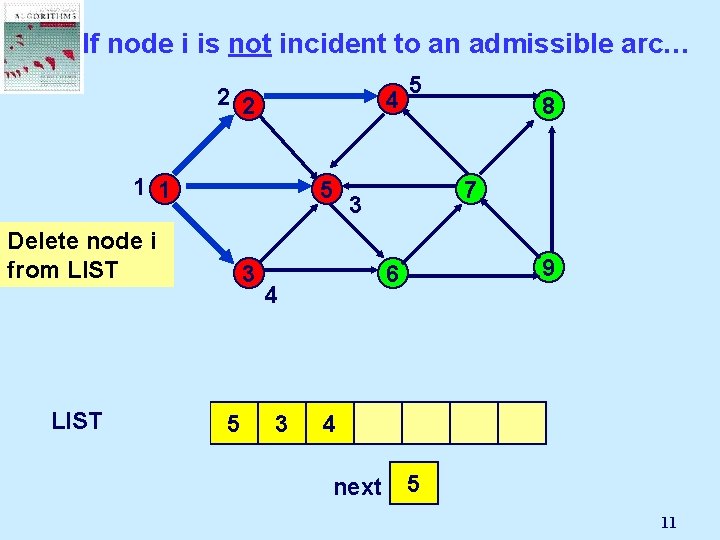
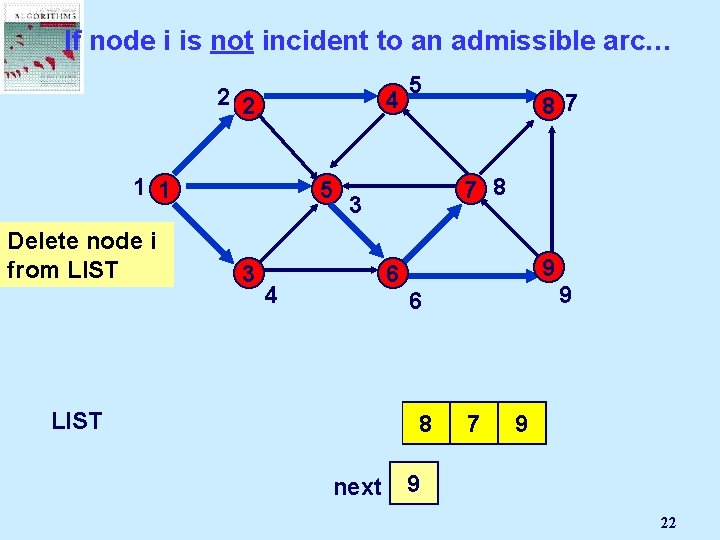
If node i is not incident to an admissible arc… 2 2 4 1 1 5 3 Delete node i from LIST 1 2 5 8 7 3 9 6 4 3 next 3 2 4 8

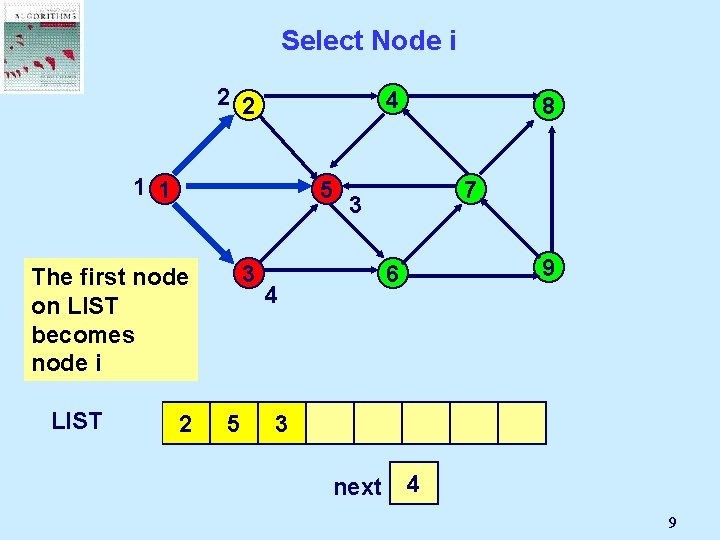
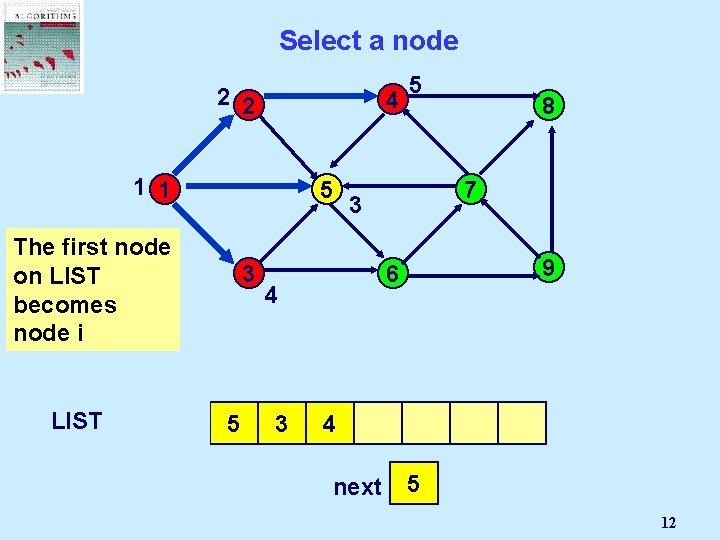
Select Node i 2 2 4 1 1 5 3 The first node on LIST becomes node i LIST 1 2 5 8 7 3 9 6 4 3 next 3 2 4 9

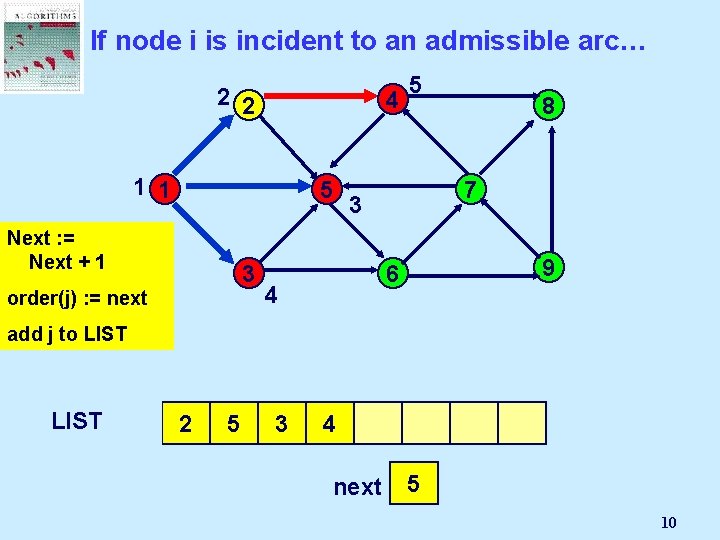
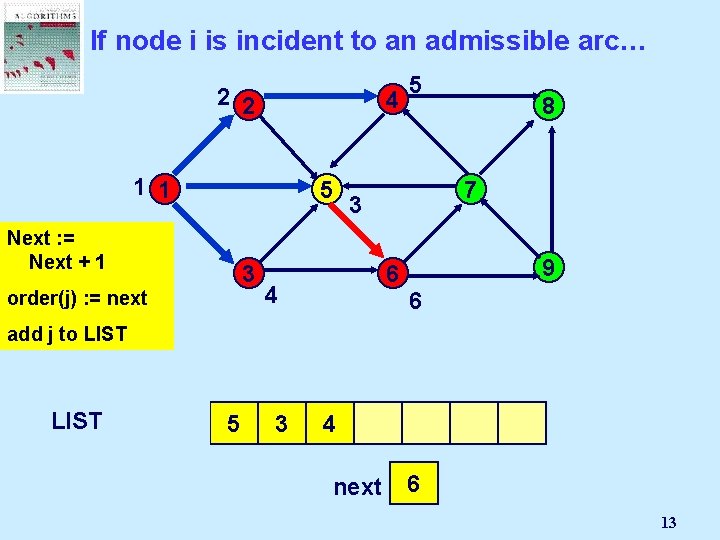
If node i is incident to an admissible arc… 2 2 4 1 1 5 Next : =Node Select Mark an j Next + 1 admissible 3 pred(j) : = i order(j) arc (i, j): = next 5 7 3 9 6 4 8 add j to LIST 1 2 5 3 4 next 3 2 4 5 10

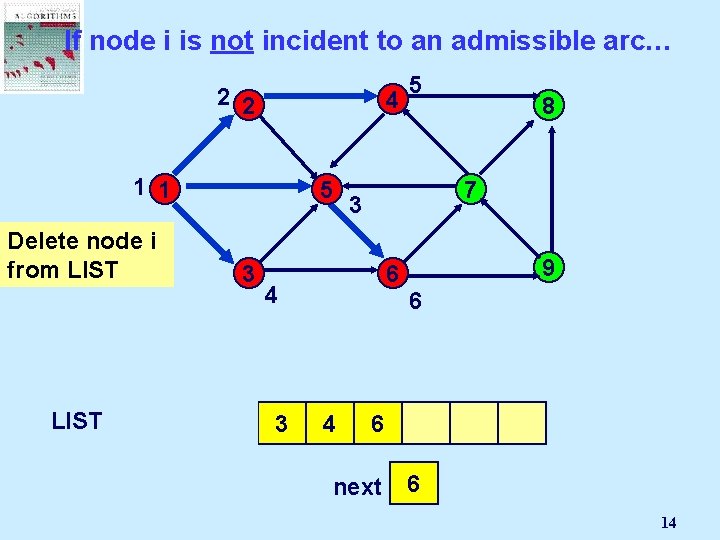
If node i is not incident to an admissible arc… 2 2 4 1 1 5 Delete node i from LIST 1 3 2 5 8 7 3 9 6 4 3 5 4 next 3 2 4 5 11

Select a node 2 2 4 1 1 5 The first node on LIST becomes node i LIST 1 3 2 5 8 7 3 9 6 4 3 5 4 next 3 2 4 5 12

If node i is incident to an admissible arc… 2 2 4 1 1 5 Next : =Node Select Mark an j Next + 1 admissible 3 pred(j) : = i order(j) arc (i, j): = next 5 7 3 9 6 4 8 6 add j to LIST 1 2 5 3 4 next 3 2 4 5 6 13

If node i is not incident to an admissible arc… 2 2 4 1 1 5 Delete node i from LIST 1 3 2 5 8 7 3 9 6 4 3 5 6 4 6 next 3 2 4 5 6 14

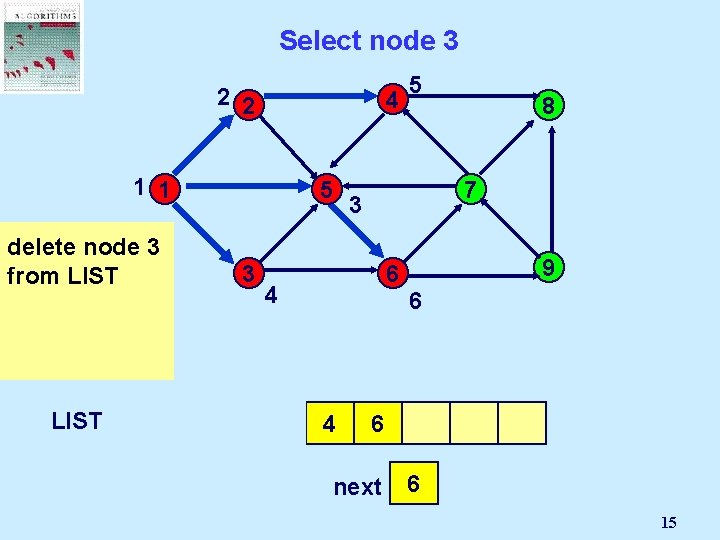
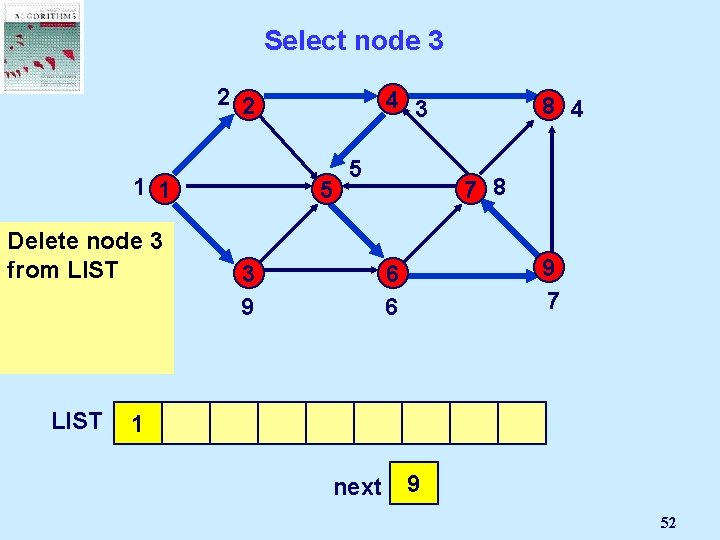
Select node 3 2 2 4 1 1 5 node is not 3 delete 3 node incident to from LIST any admissible arcs LIST 1 3 2 5 8 7 3 9 6 4 3 5 6 4 6 next 3 2 4 5 6 15

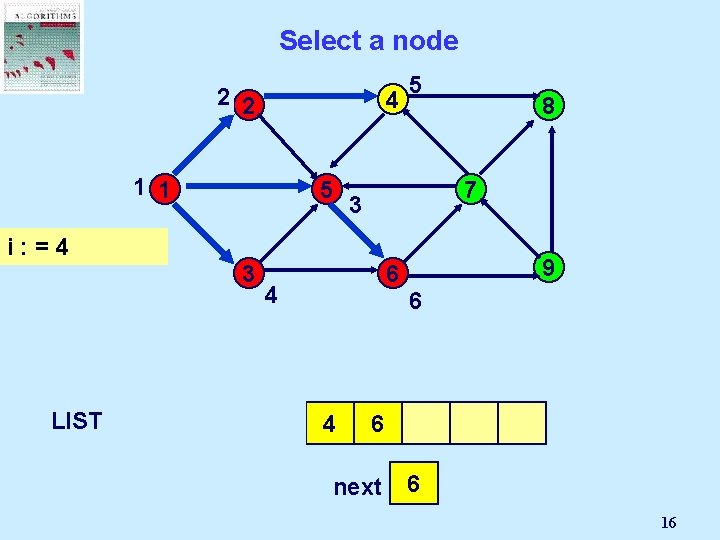
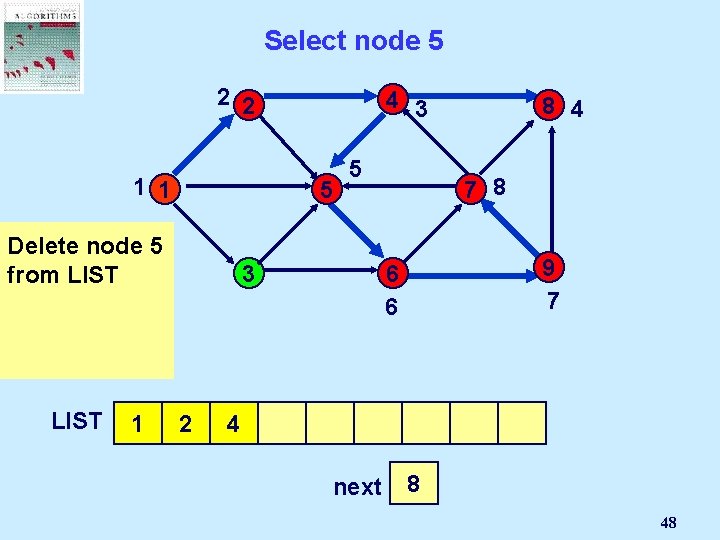
Select a node 2 2 4 1 1 5 5 7 3 i: =4 3 LIST 1 2 5 9 6 4 3 8 6 4 6 next 3 2 4 5 6 16

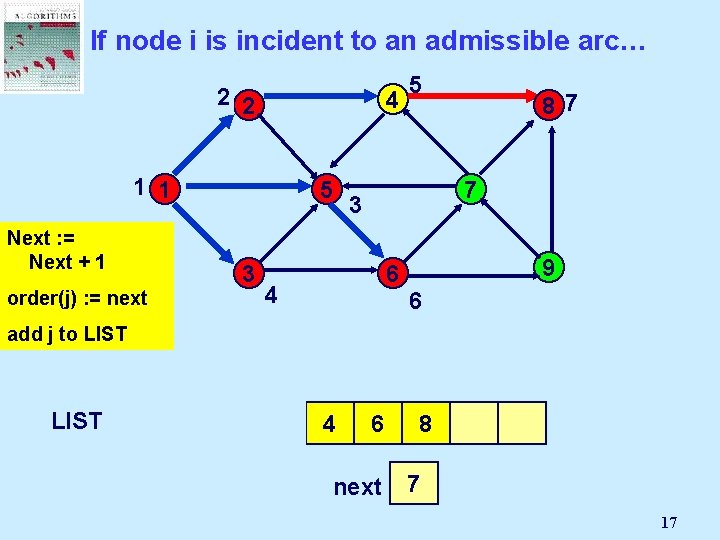
If node i is incident to an admissible arc… 2 2 4 1 1 5 Next : =Node Select Mark an j Next + 1 admissible 3 pred(j) : = i order(j) arc (i, j): = next 5 87 7 3 9 6 4 6 add j to LIST 1 2 5 3 4 6 next 8 3 2 4 5 6 7 17

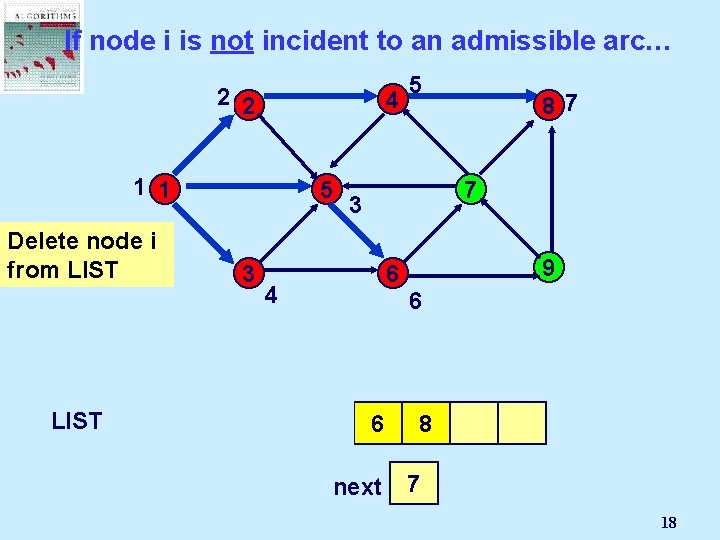
If node i is not incident to an admissible arc… 2 2 4 1 1 5 Delete node i from LIST 1 3 2 5 87 7 3 9 6 4 3 5 6 4 6 next 8 3 2 4 5 6 7 18

Select node i 2 2 4 1 1 5 5 87 7 3 i : = 6 3 LIST 1 2 5 4 3 9 6 6 4 6 next 8 3 2 4 5 6 7 19

If node i is incident to an admissible arc… 2 2 4 1 1 5 Next : =Node Select Mark an j Next + 1 admissible 3 pred(j) : = i order(j) arc (i, j): = next 5 87 7 8 3 9 6 4 6 add j to LIST 1 2 5 3 4 6 next 8 7 3 2 4 5 6 7 8 20

If node i is incident to an admissible arc… 2 2 4 1 1 5 Next : =Node Select Mark an j Next + 1 admissible 3 pred(j) : = i order(j) arc (i, j): = next 5 87 7 8 3 9 6 4 9 6 add j to LIST 1 2 5 3 4 6 next 8 7 9 3 2 4 5 6 7 8 9 21

If node i is not incident to an admissible arc… 2 2 4 1 1 5 Delete node i from LIST 1 3 2 5 87 7 8 3 9 6 4 3 5 9 6 4 6 next 8 7 9 3 2 4 5 6 7 8 9 22

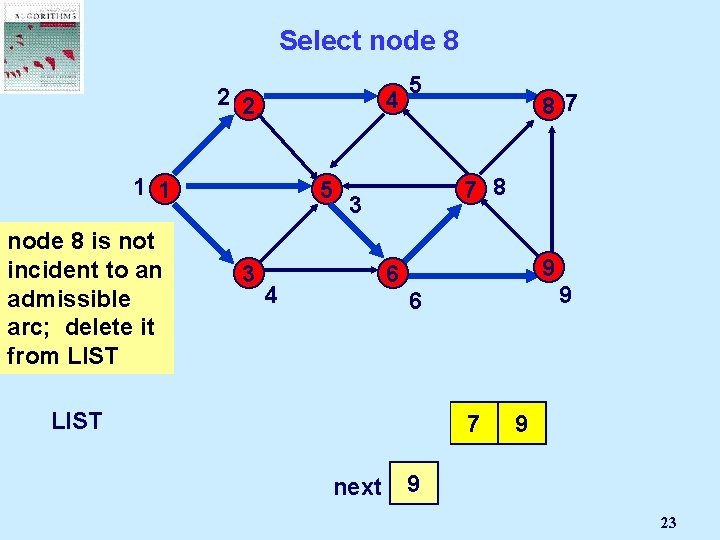
Select node 8 2 2 4 1 1 5 node 8 is not incident to an admissible arc; delete it from LIST 1 3 2 5 87 7 8 3 9 6 4 3 5 9 6 4 6 next 8 7 9 3 2 4 5 6 7 8 9 23

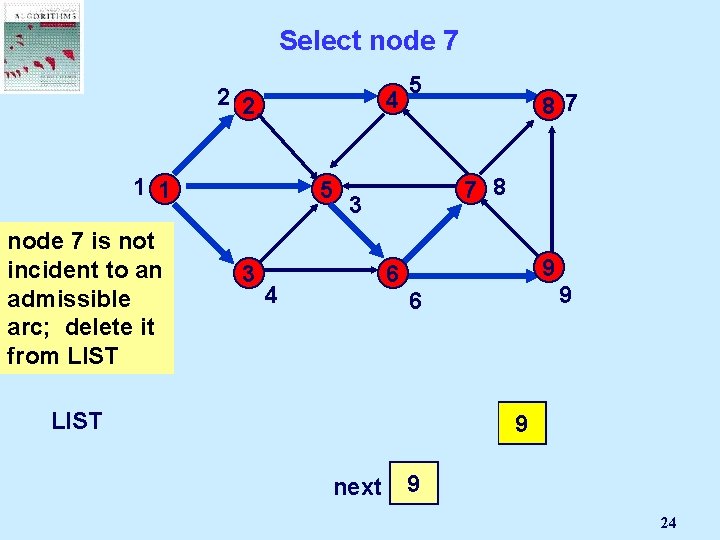
Select node 7 2 2 4 1 1 5 node 7 is not incident to an admissible arc; delete it from LIST 1 3 2 5 87 7 8 3 9 6 4 3 5 9 6 4 6 next 8 7 9 3 2 4 5 6 7 8 9 24

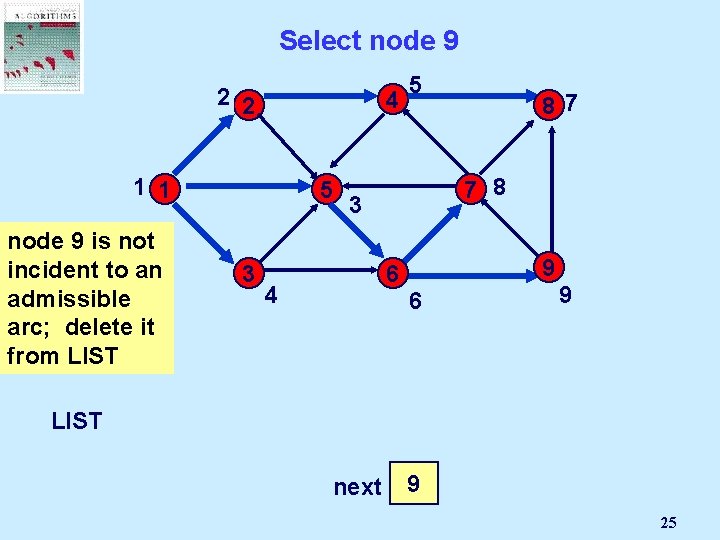
Select node 9 2 2 4 1 1 5 node 9 is not incident to an admissible arc; delete it from LIST 1 3 2 5 87 7 8 3 9 6 4 3 5 9 6 4 6 next 8 7 9 3 2 4 5 6 7 8 9 25

Depth First Search Breadth first search animation

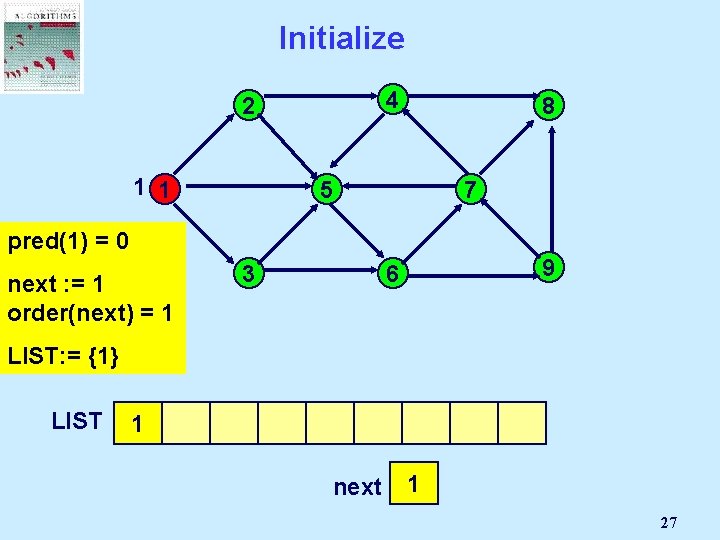
Initialize 4 2 1 1 pred(1) =all Unmark 0 nodes in N; next : = 1 Mark node s= 1 order(next) 8 5 3 7 9 6 LIST: = {1} LIST 1 next 1 27

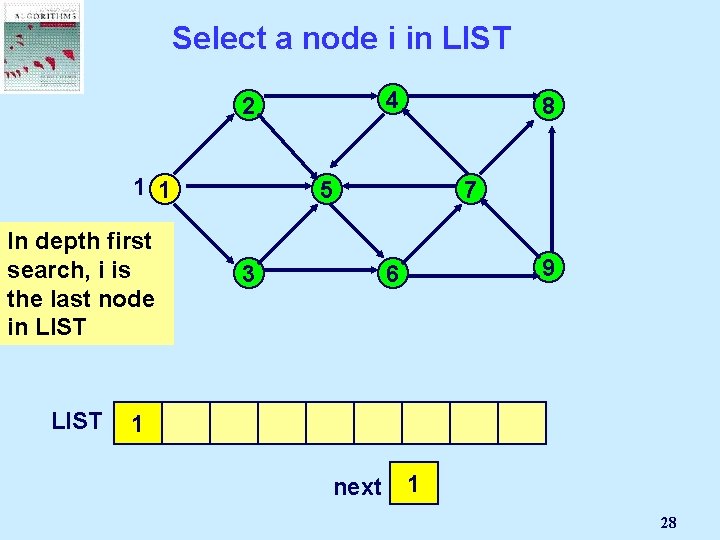
Select a node i in LIST 4 2 1 1 In depth first search, i is the last node in LIST 8 5 3 7 9 6 1 next 1 28

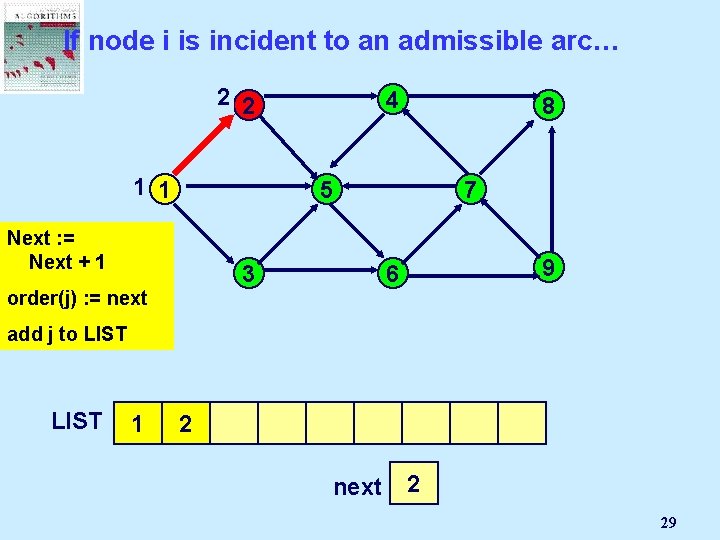
If node i is incident to an admissible arc… 2 2 1 1 4 8 5 Next : =Node Select Mark an j Next + 1 admissible 3 pred(j) : = i order(j) arc (i, j): = next 7 9 6 add j to LIST 1 2 next 2 1 29

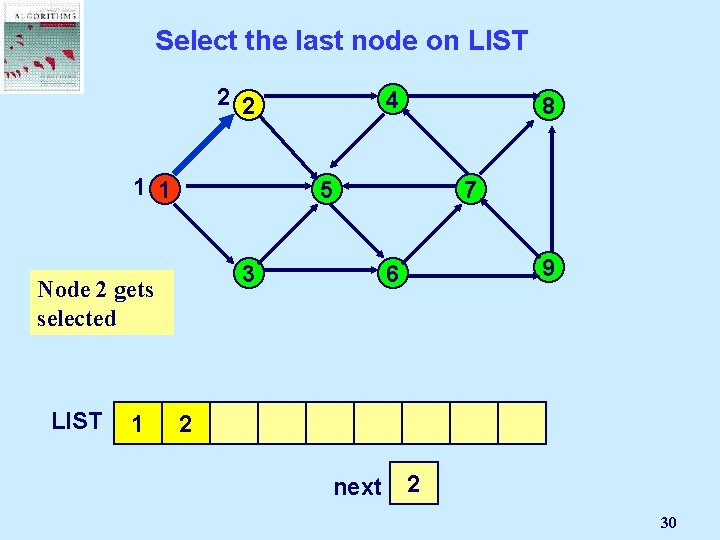
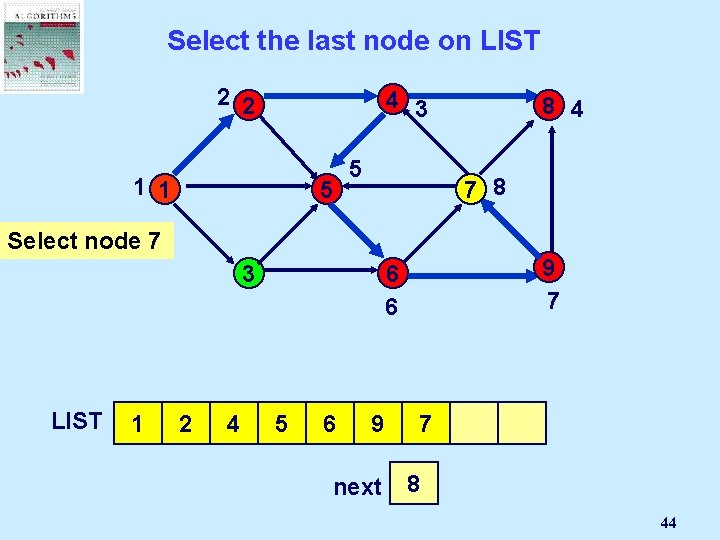
Select the last node on LIST 2 2 1 1 1 8 5 3 Node 2 gets selected LIST 4 7 9 6 2 next 2 1 30

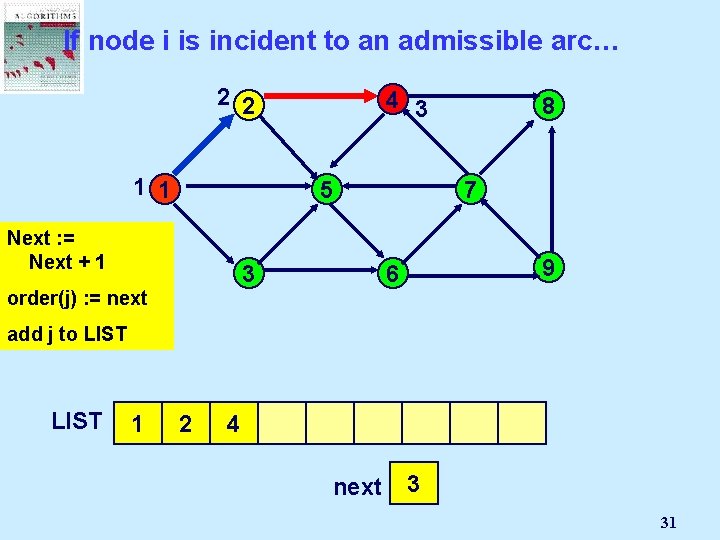
If node i is incident to an admissible arc… 2 2 1 1 4 3 5 Next : =Node Select Mark an j Next + 1 admissible 3 pred(j) : = i order(j) arc (i, j): = next 8 7 9 6 add j to LIST 1 2 4 next 2 1 3 31

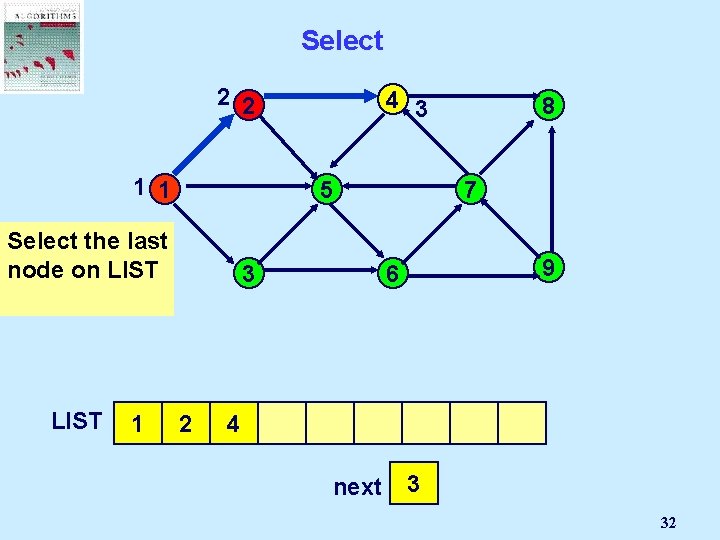
Select 2 2 1 1 5 Select the last node on LIST 1 4 3 3 2 8 7 9 6 4 next 2 1 3 32

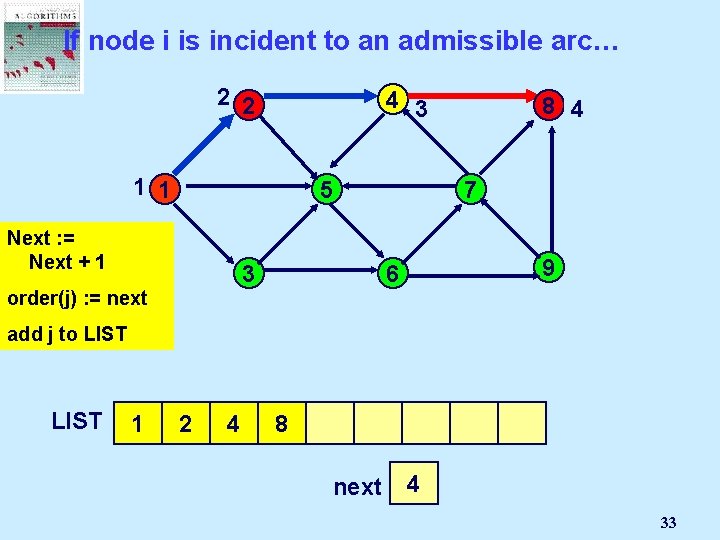
If node i is incident to an admissible arc… 2 2 4 3 1 1 5 Next : =Node Select Mark an j Next + 1 admissible 3 pred(j) : = i order(j) arc (i, j): = next 8 4 7 9 6 add j to LIST 1 2 4 8 next 2 1 3 4 33

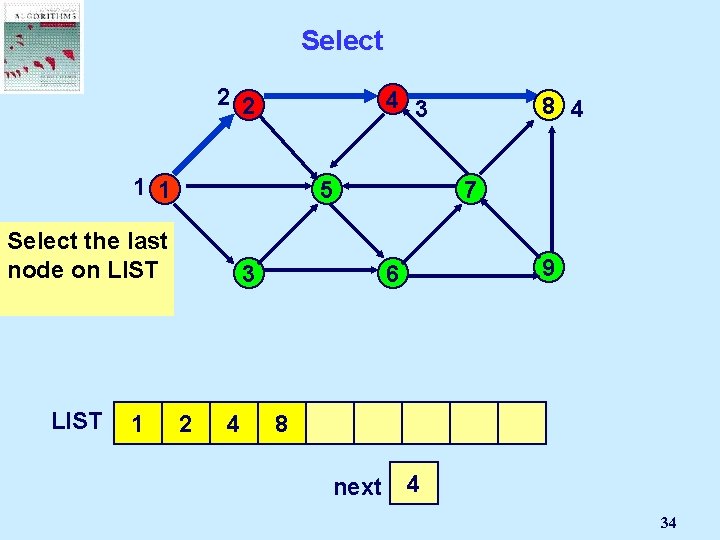
Select 2 2 4 3 1 1 5 Select the last node on LIST 1 3 2 4 8 4 7 9 6 8 next 2 1 3 4 34

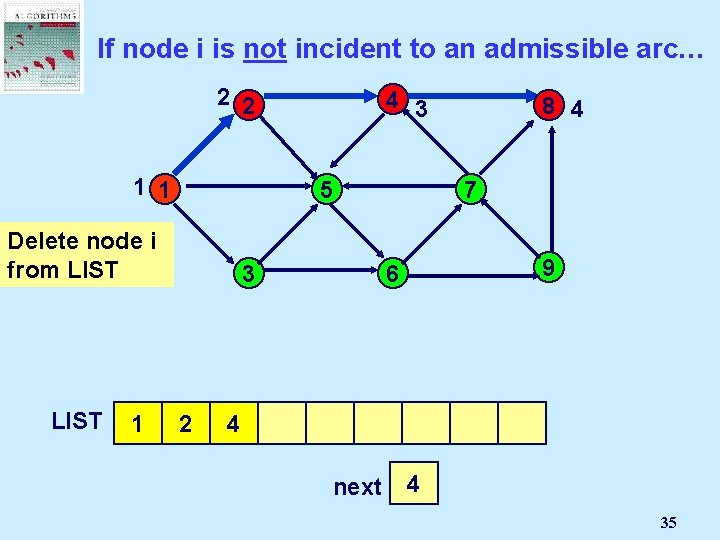
If node i is not incident to an admissible arc… 2 2 4 3 1 1 5 Delete node i from LIST 1 3 2 4 8 4 7 9 6 8 next 2 1 3 4 35

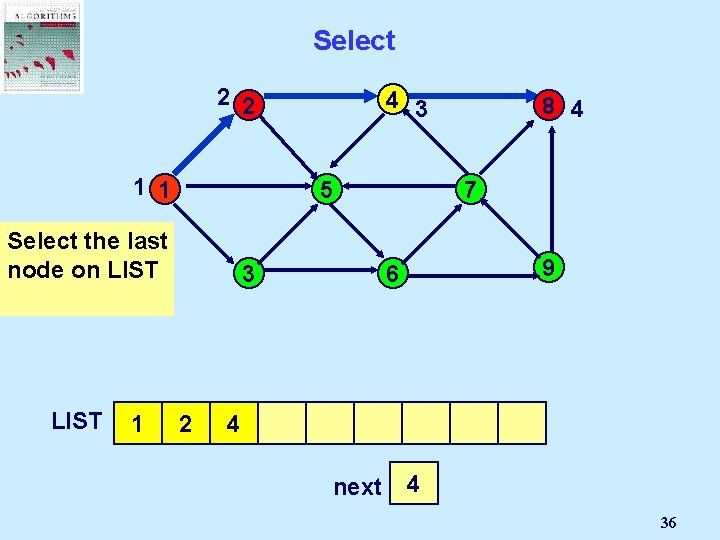
Select 2 2 4 3 1 1 5 Select the last node on LIST 1 3 2 4 8 4 7 9 6 8 next 2 1 3 4 36

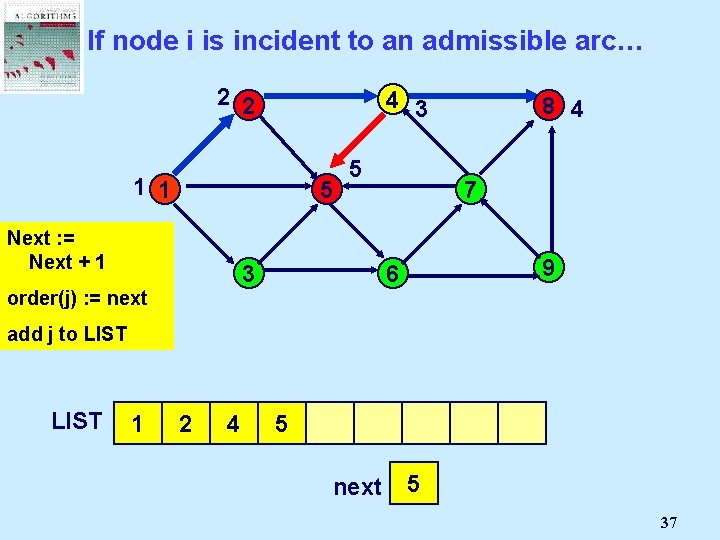
If node i is incident to an admissible arc… 2 2 4 3 1 1 5 Next : =Node Select Mark an j Next + 1 admissible 5 3 pred(j) : = i order(j) arc (i, j): = next 8 4 7 9 6 add j to LIST 1 2 4 8 5 next 2 1 3 4 5 37

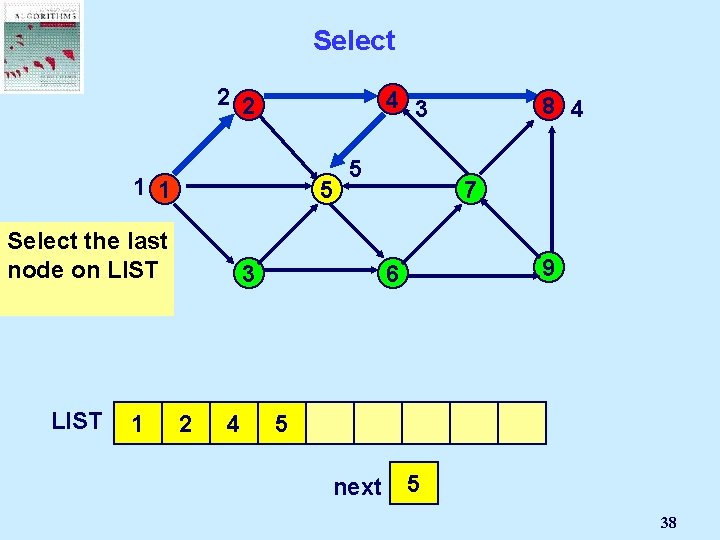
Select 2 2 4 3 1 1 5 Select the last node on LIST 1 5 3 2 4 8 4 7 9 6 8 5 next 2 1 3 4 5 38

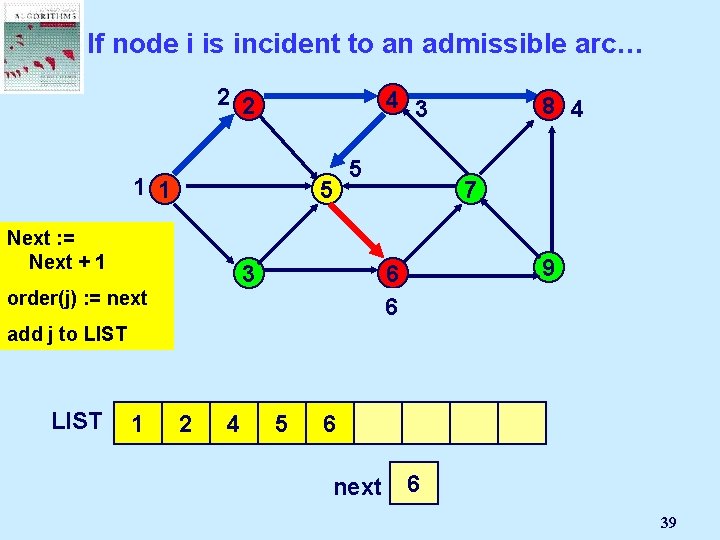
If node i is incident to an admissible arc… 2 2 4 3 1 1 5 Next : =Node Select Mark an j Next + 1 admissible 5 3 pred(j) : = i order(j) arc (i, j): = next 8 4 7 9 6 6 add j to LIST 1 2 4 8 5 6 next 2 1 3 4 5 6 39

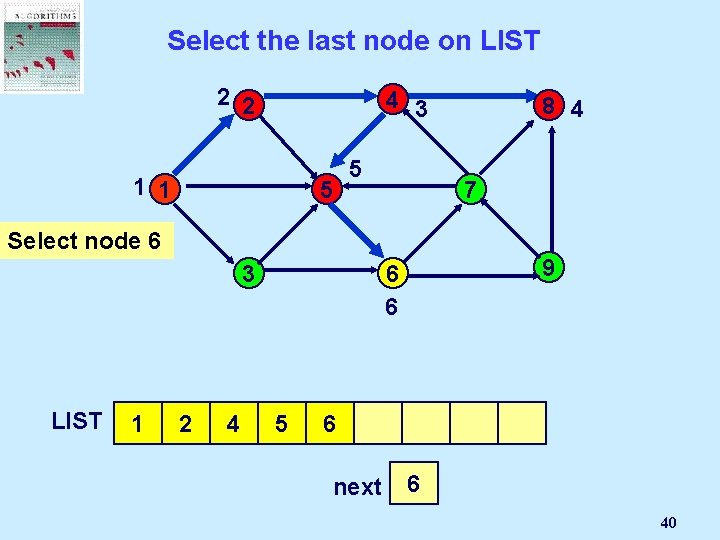
Select the last node on LIST 2 2 4 3 1 1 5 5 8 4 7 Select node 6 3 LIST 1 2 4 9 6 6 8 5 6 next 2 1 3 4 5 6 40

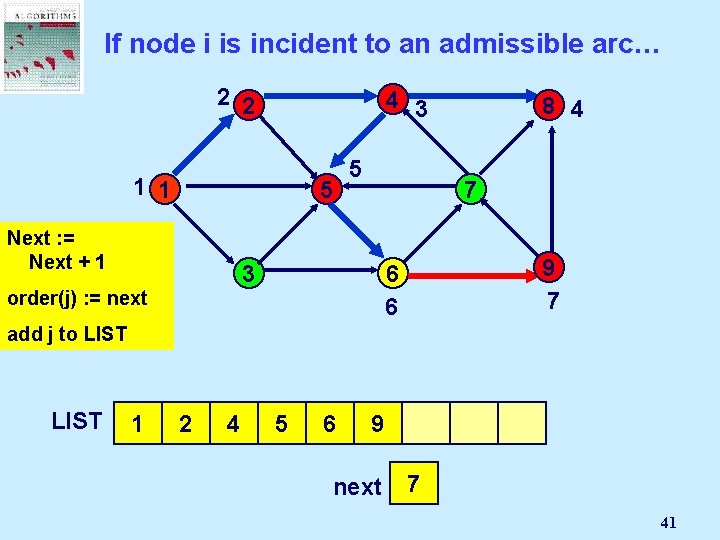
If node i is incident to an admissible arc… 2 2 4 3 1 1 5 Next : =Node Select Mark an j Next + 1 admissible 5 7 3 pred(j) : = i order(j) arc (i, j): = next 8 4 9 7 6 6 add j to LIST 1 2 4 8 5 6 9 next 2 1 3 4 5 6 7 41

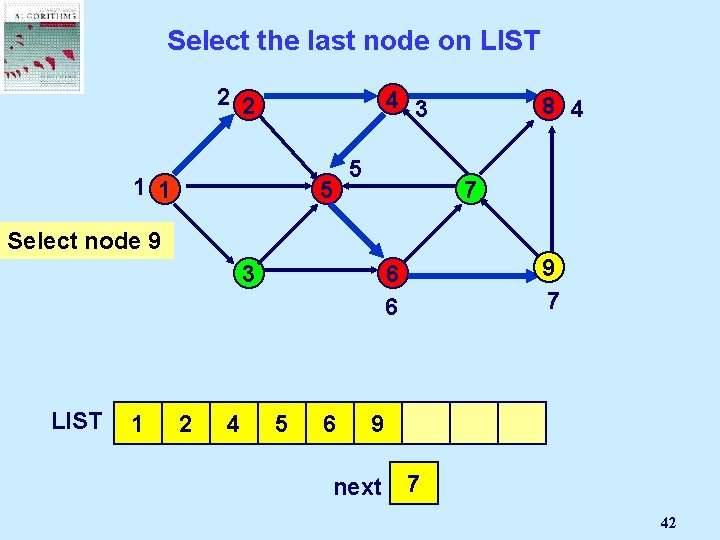
Select the last node on LIST 2 2 4 3 1 1 5 5 8 4 7 Select node 9 3 LIST 1 2 4 9 7 6 6 8 5 6 9 next 2 1 3 4 5 6 7 42

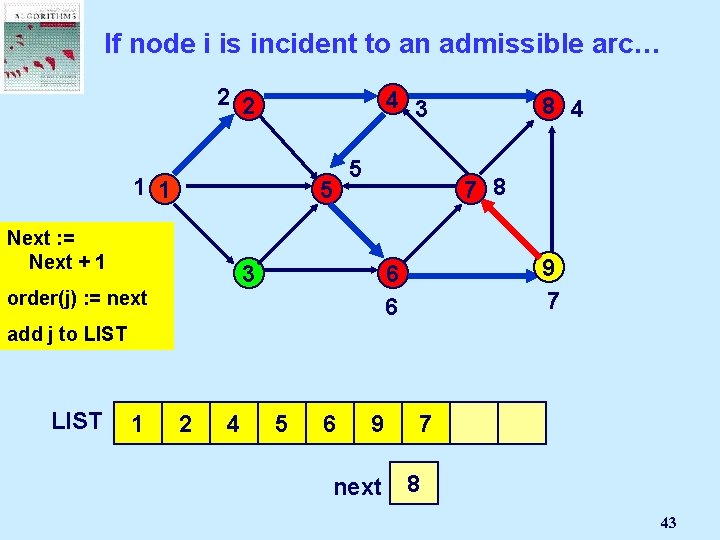
If node i is incident to an admissible arc… 2 2 4 3 1 1 5 Next : =Node Select Mark an j Next + 1 admissible 5 7 8 3 pred(j) : = i order(j) arc (i, j): = next 8 4 9 7 6 6 add j to LIST 1 2 4 8 5 6 9 next 7 2 1 3 4 5 6 7 8 43

Select the last node on LIST 2 2 4 3 1 1 5 5 8 4 7 8 Select node 7 3 LIST 1 2 4 9 7 6 6 8 5 6 9 next 7 2 1 3 4 5 6 7 8 44

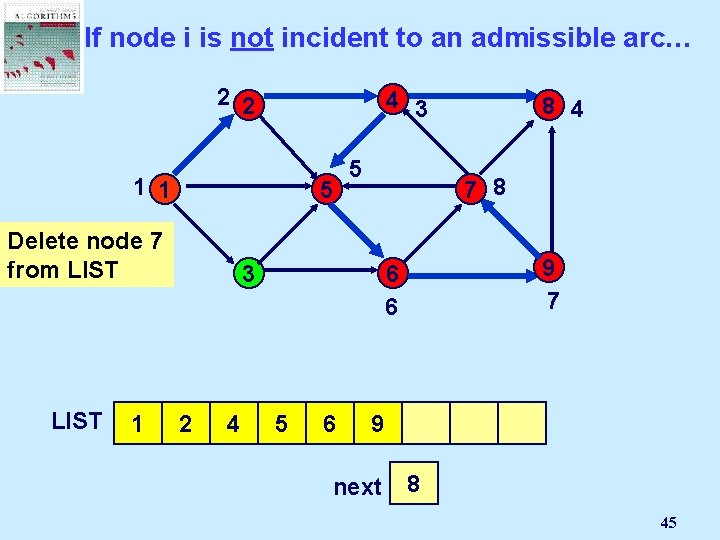
If node i is not incident to an admissible arc… 2 2 4 3 1 1 5 Delete node 7 from LIST 1 5 7 8 3 2 4 9 7 6 6 8 5 6 8 4 9 next 7 2 1 3 4 5 6 7 8 45

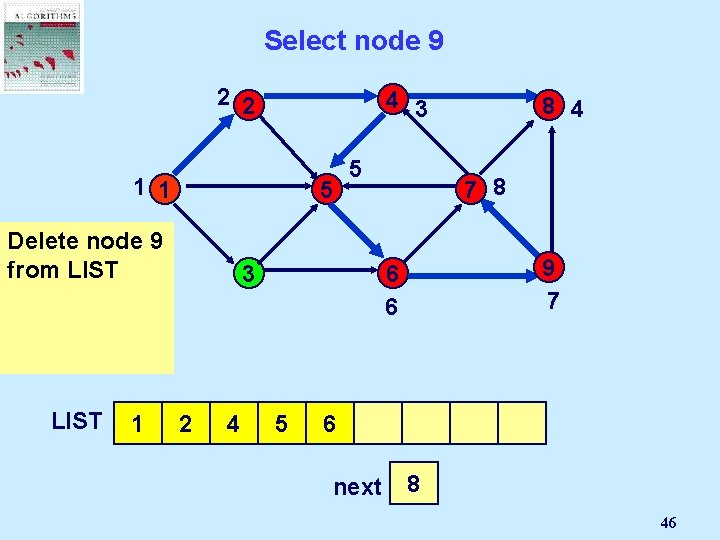
Select node 9 2 2 4 3 1 1 5 Delete But node 9 is 9 not incident from LIST to an admissible arc. LIST 1 5 7 8 3 2 4 9 7 6 6 8 5 6 8 4 9 next 7 2 1 3 4 5 6 7 8 46

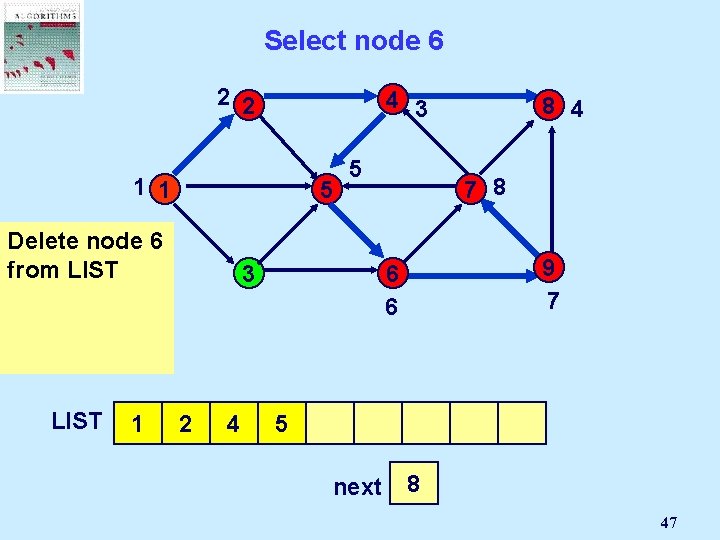
Select node 6 2 2 4 3 1 1 5 Delete But node 6 is 6 not incident from LIST to an admissible arc. LIST 1 5 7 8 3 2 4 9 7 6 6 8 5 6 8 4 9 next 7 2 1 3 4 5 6 7 8 47

Select node 5 2 2 4 3 1 1 5 But node 5 is 5 Delete node not fromincident LIST to an admissible arc. LIST 1 5 7 8 3 2 4 9 7 6 6 8 5 6 8 4 9 next 7 2 1 3 4 5 6 7 8 48

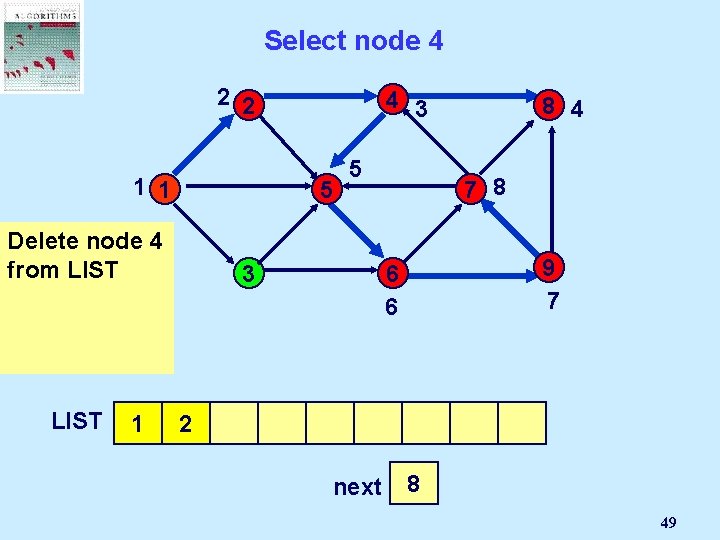
Select node 4 2 2 4 3 1 1 5 Delete But node 4 is 4 not incident from LIST to an admissible arc. LIST 1 5 7 8 3 2 4 9 7 6 6 8 5 6 8 4 9 next 7 2 1 3 4 5 6 7 8 49

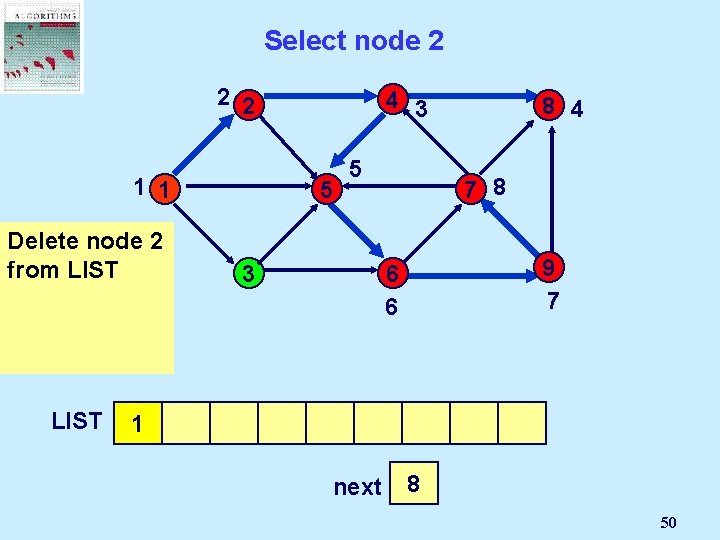
Select node 2 2 2 4 3 1 1 5 Delete But node 2 is 2 not incident from LIST to an admissible arc. LIST 1 5 7 8 3 2 4 9 7 6 6 8 5 6 8 4 9 next 7 2 1 3 4 5 6 7 8 50

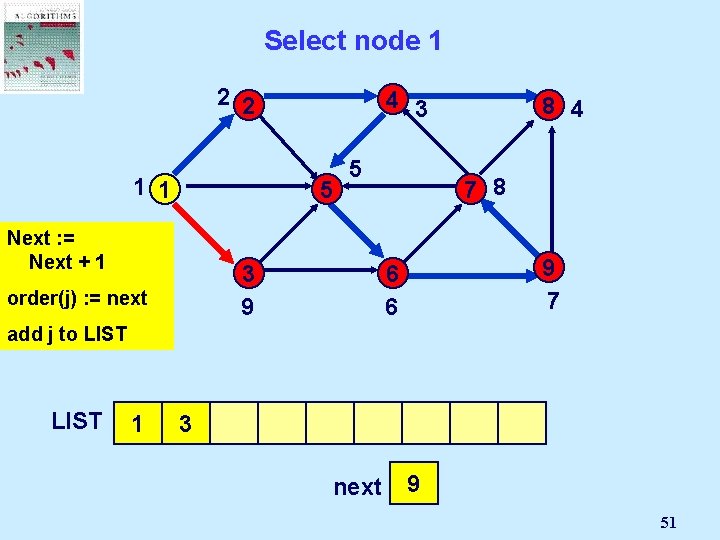
Select node 1 2 2 4 3 1 1 5 Next : =Node Select Mark an j Next + 1 admissible 5 7 8 3 9 pred(j) : = i order(j) arc (i, j): = next 8 4 9 7 6 6 add j to LIST 1 2 3 4 8 5 6 9 next 7 2 1 3 4 5 6 7 8 9 51

Select node 3 2 2 4 3 1 1 5 Delete But node 3 is 3 not incident from LIST to an admissible arc. LIST 1 5 7 8 3 9 2 3 4 9 7 6 6 8 5 6 8 4 9 next 7 2 1 3 4 5 6 7 8 9 52

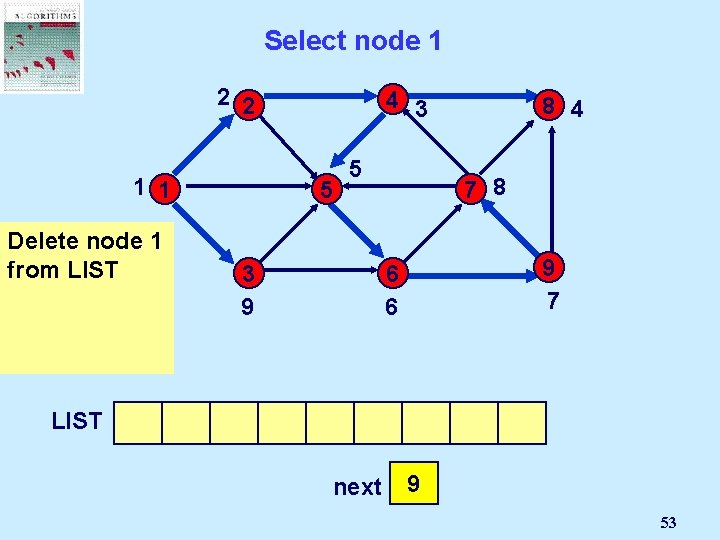
Select node 1 2 2 4 3 1 1 5 Delete But node 1 is 1 not incident from LIST to an admissible arc. LIST 1 5 7 8 3 9 2 3 4 9 7 6 6 8 5 6 8 4 9 next 7 2 1 3 4 5 6 7 8 9 53

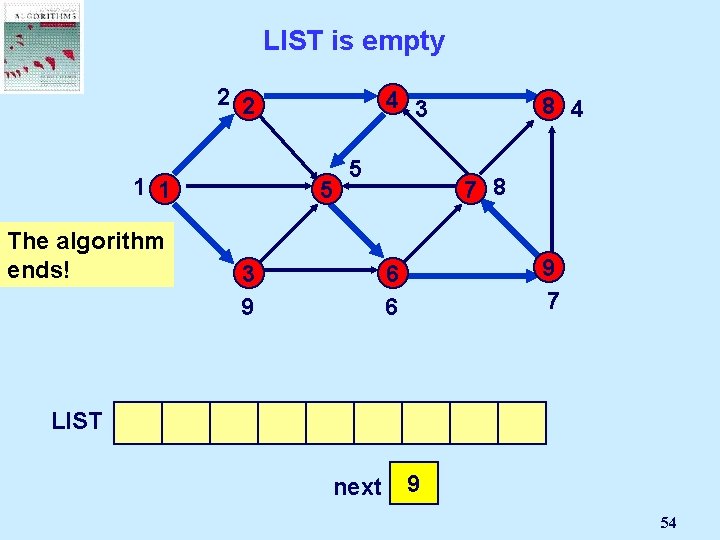
LIST is empty 2 2 4 3 1 1 5 The algorithm ends! LIST 1 5 7 8 3 9 2 3 4 9 7 6 6 8 5 6 8 4 9 next 7 2 1 3 4 5 6 7 8 9 54

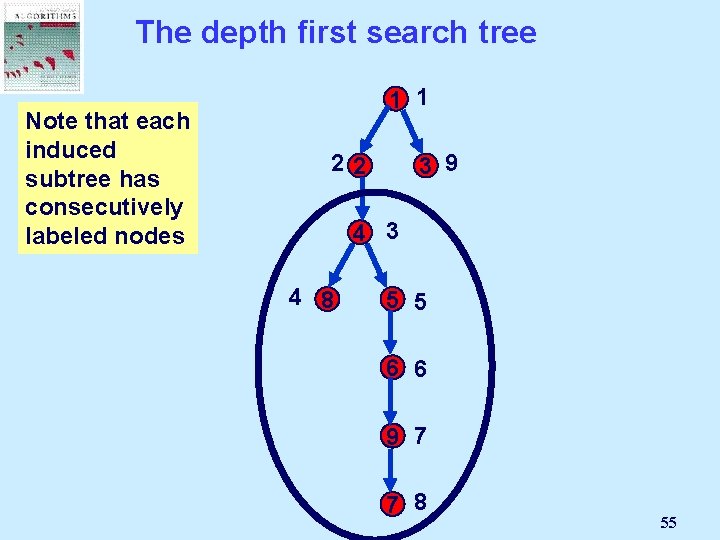
The depth first search tree Note that each induced subtree has consecutively labeled nodes 1 1 22 3 9 4 3 4 8 5 5 6 6 9 7 7 8 55

Topological Ordering Breadth first search animation

Preliminary to Topological Sorting LEMMA. If each node has at least one arc going out, then the first inadmissible arc of a depth first search determines a directed cycle. 1 4 6 7 3 COROLLARY 1. If G has no directed cycle, then there is a node in G with no arcs going. And there is at least one node in G with no arcs coming in. COROLLARY 2. If G has no directed cycle, then one can relabel the nodes so that for each arc (i, j), i < j. 57

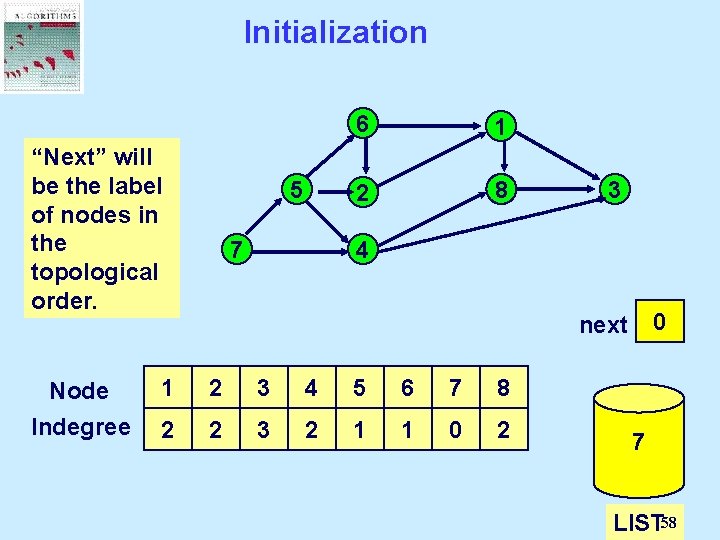
Initialization “Next” Determine LIST is will thethe set be of indegree nodes label with of each in nodes node indegree the of 0. topological order. Node Indegree 5 7 6 1 2 8 3 4 0 next 1 2 3 4 5 6 7 8 2 2 3 2 1 1 0 2 7 LIST 58

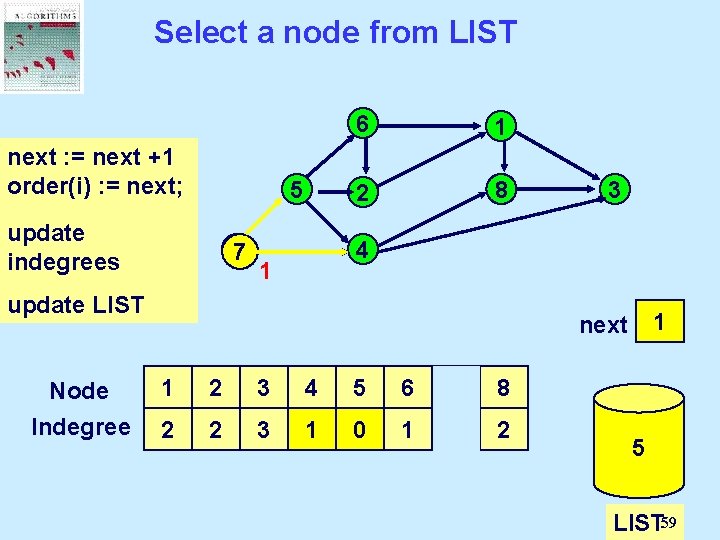
Select a node from LIST next Select : = next a +1 order(i) node from : = next; LIST and update delete it. indegrees 5 77 6 1 2 8 4 1 update LIST Node Indegree 3 0 1 next 1 2 3 4 5 6 7 8 2 2 3 2 1 1 0 2 7 5 LIST 59

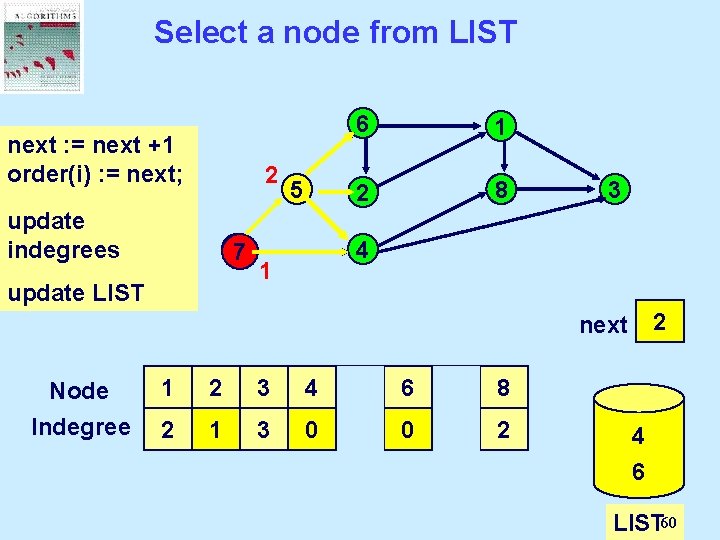
Select a node from LIST next : = next Select a +1 order(i) : = next; node from 2 LIST and update delete it. indegrees 77 update LIST 5 6 1 2 8 3 4 1 0 1 2 next Node Indegree 1 2 3 4 5 6 7 8 2 2 1 3 0 1 2 1 0 0 2 4 7 5 6 LIST 60

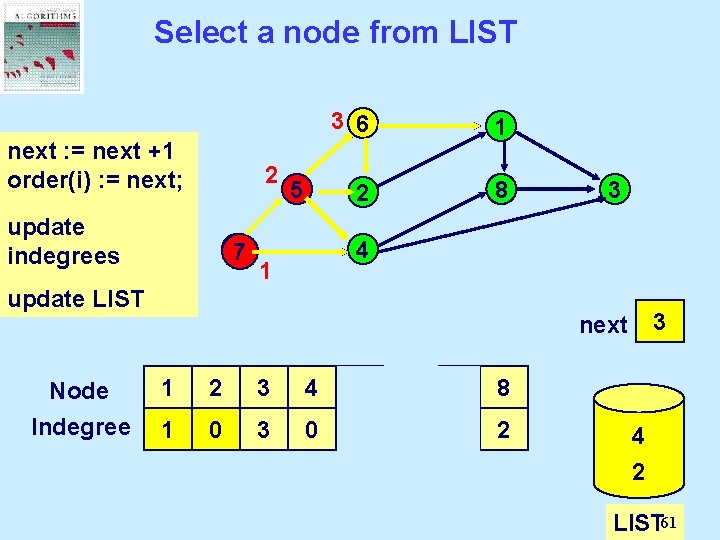
Select a node from LIST next : = next Select a +1 order(i) : = next; node from LIST and update delete it. indegrees 2 77 5 3 6 1 2 8 4 1 update LIST Node Indegree 3 0 1 2 3 next 1 2 3 4 5 6 7 8 2 1 0 3 0 1 2 1 0 0 2 4 7 5 6 2 LIST 61

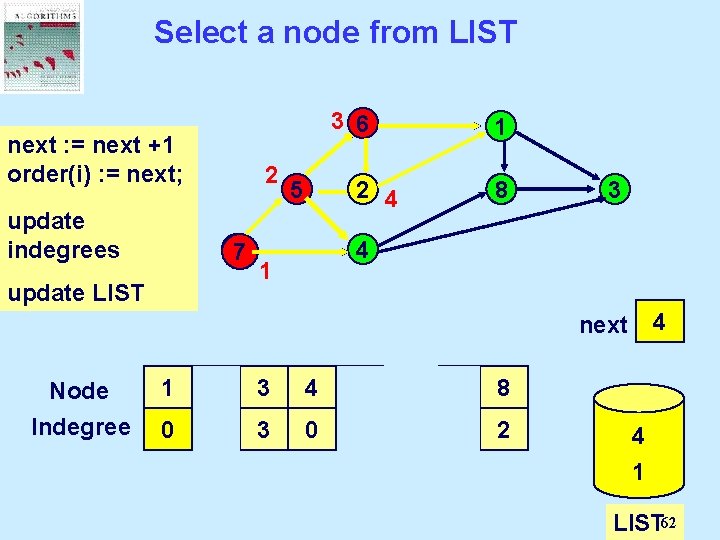
Select a node from LIST 3 6 next : = next Select a +1 order(i) : = next; node from 2 LIST and update delete it. indegrees 77 update LIST 5 1 2 4 8 3 4 1 0 1 2 3 4 next Node Indegree 1 2 3 4 5 6 7 8 2 1 0 3 0 1 2 1 0 0 2 4 7 5 6 2 1 LIST 62

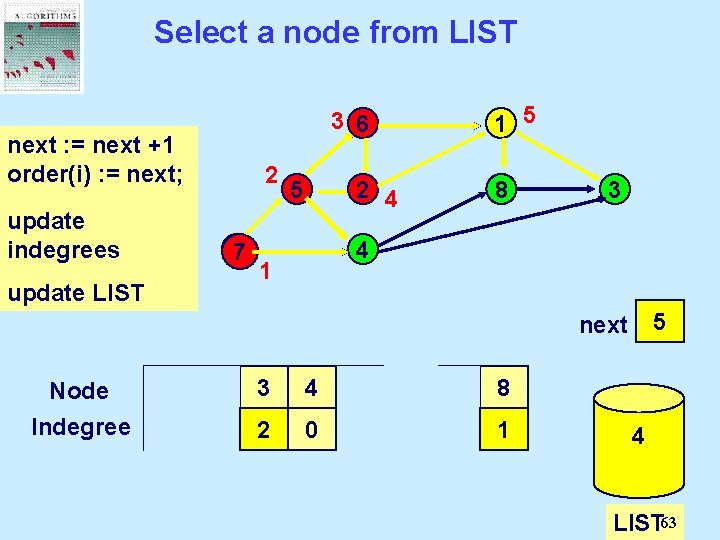
Select a node from LIST 1 5 3 6 next : = next Select a +1 order(i) : = next; node from 2 LIST and update delete it. indegrees 77 update LIST 5 2 4 8 3 4 1 0 1 2 3 4 5 next Node Indegree 1 2 3 4 5 6 7 8 2 1 0 3 2 0 1 2 1 0 0 2 1 4 7 5 6 2 1 LIST 63

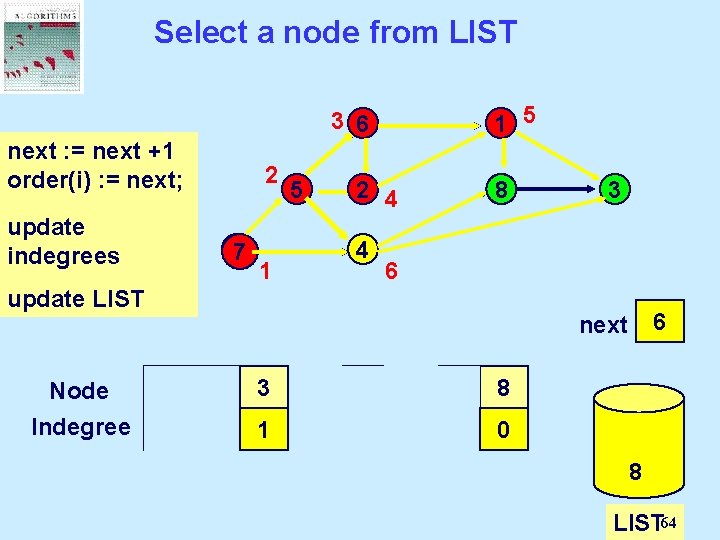
Select a node from LIST 1 5 3 6 next : = next Select a +1 order(i) : = next; node from LIST and update delete it. indegrees 2 77 5 2 4 4 1 8 6 update LIST Node Indegree 3 0 1 2 3 4 5 6 next 1 2 3 4 5 6 7 8 2 1 0 3 2 1 0 1 0 0 2 1 0 1 6 4 2 7 5 8 LIST 64

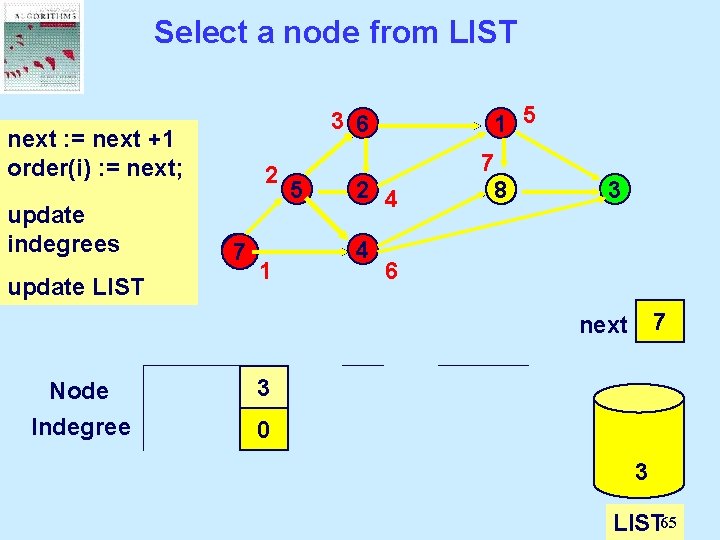
Select a node from LIST 1 5 3 6 next : = next +1 Select: =a next; order(i) node from LIST and update delete it. indegrees 2 77 update LIST 5 7 8 2 4 4 1 3 6 0 1 2 3 4 5 6 7 next Node Indegree 1 2 3 4 5 6 7 8 2 1 0 3 2 1 0 0 1 2 1 0 0 2 1 0 83 LIST 65

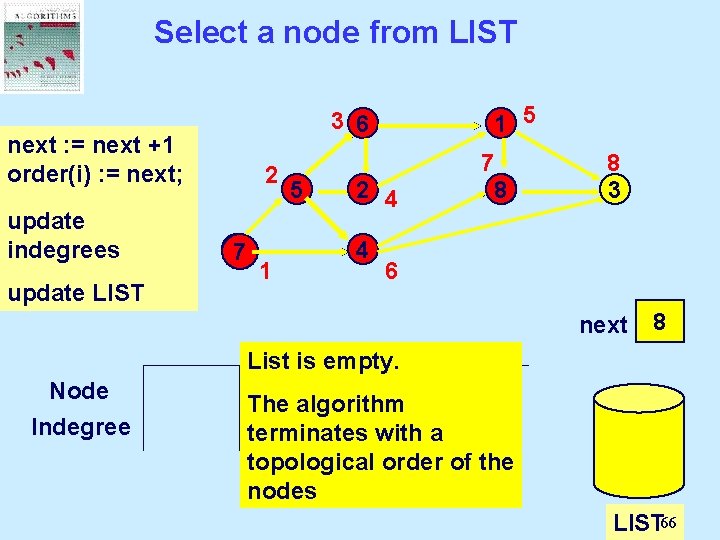
Select a node from LIST 1 5 3 6 next : = next Select a +1 order(i) : = next; node from 2 LIST and update delete it. indegrees 77 update LIST 1 5 2 4 4 7 8 8 3 6 0 1 2 3 4 5 6 7 8 next Node Indegree 1 2 2 1 0 List is empty. 3 4 5 6 7 8 The algorithm 3 2 2 1 0 0 0 1 1 with 1 a 0 0 0 2 1 terminates topological order of the nodes 3 LIST 66