Introduction to Algorithms Greatest common divisor Problem Find

Introduction to Algorithms

Greatest common divisor Problem: Find gcd(m, n) for nonnegative integers m and n, not both zero Eg: gcd(60, 24) = 12, gcd(60, 0) = 60, gcd(0, 0) = ? Euclid’s algorithm gcd(m, n) = gcd(n, m mod n) gcd(m, 0) = m Eg: gcd(60, 24) = gcd(24, 12) = gcd(12, 0) = 12 2

3 descriptions of Euclid’s algorithm gcd(m, n) = gcd(n, m mod n) gcd(m, 0) = m Step 1 If n = 0, return m and stop; otherwise go to Step 2 Divide m by n and assign the remainder to r Step 3 Assign the value of n to m and the value of r to n. Go to Step 1. Find gcd(31415, 14142). while n ≠ 0 do What happens when m < n? r ← m mod n How do we know that this algorithm m← n will eventually stop? n←r return m 3 O(log n) time

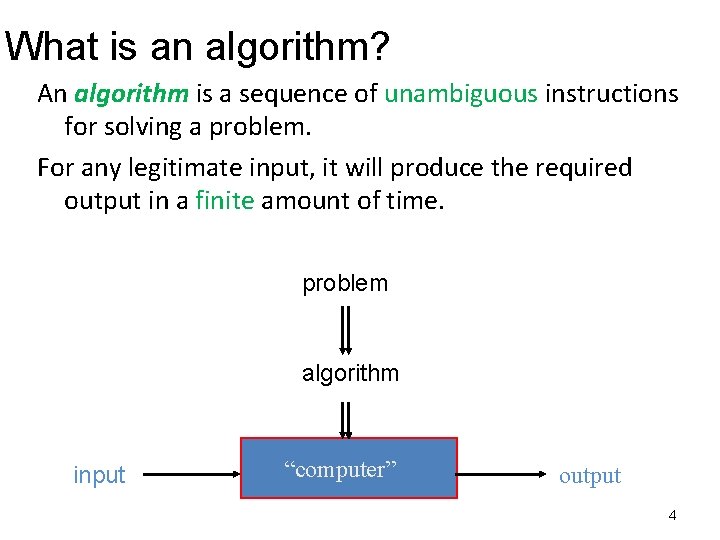
What is an algorithm? An algorithm is a sequence of unambiguous instructions for solving a problem. For any legitimate input, it will produce the required output in a finite amount of time. problem algorithm input “computer” output 4

2 nd method for computing gcd(m, n) Consecutive integer checking algorithm Start with the smaller value min{m, n}. Is this the greatest common divisor? If yes, stop. If no, decrease it by 1 and try again. Step 1 Assign the value of min{m, n} to t Step 2 Divide m by t. If the remainder is 0, go to Step 3; otherwise, go to Step 4 Step 3 Divide n by t. If the remainder is 0, return t and stop; otherwise, go to Step 4 Decrease t by 1 and go to Step 2 Try gcd(60, 24). What happens when m or n = 0? 5

3 rd methods for gcd(m, n) Middle-school procedure Step 1 Find the prime factorization of m Step 2 Find the prime factorization of n Step 3 Find all the common prime factors Step 4 Compute the product of all the common prime factors and return it as gcd(m, n) Formally, is this an algorithm? gcd(60, 24) 60 = 2 · 3 · 5 Ya, but how to find primes? 24 = 2 · 2 · 3 gcd(60, 24) = 2 · 3 = 12. 6

Distance between the two closest elements

Sieve of Eratosthenes Where do we start at each pass? • Let p be number whose multiples are being eliminated on the current pass. • All its smaller multiples 2 p, . . . , (p − 1)p have been eliminated on earlier passes. • We start at p·p=p 2. Where do we finish at each pass? • til n. When do we stop making more passes? • Each pass start at p 2 and stop at n. • Therefore p ≤ n. 8

Sieve of Eratosthenes: Pseudocode Input: Integer n ≥ 2 Output: List of primes less than or equal to n for i ← 2 to n do A[i] ← i // Initialize the array. for p ← 2 to n do // Round down to take the integer part display(A) // Print the array elements if A[p] 0 //p hasn’t been eliminated from the list j ← p *p // Start at p 2 while j ≤ n do // until the end of the list A[j] ← 0 //mark element as eliminated j←j+p // next multiple of p Time complexity: O(n log n) Run this for n=100. 9

Algorithmics: Why study algorithms? • Theoretical importance – the core of computer science • Practical importance – algorithm comes first before programming – a practitioner’s toolkit of known algorithms – framework for designing and analyzing algorithms for new problems – learning how to solve problems in general 10

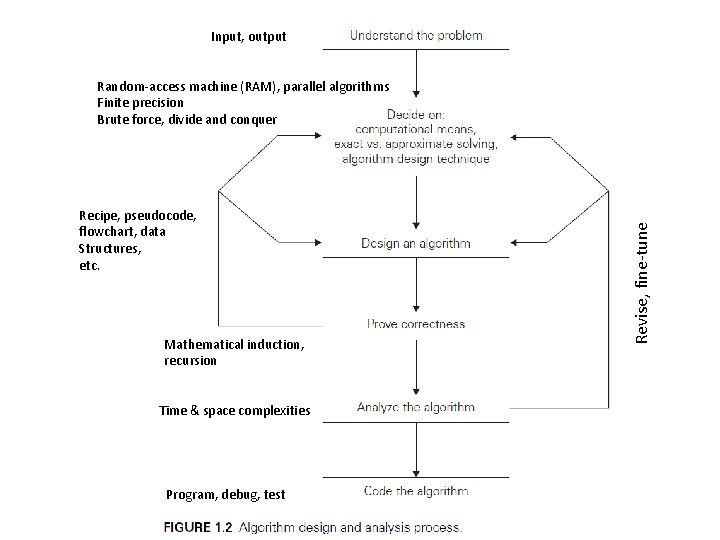
Input, output Recipe, pseudocode, flowchart, data Structures, etc. Mathematical induction, recursion Time & space complexities Program, debug, test Revise, fine-tune Random-access machine (RAM), parallel algorithms Finite precision Brute force, divide and conquer

Summary • An algorithm is a sequence of unambiguous instructions for solving a problem in a finite amount of time. • Algorithms can be specified in a natural language or pseudocode. • They can be implemented as computer programs. • Algorithm design techniques (strategies or paradigms) are general approaches to solving problems. • The same problem can often be solved by several algorithms. • Algorithms operate on data structures. • Algorithms have time and space complexities