Introduction to Algorithms Dynamic Programming Part 2 CSE

Introduction to Algorithms Dynamic Programming – Part 2 CSE 680 Prof. Roger Crawfis

The 0/1 Knapsack Problem l Given: A set S of n items, with each item i having l l wi - a positive weight bi - a positive benefit Goal: Choose items with maximum total benefit but with weight at most W. l If we are not allowed to take fractional amounts, then this is the 0/1 knapsack problem. l l In this case, we let T denote the set of items we take l Objective: maximize l Constraint:

Example l Given: A set S of n items, with each item i having l l l bi - a positive “benefit” wi - a positive “weight” Goal: Choose items with maximum total benefit but with weight at most W. “knapsack” Items: 1 2 3 4 5 Weight: 4 in 2 in 6 in 2 in Benefit: $20 $3 $6 $25 $80 box of width 9 in Solution: • item 5 ($80, 2 in) • item 3 ($6, 2 in) • item 1 ($20, 4 in)

First Attempt Sk: Set of items numbered 1 to k. l Define B[k] = best selection from Sk. l Problem: does not have sub-problem optimality: l l Consider set S={(3, 2), (5, 4), (8, 5), (4, 3), (10, 9)} of (benefit, weight) pairs and total weight W = 20 Best for S 4: Best for S 5:

Second Attempt Sk: Set of items numbered 1 to k. l Define B[k, w] to be the best selection from Sk with weight at most w l This does have sub-problem optimality. l l I. e. , the best subset of Sk with weight at most w is either: l l the best subset of Sk-1 with weight at most w or the best subset of Sk-1 with weight at most w-wk plus item k

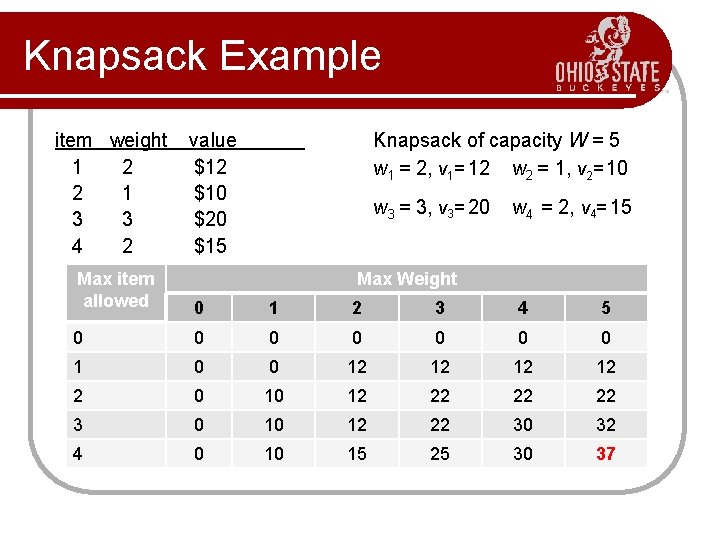
Knapsack Example item weight 1 2 2 1 3 3 4 2 value $12 $10 $20 $15 Knapsack of capacity W = 5 w 1 = 2, v 1= 12 w 2 = 1, v 2= 10 w 3 = 3, v 3= 20 w 4 = 2, v 4= 15 Max item allowed Max Weight 0 1 2 3 4 5 0 0 0 0 12 12 2 0 10 12 22 22 22 3 0 10 12 22 30 32 4 0 10 15 25 30 37

Algorithm Since B[k, w] is defined in terms of B[k-1, *], we can use two arrays of instead of a matrix. l Running time is O(n. W). l Not a polynomialtime algorithm since W may be large. l Called a pseudopolynomial time algorithm. l Algorithm 01 Knapsack(S, W): Input: set S of n items with benefit bi and weight wi; maximum weight W Output: benefit of best subset of S with weight at most W let A and B be arrays of length W + 1 for w 0 to W do B[w] 0 for k 1 to n do copy array B into array A for w wk to W do if A[w-wk] + bk > A[w] then B[w] A[w-wk] + bk return B[W]

Longest Common Subsequence (LCS) l A subsequence of a sequence/string S is obtained by deleting zero or more symbols from S. For example, the following are some subsequences of “president”: pred, sdn, predent. In other words, the letters of a subsequence of S appear in order in S, but they are not required to be consecutive. l The longest common subsequence problem is to find a maximum length common subsequence between two sequences.

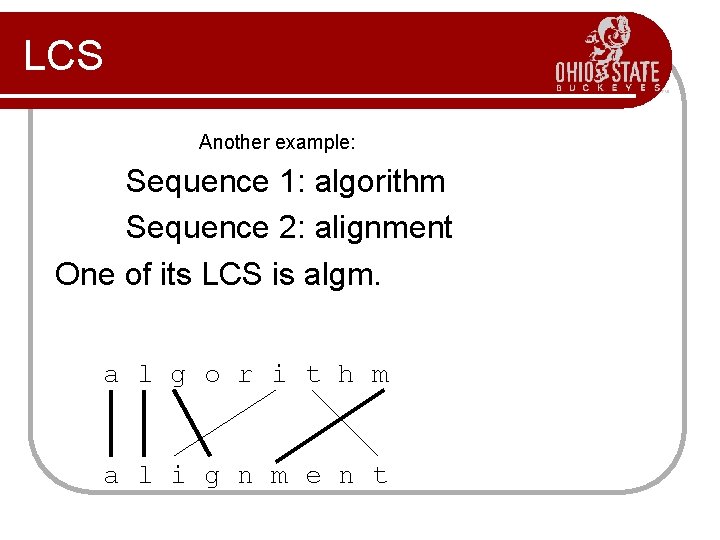
LCS For instance, Sequence 1: president Sequence 2: providence Its LCS is priden. president providence

LCS Another example: Sequence 1: algorithm Sequence 2: alignment One of its LCS is algm. a l g o r i t h m a l i g n m e n t

Naïve Algorithm l For every subsequence of X, check whether it’s a subsequence of Y. l Time: Θ(n 2 m). 2 m subsequences of X to check. l Each subsequence takes Θ(n) time to check: scan Y for first letter, for second, and so on. l

Optimal Substructure Theorem Let Z = z 1, . . . , zk be any LCS of X and Y. 1. If xm = yn, then zk = xm = yn and Zk-1 is an LCS of Xm-1 and Yn-1. 2. If xm yn, then either zk xm and Z is an LCS of Xm-1 and Y. 3. or zk yn and Z is an LCS of X and Yn-1. Notation: prefix Xi = x 1, . . . , xi is the first i letters of X.

Optimal Substructure Theorem Let Z = z 1, . . . , zk be any LCS of X and Y. 1. If xm = yn, then zk = xm = yn and Zk-1 is an LCS of Xm-1 and Yn-1. 2. If xm yn, then either zk xm and Z is an LCS of Xm-1 and Y. 3. or zk yn and Z is an LCS of X and Yn-1. Proof: (case 1: xm = yn) Any sequence Z’ that does not end in xm = yn can be made longer by adding xm = yn to the end. Therefore, (1) longest common subsequence (LCS) Z must end in xm = yn. (2) Zk-1 is a common subsequence of Xm-1 and Yn-1, and (3) there is no longer CS of Xm-1 and Yn-1, or Z would not be an LCS.

Optimal Substructure Theorem Let Z = z 1, . . . , zk be any LCS of X and Y. 1. If xm = yn, then zk = xm = yn and Zk-1 is an LCS of Xm-1 and Yn-1. 2. If xm yn, then either zk xm and Z is an LCS of Xm-1 and Y. 3. or zk yn and Z is an LCS of X and Yn-1. Proof: (case 2: xm yn, and zk xm) Since Z does not end in xm, (1) Z is a common subsequence of Xm-1 and Y, and (2) there is no longer CS of Xm-1 and Y, or Z would not be an LCS.

Recursive Solution Define c[i, j] = length of LCS of Xi and Yj. l We want c[m, n]. l

Recursive Solution c[springtime, printing] c[springtim, printing] [springtim, printin] c[springtime, printin] [springtime, printi] [springt, printing] [springti, printin] [springtim, printi] [springtime, print]

Recursive Solution p • Keep track of c[a, b] in a table of nm entries: • top/down • bottom/up s p r i n g t i m e r i n t i n g

How to compute LCS? Let A=a 1 a 2…am and B=b 1 b 2…bn. l len(i, j): the length of an LCS between a 1 a 2…ai and b 1 b 2…bj l With proper initializations, len(i, j) can be computed as follows. l

LCS Algorithm

Running time and memory: O(mn) and O(mn).

The Backtracking Algorithm procedure Output-LCS(A, prev, i, j) 1. if i = 0 or j = 0 then return 2. if prev(i, j)=” “ then Output-LCS(A, prev, i-1, j-1) Print A[i]; 3. else if prev(i, j)=” “ then Output-LCS(A, prev, i-1, j) 4. else Output-LCS(A, prev, i, j-1)

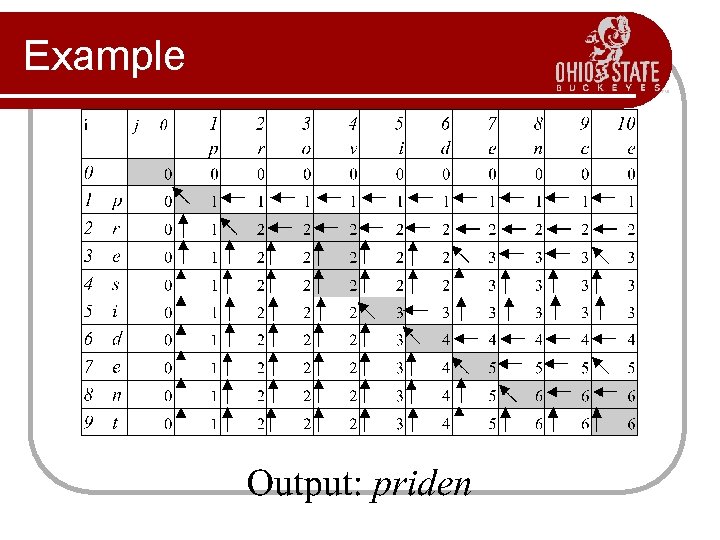
Example

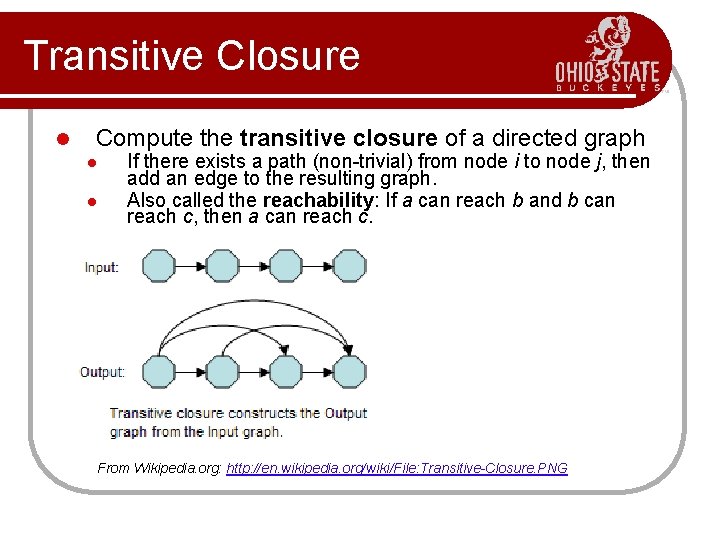
Transitive Closure l Compute the transitive closure of a directed graph l l If there exists a path (non-trivial) from node i to node j, then add an edge to the resulting graph. Also called the reachability: If a can reach b and b can reach c, then a can reach c. From Wikipedia. org: http: //en. wikipedia. org/wiki/File: Transitive-Closure. PNG

Warshall’s Algorithm On the kth iteration, the algorithm determines for every pair of vertices i, j if a path exists from i and j with just vertices 1, …, k allowed as intermediate nodes. l R(k)[i, j] = { R(k-1)[i, j] (path using just 1 , …, k-1) or R(k-1)[i, k] and R(k-1)[k, j] k (path from i to k and from k to j using just 1 , …, k-1) i Initial condition? j

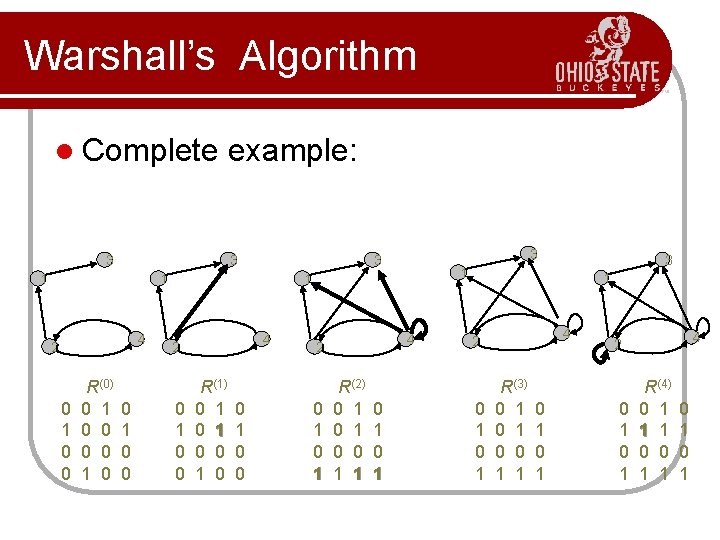
Warshall’s Algorithm Constructs transitive closure T as the last matrix in the sequence of n-by-n matrices R(0), … , R(k), … , R(n) where l R(k)[i, j] = 1 iff there is nontrivial path from i to j with only the first k vertices allowed as intermediate l Note that R(0) = A (adjacency matrix), R(n) = T (transitive closure) l Example: Path’s with only node 1 allowed. l 3 3 1 1 2 4

Warshall’s Algorithm l Complete 3 example: 3 1 4 0 1 0 0 R(0) 0 1 0 0 4 2 0 1 0 0 R(1) 0 1 0 0 4 2 0 1 R(2) 0 1 0 0 1 1 0 1 3 1 1 1 2 3 3 1 4 2 0 1 R(3) 0 1 0 0 1 1 0 1 4 2 0 1 R(4) 0 1 1 1 0 0 1 1 0 1

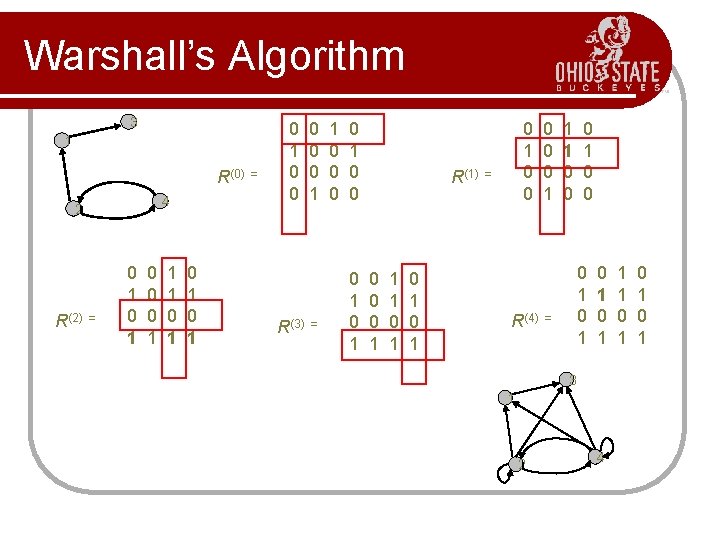
Warshall’s Algorithm 3 1 R(0) 4 2 R(2) = 0 1 0 0 0 1 1 1 0 1 0 1 = 0 1 0 0 R(3) 0 0 0 1 = 1 0 0 0 1 R(1) 0 0 0 1 1 1 0 1 0 1 0 0 = R(4) 0 0 0 1 1 1 0 0 0 1 0 1 = 0 1 3 1 2 4 1 1 0 1 0 1

Warshall’s Algorithm Time efficiency: Θ(n 3) Space efficiency: Matrices can be written over their predecessors (with some care), so it’s Θ(n 2).