Introduction to Algorithms Counting Sort Sorting So Far

Introduction to Algorithms Counting Sort

Sorting So Far • Insertion Sort • Easy to code • Fast on small inputs (less than ~ 50 elements) • Fast on nearly-sorted inputs • O(n 2) worst case • O(n 2) average (equally-likely inputs) case • O(n 2) reverse-sorted case

Sorting So Far • Merge Sort • Divide-and-Conquer • Split array in half • Recursively sort subarrays • Linear-time merge step • O(n lg n) worst case • It does not sort in place

Sorting So Far • Heap Sort • It uses the very useful heap data structure • Complete binary tree • Heap property: parent key > children’s keys • O(n lg n) worst case • It sorts in place

How Fast Can We Sort? • We will provide a lower bound, then beat it • How do you suppose we’ll beat it? • First, an observation: all of the sorting algorithms so far are comparison sorts • The only operation used to gain ordering information about a sequence is the pairwise comparison of two elements • Theorem: all comparison sorts are Ω(n lg n)

Decision Trees 5 7 3 5 73 37 35 35 7

Decision Trees • Decision trees provide an abstraction of comparison sorts A decision tree represents the comparisons made by a comparison sort. • What do the leaves represent? • How many leaves must there be?

Decision Trees • Decision trees can model comparison sorts • For a given algorithm: • One tree for each n • Tree paths are all possible execution traces • What’s the longest path in a decision tree for insertion sort? • For merge sort? • What is the asymptotic height of any decision tree for sorting n elements? Answer: Ω(n lg n) (Now let’s prove it…)

A Lower Bound for Comparison Sorts • Thus the time to comparison sort n elements is Ω(n lg n) • Corollary: Heapsort and Mergesort are asymptotically optimal comparison sorts • But the name of this lecture is “Sorting in linear time”! • How can we do better than Ω(n lg n)?

Sorting in Linear Time • Counting Sort • No comparisons between elements ! • But…depends on assumption about the numbers being sorted • Basic Idea • For each input element x, • determine the number of elements less than or equal to x • For each integer i (0 ≤ i ≤ k), count how many elements whose • values are i Then we know how many elements are less than or equal to i • Algorithm Storage • A[1. . n]: input elements • B[1. . n]: sorted elements • C[0. . k]: hold the number of elements less than or equal to i

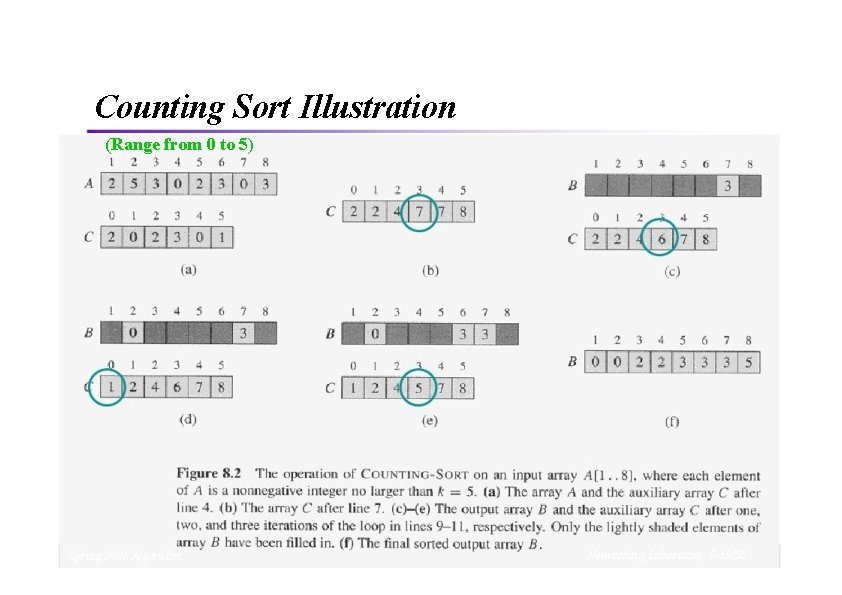
Counting Sort Illustration (Range from 0 to 5) Spring 2006 Algorithm Networking Laboratory 5 -15/55

Counting Sort Illustration A 2 5 3 0 2 3 0 3 B C B 0 0 2 3 3 C 0 2 3 5 7 8 B 0 0 2 2 3 3 3 8 C 0 2 3 4 7 7 0 1 2 4 5 7 8 B 0 0 C 3 3 2 3 3 3 0 2 3 4 7 8 B C 0 3 3 1 2 3 5 7 8 B 0 0 C 2 2 3 3 3 8 0 2 32 4 7 7

Counting Sort Θ(k) Θ(n) Θ(n+k)

Counting Sort • Total time: O(n + k) • Usually, k = O(n) • Thus counting sort runs in O(n) time • But sorting is Ω(n lg n)! • No contradiction • This is not a comparison sort • In fact, there are no comparisons at all ! • Notice that this algorithm is stable

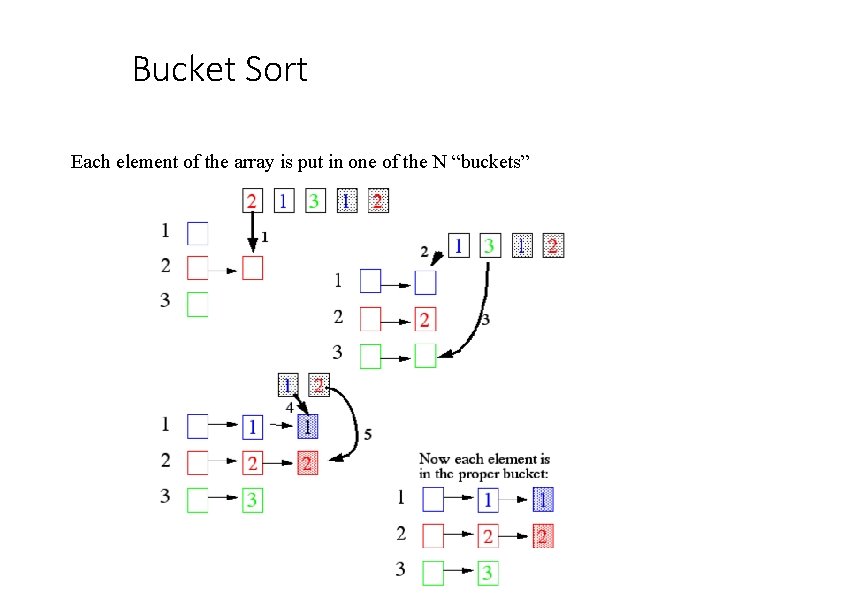
Bucket Sort • Bucket sort • Assumption: the keys are in the range [0, N) • Basic idea: 1. Create N linked lists (buckets) to divide interval [0, N) into subintervals of size 1 2. Add each input element to appropriate bucket 3. Concatenate the buckets • Expected total time is O(n + N), with n = size of original sequence • if N is O(n) sorting algorithm in O(n) !

Bucket Sort Each element of the array is put in one of the N “buckets”

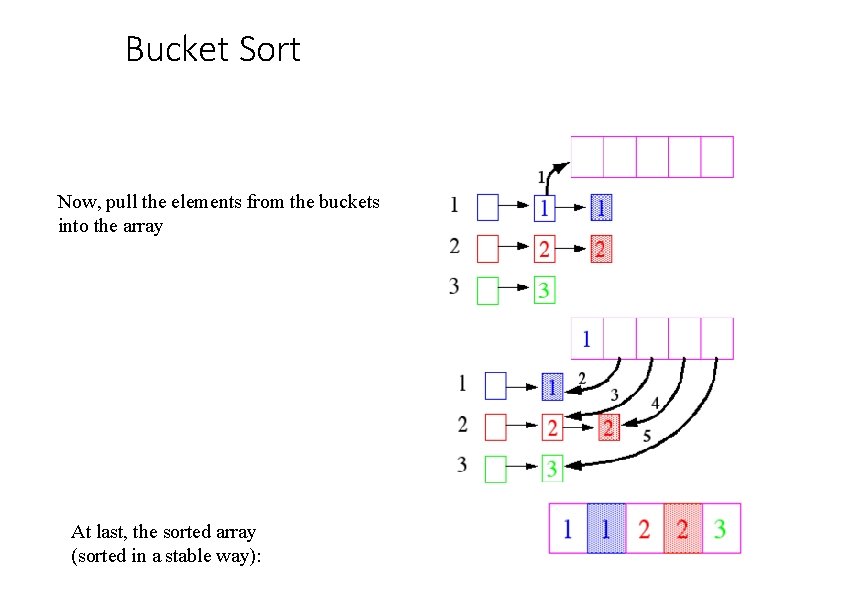
Bucket Sort Now, pull the elements from the buckets into the array At last, the sorted array (sorted in a stable way):

Does it Work for Real Numbers? • What if keys are not integers? • Assumption: input is n reals from [0, 1) • Basic idea: • Create N linked lists (buckets) to divide interval [0, 1) into subintervals of size 1/N • Add each input element to appropriate bucket and sort buckets with insertion sort • Uniform input distribution O(1) bucket size • Therefore the expected total time is O(n) • Distribution of keys in buckets similar with …. ?

Radix Sort • How did IBM get rich originally? • Answer: punched card readers for census tabulation in early 1900’s. • In particular, a card sorter that could sort cards into different bins • Each column can be punched in 12 places • (Decimal digits use only 10 places!) • Problem: only one column can be sorted on at a time

Radix Sort • Intuitively, you might sort on the most significant digit, then the second most significant, etc. • Problem: lots of intermediate piles of cards to keep track of • Key idea: sort the least significant digit first Radix. Sort(A, d) for i=1 to d Stable. Sort(A) on digit i

Radix Sort • Can we prove it will work? • Inductive argument: • Assume lower-order digits {j: j<i}are sorted • Show that sorting next digit i leaves array correctly sorted • If two digits at position i are different, ordering numbers by that digit is correct (lowerorder digits irrelevant) • If they are the same, numbers are already sorted on the lower-order digits. Since we use a stable sort, the numbers stay in the right order

Radix Sort • What sort will we use to sort on digits? • Bucket sort is a good choice: • Sort n numbers on digits that range from 1. . N • Time: O(n + N) • Each pass over n numbers with d digits takes time O(n+k), so total time O(dn+dk) • When d is constant and k=O(n), takes O(n) time

Radix Sort Example • Problem: sort 1 million 64 -bit numbers • Treat as four-digit radix 216 numbers • Can sort in just four passes with radix sort! • Running time: 4( 1 million + 216 ) 4 million operations • Compare with typical O(n lg n) comparison sort • Requires approx lg n = 20 operations per number being sorted • Total running time 20 million operations

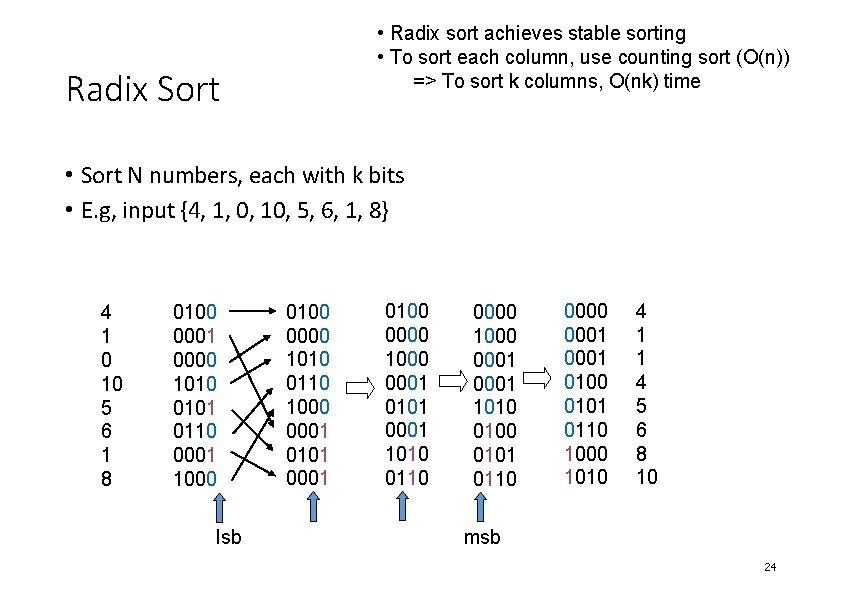
• Radix sort achieves stable sorting • To sort each column, use counting sort (O(n)) => To sort k columns, O(nk) time Radix Sort • Sort N numbers, each with k bits • E. g, input {4, 1, 0, 10, 5, 6, 1, 8} 4 1 0 10 5 6 1 8 0100 0001 0000 1010 0101 0110 0001 1000 lsb 0100 0000 1010 0110 1000 0001 0101 0001 0100 0000 1000 0001 0101 0001 1010 0110 0000 1000 0001 1010 0101 0110 0001 0100 0101 0110 1000 1010 4 1 1 4 5 6 8 10 msb 24

Radix Sort • In general, radix sort based on bucket sort is • Asymptotically fast (i. e. , O(n)) • Simple to code • A good choice • Can radix sort be used on floating-point numbers?

Summary: Radix Sort • Radix sort: • Assumption: input has d digits ranging from 0 to k • Basic idea: • Sort elements by digit starting with least significant • Use a stable sort (like bucket sort) for each stage • Each pass over n numbers with 1 digit takes time O(n+k), so total time O(dn+dk) • When d is constant and k=O(n), takes O(n) time • Fast, Stable, Simple • Doesn’t sort in place