Introduction to Algorithms Algorithm Efficiency No single solution

Introduction to Algorithms

Algorithm Efficiency No single solution exists for any problem Multiple solutions or algorithms exist Algorithms differ in their order of magnitude w. r. t space and time Brassard and Bratley coined the term Algorithmics – “the systematic study of the fundamental techniques used to design and analyze efficient algorithms” 9/29/2020 Department of Information Technology , TCE 2

Algorithm Efficiency is a function of the number of instructions it contains. Function is Linear if there are no loops or no recursions - Depends on the speed of computer - Not a factor in the overall efficiency of program - Very meager, can just be ignored - Loops or recursions used in the function contribute more to its performance. - This study of Algorithm Efficiency is focused towards loops/recursions 9/29/2020 Department of Information Technology , TCE 3

Algorithm Efficiency Function of number of elements to be processed f(n) = efficiency Linear Loops - How many times the body of the loop is repeated for (i=0; i< 1000; i++) … code …. 1000 times Number of iterations is directly proportional to the loop factor Efficiency is directly proportional to the number of iterations f(n) = n 9/29/2020 Department of Information Technology , TCE 4

Algorithm Efficiency Linear Loops - How many times the body of the loop is repeated for (i=0; i< 1000; i+=2) … code …. 500 times Number of iterations is half the loop factor Efficiency is directly proportional to the number of iterations f(n) = n/2 9/29/2020 Department of Information Technology , TCE Plotting the points gives you straight line. So Linear loops 5

Algorithm Efficiency Logarthmic Loops - the controlling variable is either multiplied or divided in each iteration for (i=1; i< 1000; i *= 2) for (i=1000; i > 0; i /= 2) … code … How many iterations that each code takes? Use table to find this f(n) = log n 9/29/2020 Department of Information Technology , TCE 6

Algorithm Efficiency Nested Loops - How many iterations each loop completes to be determined - Product of number of iterations of inner loop and outer loop for (i=0; i< 10; i++) for (j=0; j < 10; j *=2) … code …. 10 * log 10 f(n) = n log n 9/29/2020 Department of Information Technology , TCE 7

Algorithm Efficiency Quadratic Loops - How many iterations each loop completes to be determined - Product of number of iterations of inner loop and outer loop - Number of times the inner loop executes is the same as the outer loop for (i=0; i< 10; i++) for (j=0; j < 10; j++) … code …. 10 * 10 times f(n) = n 2 9/29/2020 Department of Information Technology , TCE 8

Algorithm Efficiency Dependant Quadratic Loops for (i=0; i< 10; i++) for (j=0; j < i ; j++) … code …. - Number of iterations of the inner loop depends on the outer loop - Outer loop executes ‘n’ times - Inner loop depends on the outer loop once for first iteration, twice for second iteration, and so on Inner loop iterates 1 + 2 + 3 + …. + 10 = 55 Average of this gives 55/10 = 5. 5 Roughly it is equivalent to (n+1)/2 f(n) = n ( (n+1) / 2 ) 9/29/2020 Department of Information Technology , TCE 9

Quiz Efficiency of following Algorithms Sum of ‘n’ numbers Addition of two matrices Multiplication of two matrices Fibonacci series Factorial of a number Rank the following n, n 2 , log n, n log n 9/29/2020 Department of Information Technology , TCE 10

Algorithm Analysis Best Case − Minimum time required for program execution. Average Case − Average time required for program execution. Worst Case − Maximum time required for program execution. Ex 1 : Linear Search Ex 2: Binary Search 3, 9, 12, 6, 15, 33, 39, 45, 27 3, 6, 9, 12, 15, 27, 33, 39, 45 search(3) - best case search (? ) – best case search(15) – average case search (? ) – average case search(27) – worst case search (? ) – worst case 9/29/2020 Department of Information Technology , TCE 11

Asymptotic Notations Big Oh O - upper bound of algorithm worst case time complexity Omega Ω - lower bound of algorithm best case time complexity Theta Θ – both lower and upper bound of algorithm average case time complexity 9/29/2020 Department of Information Technology , TCE 12

Algorithmic Notations Big O Notation Time taken for a function to complete its execution is visible if ‘n’ is very large Not interested in the complete measure of efficiency Interested only in the factor that determines the magnitude This factor is the Big-O , “on the order of” - O(n) is “on the order of n” If the algorithm is quadratic, its efficiency is O(n 2) 9/29/2020 Department of Information Technology , TCE 13

Algorithmic Notations Big O Notation Steps for big-O analysis 1. Suppose f(n) = n (n+1) /2 n 2 /2 + n/2 2. Remove co-efficients n 2 + n 3. Remove smaller factors n 2 So, O(f(n)) = O(n 2) 9/29/2020 Department of Information Technology , TCE 14

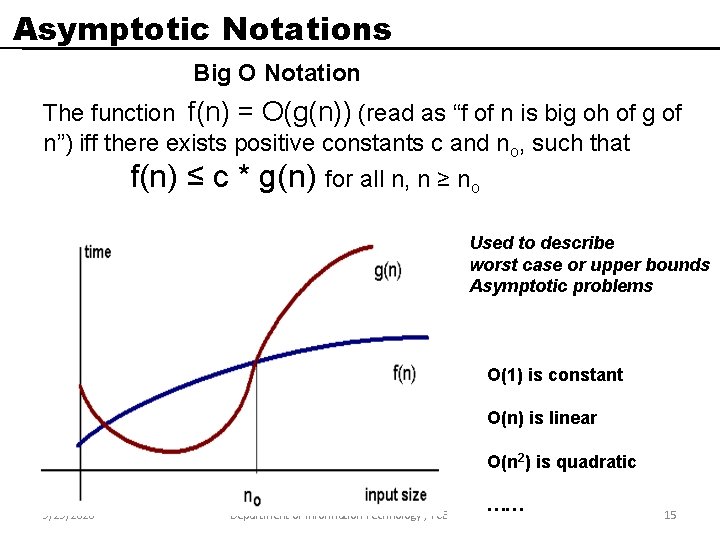
Asymptotic Notations Big O Notation The function f(n) = O(g(n)) (read as “f of n is big oh of g of n”) iff there exists positive constants c and no, such that f(n) ≤ c * g(n) for all n, n ≥ no Used to describe worst case or upper bounds Asymptotic problems O(1) is constant O(n) is linear O(n 2) is quadratic 9/29/2020 Department of Information Technology , TCE …… 15

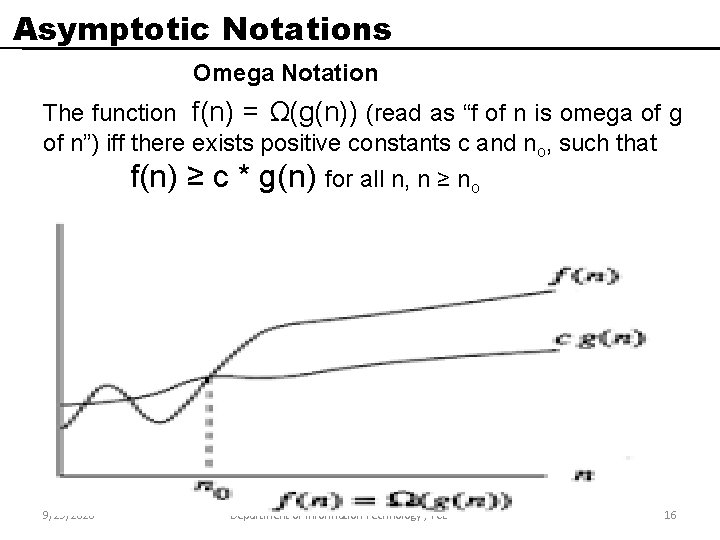
Asymptotic Notations Omega Notation The function f(n) = Ω(g(n)) (read as “f of n is omega of g of n”) iff there exists positive constants c and no, such that f(n) ≥ c * g(n) for all n, n ≥ no 9/29/2020 Department of Information Technology , TCE 16

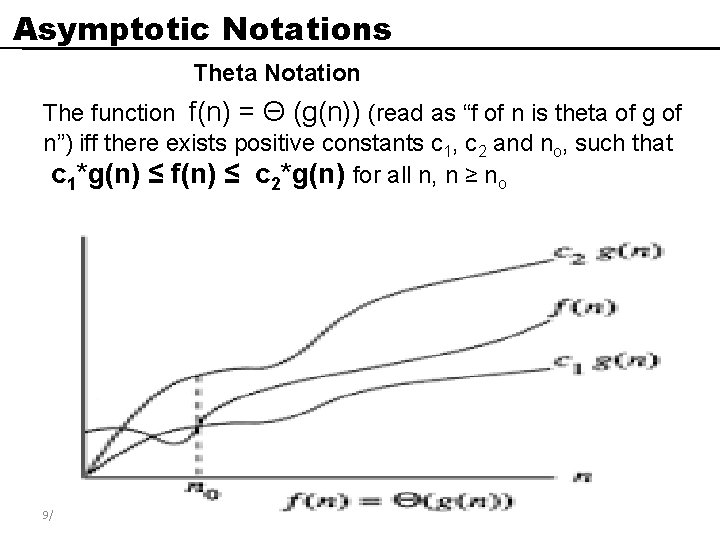
Asymptotic Notations Theta Notation The function f(n) = Θ (g(n)) (read as “f of n is theta of g of n”) iff there exists positive constants c 1, c 2 and no, such that c 1*g(n) ≤ f(n) ≤ c 2*g(n) for all n, n ≥ no 9/29/2020 Department of Information Technology , TCE 17

Asymptotic complexity Space Complexity of an algorithm is total space taken by the algorithm with respect to the input size. Space complexity includes both temporary space and space used by input. Time complexity of an algorithm quantifies the amount of time taken by an algorithm to run as a function of the length of the input. The time complexity of an algorithm is commonly expressed using Big O notation When expressed this way, the time complexity is said to be described asymptotically, i. e. , as the input size goes to infinity. For example, if the time required by an algorithm on all inputs of size n is at most 5 n 3 + 3 n for any n (bigger than some n 0), the asymptotic time complexity is O(n 3). 9/29/2020 Department of Information Technology , TCE 18

Time and Space complexity function sum(a, n) s = 0; for i = 1 to n do s = s + a[i]; return s; Time Complexity 1 time n+1 times n times 1 time 1 + n+1 + n + 1 = 2 n + 3 So O(n) Space Complexity integers - 3 for the variables i, n, s array size - n So, n + 3 integers 9/29/2020 Department of Information Technology , TCE 19

Time complexity int fun(int n) { int count = 0; for (int i = n; i > 0; i /= 2) for (int j = 0; j < i; j++) count += 1; return count; } A. O(n 2) B. O(n log n) C. O(n) D. O(n log n) Its dependant quadratic loop T(n) = n + n/2 + n/4 + …. . Ans : C 9/29/2020 Department of Information Technology , TCE 20

Time complexity int fun(int n) { int count = 0; for (int i = 0; i < n; i++) for (int j = i; j > 0; j--) count = count + 1; return count; } A. Theta(n 2) B. Theta(n) C. Theta(n log n) D. Theta(n log n) Ans : A 9/29/2020 Department of Information Technology , TCE 21

Time complexity Which of the given options provides the increasing order of asymptotic complexity of functions f 1, f 2, f 3 and f 4? A. f 3, f 2, f 4, f 1(n) = 2^n f 2(n) = n^(3/2) B. f 3, f 2, f 1, f 4 f 3(n) = n. Logn C. f 2, f 3, f 1, f 4(n) = n^(Logn) D. f 2, f 3, f 4, f 1 Ans : A 9/29/2020 Department of Information Technology , TCE 22