Introduction to 3 D Graphics Lecture 4 Scenes

Introduction to 3 D Graphics Lecture 4: Scenes and Scene Graphs Anthony Steed University College London

No More Spheres!

Overview n Polygons – Representation – Intersection n Polyhedra – Face sets – Winged edge n Scene graphs

Polygons n A polygon (face) Q is defined by a series of points n The points are must be co-planar n 3 points define a plane, but a 4 th point need not lie on that plane

Types of Polygon n Simple - Concave, Convex n Complex We like simple, concave polygons since they are easy to break into triangles

Equation of a Plane n a, b, c and d are constants that define a unique plane and x, y and z form a vector P.

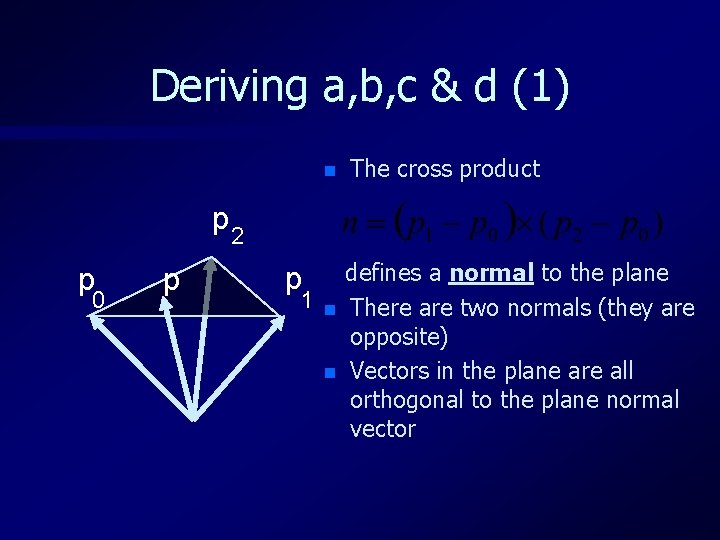
Deriving a, b, c & d (1) n The cross product p 2 p 0 p p 1 n n defines a normal to the plane There are two normals (they are opposite) Vectors in the plane are all orthogonal to the plane normal vector

Deriving a, b, c & d (2) n So p-p 0 is normal to n therefore n But if n = (n 1, n 2, n 3) – a= n 1 b= n 2 c= n 3 (n. p) – d = n. p 0 = n 1*x 0 + n 2*y 0 + n 3*z 0

Half-Space n A plane cuts space into 2 half-spaces Define n If l(p) =0 n If l(p) > 0 n If l(p) <0 n – point on plane – point in positive half-space – point in negative half-space

Outline of Polygon Ray Casting n Three steps – Does the ray intersect the plane of the polygon? n i. e. is the ray not orthogonal to the plane normal – Intersect ray with plane – Test whether intersection point lies within polygon on the plane

Does the ray intersect the plane? Ray eq. is p 0 + t. d n Plane eq. is n. (x, y, z) = k n n Then test is n. d !=0

Where does it intersect? n Substitute line equation into plane equation n Solve for t n Find pi

Is this point inside the polygon? n Many tests are possible – Winding number (can be done in 3 D) – Infinite ray test (done in 2 D)

Winding Number Test n Sum the angle subtended by the vertices p 2 1 p 1 n-1 pn-1

Inside and Outside n n Not just draw (stroke, fill) For closed Shapes – Hit test - inside or outside based on a winding rules (non-zero or even-odd)

Counting Edge Crosses n Draw a line from the test point to the outside – Count +1 if you cross an edge in an anti-clockwise sense – Count -1 if you cross and edge in a clockwise sense -1 +1

Overview n Polygons – Representation – Intersection n Polyhedra – Face sets – Winged edge n Scene graphs

Polyhedra n Polygons are often grouped together to form polyhedra – Each edge connects 2 vertices and is the join between two polygons – Each vertex joins 3 edges – No faces intersect n V-E+F=2 – For cubes, tetrahedra, cows etc. . .

Example Polhedron v 4 e 7 n v 3 n n e 9 e 5 e 4 vo e 6 v 5 e 3 e 1 e 8 n n v 2 n e 2 v 1 n F 0=v 0 v 1 v 4 F 1=v 5 v 3 v 2 F 2=v 1 v 2 v 3 v 4 F 3=v 0 v 4 v 3 v 5 F 4=v 0 v 5 v 2 v 1 V=6, F=5, E=9 V-E+F=2

Representing Polyhedron (1) n Exhaustive (array of vertex lists) – faces[1] = (x 0, y 0, z 0), (x 1, y 1, z 1), (x 3, y 3, z 3) – faces[2] = (x 2, y 2, z 2), (x 0, y 0, z 0), (x 3, y 3, z 3) – etc …. n Very wasteful since same vertex appears at 3(or more) points in the list – Is used a lot though!

Representing Polyhedron (2) n Indexed Face set Vertex array n Face array (list of indices into vertex array) n – vertices[0] = (x 0, y 0, z 0) – vertices[1]=(x 1, y 1, z 1) – etc … – faces[0] = 0, 2, 1 – faces[1]=2, 3, 1 – etc. . .

Vertex order matters n v 4 v 3 n n v 5 vo v 2 v 1 n Polygon v 0, v 1, v 4 is NOT equal to v 0, v 4, v 1 The normal point in different directions Usually a polygon is only visible from points in its positive half-space This is known as back-face culling

Representing Polyhedron (3) n Even Indexed face set wastes space – Each face edge is represented twice n Winged edge data structure solves this – vertex list – edge list (vertex pairs) – face list (edge lists)

The Edge List Structure NCCW( e) P CW( e ) n P V( e) NF ace( e ) e P F ace( e) N V( e) NCW( e ) P CCW( e) Edge contains – – – – Next edge CW Next edge CCW Prev edge CCW Next face Prev face Next vertex Prev vertex

Advantages of Winged Edge n Simple searches are rapid – – – n find all edges find all faces of a vertex etc… Complex operations – – polygon splitting is easy (LOD) silhouette finding potentially efficient for hardware etc…

Building the WE Build indexed face set n Traverse each face in CCW order building edges n – label p and n vertices, p and n faces and link previous CCW edge we fill in next CCW on next edge in this face n we fill in next CW and prev CW when traversing the adjacent face. n

Overview n Polygons – Representation – Intersection n Polyhedra – Face sets – Winged edge n Scene graphs

Concept of Scene Graph Objects placed relative to one another n Objects made of similar components n Directed acyclic graph n root

Use for Animation/Modelling H F E U S B

n One object has a local transformation relative to its parent – shoulder is translation (0 1 0) from base – upper arm is translation (0 3 0) from shoulder – elbow is translation (0 3 0) from upper arm – fore arm is rotation Z by -90 then translation (0 2 0)

Rendering Traverse Must get object definitions in WC before passing to camera n For object under Base n – p. B is in WC “inherit” matrices down stack n So for object under shoulder n – p. SB is in WC – (p. S is in base coordinates)

In general n On traverse – “push” on graph descend – “pop” on graph ascend n Combined matrix is current transform (CTM)

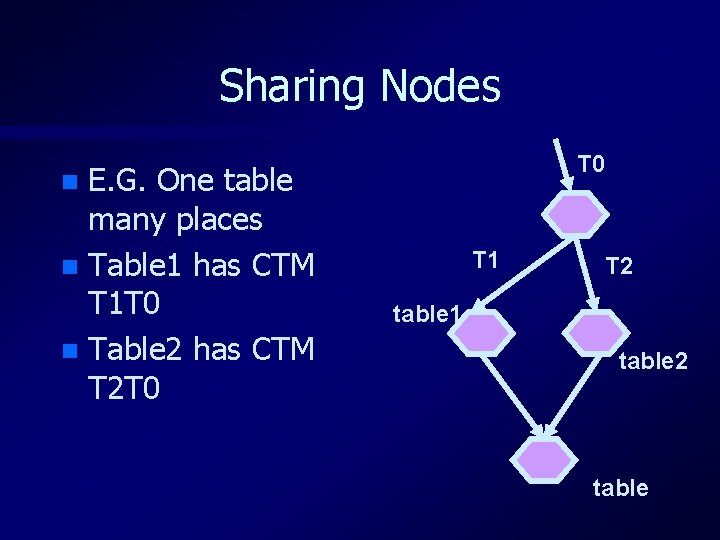
Sharing Nodes E. G. One table many places n Table 1 has CTM T 1 T 0 n Table 2 has CTM T 2 T 0 n T 1 T 2 table 1 table 2 table

Spherical Coordinates n Represent a point on a using two angles and . Where r = length(x, y, z) Z P (x, y, z) Y j O q Q X Q is projection of P onto XY plane is angle between X axis and OQ is angle between OP and Z axis

Spherical Coordinates Length OQ = r sin( ) n So n – x = r sin( )cos( ) – y = r sin( ) – z = r cos( )

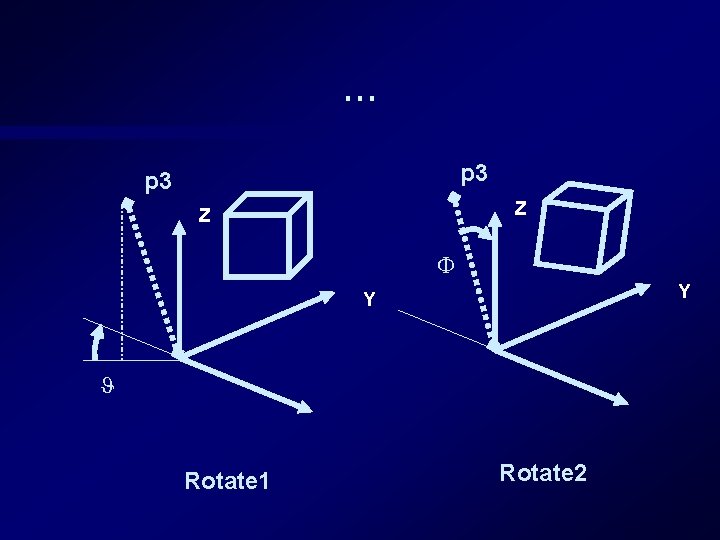
Rotation About an Arbitrary Axis Z p 2 Y O p 1 X

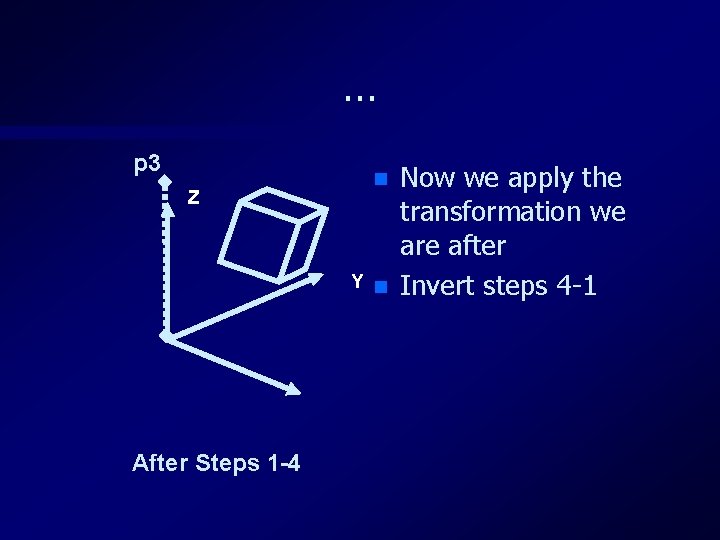
… 1. Translate p 1 so it is at the origin 2. Let p 3 = p 2 -p 1 (new position of p 2) find spherical co-ordinate of p 3 (r, , ) 3. Rotate about Z by - to bring p 3 into ZX plane 4. Rotate about Y by - to bring p 3 onto Z axis 5. Now rotate about Z by 6. Invert steps 4 -1

… Z p 3 p 2 Z Y Y O p 1 Start O Translate

… p 3 Z Z Y Y Rotate 1 Rotate 2

… p 3 Z n Y n After Steps 1 -4 Now we apply the transformation we are after Invert steps 4 -1

Summary n Established a set of techniques for describing scenes made of polygons – Particularly the roles of local-coordinates, which form the modelling matrix stack in Open. Gl n Described how to ray-cast these shapes – The mathematics of this will be crucial when we turn to projection next week.