Introduction to 2 D Projectile Motion Projectile Motion









- Slides: 25

Introduction to 2 D Projectile Motion

Projectile Motion An example of 2 -dimensional motion. n Something is fired, thrown, shot, or hurled near the earth’s surface. n Horizontal velocity is constant. n Vertical velocity is accelerated. n Air resistance is ignored. n

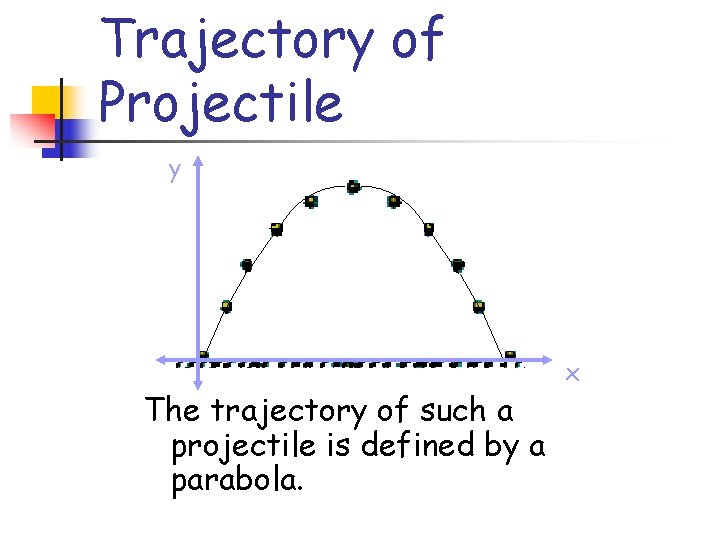
Trajectory of Projectile y x This projectile is launched an an angle and rises to a peak before falling back down.

Trajectory of Projectile y The trajectory of such a projectile is defined by a parabola. x

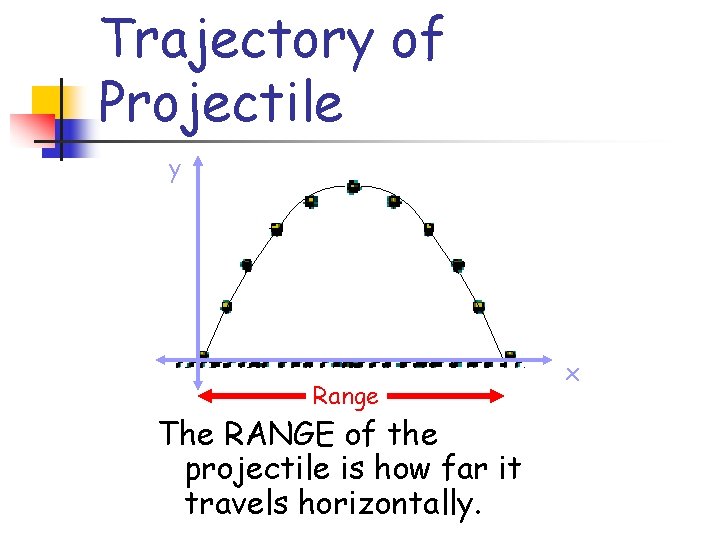
Trajectory of Projectile y Range The RANGE of the projectile is how far it travels horizontally. x

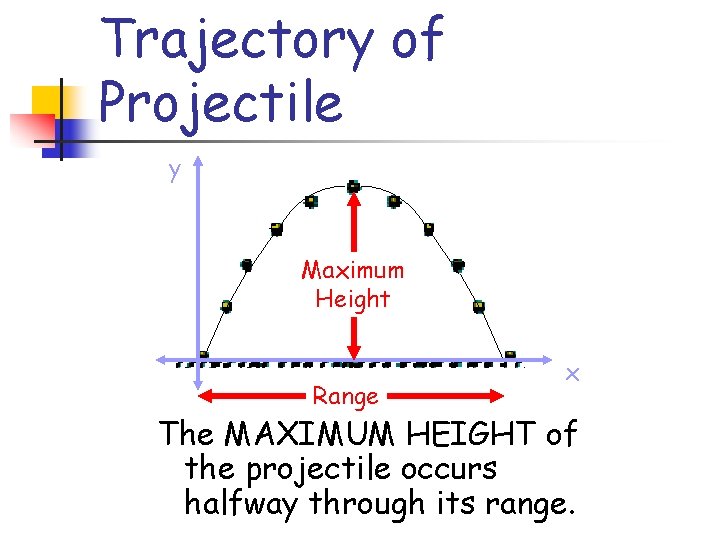
Trajectory of Projectile y Maximum Height Range x The MAXIMUM HEIGHT of the projectile occurs halfway through its range.

Trajectory of Projectile y g g g x Acceleration points down at 9. 8 m/s 2 for the entire trajectory.

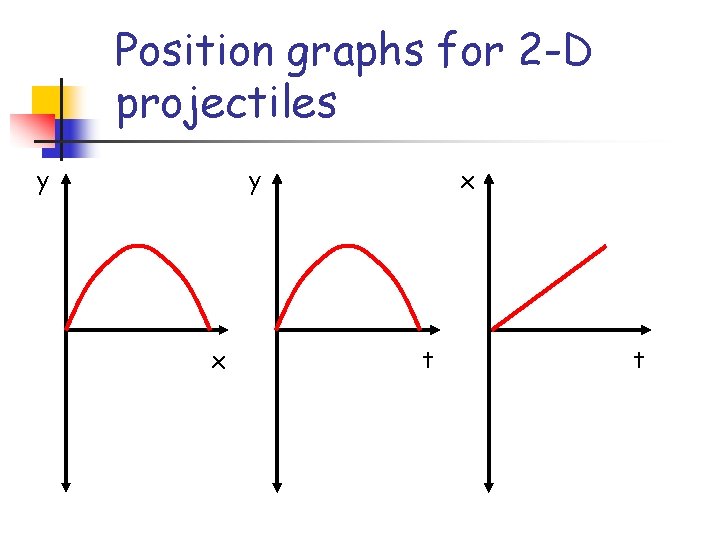
Position graphs for 2 -D projectiles y y x x t t

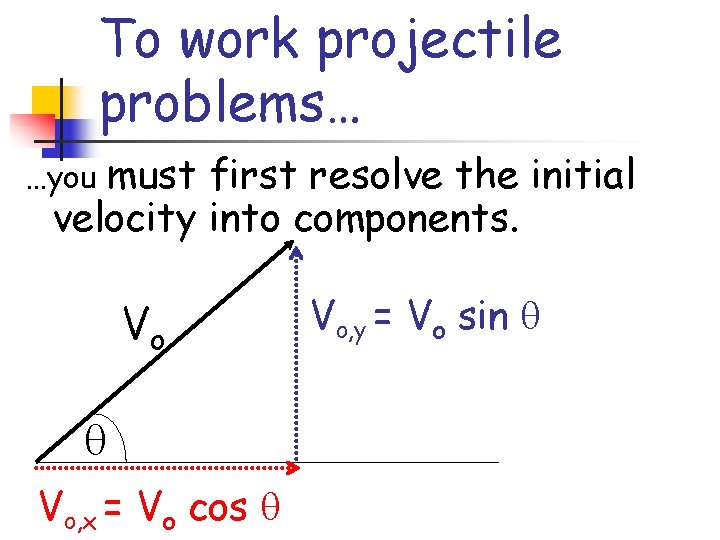
To work projectile problems… must first resolve the initial velocity into components. …you Vo Vo, x = Vo cos Vo, y = Vo sin

Trajectory of Projectile y v v vo v vf x Velocity is tangent to the path for the entire trajectory.

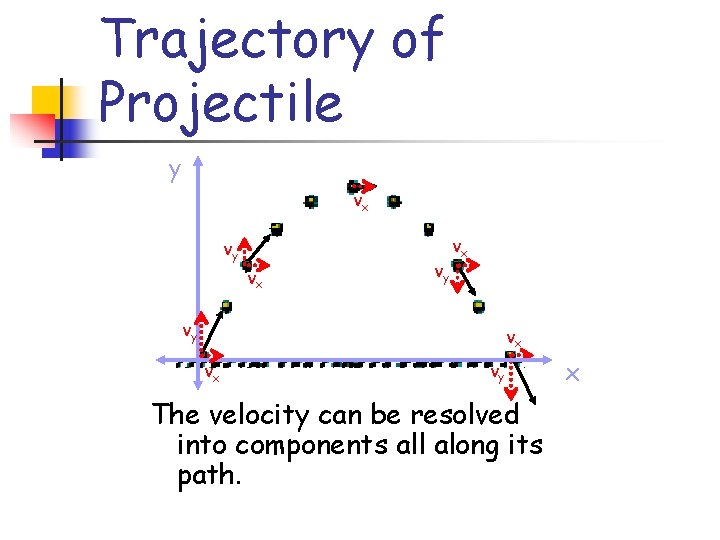
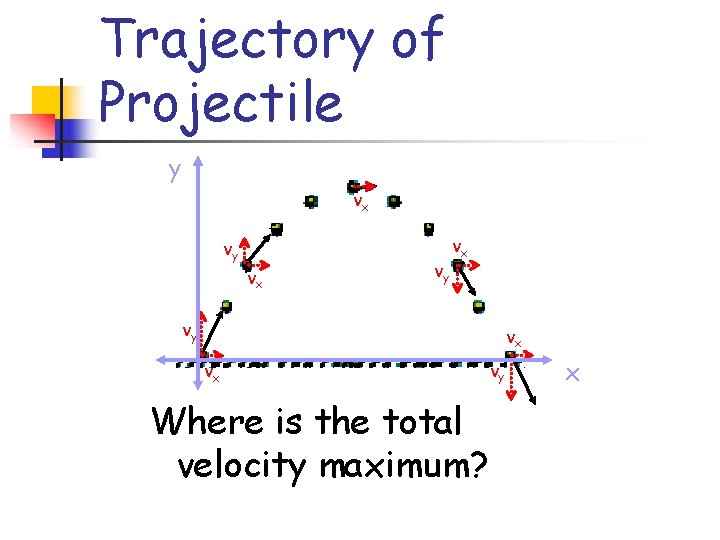
Trajectory of Projectile y vx vy vx vx vy The velocity can be resolved into components all along its path. x

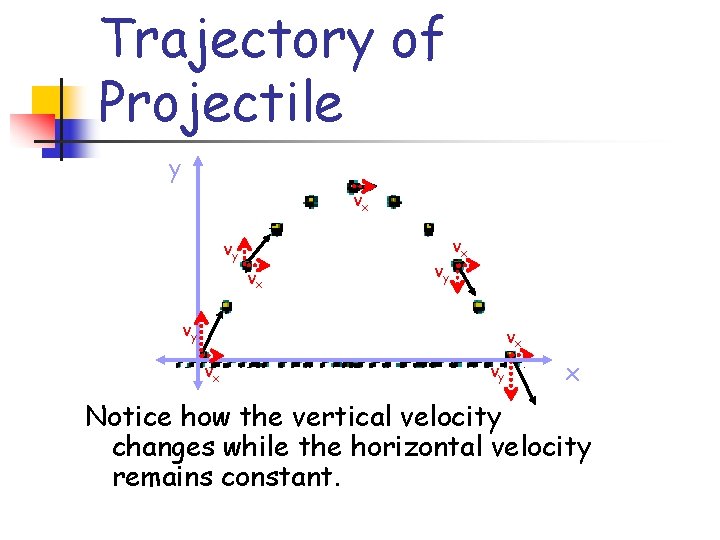
Trajectory of Projectile y vx vy vx vx vy x Notice how the vertical velocity changes while the horizontal velocity remains constant.

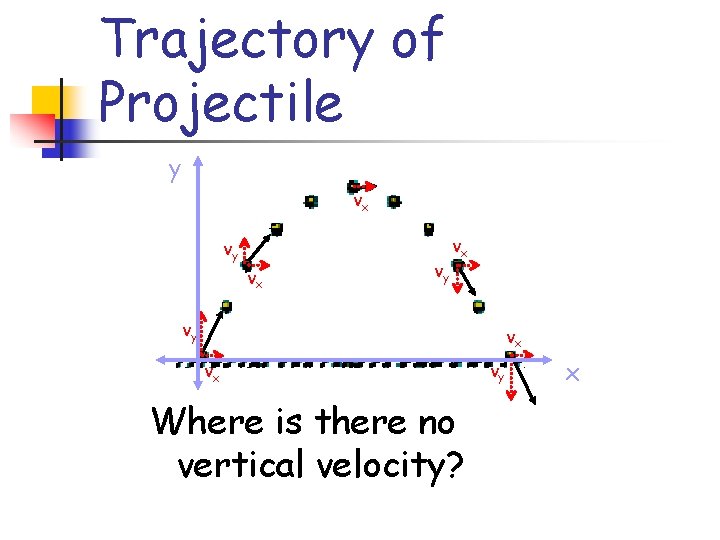
Trajectory of Projectile y vx vy vx vx Where is there no vertical velocity? vy x

Trajectory of Projectile y vx vy vx vx Where is the total velocity maximum? vy x

2 D Motion n Resolve vector into components. n Position, velocity or acceleration Work as two one-dimensional problems. n Each dimension can obey different equations of motion. n

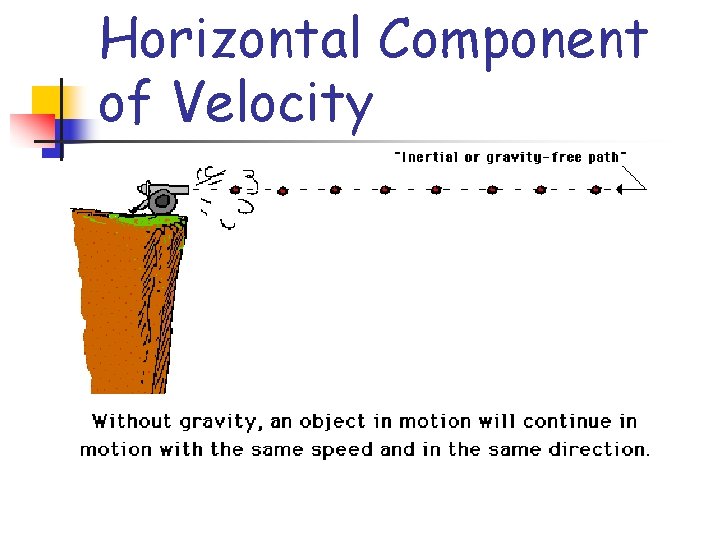
Horizontal Component of Velocity Is constant n Not accelerated n Not influence by gravity n Follows equation: x = Vo, xt n

Horizontal Component of Velocity

Vertical Component of Velocity Undergoes accelerated motion n Accelerated by gravity (9. 8 m/s 2 down) n Vy = Vo, y - gt n y = yo + Vo, yt - 1/2 gt 2 n Vy 2 = Vo, y 2 - 2 g(y – yo) n

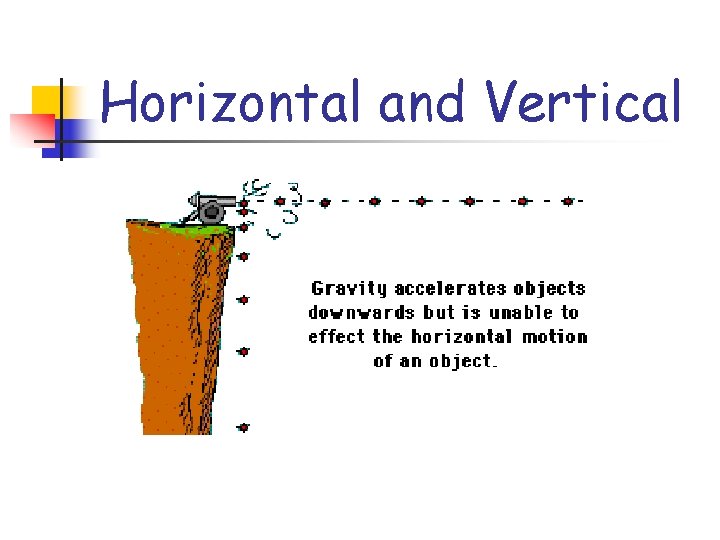
Horizontal and Vertical

Horizontal and Vertical

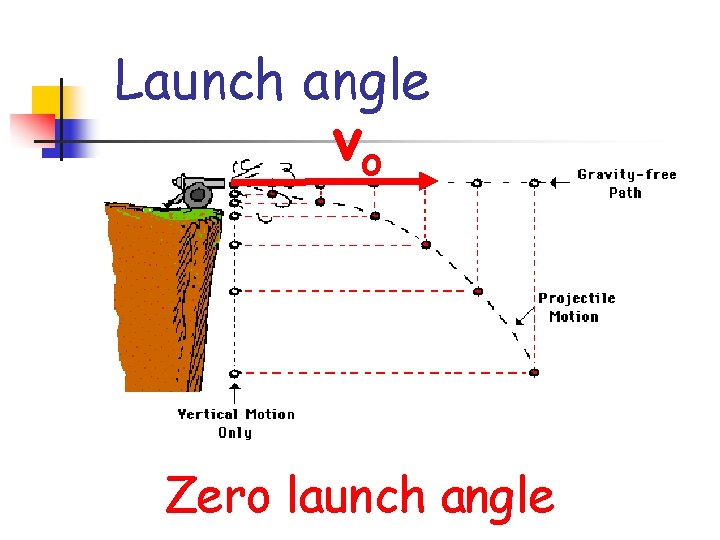
Launch angle vo Zero launch angle

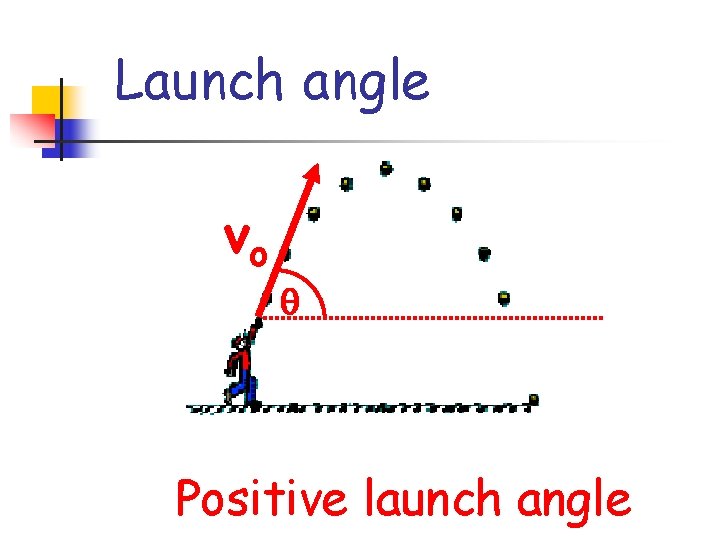
Launch angle vo Positive launch angle

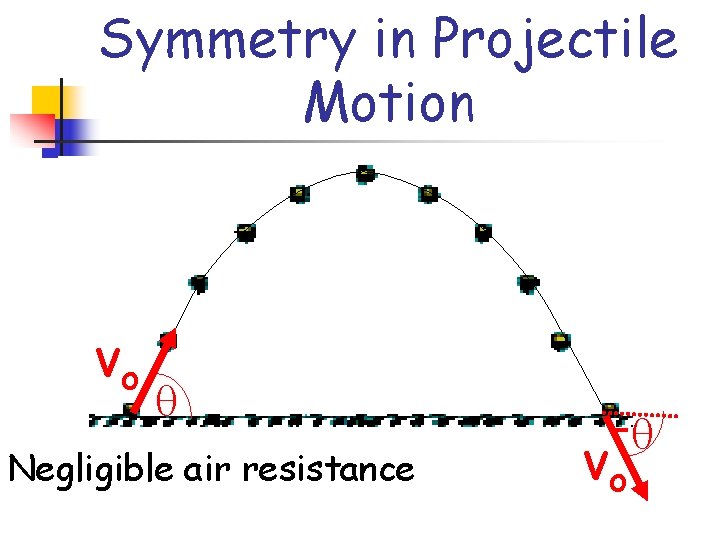
Symmetry in Projectile Motion Launch and Landing Velocity Negligible air resistance Projectile fired over level ground - vo vo

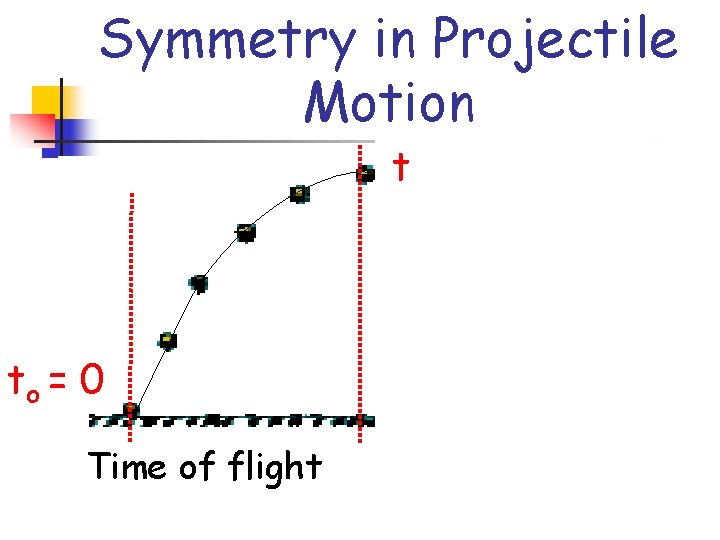
Symmetry in Projectile Motion t to = 0 Time of flight

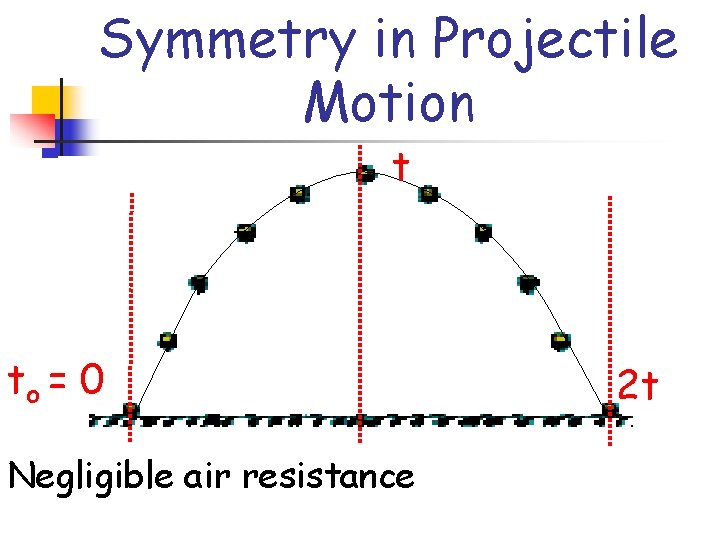
Symmetry in Projectile Motion t to = 0 Time of Projectile fired over level ground Negligible airflight resistance 2 t