Introduction This chapter focuses on using some numerical

Introduction • This chapter focuses on using some numerical methods to solve problems • We will look at finding the region where a root lies • We will learn what iteration is and how it solves equations

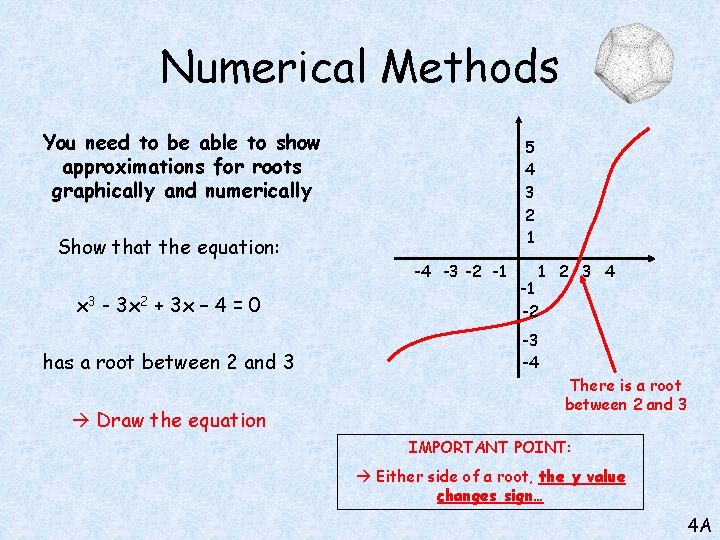
Numerical Methods You need to be able to show approximations for roots graphically and numerically Show that the equation: x 3 - 3 x 2 + 3 x – 4 = 0 has a root between 2 and 3 Draw the equation 5 4 3 2 1 -4 -3 -2 -1 1 2 3 4 -1 -2 -3 -4 There is a root between 2 and 3 IMPORTANT POINT: Either side of a root, the y value changes sign… 4 A

Numerical Methods You need to be able to show approximations for roots graphically and numerically Show numerically that the equation: f(x) = ex + 2 x - 3 f(0. 5) = e 0. 5 + 2(0. 5) - 3 f(0. 5) =-0. 351… ex + 2 x – 3 = 0 has a root between x = 0. 5 and x = 0. 6… f(0. 6) = e 0. 6 + 2(0. 6) - 3 f(0. 6) = 0. 022 The sign has swapped so the function has passed through the x-axis Hence, there is a root between x = 0. 5 and x = 0. 6 4 A

Numerical Methods You need to be able to show approximations for roots graphically and numerically y = 1/ x In General, if there is an interval where f(x) changes sign, there is a root in that interval. The only exception is if there is a discontinuity in f(x), such as on the graph y = 1/x On this graph, there is a missing value where the sign change would take place 4 A

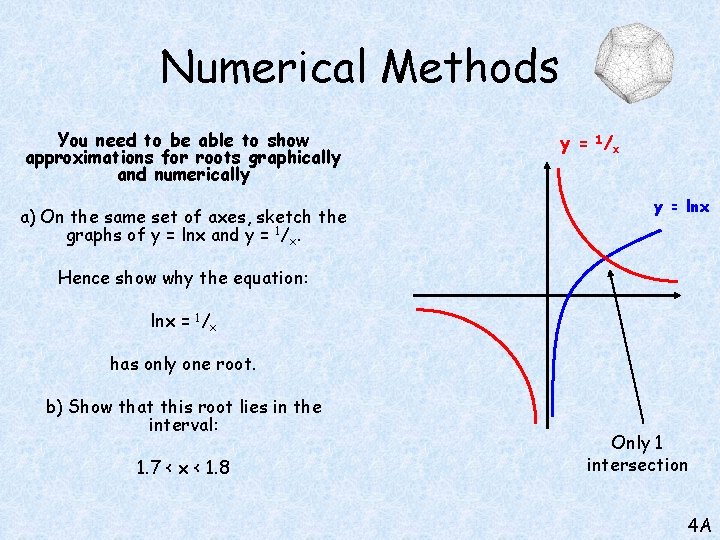
Numerical Methods You need to be able to show approximations for roots graphically and numerically a) On the same set of axes, sketch the graphs of y = lnx and y = 1/x. y = 1/ x y = lnx Hence show why the equation: lnx = 1/x has only one root. b) Show that this root lies in the interval: 1. 7 < x < 1. 8 Only 1 intersection 4 A

Numerical Methods You need to be able to show approximations for roots graphically and numerically a) On the same set of axes, sketch the graphs of y = lnx and y = 1/x. lnx = 1/x lnx - 1/x = 0 Subtract 1/x Hence show why the equation: lnx = 1/x ln(1. 7) - 1/1. 7 has only one root. = -0. 0576 b) Show that this root lies in the interval: 1. 7 < x < 1. 8 ln(1. 8) - 1/1. 8 = 0. 0322 The sign has changed from negative to positive, so the root must be in this interval! 4 A

Numerical Methods You are able to work out lots of different types of sum: For example, Multiplying. You could use the grid method …But how would you work out square roots? Addition or Subtraction. You use the column method You could use a calculator, but what is the calculator doing? You can divide using the bus shelter You can also deal with powers and fractions 4 B

Numerical Methods Calculating Square Roots This formula will calculate a square root Your calculator will use a method called ‘iteration’ xn is the first guess This involves putting a ‘guess’ number into a formula, and getting an answer The answer is then put back into the formula, to get another answer This process is repeated many times, and each time, the answer becomes more accurate xn + 1 is the answer which will be put in again a is the number being rooted So if we want to calculate √ 3… 4 B

Numerical Methods Calculating Square Roots Your calculator will use a method called ‘iteration’ This involves putting a ‘guess’ number into a formula, and getting an answer The answer is then put back into the formula, to get another answer This process is reapeated many times, and each time, the answer becomes more accurate Using iteration to find √ 3 a = 3, we can use 2 as our ‘first guess’ (x 0) Type into the calculator (this would once have been done by hand!) a = 3, we now use 1. 75 (x 1) Type into the calculator (this would once have been done by hand!) 4 B

Numerical Methods Calculating Square Roots Your calculator will use a method called ‘iteration’ This involves putting a ‘guess’ number into a formula, and getting an answer The answer is then put back into the formula, to get another answer This process is reapeated many times, and each time, the answer becomes more accurate Using iteration to find √ 3 a = 3, use the previous answer again Make use of the Ans button on your calculator. After this you can effectively just keep pressing the = sign! Keep going like this and you get closer to the exact answer to √ 3! 4 B

Numerical Methods You can use iteration to find approximations for f(x) = 0, to any desired degree of accuracy… a) Show that: Add 4 x, Subtract 1 Divide by x can be written in the form: 4 B

Numerical Methods You can use iteration to find approximations for f(x) = 0, to any desired degree of accuracy… b) Use the iteration formula: to find, to 2 decimal places, a root of the equation: Use x 0 = 3 You do not need to write this out every single time, but a few examples are needed After a few iterations, the first few decimal places stop changing 3. 73 to 2 dp 4 B

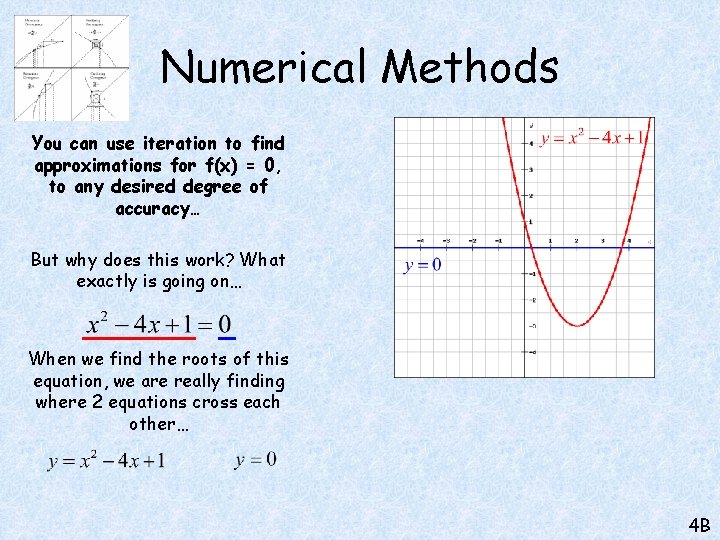
Numerical Methods You can use iteration to find approximations for f(x) = 0, to any desired degree of accuracy… But why does this work? What exactly is going on… When we find the roots of this equation, we are really finding where 2 equations cross each other… 4 B

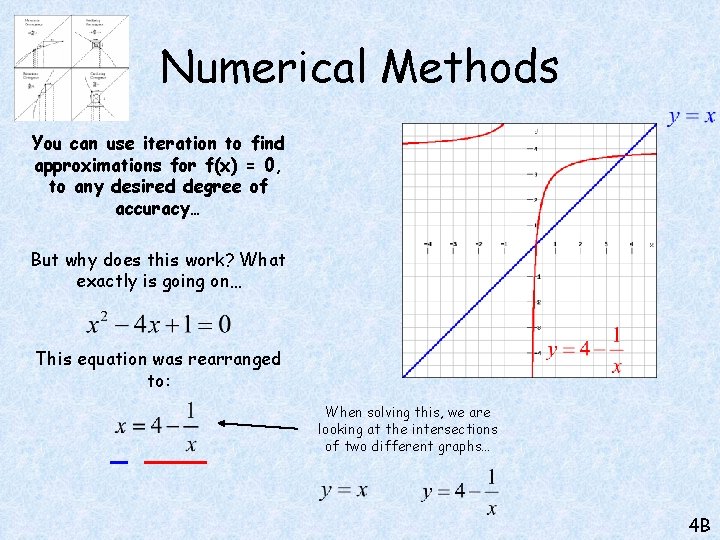
Numerical Methods You can use iteration to find approximations for f(x) = 0, to any desired degree of accuracy… But why does this work? What exactly is going on… This equation was rearranged to: When solving this, we are looking at the intersections of two different graphs… 4 B

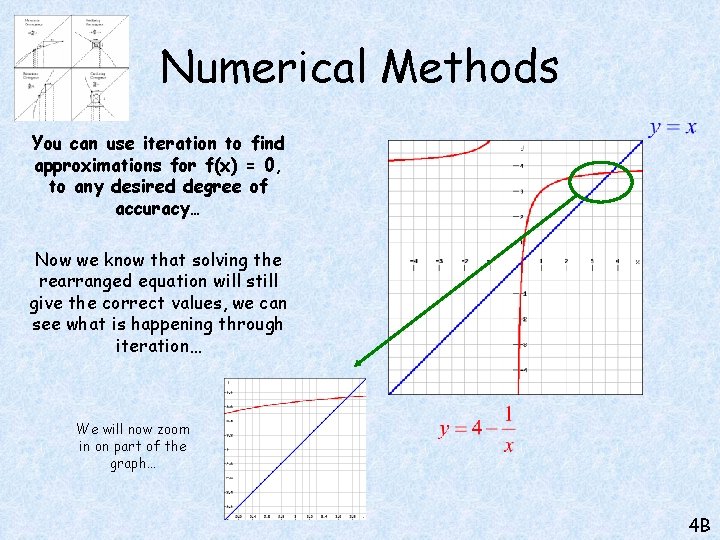
Numerical Methods You can use iteration to find approximations for f(x) = 0, to any desired degree of accuracy… Look at the x values that solve each pair of equations… The point to understand from this is that solving a rearranged equation is the same as solving the original one! 4 B

Numerical Methods You can use iteration to find approximations for f(x) = 0, to any desired degree of accuracy… Now we know that solving the rearranged equation will still give the correct values, we can see what is happening through iteration… We will now zoom in on part of the graph… 4 B

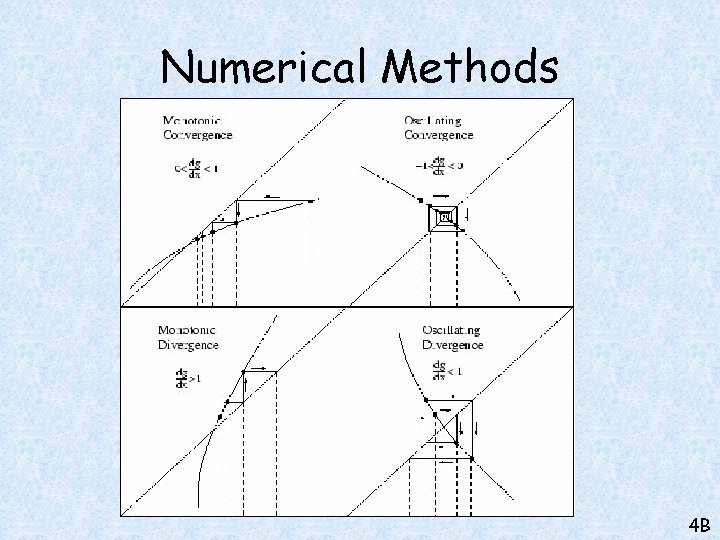
Numerical Methods You can use iteration to find approximations for f(x) = 0, to any desired degree of accuracy… It is important to realise that different starting numbers can result in convergence to different roots Different rearrangements for iteration can also yield different results It is also possible that this will not work and the answers diverge away from any roots. In this case, the correction is to change the starting number ! We assumed x = 3 (Left side) on our first guess This gave us a value of 3. 66 on the right side We then took this for our new x-value (Left side) Putting into the right side gave us a new value of 3. 72 The process causes the xvalues to converge at a root… 4 B

Numerical Methods 4 B

Numerical Methods You can use iteration to find approximations for f(x) = 0, to any desired degree of accuracy… Add 5 x, Add 3 Square root Show that: Can be written either as: Add 5 x or Divide by 5 4 B

Numerical Methods You can use iteration to find approximations for f(x) = 0, to any desired degree of accuracy… Show that the iteration formulae: Give different roots of the equation: Use x 0 = 5 x 4 is usually enough unless specified! 4 B

Numerical Methods You can use iteration to find approximations for f(x) = 0, to any desired degree of accuracy… Show that the iteration formulae: Give different roots of the equation: Use x 0 = 5 Sometimes you will have to go further in order to find answers to a given number of decimal places… 4 B

Summary • We have looked at various numerical methods that can be used to approximate solutions to equations • We have seen how to rearrange formulae for iteration • We have seen how iteration works…