Introduction This Chapter focuses on sketching Graphs We

Introduction • This Chapter focuses on sketching Graphs • We will also be looking at using them to solve Equations • There will also be some work on Graph transformations

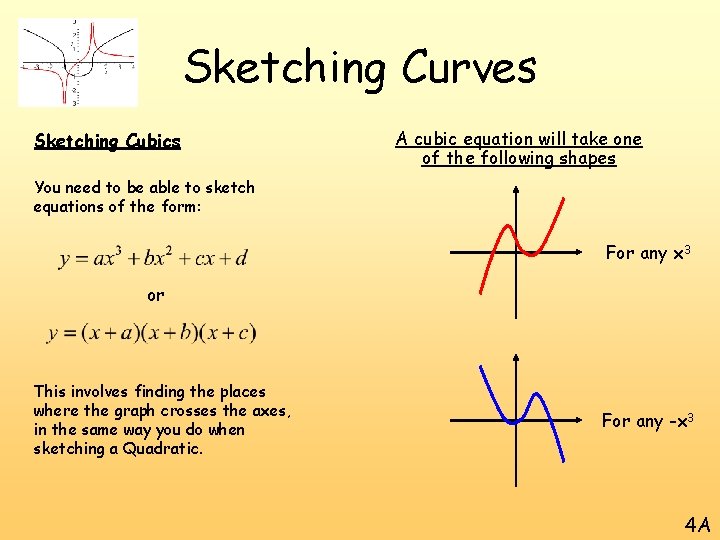
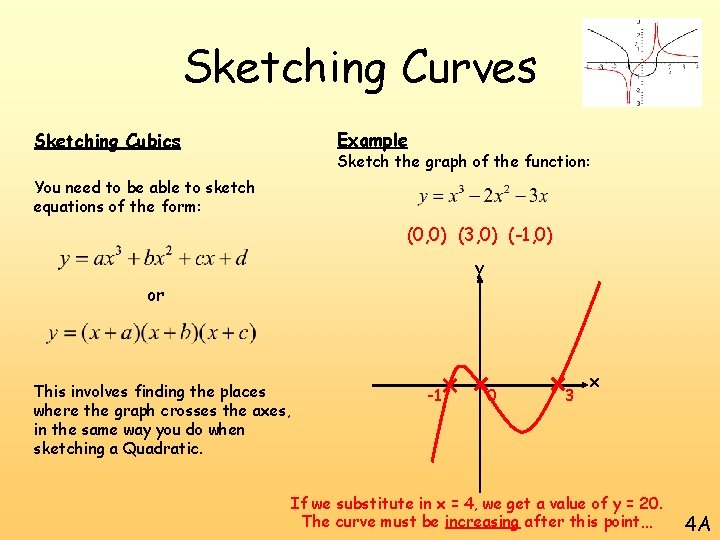
Sketching Curves Sketching Cubics A cubic equation will take one of the following shapes You need to be able to sketch equations of the form: For any x 3 or This involves finding the places where the graph crosses the axes, in the same way you do when sketching a Quadratic. For any -x 3 4 A

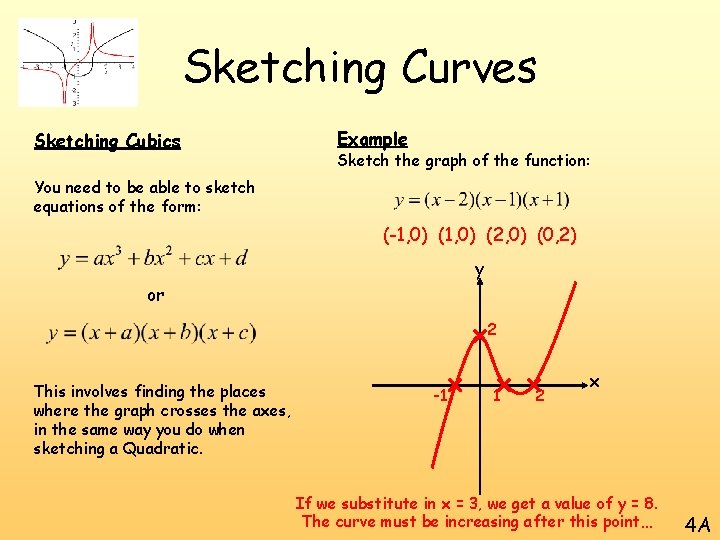
Sketching Curves Sketching Cubics Example Sketch the graph of the function: You need to be able to sketch equations of the form: If y = 0 or So x = 2, 1 or -1 (-1, 0) (1, 0) and (2, 0) This involves finding the places where the graph crosses the axes, in the same way you do when sketching a Quadratic. If x = 0 So y = 2 (0, 2) 4 A

Sketching Curves Sketching Cubics Example Sketch the graph of the function: You need to be able to sketch equations of the form: (-1, 0) (2, 0) (0, 2) y or 2 This involves finding the places where the graph crosses the axes, in the same way you do when sketching a Quadratic. -1 1 2 x If we substitute in x = 3, we get a value of y = 8. The curve must be increasing after this point… 4 A

Sketching Curves Sketching Cubics Example Sketch the graph of the function: You need to be able to sketch equations of the form: If y = 0 or So x = 2, 1 or -1 (-1, 0) (1, 0) and (2, 0) This involves finding the places where the graph crosses the axes, in the same way you do when sketching a Quadratic. If x = 0 So y = -2 (0, -2) 4 A

Sketching Curves Sketching Cubics Example Sketch the graph of the function: You need to be able to sketch equations of the form: (-1, 0) (2, 0) (0, -2) y or This involves finding the places where the graph crosses the axes, in the same way you do when sketching a Quadratic. -1 1 2 x -2 If we substitute in x = 3, we get a value of y = -8. The curve must be decreasing after this point… 4 A

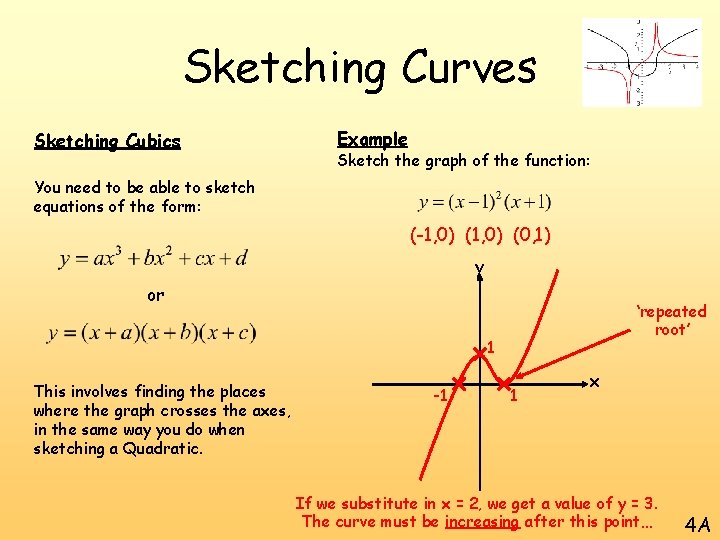
Sketching Curves Sketching Cubics Example Sketch the graph of the function: You need to be able to sketch equations of the form: If y = 0 or So x = 1 or -1 (-1, 0) and (1, 0) This involves finding the places where the graph crosses the axes, in the same way you do when sketching a Quadratic. If x = 0 So y = 1 (0, 1) 4 A

Sketching Curves Sketching Cubics Example Sketch the graph of the function: You need to be able to sketch equations of the form: (-1, 0) (0, 1) y or ‘repeated root’ 1 This involves finding the places where the graph crosses the axes, in the same way you do when sketching a Quadratic. -1 1 x If we substitute in x = 2, we get a value of y = 3. The curve must be increasing after this point… 4 A

Sketching Curves Sketching Cubics Example Sketch the graph of the function: You need to be able to sketch equations of the form: Factorise fully or If y = 0 So x = 0, 3 or -1 This involves finding the places where the graph crosses the axes, in the same way you do when sketching a Quadratic. (0, 0) (3, 0) and (-1, 0) If x = 0 So y = 0 (0, 0) 4 A

Sketching Curves Example Sketching Cubics Sketch the graph of the function: You need to be able to sketch equations of the form: (0, 0) (3, 0) (-1, 0) y or This involves finding the places where the graph crosses the axes, in the same way you do when sketching a Quadratic. -1 0 3 x If we substitute in x = 4, we get a value of y = 20. The curve must be increasing after this point… 4 A

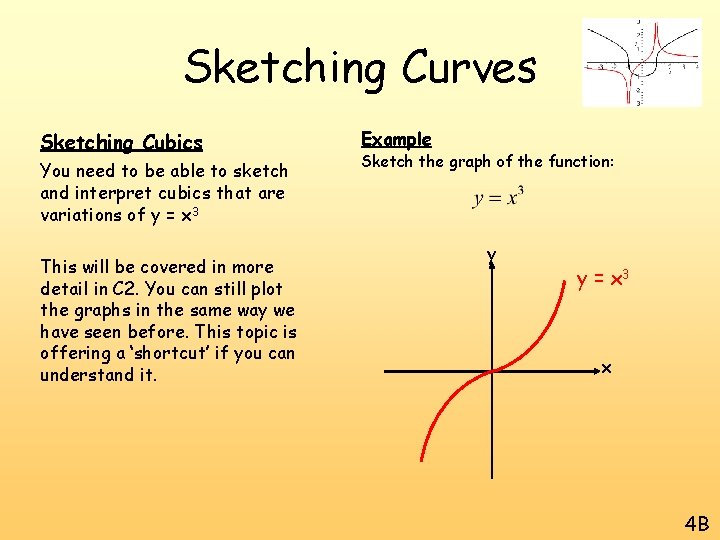
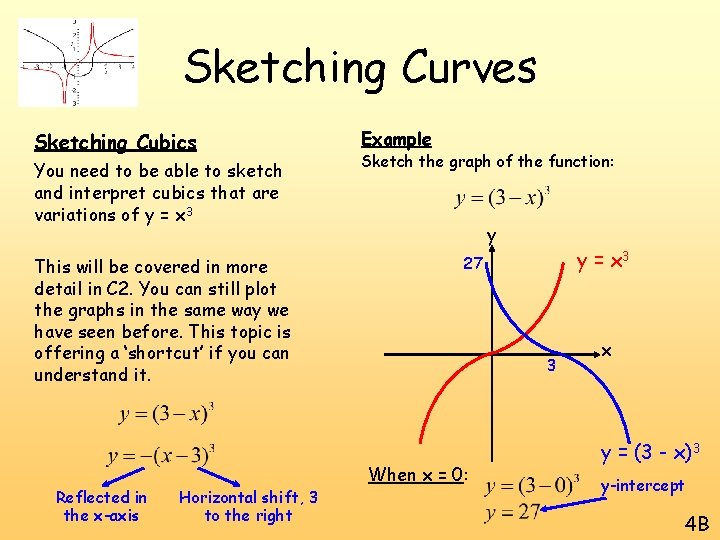
Sketching Curves Sketching Cubics You need to be able to sketch and interpret cubics that are variations of y = x 3 This will be covered in more detail in C 2. You can still plot the graphs in the same way we have seen before. This topic is offering a ‘shortcut’ if you can understand it. Example Sketch the graph of the function: y y = x 3 x 4 B

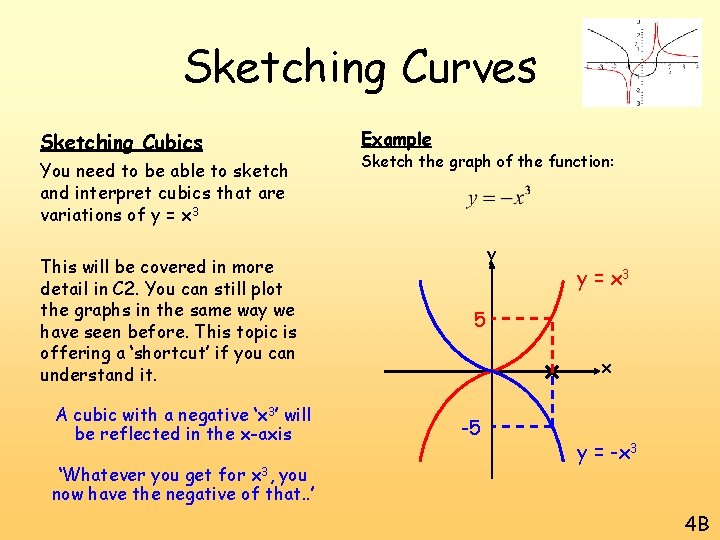
Sketching Curves Sketching Cubics You need to be able to sketch and interpret cubics that are variations of y = x 3 This will be covered in more detail in C 2. You can still plot the graphs in the same way we have seen before. This topic is offering a ‘shortcut’ if you can understand it. A cubic with a negative ‘x 3’ will be reflected in the x-axis ‘Whatever you get for x 3, you now have the negative of that. . ’ Example Sketch the graph of the function: y y = x 3 5 x -5 y = -x 3 4 B

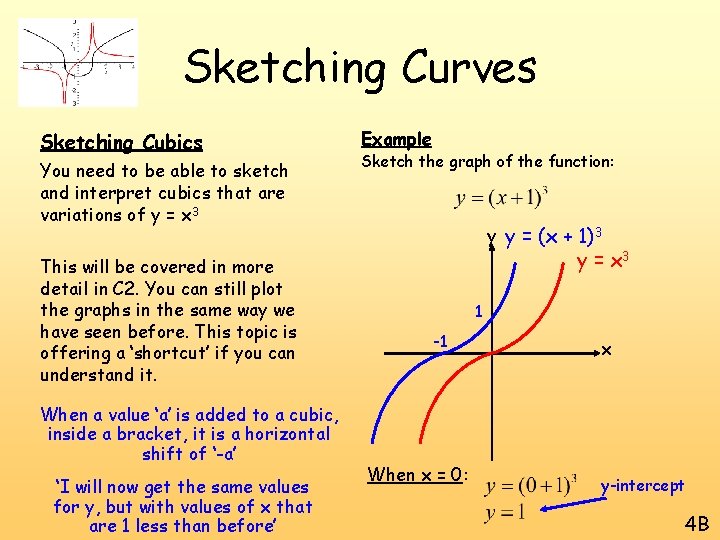
Sketching Curves Sketching Cubics You need to be able to sketch and interpret cubics that are variations of y = x 3 This will be covered in more detail in C 2. You can still plot the graphs in the same way we have seen before. This topic is offering a ‘shortcut’ if you can understand it. When a value ‘a’ is added to a cubic, inside a bracket, it is a horizontal shift of ‘-a’ ‘I will now get the same values for y, but with values of x that are 1 less than before’ Example Sketch the graph of the function: y y = (x + 1)3 y = x 3 1 -1 When x = 0: x y-intercept 4 B

Sketching Curves Sketching Cubics You need to be able to sketch and interpret cubics that are variations of y = x 3 This will be covered in more detail in C 2. You can still plot the graphs in the same way we have seen before. This topic is offering a ‘shortcut’ if you can understand it. Reflected in the x-axis Horizontal shift, 3 to the right Example Sketch the graph of the function: y y = x 3 27 3 When x = 0: x y = (3 - x)3 y-intercept 4 B

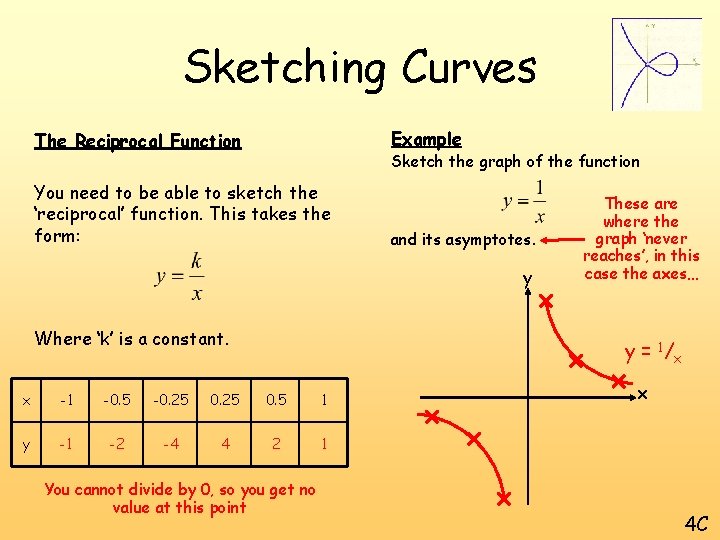
Sketching Curves Example The Reciprocal Function Sketch the graph of the function You need to be able to sketch the ‘reciprocal’ function. This takes the form: and its asymptotes. y Where ‘k’ is a constant. These are where the graph ‘never reaches’, in this case the axes… y = 1 /x x -1 -0. 5 -0. 25 0. 5 1 y -1 -2 -4 4 2 1 You cannot divide by 0, so you get no value at this point x 4 C

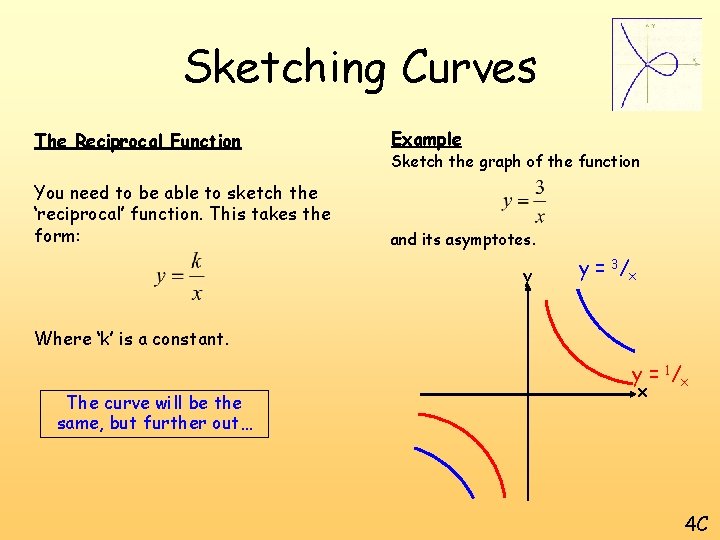
Sketching Curves The Reciprocal Function Example You need to be able to sketch the ‘reciprocal’ function. This takes the form: and its asymptotes. Sketch the graph of the function y y = 3/x Where ‘k’ is a constant. The curve will be the same, but further out… y = 1 /x x 4 C

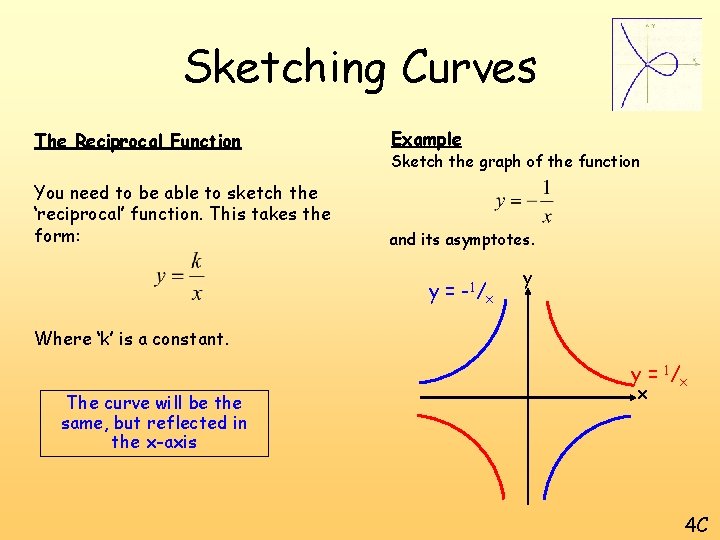
Sketching Curves The Reciprocal Function Example You need to be able to sketch the ‘reciprocal’ function. This takes the form: and its asymptotes. Sketch the graph of the function y= -1/ x y Where ‘k’ is a constant. The curve will be the same, but reflected in the x-axis y = 1 /x x 4 C

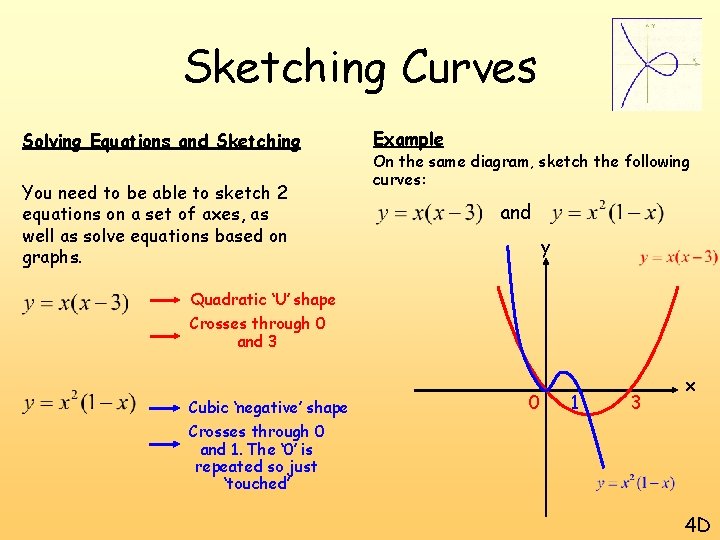
Sketching Curves Solving Equations and Sketching You need to be able to sketch 2 equations on a set of axes, as well as solve equations based on graphs. Example On the same diagram, sketch the following curves: and y Quadratic ‘U’ shape Crosses through 0 and 3 Cubic ‘negative’ shape Crosses through 0 and 1. The ‘ 0’ is repeated so just ‘touched’ 0 1 3 x 4 D

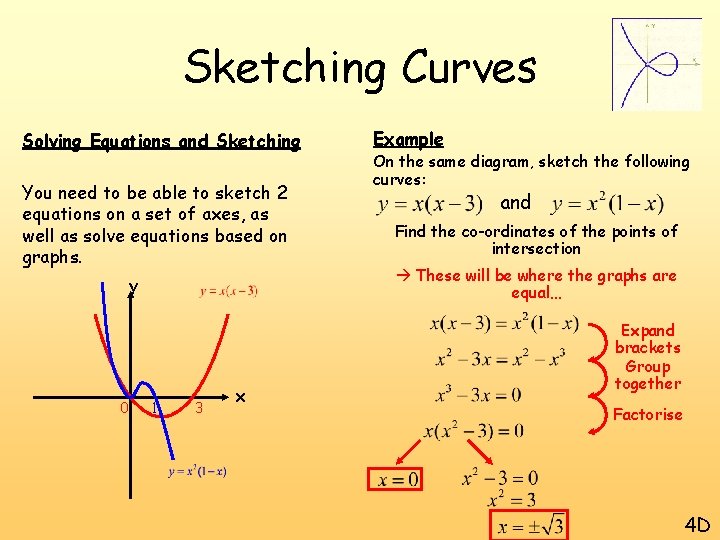
Sketching Curves Solving Equations and Sketching You need to be able to sketch 2 equations on a set of axes, as well as solve equations based on graphs. y 0 1 3 x Example On the same diagram, sketch the following curves: and Find the co-ordinates of the points of intersection These will be where the graphs are equal… Expand brackets Group together Factorise 4 D

Sketching Curves Solving Equations and Sketching You need to be able to sketch 2 equations on a set of axes, as well as solve equations based on graphs. x=-√ 3 x=0 x=√ 3 Example On the same diagram, sketch the following curves: and Find the co-ordinates of the points of intersection These will be where the graphs are equal… Expand brackets Group together Factorise (-√ 3 , 3+3√ 3) (0, 0) (√ 3 , 3 -3√ 3) 4 D

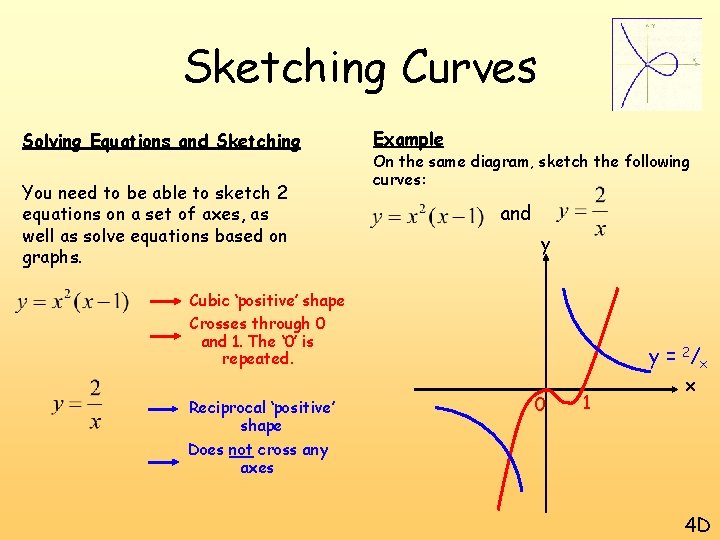
Sketching Curves Solving Equations and Sketching You need to be able to sketch 2 equations on a set of axes, as well as solve equations based on graphs. Example On the same diagram, sketch the following curves: and y Cubic ‘positive’ shape Crosses through 0 and 1. The ‘ 0’ is repeated. Reciprocal ‘positive’ shape y = 2/x 0 1 x Does not cross any axes 4 D

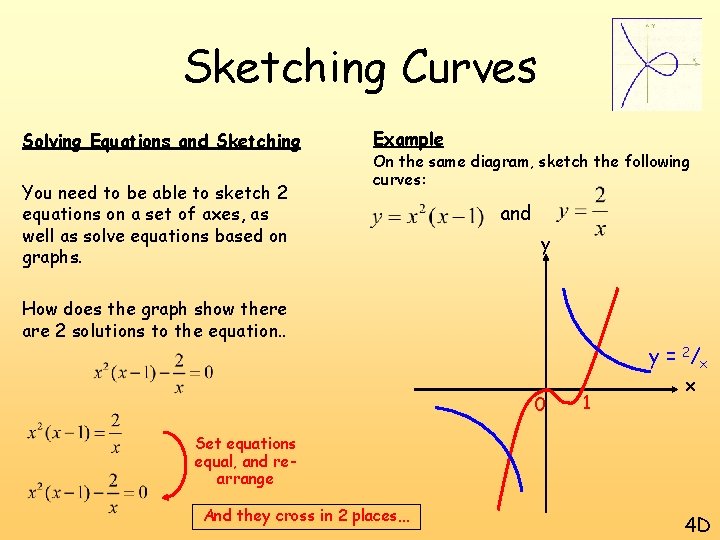
Sketching Curves Solving Equations and Sketching You need to be able to sketch 2 equations on a set of axes, as well as solve equations based on graphs. Example On the same diagram, sketch the following curves: and y How does the graph show there are 2 solutions to the equation. . y = 2/x 0 1 x Set equations equal, and rearrange And they cross in 2 places… 4 D

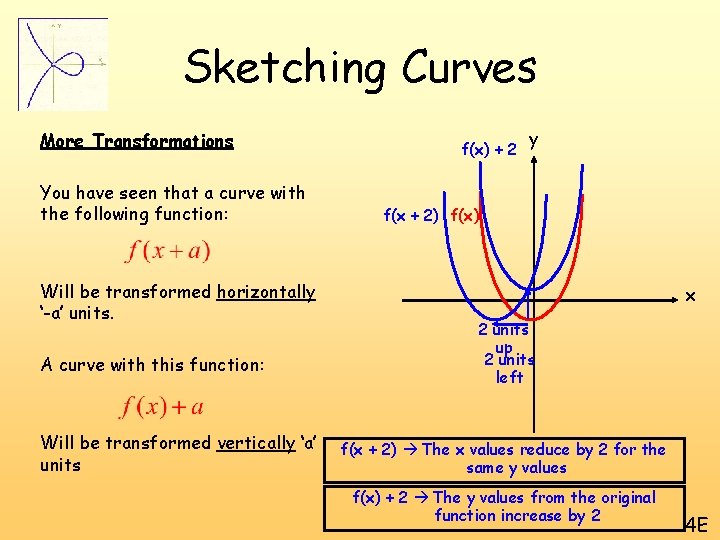
Sketching Curves More Transformations You have seen that a curve with the following function: Will be transformed horizontally ‘-a’ units. A curve with this function: Will be transformed vertically ‘a’ units f(x) + 2 y f(x + 2) f(x) x 2 units up 2 units left f(x + 2) The x values reduce by 2 for the same y values f(x) + 2 The y values from the original function increase by 2 4 E

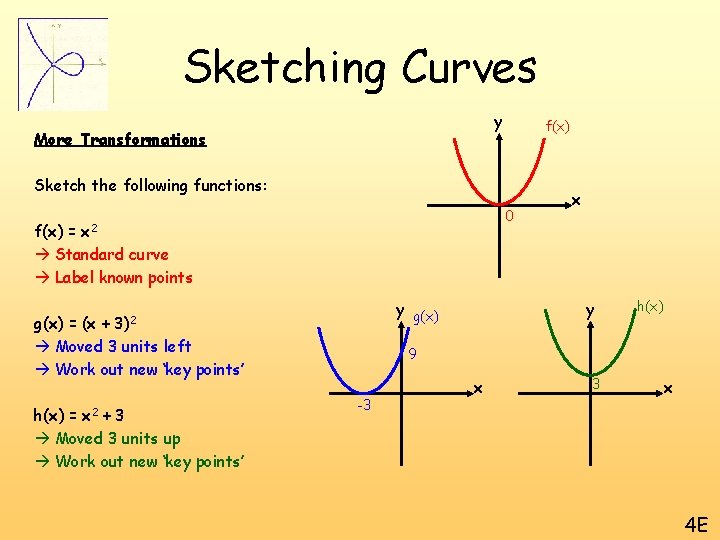
Sketching Curves y More Transformations f(x) Sketch the following functions: 0 x 2 f(x) = Standard curve Label known points h(x) = x 2 + 3 Moved 3 units up Work out new ‘key points’ y y g(x) = (x + 3)2 Moved 3 units left Work out new ‘key points’ x h(x) 9 -3 x 4 E

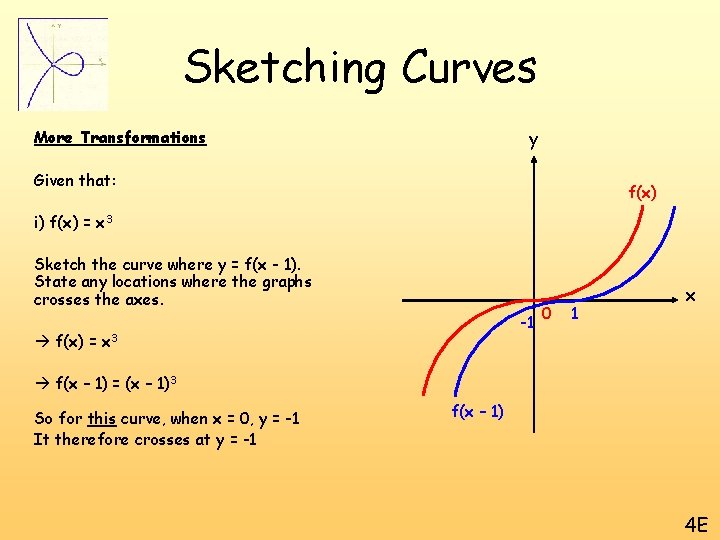
Sketching Curves y More Transformations Given that: f(x) i) f(x) = x 3 Sketch the curve where y = f(x - 1). State any locations where the graphs crosses the axes. -1 f(x) = x 3 0 1 x f(x – 1) = (x – 1)3 So for this curve, when x = 0, y = -1 It therefore crosses at y = -1 f(x – 1) 4 E

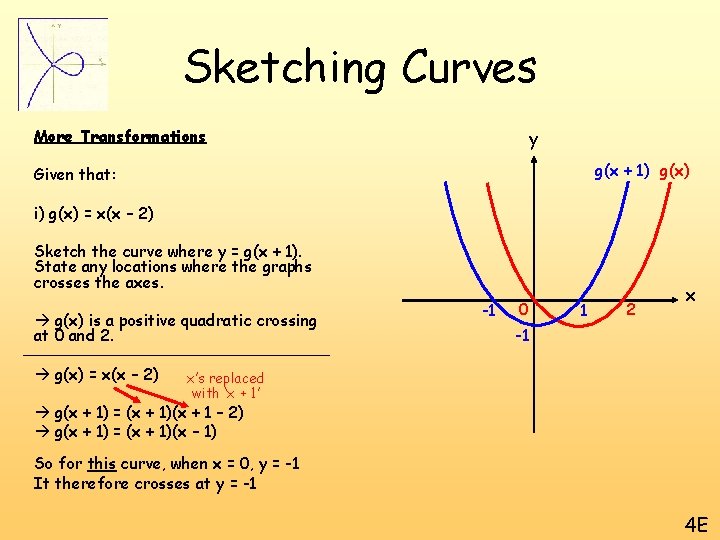
Sketching Curves More Transformations y g(x + 1) g(x) Given that: i) g(x) = x(x – 2) Sketch the curve where y = g(x + 1). State any locations where the graphs crosses the axes. g(x) is a positive quadratic crossing at 0 and 2. g(x) = x(x – 2) -1 0 1 2 x -1 x’s replaced with ‘x + 1’ g(x + 1) = (x + 1)(x + 1 – 2) g(x + 1) = (x + 1)(x – 1) So for this curve, when x = 0, y = -1 It therefore crosses at y = -1 4 E

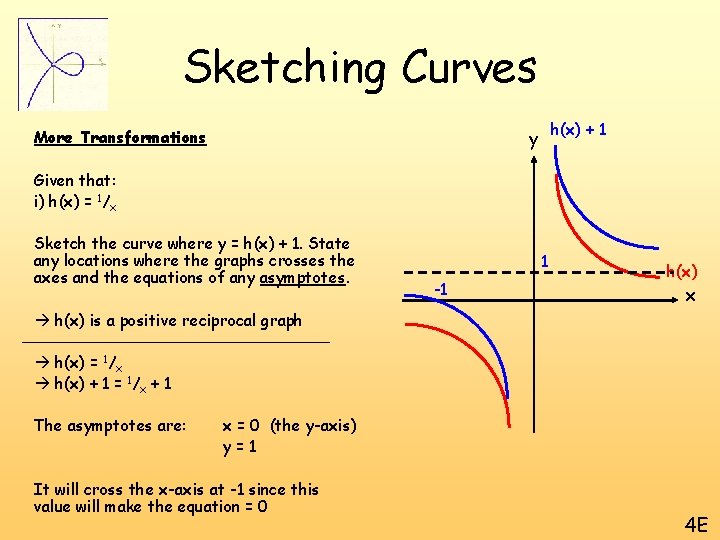
Sketching Curves h(x) + 1 y More Transformations Given that: i) h(x) = 1/x Sketch the curve where y = h(x) + 1. State any locations where the graphs crosses the axes and the equations of any asymptotes. 1 -1 h(x) x h(x) is a positive reciprocal graph h(x) = 1/x h(x) + 1 = 1/x + 1 The asymptotes are: x = 0 (the y-axis) y=1 It will cross the x-axis at -1 since this value will make the equation = 0 4 E

Sketching Curves Even more Transformations You also need to be able to perform transformations of the form: this is a horizontal stretch of 1/a. ‘We will get the same y values, using half the x values’ This is because the x values get multiplied by 2 before the y values are worked out You also need to know: this is a vertical stretch by factor ‘a’ ‘We will get y values twice as big, using the same x values’ This is because when we work out the y values, they are doubled after 4 F

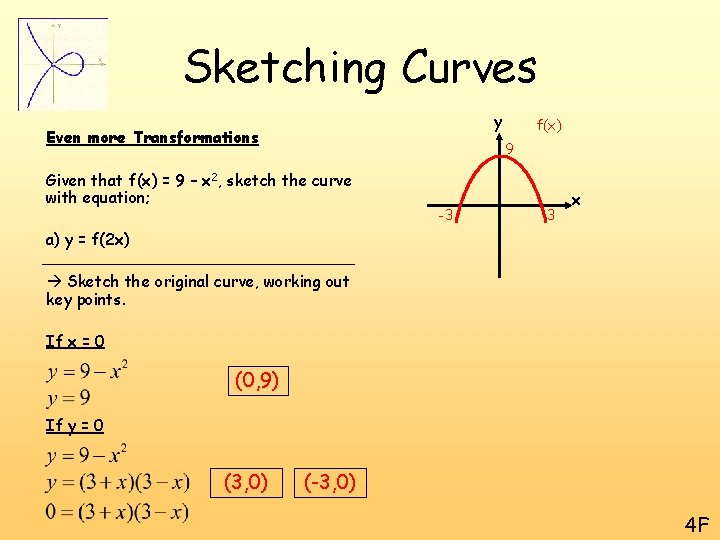
Sketching Curves y Even more Transformations f(x) 9 Given that f(x) = 9 – x 2, sketch the curve with equation; -3 3 x a) y = f(2 x) Sketch the original curve, working out key points. If x = 0 (0, 9) If y = 0 (3, 0) (-3, 0) 4 F

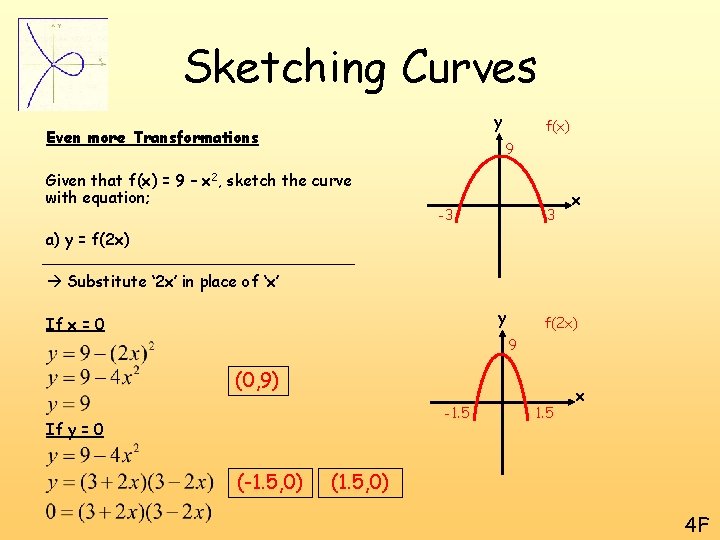
Sketching Curves y Even more Transformations f(x) 9 Given that f(x) = 9 – x 2, sketch the curve with equation; -3 3 x a) y = f(2 x) Substitute ‘ 2 x’ in place of ‘x’ y If x = 0 f(2 x) 9 (0, 9) -1. 5 If y = 0 (-1. 5, 0) 1. 5 x (1. 5, 0) 4 F

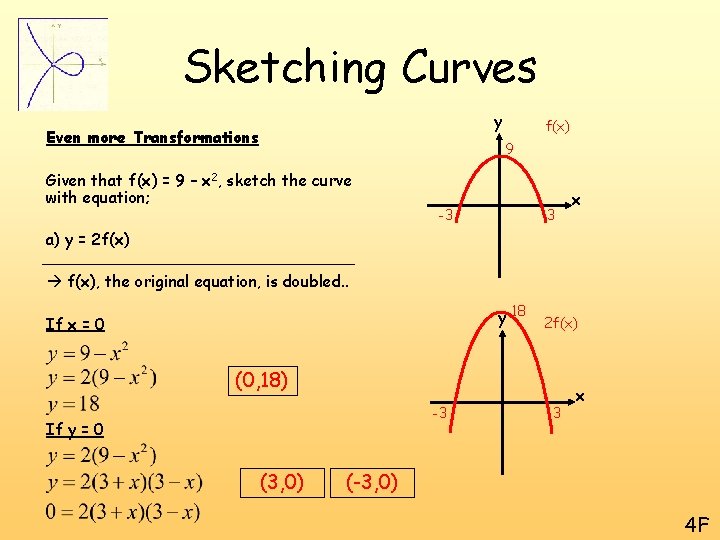
Sketching Curves y Even more Transformations f(x) 9 Given that f(x) = 9 – x 2, sketch the curve with equation; -3 3 x a) y = 2 f(x) f(x), the original equation, is doubled. . y 18 If x = 0 2 f(x) (0, 18) -3 If y = 0 (3, 0) 3 x (-3, 0) 4 F

Summary • We have learnt the shapes of several different curves • We have learnt how to apply transformations to those curves • We have also looked at how to work out the ‘key points’