Introduction Students activity Topic of discussion Pythagoras Theorem

Introduction • • • Students’ activity Topic of discussion: Pythagoras’ Theorem Historical background Proof of Pythagoras’ Theorem Typical examples Classwork 1 (worksheets given) Applications of Pythagoras Theorem to long questions Classwork 2 Homework Summary

Students’ Activity

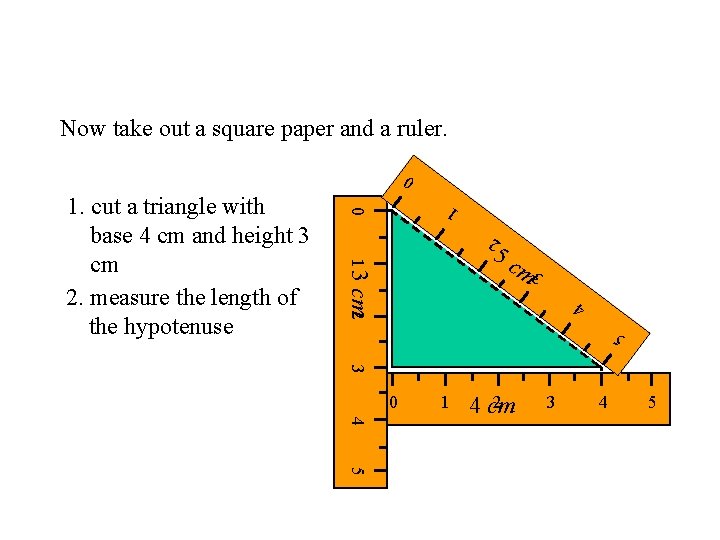
Now take out a square paper and a ruler. 0 0 1 m 2 cm 2 3 5 c 13 4 5 1. cut a triangle with base 4 cm and height 3 cm 2. measure the length of the hypotenuse 3 0 1 4 2 4 cm 3 4 5 5

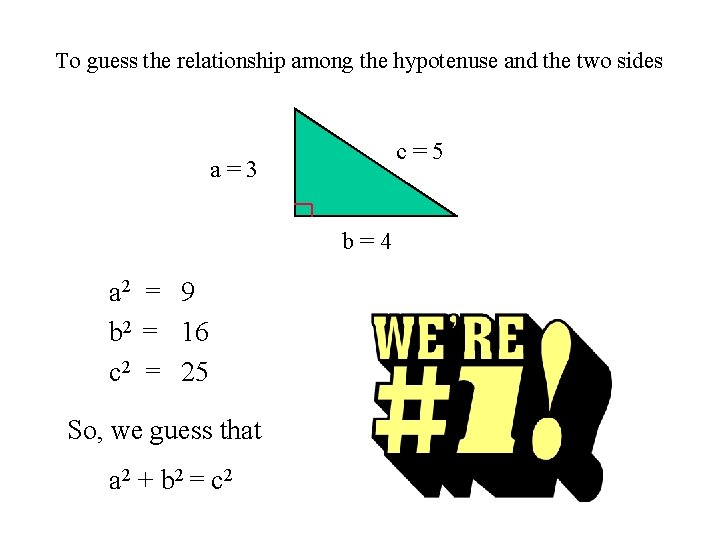
To guess the relationship among the hypotenuse and the two sides c=5 a=3 b=4 a 2 = 9 b 2 = 16 c 2 = 25 So, we guess that a 2 + b 2 = c 2

Topics of discussion: Pythagoras’ Theorem

Pythagoras’ Theorem a c b Hypotenuse - it is the side opposite to the right angle For any right-angled triangle, c is the length of the hypotenuse, a and b are the length of the other 2 sides, then c 2 = a 2+ b 2

Historical Background

Pythagoras’ Theorem 畢氏定理 Pythagoras 畢達哥拉斯(~580 -500 B. C. ) He was a Greek philosopher responsible for important developments in mathematics, astronomy and theory of music.

Proof of Pythagoras’ Theorem

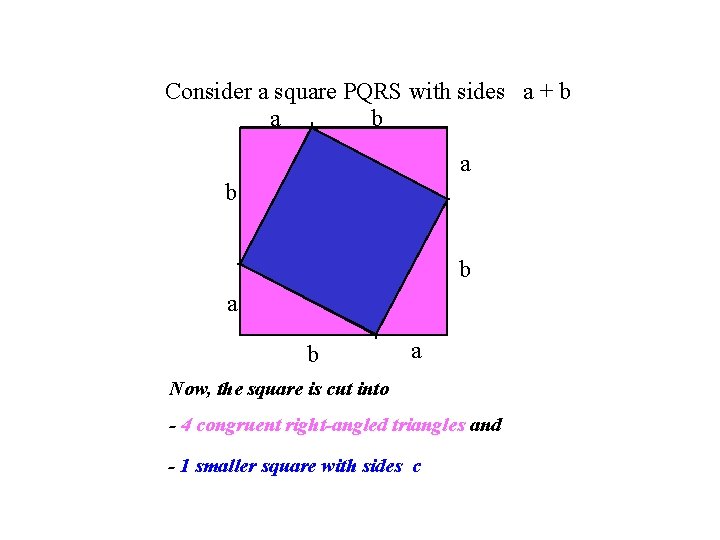
Consider a square PQRS with sides a + b a b b a a c c c b a Now, the square is cut into - 4 congruent right-angled triangles and - 1 smaller square with sides c

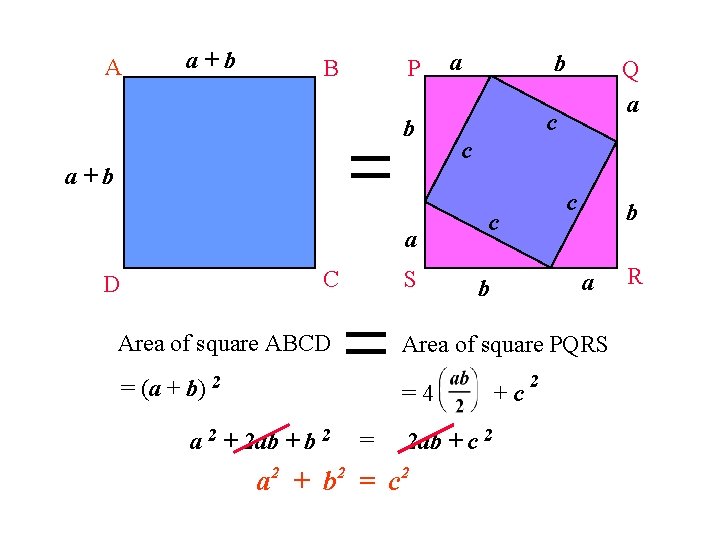
A a+b B P b a b c c a+b a S C D Area of square ABCD c c b a b Area of square PQRS = (a + b) 2 =4 a 2 + 2 ab + b 2 Q a = 2 ab + c 2 a 2 + b 2 = c 2 +c 2 R

Typical Examples

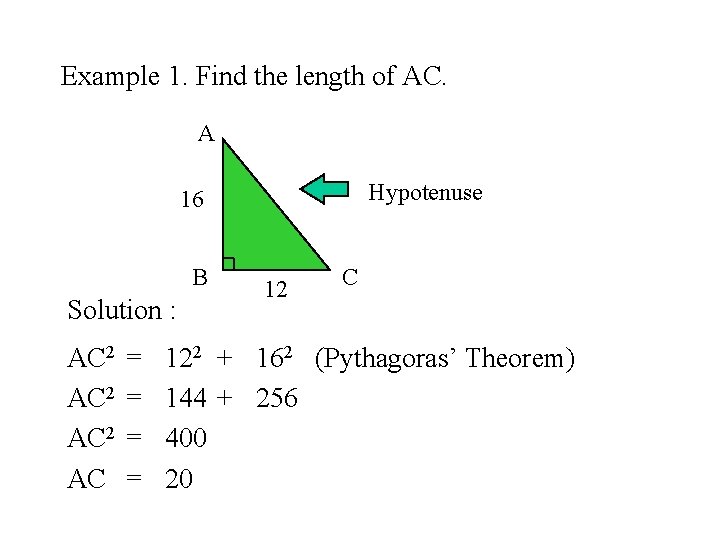
Example 1. Find the length of AC. A Hypotenuse 16 B Solution : AC 2 AC = = 12 C 122 + 162 (Pythagoras’ Theorem) 144 + 256 400 20

Example 2. Find the length of QR. R Solution : 252 = QR = P 24 25 Hypotenuse Q 242 + QR 2 625 - 576 49 7 (Pythagoras’ Theorem)

Classwork 1 (Worksheets Given)

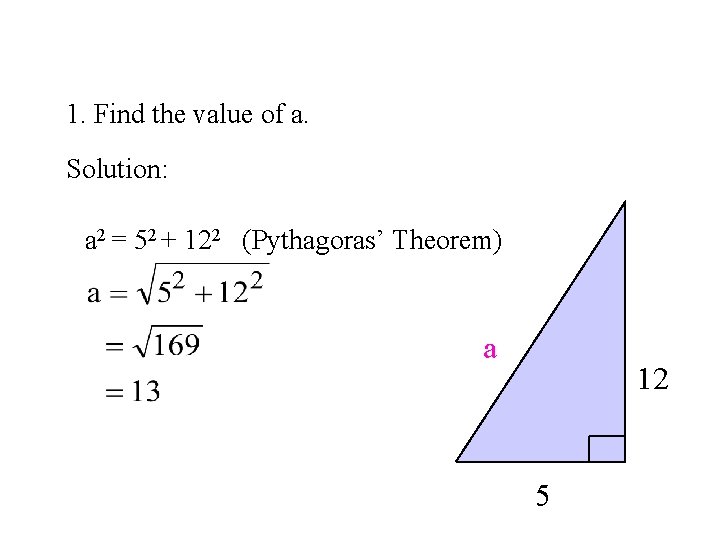
1. Find the value of a. Solution: a 2 = 52 + 122 (Pythagoras’ Theorem) a 12 5

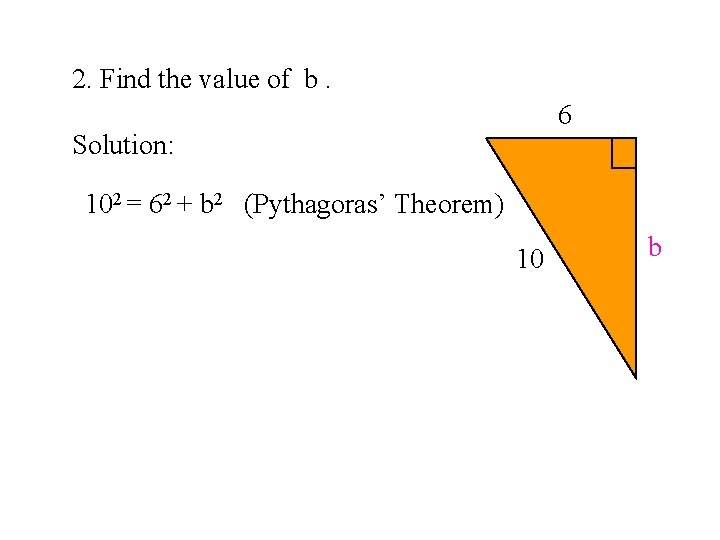
2. Find the value of b. 6 Solution: 102 = 62 + b 2 (Pythagoras’ Theorem) 10 b

3. Find the value of c. Solution: 252 = 72 + c 2 (Pythagoras’ Theorem) c 7 25

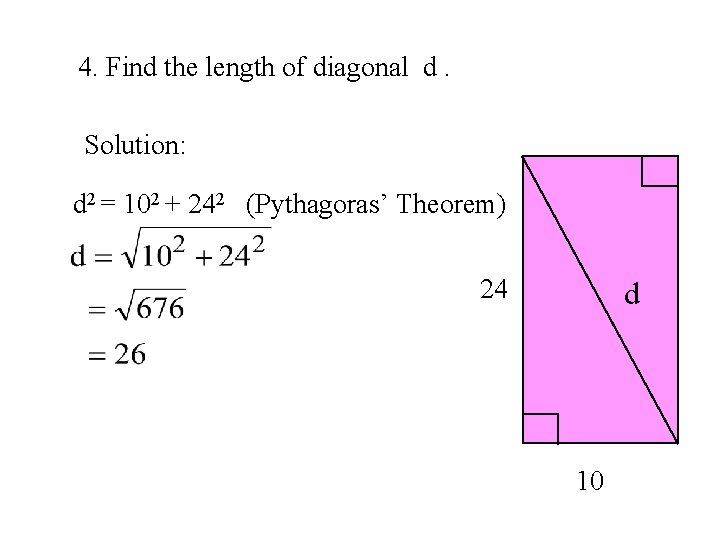
4. Find the length of diagonal d. Solution: d 2 = 102 + 242 (Pythagoras’ Theorem) 24 d 10

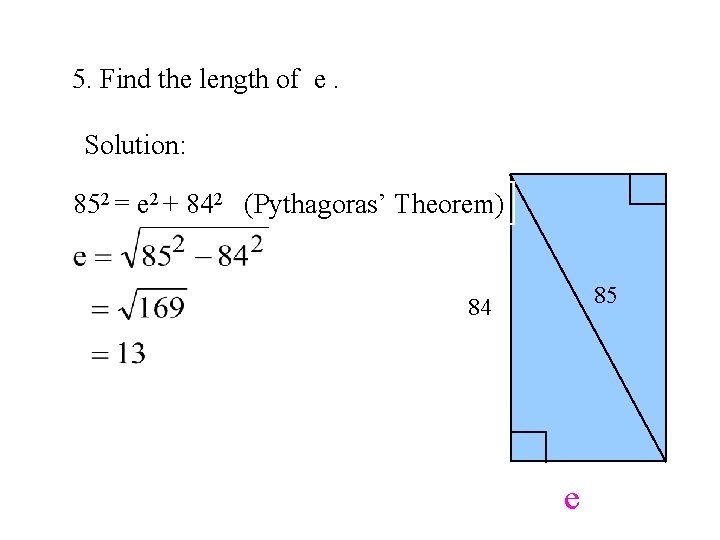
5. Find the length of e. Solution: 852 = e 2 + 842 (Pythagoras’ Theorem) 85 84 e

Applications of Pythagoras’ Theorem to Long Questions

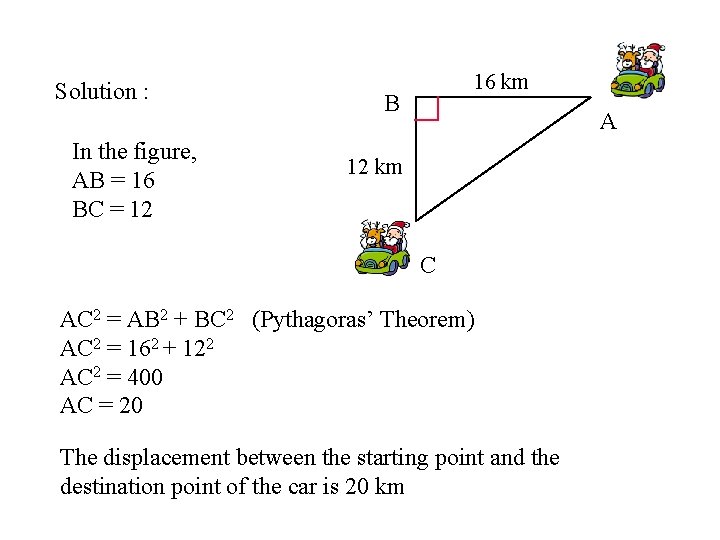
Application of Pythagoras’ Theorem A car travels 16 km from east to west. Then it turns left and travels a further 12 km. Find the displacement between the starting point and the destination point of the car. 16 km N 12 km ?

Solution : In the figure, AB = 16 BC = 12 16 km B A 12 km C AC 2 = AB 2 + BC 2 (Pythagoras’ Theorem) AC 2 = 162 + 122 AC 2 = 400 AC = 20 The displacement between the starting point and the destination point of the car is 20 km

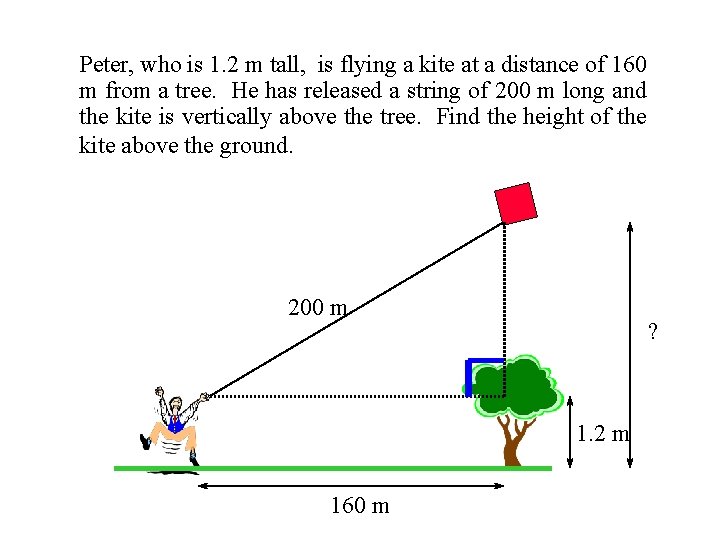
Peter, who is 1. 2 m tall, is flying a kite at a distance of 160 m from a tree. He has released a string of 200 m long and the kite is vertically above the tree. Find the height of the kite above the ground. 200 m ? 1. 2 m 160 m

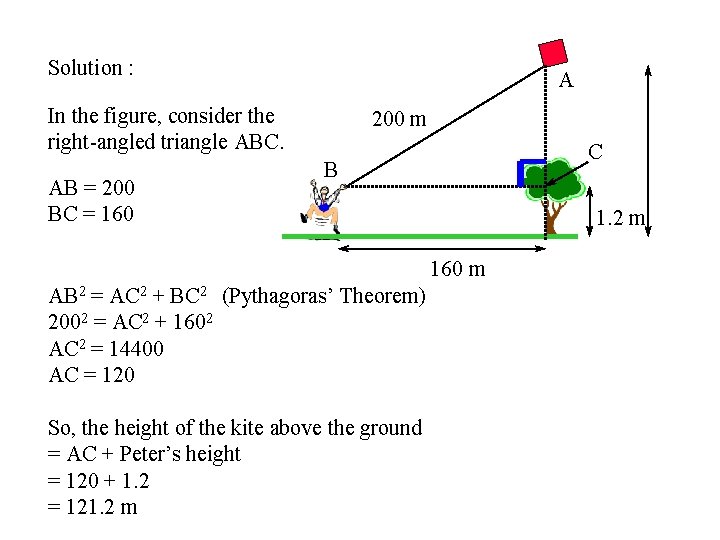
Solution : A In the figure, consider the right-angled triangle ABC. AB = 200 BC = 160 200 m C B 1. 2 m 160 m AB 2 = AC 2 + BC 2 (Pythagoras’ Theorem) 2002 = AC 2 + 1602 AC 2 = 14400 AC = 120 So, the height of the kite above the ground = AC + Peter’s height = 120 + 1. 2 = 121. 2 m

Classwork 2

The height of a tree is 5 m. The distance between the top of it and the tip of its shadow is 13 m. Find the length of the shadow L. Solution: 132 = 52 + L 2 (Pythagoras’ Theorem) L 2 = 132 - 52 L 2 = 144 L = 12 13 m L 5 m

Summary

Summary of Pythagoras’ Theorem For any right-angled triangle, c a b