Introduction Quadratic functions are used to model various

Introduction Quadratic functions are used to model various situations. Some situations are literal, such as determining the shape of a parabola, and some situations involve applying the key features of quadratics to real-life situations. For example, an investor might want to predict the behavior of a particular mutual fund over time, or an NFL scout might want to determine the maximum height of a ball kicked by a potential football punter. In this lesson, we will look specifically at the vertex form of a quadratic, f(x) = a(x – h)2 + k, where the vertex is the point (h, k). The vertex can be read directly from the equation. 5. 3. 3: Creating and Graphing Equations Using Vertex Form 1

Key Concepts • Standard form, intercept form, and vertex form are equivalent expressions written in different forms. • Standard form: f(x) = ax 2 + bx + c, where a is the coefficient of the quadratic term, b is the coefficient of the linear term, and c is the constant term • Intercept form: f(x) = a(x – p)(x – q), where p and q are the zeros of the function • Vertex form: f(x) = a(x – h)2 + k, where the vertex of the parabola is the point (h, k) 2 5. 3. 3: Creating and Graphing Equations Using Vertex Form

Key Concepts, continued • To identify the vertex directly from an equation in vertex form, identify h (the x-coordinate of the vertex) and k (the y-coordinate of the vertex). • Note that the original equation in vertex form has the quantity x – h, so if the equation has a subtraction sign the value of h is h. • This is true because x – (–h) simplifies to x + h. 3 5. 3. 3: Creating and Graphing Equations Using Vertex Form

Key Concepts, continued • However, if the quantity is written as x + h, the value of h is –h. A quadratic function in standard form can be created from vertex form, f(x) = a(x – h)2 + k, where (h, k) is the vertex of the quadratic. • To do so, distribute and simplify by combining like terms. • For example, f(x) = 3(x – 2)2 + 4 becomes f(x) = 3 x 2 – 12 x + 16. 4 5. 3. 3: Creating and Graphing Equations Using Vertex Form

Key Concepts, continued • A quadratic function in vertex form can be created from standard form, f(x) = ax 2 + bx + c. • To do so, complete the square, or determine the value of c that would make ax 2 + bx + c a perfect square trinomial. • To complete the square, take the coefficient of the linear term, divide by the product of 2 and the coefficient of the quadratic term, and square the quotient. 5 5. 3. 3: Creating and Graphing Equations Using Vertex Form

Key Concepts, continued 6 5. 3. 3: Creating and Graphing Equations Using Vertex Form

Key Concepts, continued • Since the quotient of b and 2 a is a constant term, we can combine it with the constant c to get the equation , where • For example, f(x) = 2 x 2 – 12 x + 22 becomes f(x) = 2(x – 3)2 + 4. 7 5. 3. 3: Creating and Graphing Equations Using Vertex Form

Key Concepts, continued • When graphing a quadratic using vertex form, if the vertex is the y-intercept, choose two pairs of symmetric points to plot in order to sketch the most accurate graph. 8 5. 3. 3: Creating and Graphing Equations Using Vertex Form

Common Errors/Misconceptions • forgetting to make sure the coefficient of the quadratic term, x 2, is 1 before completing the square 9 5. 3. 3: Creating and Graphing Equations Using Vertex Form

Guided Practice Example 2 Determine the equation of a quadratic function that has a minimum at (– 4, – 8) and passes through the point (– 2, – 5). 10 5. 3. 3: Creating and Graphing Equations Using Vertex Form

Guided Practice: Example 2, continued 1. Substitute the vertex into f(x) = a(x – h)2 + k Vertex form f(x) = a[x – (– 4)]2 + (– 8) Substitute (– 4, – 8) for h and k. f(x) = a(x + 4)2 – 8 Simplify. 11 5. 3. 3: Creating and Graphing Equations Using Vertex Form

Guided Practice: Example 2, continued 2. Substitute the point (– 2, – 5) into the equation from step 1 and solve for a. f(x) = a(x + 4)2 – 8 Equation – 5 = a[(– 2) + 4]2 – 8 Substitute (– 2, – 5) for x and f(x). – 5 = a(2)2 – 8 Simplify. – 5 = 4 a – 8 3 = 4 a 12 5. 3. 3: Creating and Graphing Equations Using Vertex Form

Guided Practice: Example 2, continued 3. Substitute a into the equation from step 1. f(x) = a(x + 4)2 – 8 The equation of the quadratic function with a minimum at (– 4, – 8) and passing through the point (– 2, – 5) is ✔ 13 5. 3. 3: Creating and Graphing Equations Using Vertex Form

Guided Practice: Example 2, continued 14 5. 3. 3: Creating and Graphing Equations Using Vertex Form

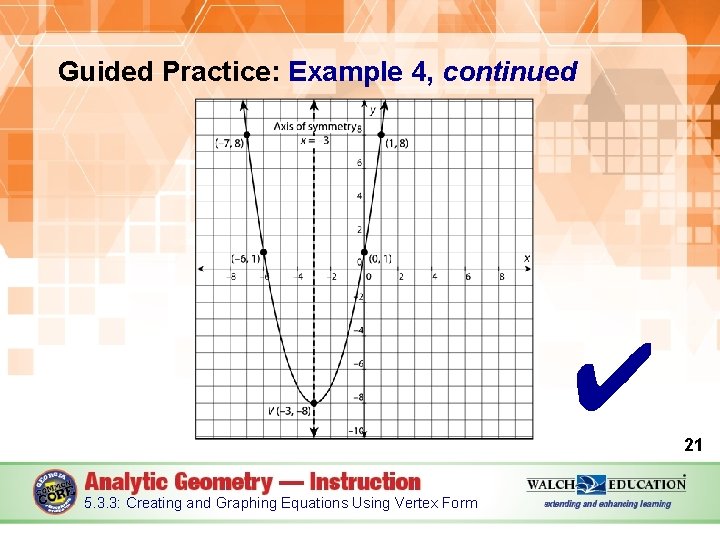
Guided Practice Example 4 Sketch a graph of the quadratic function y = (x + 3)2 – 8. Label the vertex, the axis of symmetry, the y-intercept, and one pair of symmetric points. 15 5. 3. 3: Creating and Graphing Equations Using Vertex Form

Guided Practice: Example 4, continued 1. Identify the vertex and the equation of the axis of symmetry. Given the vertex form of a quadratic function, f(x) = a(x – h)2 + k, the vertex is the point (h, k). The vertex of the quadratic y = (x + 3)2 – 8 is (– 3, – 8). The axis of symmetry extends through the vertex. The equation of the axis of symmetry is x = – 3. 16 5. 3. 3: Creating and Graphing Equations Using Vertex Form

Guided Practice: Example 4, continued 2. Find the y-intercept. The parabola crosses the y-axis when x = 0. Substitute 0 for x to find y. y = (x + 3)2 – 8 Original equation y = (0 + 3)2 – 8 Substitute 0 for x. y = 32 – 8 Simplify. y=1 The y-intercept is the point (0, 1). 5. 3. 3: Creating and Graphing Equations Using Vertex Form 17

Guided Practice: Example 4, continued 3. Find an extra point to the left or right of the axis of symmetry. Choose an x-value and substitute it into the equation to find the corresponding y-value. Typically, choosing x = 1 or x = – 1 is simplest arithmetically, if these numbers aren’t already a part of the vertex or axis of symmetry. In this case, let’s use x = 1. 18 5. 3. 3: Creating and Graphing Equations Using Vertex Form

Guided Practice: Example 4, continued y = (x + 3)2 – 8 Original equation y = (1 + 3)2 – 8 Substitute 1 for x. y = 42 – 8 Simplify. y=8 The parabola passes through the point (1, 8). x = 1 is 4 units to the right of the axis of symmetry, x = – 3. 4 units to the left of the axis of symmetry and horizontal to (1, 8) is the symmetric point (– 7, 8). 5. 3. 3: Creating and Graphing Equations Using Vertex Form 19

Guided Practice: Example 4, continued 4. Plot the points you found in steps 2 and 3 and their symmetric points over the axis of symmetry. 20 5. 3. 3: Creating and Graphing Equations Using Vertex Form

Guided Practice: Example 4, continued ✔ 21 5. 3. 3: Creating and Graphing Equations Using Vertex Form

Guided Practice: Example 4, continued 22 5. 3. 3: Creating and Graphing Equations Using Vertex Form