Introduction Previously we calculated the rate of change

















- Slides: 20

Introduction Previously, we calculated the rate of change of linear functions as well as intervals of exponential functions. We observed that the rate of change of exponential functions changed if we focused on different intervals of the function. Here, we will focus on graphs of linear and exponential functions and learn how to estimate the rates of change. 1 3. 3. 3: Recognizing Average Rate of Change

Key Concepts • To determine the rate of change of a function, first identify the coordinates of the interval being observed. • Sometimes it is necessary to estimate the values for y. • The resulting calculation may be an estimation of the rate of change for the interval identified for the given function. 2 3. 3. 3: Recognizing Average Rate of Change

Key Concepts, continued Estimating Rate of Change from a Graph 1. 2. 3. 4. Determine the interval to be observed. Identify (x 1, y 1) as the starting point of the interval. Identify (x 2, y 2) as the ending point of the interval. Substitute (x 1, y 1) and (x 2, y 2) into the slope formula to calculate the rate of change. 5. The result is the estimated rate of change for the interval between the two points identified. 3 3. 3. 3: Recognizing Average Rate of Change

Common Errors/Misconceptions • incorrectly choosing the values of the indicated interval to estimate the rate of change • incorrectly estimating the values for the indicated interval • substituting incorrect values into the formula for calculating rate of change 4 3. 3. 3: Recognizing Average Rate of Change

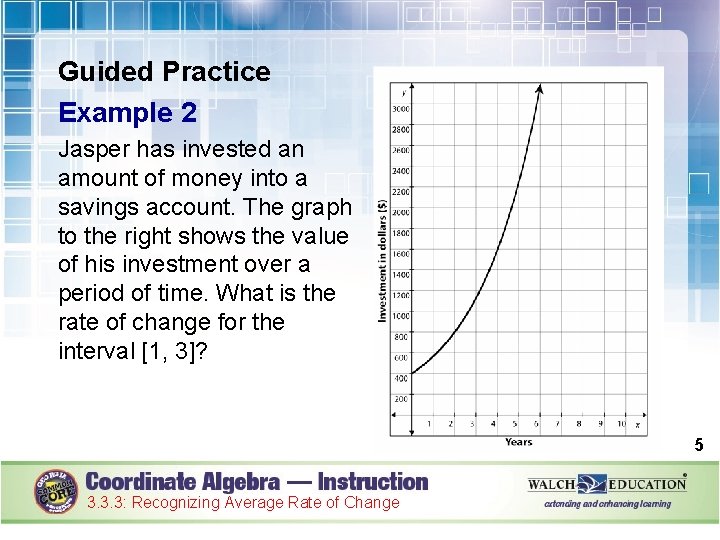
Guided Practice Example 2 Jasper has invested an amount of money into a savings account. The graph to the right shows the value of his investment over a period of time. What is the rate of change for the interval [1, 3]? 5 3. 3. 3: Recognizing Average Rate of Change

Guided Practice: Example 2, continued 1. Determine the interval to be observed. The interval to observe is [1, 3], or where 1 ≤ x ≤ 3. 6 3. 3. 3: Recognizing Average Rate of Change

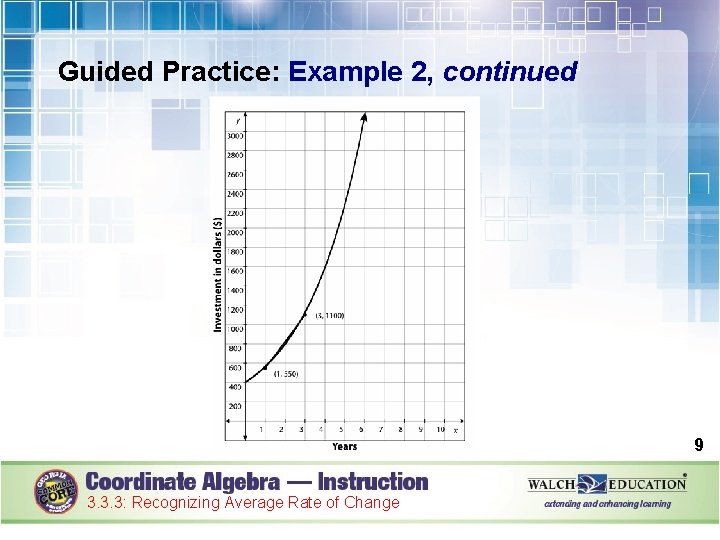
Guided Practice: Example 2, continued 2. Identify the starting point of the interval. The x-value of the starting point is 1. The corresponding y-value is approximately 550. The starting point of the interval is (1, 550). 7 3. 3. 3: Recognizing Average Rate of Change

Guided Practice: Example 2, continued 3. Identify the ending point of the interval. The x-value for the ending point is 3. The corresponding y-value is approximately 1, 100. The ending point of the interval is (3, 1100). 8 3. 3. 3: Recognizing Average Rate of Change

Guided Practice: Example 2, continued 9 3. 3. 3: Recognizing Average Rate of Change

Guided Practice: Example 2, continued 4. Substitute (1, 550) and (3, 1100) into the slope formula to calculate the rate of change. Slope formula Substitute (1, 550) and (3, 1100) for (x 1, y 1) and (x 2, y 2). Simplify as needed. = 275 3. 3. 3: Recognizing Average Rate of Change 10

Guided Practice: Example 2, continued The rate of change for this function over the interval [1, 3] is approximately $275 per year. ✔ 11 3. 3. 3: Recognizing Average Rate of Change

Guided Practice: Example 2, continued 12 3. 3. 3: Recognizing Average Rate of Change

Guided Practice Example 3 Jasper is curious about how the rate of change differs for the interval [3, 6]. Calculate the rate of change using the graph from Example 2. 13 3. 3. 3: Recognizing Average Rate of Change

Guided Practice: Example 3, continued 1. Determine the interval to be observed. The interval to observe is [3, 6], or where 3 ≤ x ≤ 6. 14 3. 3. 3: Recognizing Average Rate of Change

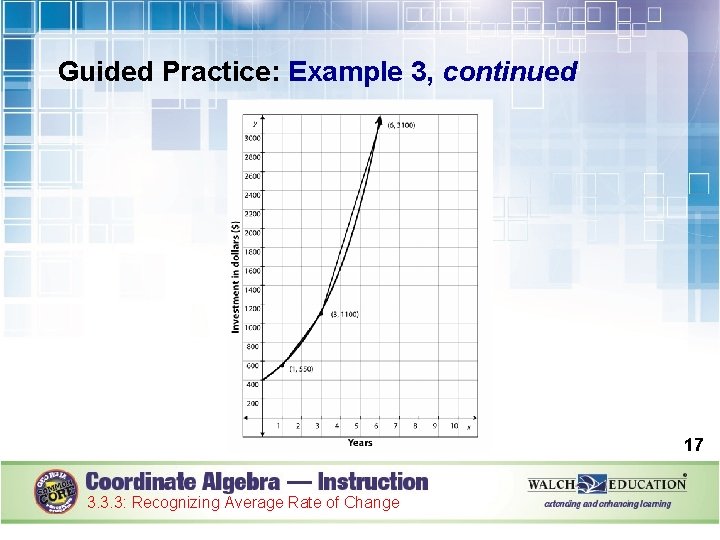
Guided Practice: Example 3, continued 2. Identify the starting point of the interval. The x-value of the starting point is 3. The corresponding y-value is approximately 1, 100. The starting point of the interval is (3, 1100). 15 3. 3. 3: Recognizing Average Rate of Change

Guided Practice: Example 3, continued 3. Identify the ending point of the interval. The x-value for the ending point is 6. The corresponding y-value is approximately 3, 100. The ending point of the interval is (6, 3100). 16 3. 3. 3: Recognizing Average Rate of Change

Guided Practice: Example 3, continued 17 3. 3. 3: Recognizing Average Rate of Change

Guided Practice: Example 3, continued 4. Substitute (3, 1100) and (6, 3100) into the slope formula to calculate the rate of change. Slope formula Substitute (3, 1100) and (6, 3100) for (x 1, y 1) and (x 2, y 2). Simplify as needed. 18 3. 3. 3: Recognizing Average Rate of Change

Guided Practice: Example 3, continued The rate of change for this function over the interval [3, 6] is approximately $666. 67 per year. Notice that the rate of change for the interval [3, 6] is much steeper than that of the interval [1, 3]. ✔ 19 3. 3. 3: Recognizing Average Rate of Change

Guided Practice: Example 3, continued 20 3. 3. 3: Recognizing Average Rate of Change