Introduction precision and accuracy An Archery Example This

Introduction precision and accuracy An Archery Example This presentation is partially animated. Only use the control panel at the bottom of screen to review what you have seen. When using your mouse, make sure you click only when it is within the light blue frame that surrounds each slide. 1

2

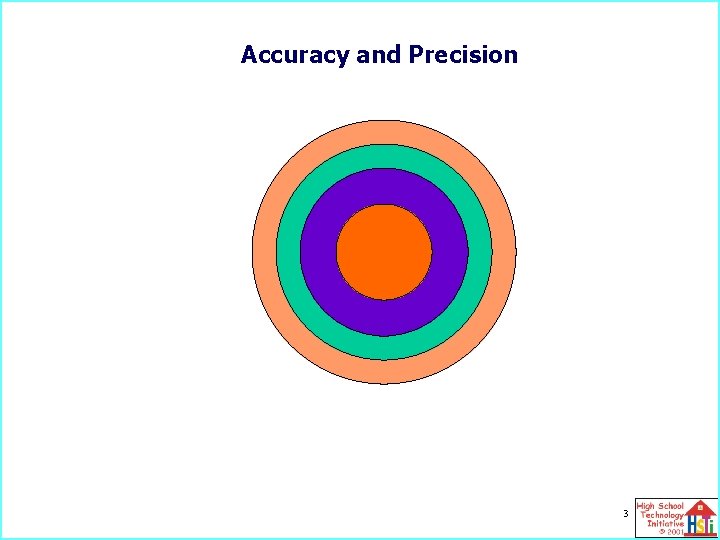
Accuracy and Precision 3

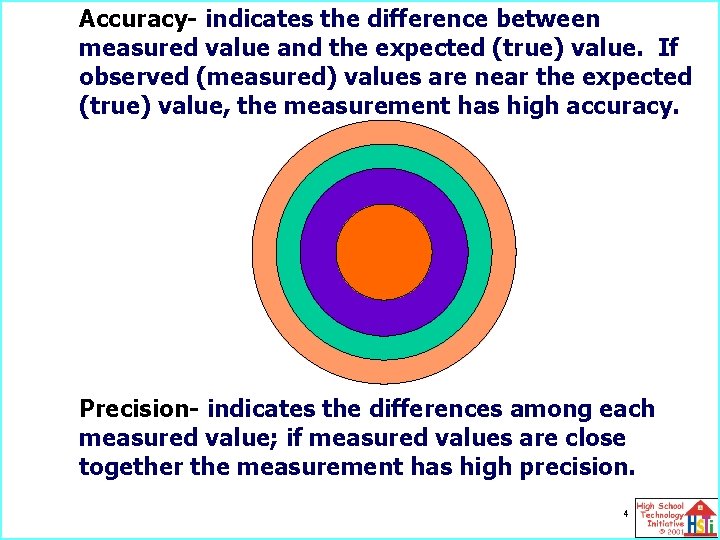
Accuracy- indicates the difference between measured value and the expected (true) value. If observed (measured) values are near the expected (true) value, the measurement has high accuracy. Precision- indicates the differences among each measured value; if measured values are close together the measurement has high precision. 4

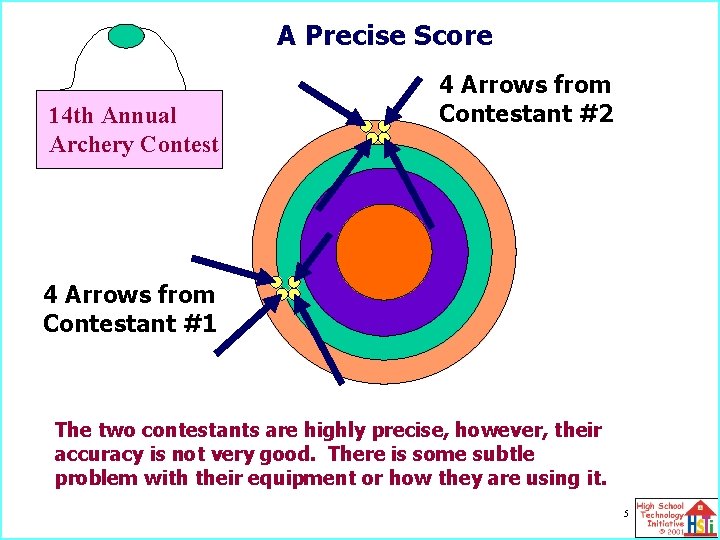
A Precise Score 14 th Annual Archery Contest 4 Arrows from Contestant #2 4 Arrows from Contestant #1 The two contestants are highly precise, however, their accuracy is not very good. There is some subtle problem with their equipment or how they are using it. 5

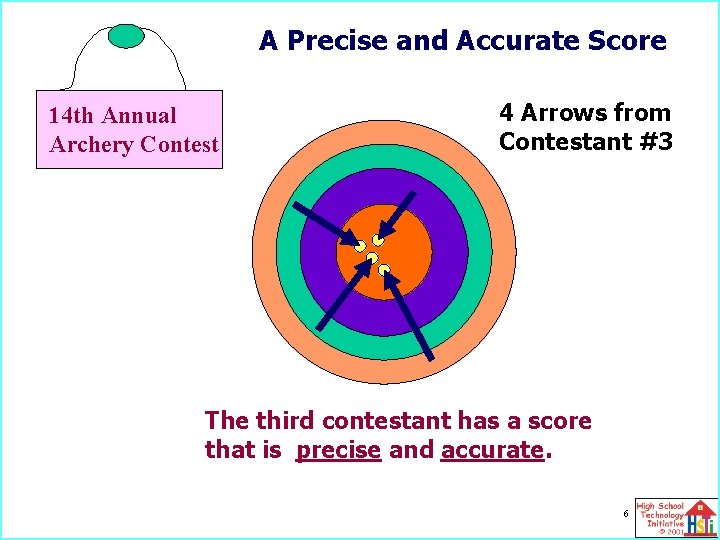
A Precise and Accurate Score 14 th Annual Archery Contest 4 Arrows from Contestant #3 The third contestant has a score that is precise and accurate. 6

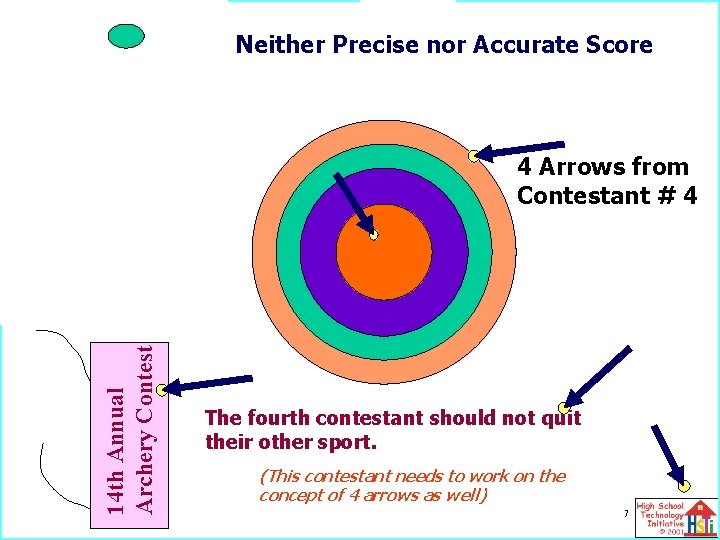
Neither Precise nor Accurate Score 14 th Annual Archery Contest l t 14 th Annualnua ntes n Co A Archery Contest th ery 4 1 ch Ar 4 Arrows from Contestant # 4 The fourth contestant should not quit their other sport. (This contestant needs to work on the concept of 4 arrows as well) 7

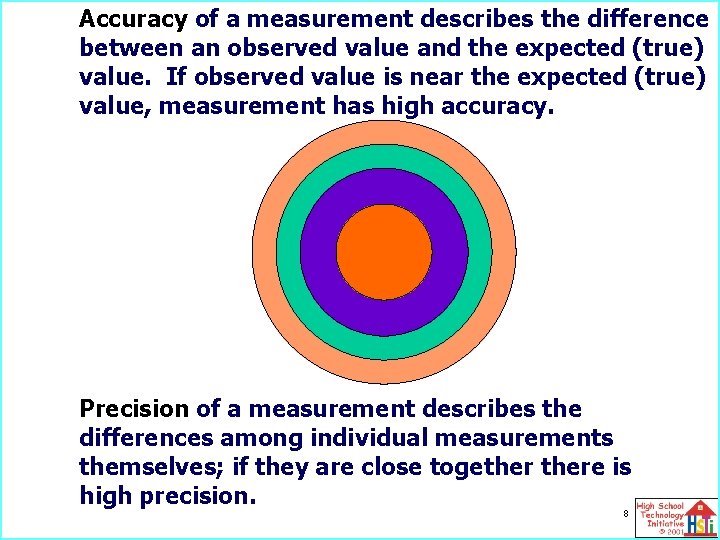
Accuracy of a measurement describes the difference between an observed value and the expected (true) value. If observed value is near the expected (true) value, measurement has high accuracy. Precision of a measurement describes the differences among individual measurements themselves; if they are close togethere is high precision. 8

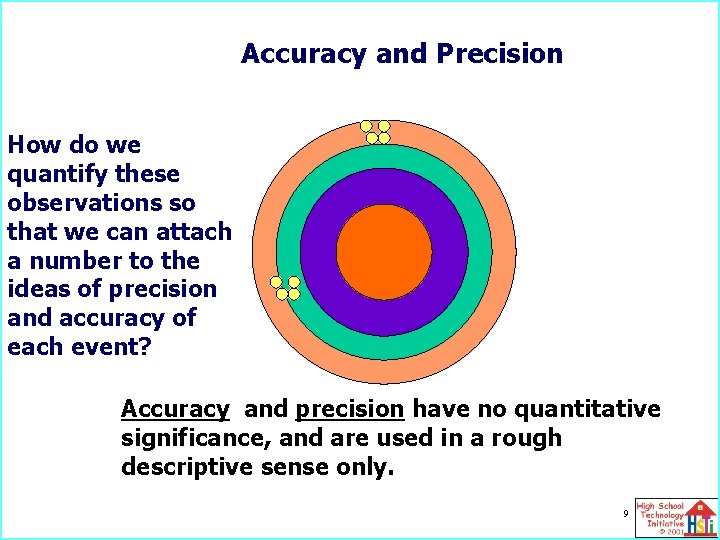
Accuracy and Precision How do we quantify these observations so that we can attach a number to the ideas of precision and accuracy of each event? Accuracy and precision have no quantitative significance, and are used in a rough descriptive sense only. 9

Error and Deviation Error expresses accuracy in the form of a number that relates the measured value to the true (expected) value. Deviation expresses precision in the form of a number that relates the measured value to its closeness to other measured values. 10

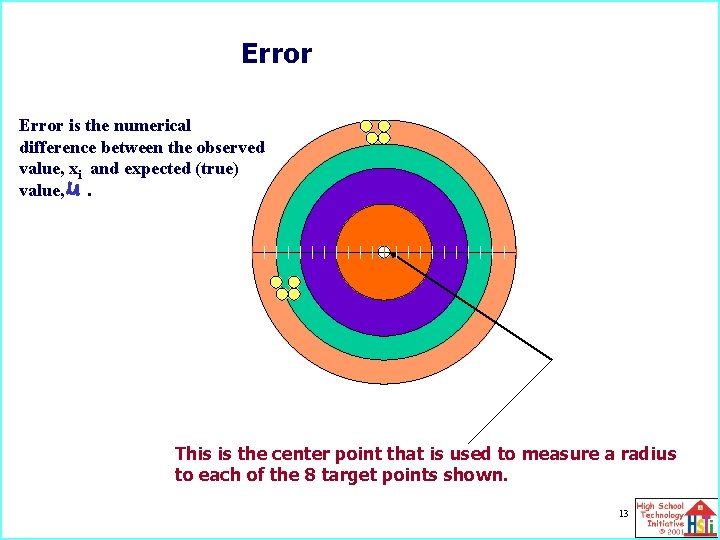
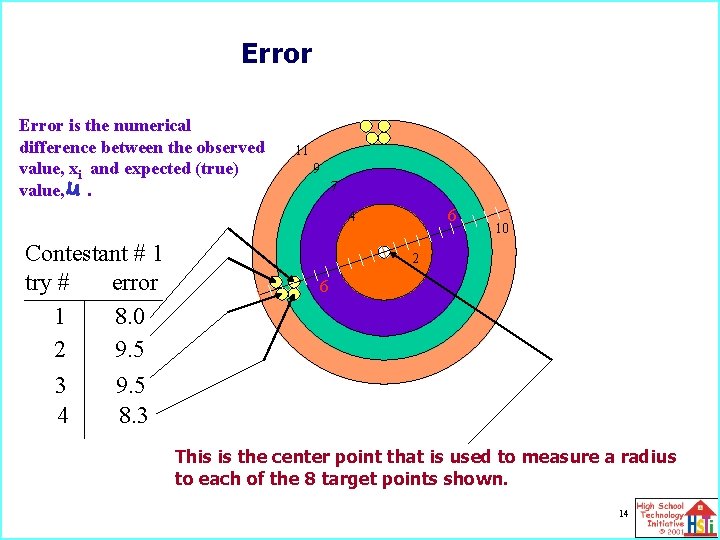
Error expresses accuracy in the form of a number that relates the measured value to the true (expected) value. Error is the numerical difference between the observed value, xi and expected (true) value, . 11

Error is the numerical difference between the observed value, xi and expected (true) value, . For this case, the expected position on the target for the expert is assigned the true (expected) score. This position is assigned a distance value of 0 and distance from this perfect score point on the target to an actual contestant point on the target is the error. 12

Error is the numerical difference between the observed value, xi and expected (true) value, . This is the center point that is used to measure a radius to each of the 8 target points shown. 13

Error is the numerical difference between the observed value, xi and expected (true) value, . 11 9 7 6 4 Contestant # 1 try # error 1 8. 0 2 9. 5 3 9. 5 4 8. 3 10 2 6 This is the center point that is used to measure a radius to each of the 8 target points shown. 14

Contestant # 2 try # error X 5 ? 10. 5 X 6 10. 5 Error In this example, the perfect score, , is equal to zero. A contestant's score, xi, is subtracted from to indicate the error. 11 9 6 7 = perfect score = 0 X 7 X 8 5 9. 5 2 Error Calculation Error =(observed score, xi ) - Contestant # 1 try # error X 1 (8. 0 - 0) = 8. 0 X 2 (9. 5 - 0) = 9. 5 X 3 (9. 5 - 0) = 9. 5 X 4 (8. 3 - 0) = 8. 3 2 6 8 10 X 1 X 2 X 3 X 4 - = 8. 0 -0= 8. 0 = 9. 5 - 0 = 9. 5 = 8. 3 - 0 = 8. 3 X 5 X 6 X 7 X 8 - = 10. 5 -0 =10. 5 = 10. 5 -0 = 10. 5 = 9. 5 - 0 = 9. 5 15

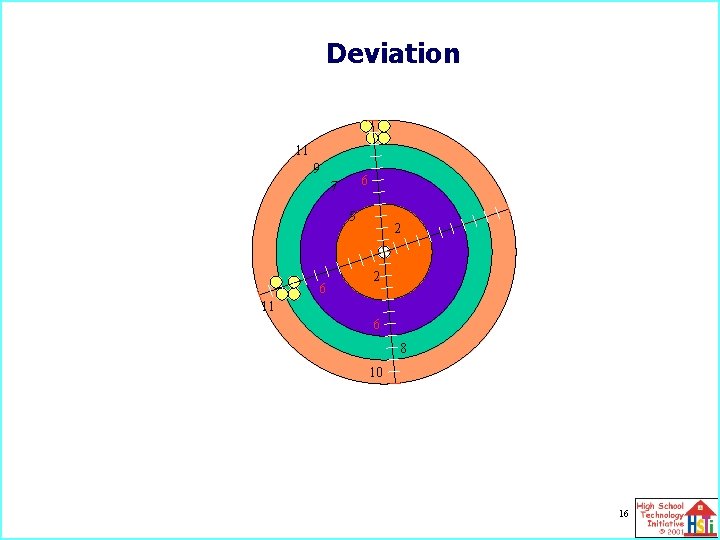
Deviation 11 9 6 7 5 6 2 2 11 6 8 10 16

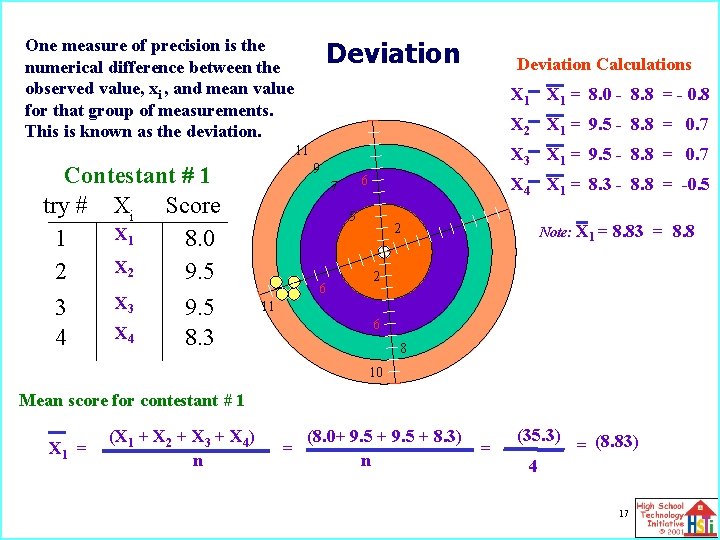
Deviation One measure of precision is the numerical difference between the observed value, xi , and mean value for that group of measurements. This is known as the deviation. Deviation Calculations X 1 = 8. 0 - 8. 8 = - 0. 8 X 2 X 1 = 9. 5 - 8. 8 = 0. 7 11 Contestant # 1 try # Xi Score X 1 1 8. 0 X 2 2 9. 5 X 3 3 9. 5 X 4 4 8. 3 X 1 = 9. 5 - 8. 8 = 0. 7 9 6 7 X 4 X 1 = 8. 3 - 8. 8 = -0. 5 5 6 2 Note: X 1 = 8. 83 = 8. 8 2 11 6 8 10 Mean score for contestant # 1 X 1 = (X 1 + X 2 + X 3 + X 4) n = (8. 0+ 9. 5 + 8. 3) n = (35. 3) = (8. 83) 4 17

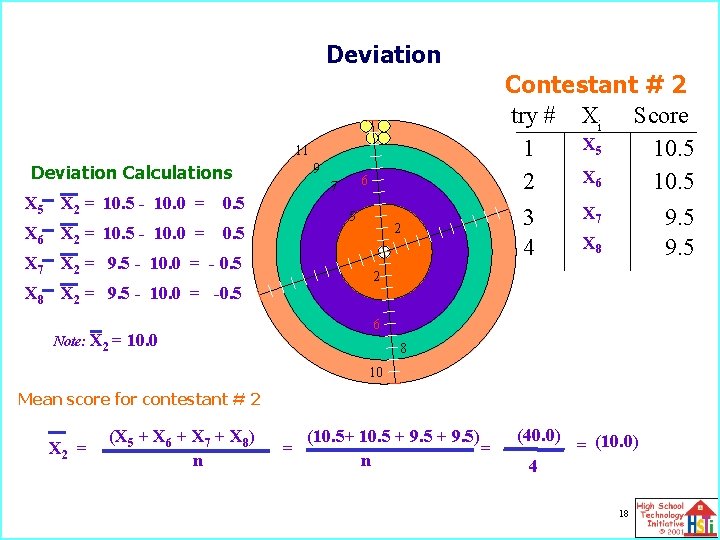
Deviation 11 9 Deviation Calculations X 5 X 2 = 10. 5 - 10. 0 = 0. 5 X 6 X 2 = 10. 5 - 10. 0 = 0. 5 5 X 7 X 2 = 9. 5 - 10. 0 = - 0. 5 2 2 X 8 X 2 = 9. 5 - 10. 0 = -0. 5 Note: 6 7 Contestant # 2 try # Xi Score X 5 1 10. 5 X 6 2 10. 5 X 7 3 9. 5 X 8 4 9. 5 6 X 2 = 10. 0 8 10 Mean score for contestant # 2 X 2 = (X 5 + X 6 + X 7 + X 8) n = (10. 5+ 10. 5 + 9. 5) = n (40. 0) = (10. 0) 4 18

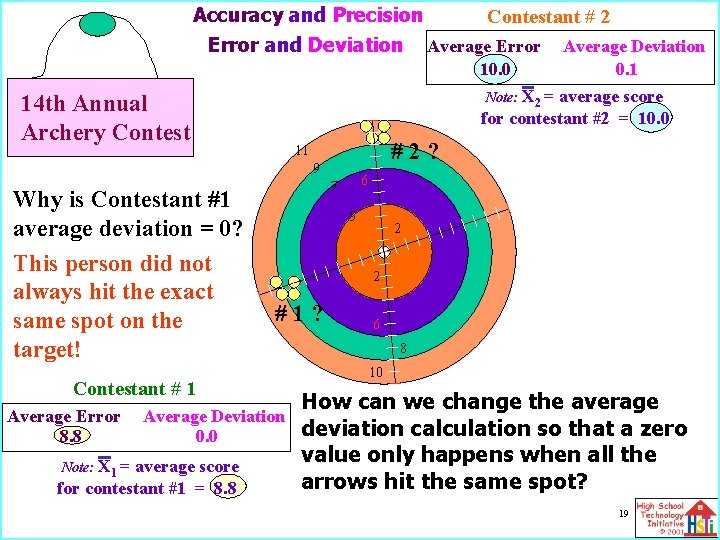
Accuracy and Precision Error and Deviation 14 th Annual Archery Contestant # 1 Average Error 10. 0 Average Deviation 0. 1 X 2 = average score for contestant #2 = 10. 0 Note: #2? 11 9 Why is Contestant #1 average deviation = 0? This Who personwon? did not always hit the exact same spot on the target! Contestant # 2 6 7 5 2 Why? 2 #1? 6 8 Which contestant is a better archer? 10 average equal How. Why can are we the change the scores average Average Error Average Deviation to the calculation average errors? deviation so that a zero 8. 8 0. 0 value only happens when all the Note: X 1 = average score Doeshit that always happen? arrows the same spot? for contestant #1 = 8. 8 19

Accuracy and Precision ( a quick concept review) 20

Accuracy and Precision ( a quick concept review) 21

Accuracy and Precision ( a quick concept review) An example for Accuracy or Precision? An example for Error or Deviation? 22

Accuracy and Precision ( a quick concept review) 23

Accuracy and Precision ( a quick concept review) An example for Accuracy or Precision? An example for Error or Deviation? 24

25

26