Introduction Outline n n n n The Problem

Introduction Outline n n n n The Problem Domain Network Design Spanning Trees Steiner Trees Triangulation Technique Spanners Application Simple Greedy Algorithm

Introduction Outline n The Problem Domain n Network Design n Spanning Trees n Steiner Trees n Triangulation Technique n Spanners Application n Simple Greedy Algorithm

The Problem Domain n General network design problem: Given a set S of n points in Rd, how to construct a good network that connects these points ?

n Property 1: Any network connecting a set of n points must have at least n-1 edges. Sparse network – the number of edges is linear to the number of points. (i. e. O(n) edges)

Introduction Outline n The Problem Domain n Network Design n Spanning Trees Steiner Trees Triangulation Technique Spanners Application Simple Greedy Algorithm n n n

Network Design Network quality measures: n Size Weight n Stretch factor n Degree n Diameter n Connectivity - Fault Tolerance n

Network quality measures (cont. ) n Number of Steiner points n Load Factor (To be covered) e Bottle Neck

Motivation by examples n Scandinavian rail network (prior 2000) Copenhagen Malmo

Motivation by examples n Stretch Factor Imagine set of highways connecting cities. We need to upgrade the highway system in the cost-effective manner. Upgrade carefully selected subset? Should weonly upgrade ALL existing highways of existing highways !

Significance of Network Analysis Queries examples: What isedge thepair size, weight, stretch factor, Which (orof. Klength edges) should bethe added What is the total ofof the edges tofactor be tois For which farthest the pair cites the cites stretch in diameter, degree or connectivity the network achieve greatest decrease added to ? the network tothe achieve aofdesired network largest ? to network ? in the stretch factor and/or factor load factor ? fault-tolerance and stretch without destroying the planarity ?

Network Design Tradeoffs n Bounded degree vs. the small diameter n Small stretch factor vs. the small size/weight Thus, network quality measures can be thought of as multicriteria optimization problems

Introduction Outline n n The Problem Domain Network Design n Spanning Trees n Steiner Trees n Triangulation Technique n Spanners Application n Simple Greedy Algorithm

Spanning Trees n Spanning Tree: given set S of n points, ST(S) is an acyclic connected graph on these points. ¨ Spanning tree is good in sense that it has minimum number of edges ¨ n Sylvester(1857), Cayley(1889) formula: A set of n points has exactly nn-2 spanning trees

Spanning Trees n Let T be a spanning tree of the set S. ωt(T) is defined to be the sum of the length of its edges ¨ Weight ¨ length of an edge {p, q} is the Euclidian distance |pq| between p and q Minimum Spanning Tree - MST(S) of set S is a spanning tree of minimum weight.

MST Properties n Let S be a set of n points in the plane, then: ¨ A MST(S) is a shortest network connecting the points of S ¨ In MST(S), each point has degree at most 6.

Introduction Outline n The Problem Domain Network Design Spanning Trees n Steiner Trees n Triangulation Technique Spanners Application Simple Greedy Algorithm n n n

Steiner Trees n Interconnect set S of points by a network (graph) of shortest length, where the length is the sum of the lengths of all edges. MST…? n We allow additional points (Steiner points) to be added to the graph, in order to reduce the total length n We define: ¨ Steiner Minimum Tree - SMT(S) be a graph with minimum total length(weight)

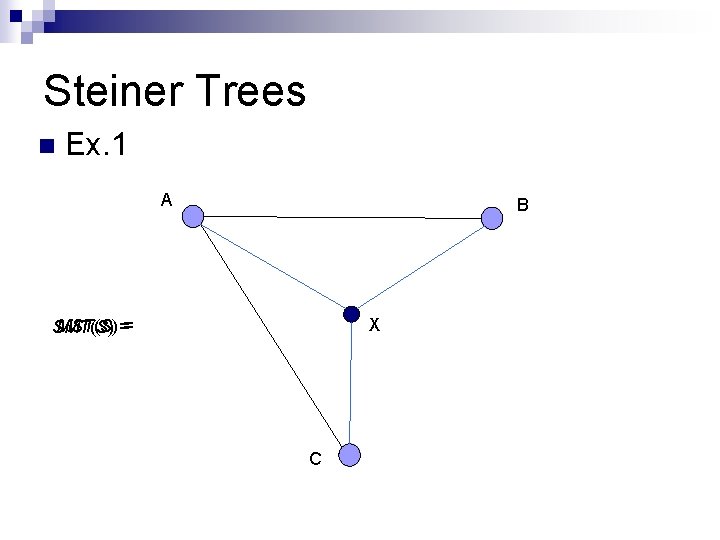
Steiner Trees n Ex. 1 A B X MST(S) == SMT(S) C

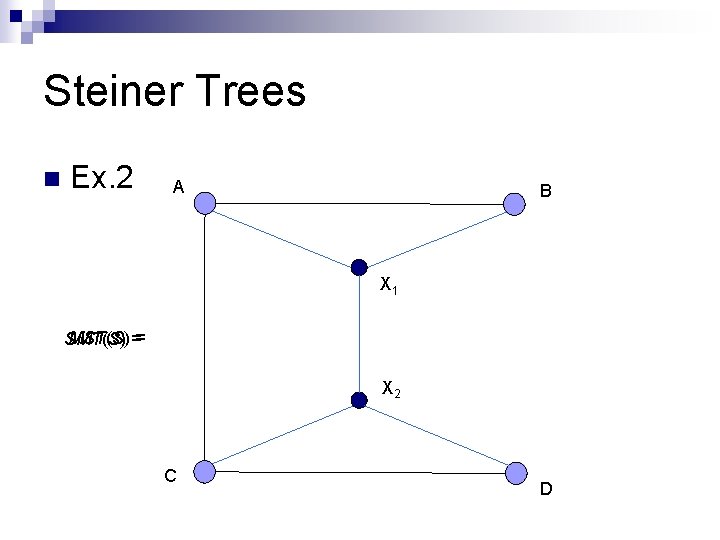
Steiner Trees n Ex. 2 A B X 1 MST(S) == SMT(S) X 2 C D

Steiner Trees n Lemma (1. 1. 4) ¨ Let S be a finite set of points in Rd, then: ωt(MST(S)) ≤ n 2 ∘ ωt(SMT(S)) Proof : Let : SMT(S)=T we will construct a spanning tree T* of S having at most twice the weight of T

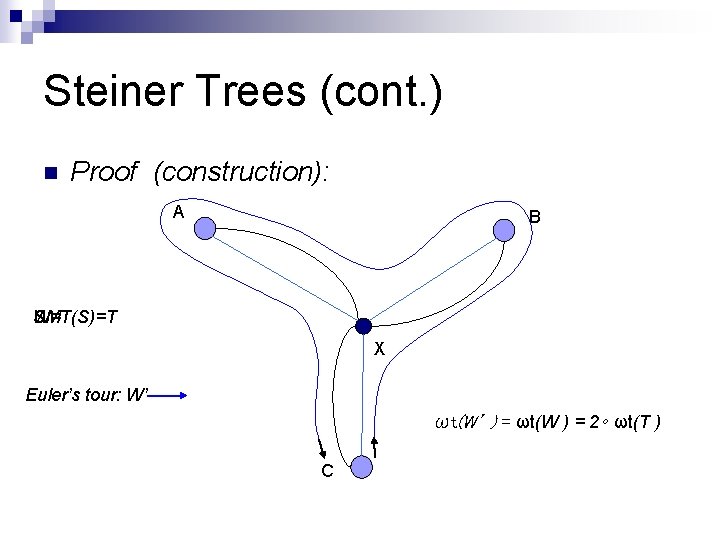
Steiner Trees (cont. ) n Proof (construction): A B SMT(S)=T W= X Euler’s tour: W’ ωt(W’ ) = ωt(W ) = 2∘ ωt(T ) C

Steiner Trees (cont. ) n We will construct T* of points of S from W’ (Euler’s tour) applying the short-cuts technique: ¨ remove all Steiner points ¨ For each point p of S, remove all visits to p except the first one n As result we have: ¨ T* that visits each point of S exactly once ¨ ωt(T*) ≤ 2∘ωt(T)

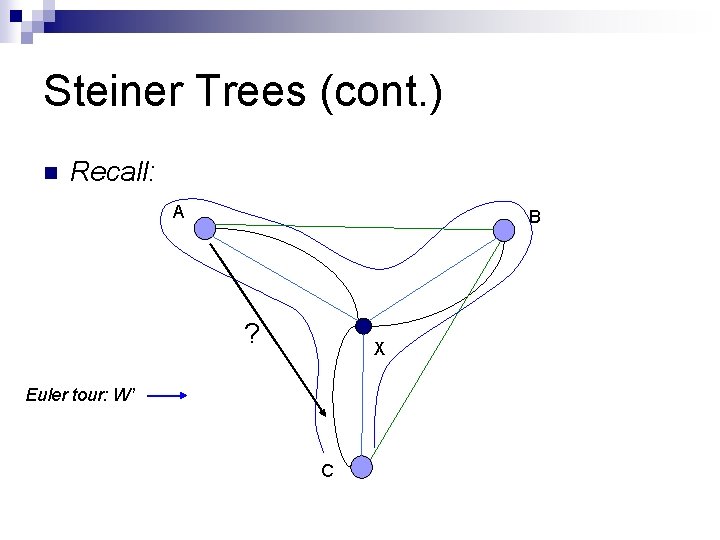
Steiner Trees (cont. ) n Recall: A B ? X Euler tour: W’ C

Steiner Trees (cont. ) n Is factor 2 is the best possible…? n Gilbert & Pollack (1968) conjectured that: ¨ n is the best possible That is, for any finite set S of points of R 2 : ωt(MST(S)) ≤ ∘ ωt(SMT(S)) After 20 years, Du&Hwang settled the conjecture

Introduction Outline n The Problem Domain Network Design Spanning Trees Steiner Trees n Triangulation Technique n Spanners Application Simple Greedy Algorithm n n n

Triangulation n Define: Convex Hull of set of points S in a real vector space V is the minimal Convex Set containing S In Euclidian Space, an object is convex if : for every pair of points within the object, every point on the straight line segment that joins them is also within the object A Convex set A non-Convex set X X Y Y

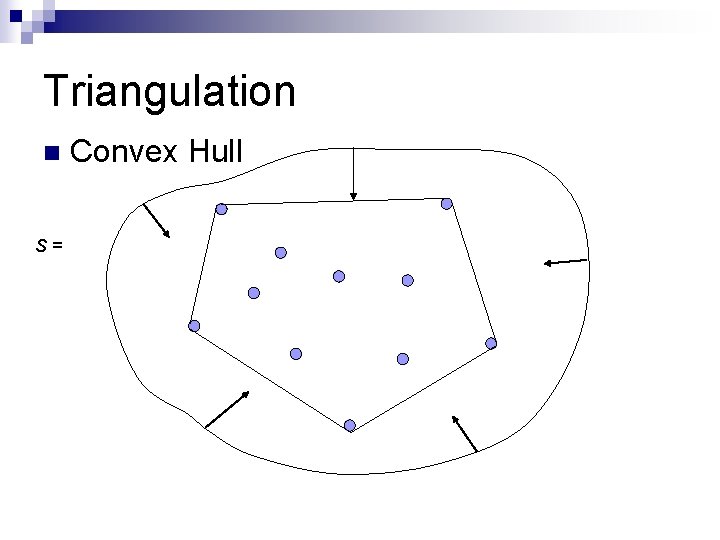
Triangulation n S= Convex Hull

Triangulation n General: ¨ Subdivision n of geometric object into simplices In particular: ¨ In the plane it is a subdivision into triangles, hence the name. n Let S be a set of points in the plane ¨A triangulation is a partition of the convex hull into triangles , such that vertices of these triangles are exactly points of S

Triangulation n Ex. 3 S=

Delaunay Triangulation n Boris Delaunay (1934) n Delaunay triangulation for a set S of points in the plane is a triangulation DT(S) that: ¨ n no point of S, is inside the circumcircle of any triangle in DT(S) Property: ¨ DT(S) contains MST(S)

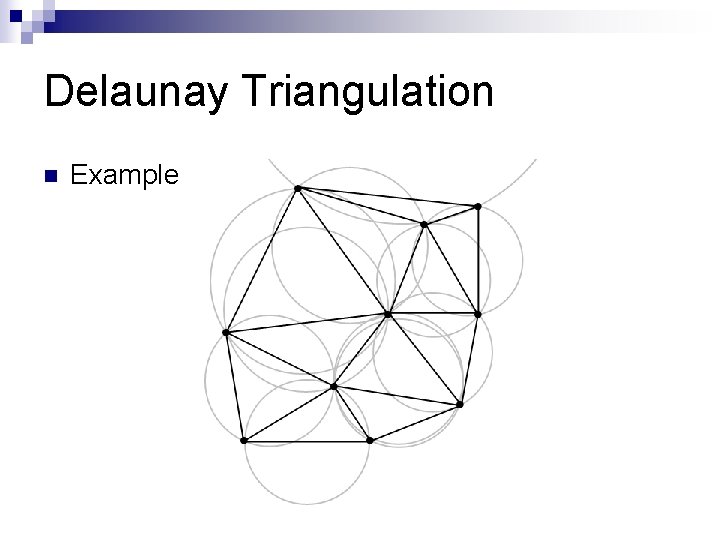
Delaunay Triangulation n Example

Introduction Outline n The Problem Domain Network Design Spanning Trees Steiner Trees Triangulation Technique n Spanners Application Simple Greedy Algorithm n n n

Spanners n Spanner Definition. Let S be a set of n points in Rd and let t ≥ 1 be a real number. A t-spanner for S is an undirected graph G with vertex set S, such that for any two points p and q of S, there is a path in G between p and q, whose length is less than or equal to t|pq|. Any path satisfying this condition is called a t-spanner path between p and q.

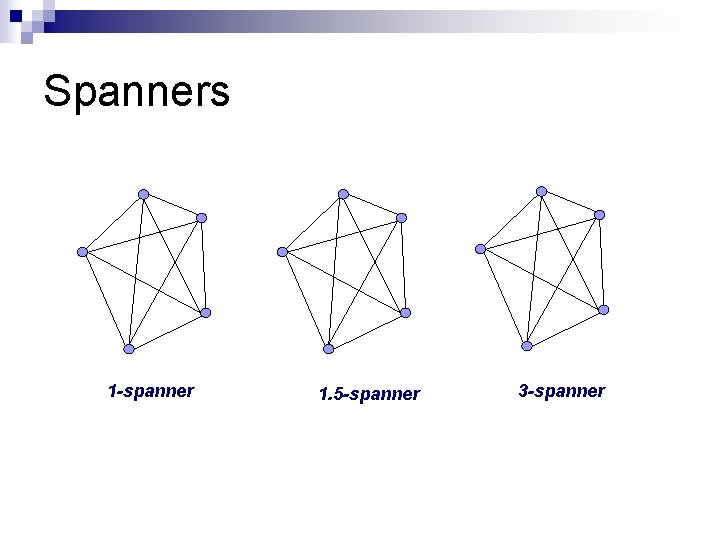
Spanners 1 -spanner 1. 5 -spanner 3 -spanner

Spanners n Stretch Factor Definition. Let S be a set of n points in Rd and let G be a Euclidean graph with vertex set S. The stretch factor of G is the smallest real number t such that G is a t-spanner of S.

Spanners n Spanner Property. Let S be a set of n points in Rd and let t ≥ 1 be a real number. Any t-spanner of S has: 1. 2. Number of edges - at least n – 1 Weight - at least ωt(MST(S))

Spanners n Basic Spanner Problem Let S be a set of n points in Rd and let t ≥ 1 be a real number. Does there exist a t-spanner for S having at most ctdn edges, where ctd is a real number that depends only on t and d? If so, how much time does it take to compute such a t-spanner?

Introduction Outline n The Problem Domain Network Design Spanning Trees Steiner Trees Triangulation Technique Spanners n Spanners Application n Simple Greedy Algorithm n n n

Spanners Application n Approximating Minimum Spanner Trees Let S be a set of n points in the plane. Since any MST(S) of S is contained in Delanay triangulation DT(S) of S, we can compute MST(S) in the following way: 1. Compute DT(S) in O(n log n) time. 2. Compute MST of DT(S), which is in fact an Euclidean MST of the set S. Since DT(S) contains only linear number of edges, entire algorithm runs O(n log n)

Theorem Let S be a set of n points in Rd, let t ≥ 1 be a real number and let G be an arbitrary tspanner for S. A minimum spanning tree of G is t-approximate minimum spanning tree of S, that is the weight of any MST of G is at most t∘ωt(MST(S))

Proof n Let T be a minimum spanning tree of S, and number its edges arbitrarily as e 1, e 2, …en-1. Consider edge ei. Since G is a t-spanner for S, there exists a t-spanner path Pi in G between the endpoints of ei. Thus the length wt(Pi) of Pi is at most t times the length of ei. It follows that:

Proof (cont. ) n Let G’ be the subgraph of G, whose edge set is the union of the edge sets of the paths Pi, 1 ≤ i ≤ n-1. Then G’ is a connected graph with vertex set S and its weight is at most t*wt(MST(S)). Since the weight of the minimum spanning tree of G is less than of equal to the weight of G’, the proof is complete.

Introduction Outline n The Problem Domain Network Design Spanning Trees Steiner Trees Triangulation Technique Spanners Application n Simple Greedy Algorithm n n n

Greedy Spanner Algorithm Path. Greedy (S, t) Input: Set S of n points in Rd , t > 1 Output: G=(S, E) – a t-spanner for S n n Sort the ( ) pairs of distinct points in nondecreasing order of their distances and store them in list L E {} G (S, E) for each pair (u, v) є L (considering pairs in sorted order) let d. G(u, v) be the length of the shortest path in G between u and v ¨ if d. G(u, v) > t |u, v| n add (u, v) to E ¨ n Output G

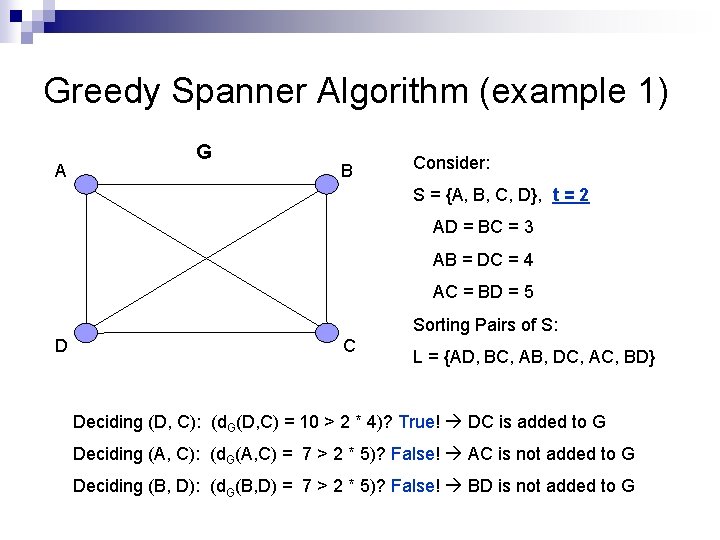
Greedy Spanner Algorithm (example 1) A G B Consider: S = {A, B, C, D}, t = 2 AD = BC = 3 AB = DC = 4 AC = BD = 5 Sorting Pairs of S: D C L = {AD, BC, AB, DC, AC, BD} Deciding (D, C): (d. G(D, C) = 10 > 2 * 4)? True! DC is added to G Deciding (A, C): (d. G(A, C) = 7 > 2 * 5)? False! AC is not added to G Deciding (B, D): (d. G(B, D) = 7 > 2 * 5)? False! BD is not added to G

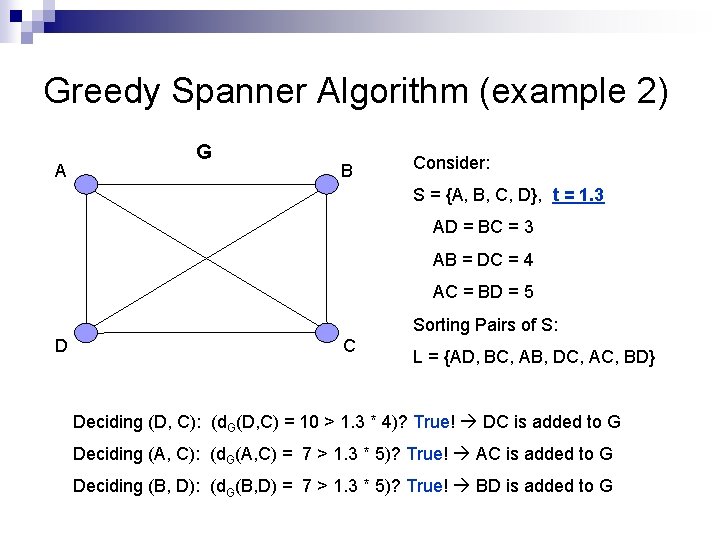
Greedy Spanner Algorithm (example 2) A G B Consider: S = {A, B, C, D}, t = 1. 3 AD = BC = 3 AB = DC = 4 AC = BD = 5 Sorting Pairs of S: D C L = {AD, BC, AB, DC, AC, BD} Deciding (D, C): (d. G(D, C) = 10 > 1. 3 * 4)? True! DC is added to G Deciding (A, C): (d. G(A, C) = 7 > 1. 3 * 5)? True! AC is added to G Deciding (B, D): (d. G(B, D) = 7 > 1. 3 * 5)? True! BD is added to G