Introduction of Applied Finite Element Method Dr Om

Introduction of Applied Finite Element Method Dr. Om Prakash Singh Asst. Prof. , IIT Mandi www. omprakashsingh. com

Course Policy • Contact Hours: 1. 5 hour lectures, 1. 5 hours lab • Credits: 3 • Assessment: – – – Quizzes - 50 min: 2 x 15 = 30 marks Technical publication in Wikipedia: 20 marks Assignments: 20 marks End Exam- 3 hrs: 20 marks (online) Attendance: 10 marks • Books 1. Practical Finite Element Analysis by Nitin Gokhle, Deshpande, Bedekar and Thite; Rs 700 2. Textbook of Finite Element Analysis by P. Seshu; Rs 300 3. Finite Element Analysis by Udai Borker Rs 400 4. Buy one more book after discussion with other faculty

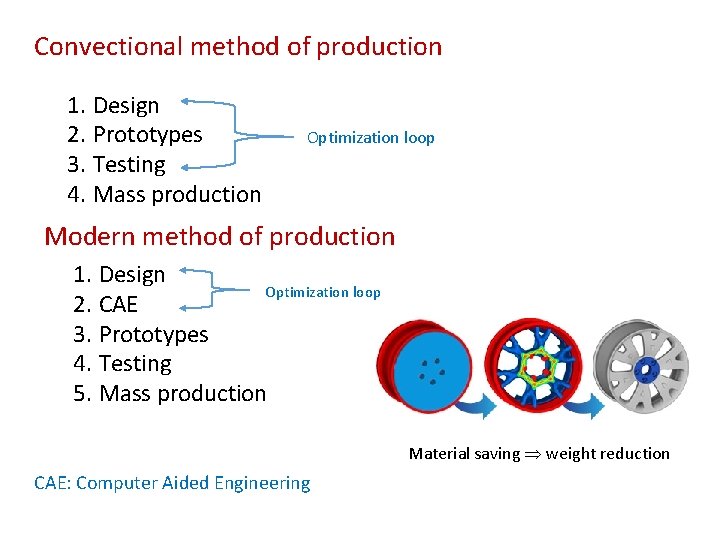
Convectional method of production 1. Design 2. Prototypes 3. Testing 4. Mass production Optimization loop Modern method of production 1. Design Optimization loop 2. CAE 3. Prototypes 4. Testing 5. Mass production Material saving weight reduction CAE: Computer Aided Engineering

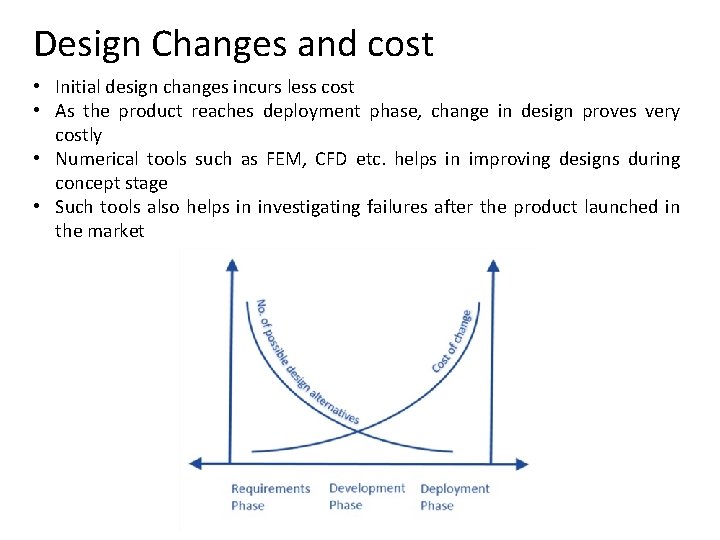
Design Changes and cost • Initial design changes incurs less cost • As the product reaches deployment phase, change in design proves very costly • Numerical tools such as FEM, CFD etc. helps in improving designs during concept stage • Such tools also helps in investigating failures after the product launched in the market

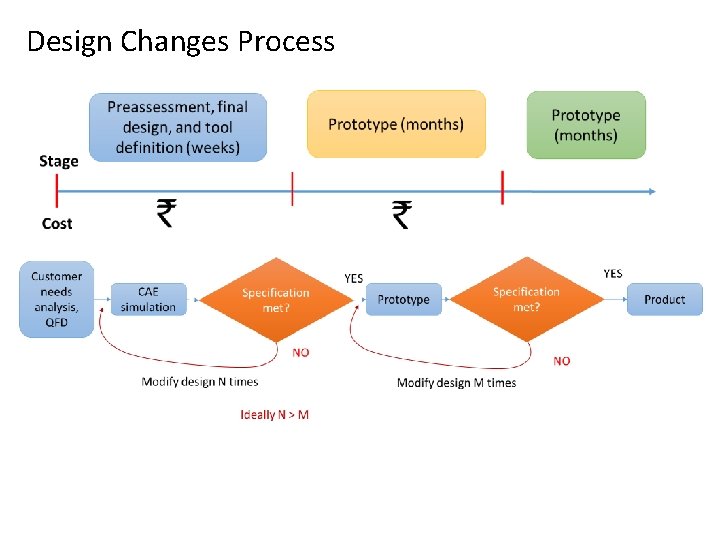
Design Changes Process

Finite Element Analysis (FEA) or Finite Element Method (FEM) • The Finite Element Analysis (FEA) is a numerical method for solving problems of engineering and mathematical physics. • Useful for problems with complicated geometries, loadings, and material properties where analytical solutions can not be obtained

The Purpose of FEA Analytical Solution • • Stress analysis for trusses, beams, and other simple structures are carried out based on dramatic simplification and idealization: – mass concentrated at the center of gravity. – beam simplified as a line segment (same cross-section). Design is based on the calculation results of the idealized structure & a large safety factor (1. 5 -3) given by experience. FEA • Design geometry is a lot more complex; and the accuracy requirement is a lot higher. We need – To understand the physical behaviors of a complex object (strength, heat transfer capability, fluid flow, etc. ) – To predict the performance and behavior of the design; to calculate the safety margin; and to identify the weakness of the design accurately; and – To identify the optimal design with confidence

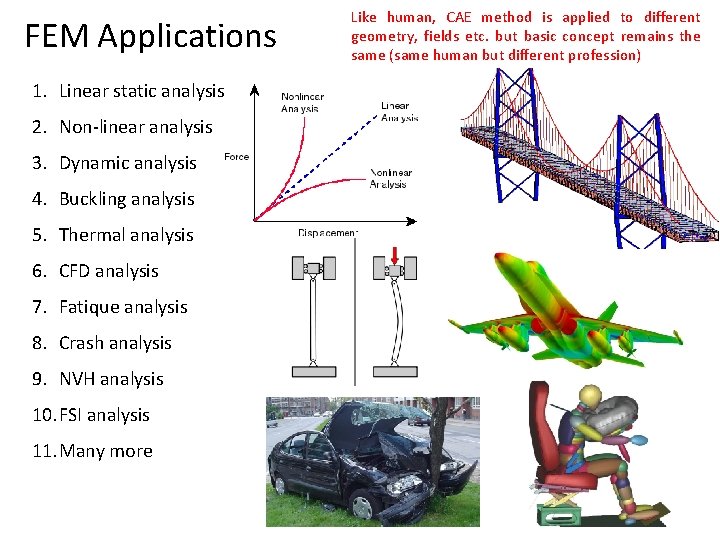
FEM Applications 1. Linear static analysis 2. Non-linear analysis 3. Dynamic analysis 4. Buckling analysis 5. Thermal analysis 6. CFD analysis 7. Fatique analysis 8. Crash analysis 9. NVH analysis 10. FSI analysis 11. Many more Like human, CAE method is applied to different geometry, fields etc. but basic concept remains the same (same human but different profession)

What is degree of freedom (dof)? • The minimum number of parameters (motion, coordinates, temp. etc. ) required to define the position of any entity completely in the space is known as a degree of freedom (dof). • In 2 -D (planar) problem, only two values of x and y coordinates are needed to define the new position B of the object. Hence 2 dof (translation x and y) • The point A is a part of a line, now one angle should also be defined in addition to the two translations i. e. 3 dofs (two translations and one rotation). • If the points A and B are shifted out of the plane and the line is rotated arbitrarily with respect to all of the three axes. The minimum number of parameters to define the position of point A completely would be 6 dofs (3 translations (Ux, Uy, Uz ) and 3 rotations (θx , θy , θz ). • The total dofs for a given mesh model is equal to the number of nodes multiplied by the number of dof per node. • If analysis is only for temperature, dof is one (temperature) A B B A

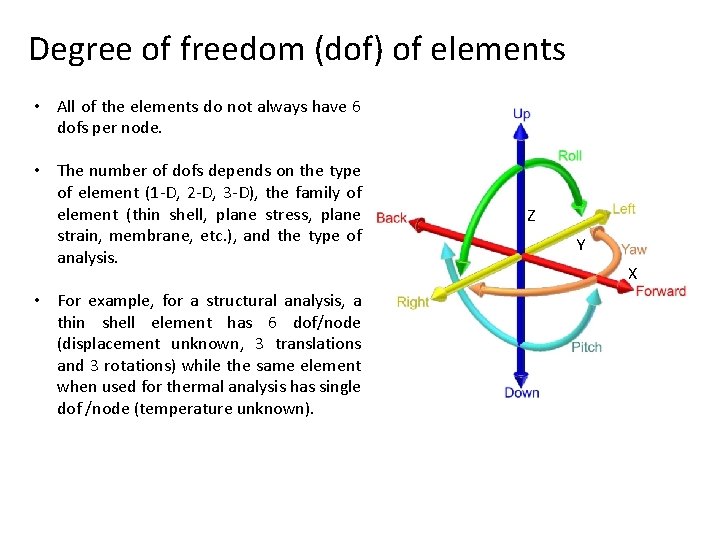
Degree of freedom (dof) of elements • All of the elements do not always have 6 dofs per node. • The number of dofs depends on the type of element (1 -D, 2 -D, 3 -D), the family of element (thin shell, plane stress, plane strain, membrane, etc. ), and the type of analysis. • For example, for a structural analysis, a thin shell element has 6 dof/node (displacement unknown, 3 translations and 3 rotations) while the same element when used for thermal analysis has single dof /node (temperature unknown). Z Y X

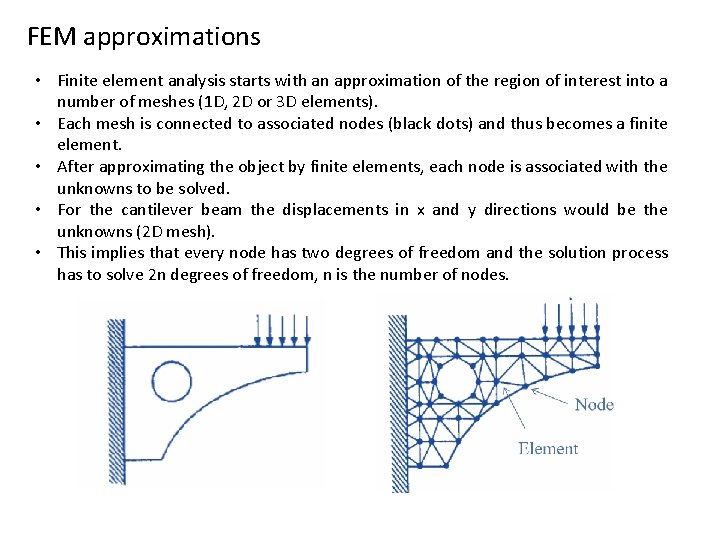
FEM approximations • Finite element analysis starts with an approximation of the region of interest into a number of meshes (1 D, 2 D or 3 D elements). • Each mesh is connected to associated nodes (black dots) and thus becomes a finite element. • After approximating the object by finite elements, each node is associated with the unknowns to be solved. • For the cantilever beam the displacements in x and y directions would be the unknowns (2 D mesh). • This implies that every node has two degrees of freedom and the solution process has to solve 2 n degrees of freedom, n is the number of nodes.

Why meshing is done? Node Element • No. of points = (infinite) • dof per points = 6 ( a point can move 6 ways) • Total equations = 6 = • Solving time = (impossible) • • No. of nodes = 700 (finite) dof per nodes = 6 Total equations = 700 6 = 4200 Solving time = finite • FEM/CFD or any numerical techniques reduced infinite degrees of freedom to finite dof with the help of discretization • Obtain a set of algebraic equations to solve for unknown (first) nodal quantity (displacement/temperature etc. ) • Secondary quantities (stresses and strains) are expressed in terms of nodal values of primary quantity Object

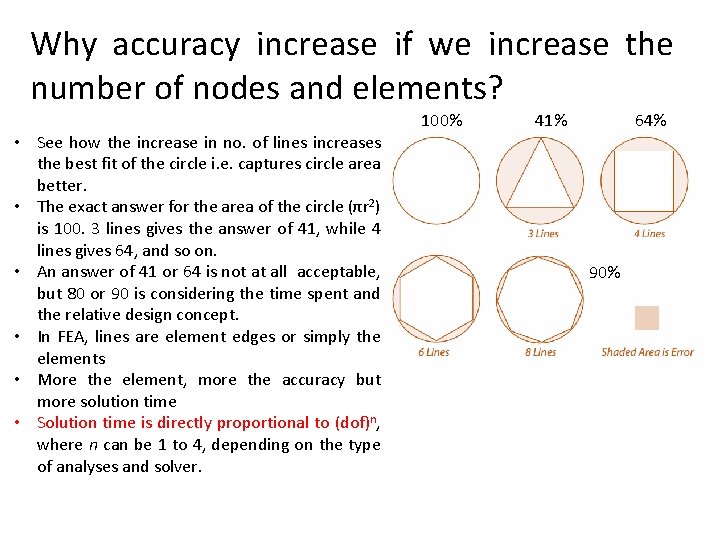
Why accuracy increase if we increase the number of nodes and elements? • See how the increase in no. of lines increases the best fit of the circle i. e. captures circle area better. • The exact answer for the area of the circle (πr 2) is 100. 3 lines gives the answer of 41, while 4 lines gives 64, and so on. • An answer of 41 or 64 is not at all acceptable, but 80 or 90 is considering the time spent and the relative design concept. • In FEA, lines are element edges or simply the elements • More the element, more the accuracy but more solution time • Solution time is directly proportional to (dof)n, where n can be 1 to 4, depending on the type of analyses and solver. 100% 41% 64% 90%

Types of Geometry and Element • Ideally, all physical objects have three dimension • In FEA, we represent objects into 1 D, 2 D and 3 D types for ease of doing analysis 1 D wire • rod, bar, beam, pipe etc. type elements • x >> y, x • Real constraint: c/s area needed 2 D plate • thin shell, membrane, plane strain, plain stress etc. type elements • x, y >> z • Thickness needed 3 D wall • tetra, penta, hex, pyramid etc. type elements • x y z • No geometry info needed Wired Bridge Human • 0 D element; • concentrated mass element at CG)

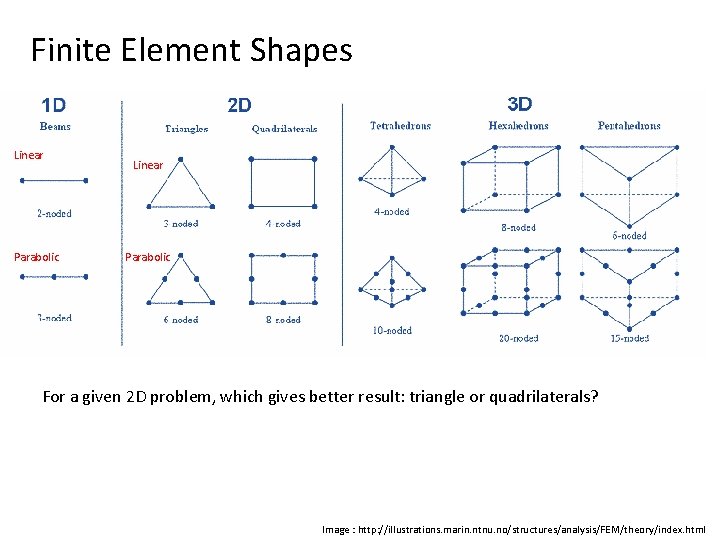
Finite Element Shapes Linear Parabolic For a given 2 D problem, which gives better result: triangle or quadrilaterals? Image : http: //illustrations. marin. ntnu. no/structures/analysis/FEM/theory/index. html

Can we solve same problem using 1 D, 2 D or 3 D element? Yes Any analysis method should give the same results However, computational time and effort varies If a 1 D problem (e. g. truss in bridges) is solved using 3 D elements, number of elements and hence degree of freedom will be prohibitively large. • For simple geometries, it does not really matter how analysis is done but for large complex geometries such as bridges, buildings, full vehicle etc. identification of geometry into 1 D, 2 D and 3 D must be done • •

Equation of motions (solid body, conserves forces) Or When, …. (1)

Equation of motions (Fluid, conserves forces) • Two-dimensional momentum equation for fluid flow given below. • Nature of equation for fluid flow is same as that of solids. • Fluid cannot withstand shear, hence no internal resistance. Inertia force Viscous dissipation External pressure force • In the above equation, u is the velocity = dx/dt • Equation of motion solving techniques are different for solid and fluids • Same equation can be solved using FEM or FVM (finite volume method) or any other method. • However, the final results should be same irrespective of solution methods • For solid bodies, FEM preferred over FVM is preferred for solving fluid flow equations.

Final form of solution • If the equation of motion (solid or fluid) are solved numerically (FEM, FVM etc), the final form of solution has the matrix form as • Above form remains the same regardless of the type of problem, the complexity of the element, or the way in which the element properties were derived. • K is the stiffness matrix which contains information about the geometry, material or fluid properties etc. • F is the matrix contains boundary condition informations such as applied force, known displacement applied on the structure, known boundary temperature etc. • U is the primary variable which needs to be determined. U can be displacement, velocity, temperature etc. depending upon the equation solved. • The matrix has to be inverted to get x. • Different strategies are adopted to invert the matrix e. g. TDMA, Gauessian elimination etc. • Once U is known, other secondary parameters such as gradients, stresses etc. can be further derived.

Matrix equation: One dimensional heat flow Nodal heat flow entering the a typical node in the terms of nodal temperature is given by And since conservation of energy requires Q 2 = -Q 1, In matrix notation, above two equations can be expressed as In concise form

Matrix equation: Linear Spring systems • According to Hook’s law, when an elastic spring experiences an axial load F, it deflects an amount , given by k 1 k 2 2 • Where k is the spring stiffness (spring constant) • Nodal force F 1 in terms of nodal displacement for the above spring system can be written in the form • And since equilibrium of forces requires F 2 = -F 1 • In matrix notation, Or x

Matrix equation: Fluid flow Q, For a circular pipe with constant cross- P 1 1 sectional, fully developed laminar flow with no losses, the volume flow rate Q is related to pressure gradient as 1 2 Where is the dynamic viscosity of the fluid, and D is the pipe diameter. For a typical element of length of L, we may write, Where P is the pressure drop over a length L. We can express the nodal volume flow rate at 1 as , and since conservation mass requires Q 2 = -Q 1 , In matrix form, Or Q 2, P 2

Consistent unit input in software • Some software does not understand units • Geometry in mm is preferable as it gives larger surface area per unit mesh length • If geometry is in mm, then not the followings: • 1 N = 1 kg * 1 m/s 2 (F = m*a) • 1 N = 1 kg * 1000 mm/s 2 • 1 N = 1000 kg * 1 mm/s 2 • 1 N = 1 tonne * 1 mm/s 2 • Hence, geometry size is in mm and force in Newton then mass must be specified in tonne and density in tonne/mm 3 Geometry in meter Geometry in mm (scale by 1000)

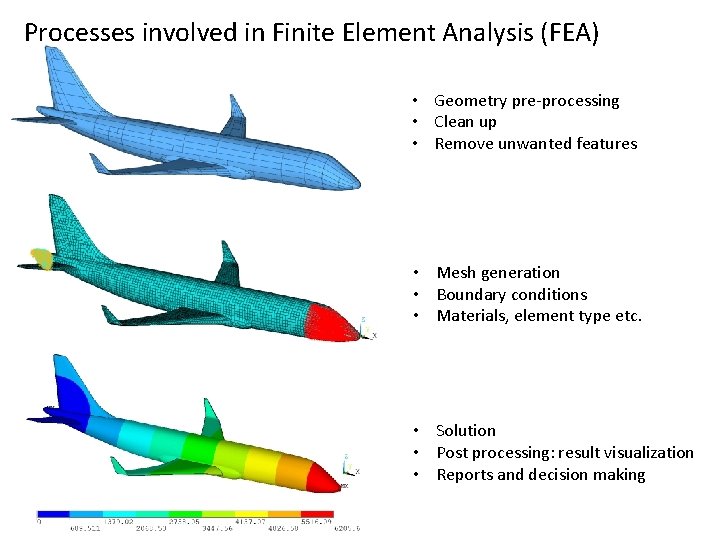
Processes involved in Finite Element Analysis (FEA) • Geometry pre-processing • Clean up • Remove unwanted features • Mesh generation • Boundary conditions • Materials, element type etc. • Solution • Post processing: result visualization • Reports and decision making

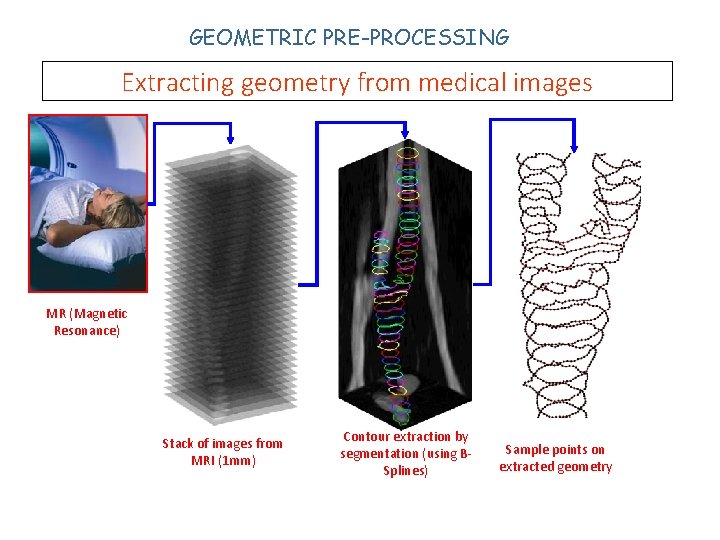
GEOMETRIC PRE-PROCESSING Extracting geometry from medical images MR (Magnetic Resonance) Stack of images from MRI (1 mm) Contour extraction by segmentation (using BSplines) Sample points on extracted geometry

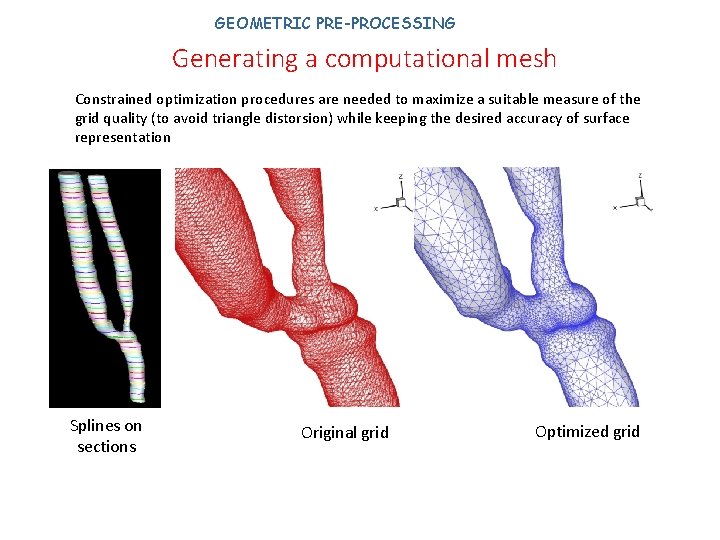
GEOMETRIC PRE-PROCESSING Generating a computational mesh Constrained optimization procedures are needed to maximize a suitable measure of the grid quality (to avoid triangle distorsion) while keeping the desired accuracy of surface representation Splines on sections Original grid Optimized grid

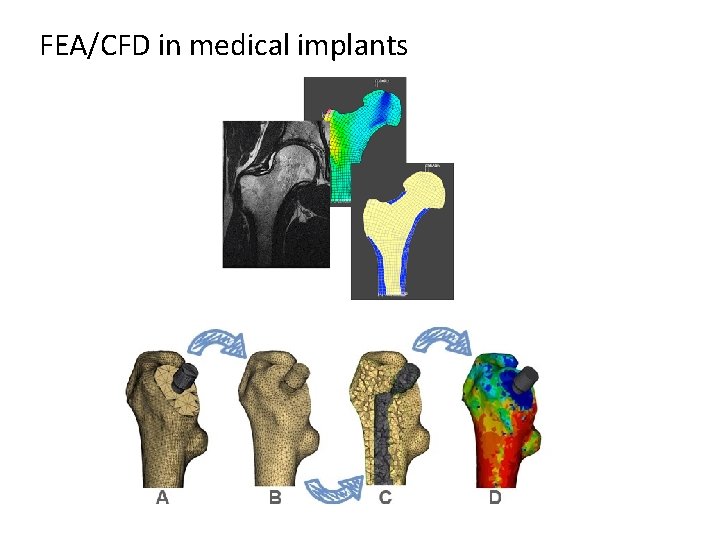
FEA/CFD in medical implants

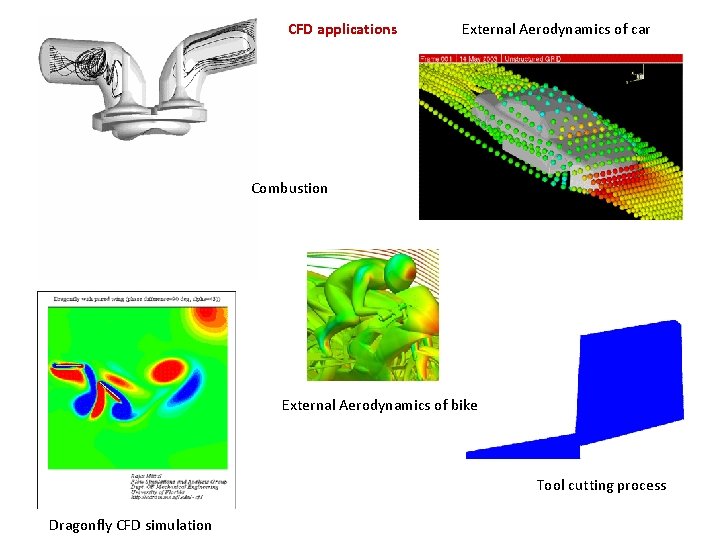
CFD applications External Aerodynamics of car Combustion External Aerodynamics of bike Tool cutting process Dragonfly CFD simulation

End