Introduction Lesson What the Flip Quiz Introduction Intended

Introduction Intended 10 th for: Grade Math Class Learning Upon Objectives: completion students will

Tips Before you flip out, here are some useful tips: To navigate through this

Lesson To better understand the material about to be presented we should touch on

Lesson Reflections A transformation in which a geometric figure is reflected across a line,

Lesson Here’s how to do it: 1. Measure from the point to the LOR

Lesson Labeling It is important to label the corners to show which is the

Lesson Some Rules X-Axis If the line of reflection is the x-axis, just change

Lesson Rotations! A transformation in which a plane figure turns around a fixed center

Lesson Examples Rotation by 90° about the origin (i. e. the center) The general

Lesson Rotation by 180° about the origin The general rule for a 180° rotation

Lesson Rotation by 270° about the origin The general rule for a 270° rotation

Lesson Useful Information A positive number usually means that you will rotate the figure

Lesson Translations! A transformation in which a graph or geometric figure is picked up

Lesson Translations should not alter the size or position of figure All points should

Lesson This figure translated 4 units down and 6 units to the right Can

Lesson It is important to note that all 3 of these symmetries can take

Quiz If you have a grasp on the lesson then it is now time

Quiz Question 1 The original image has a point at (-4, 3), what would

Quiz Correct! From the lesson we learned that if a figure is reflected across

Quiz Question 2 Describe A. B. C. D. this translation: 9 units down, 2

Quiz Correct! The image was translated 6 units down and 3 units to the

Quiz Question 3 A negative number (in degrees) means that the figure will rotate

Quiz Correct! The figure will be rotated CLOCKWISE if it is being rotated by

Quiz Question 4 Translations the figure. A. True B. False will alter the size

Quiz Correct! This statement is false because translations DO NOT alter the size or

Quiz Question 5 The A. B. C. D. general rule for a __° rotation

Quiz Correct! The answer is 180°! Finish

Done CONGRATULATIONS! You have successfully completed the lesson and quiz! I hope you can

Thanks To: http: //www. ode. state. oh. us/GD/Templates/Pages/O DE/ODEDetail. aspx? page=3&Topic. Relation. ID=170 4&Content.

Slides: 43

Download presentation

Introduction Lesson What the Flip! Quiz

Introduction Intended 10 th for: Grade Math Class Learning Upon Objectives: completion students will be able to: Identify the reflection, roation, and translation symmetries of figures Perform Derive reflections, rotations, and translations coordinate rules for reflections, rotations, and translations of geometric figures in the coordinate plane.

Tips Before you flip out, here are some useful tips: To navigate through this Power. Point successfully do the following: To return to the homepage at any given time click the For the lesson, click the if you want to go back to the previous slide or click the button to keep moving forward. To take the quiz, either return to homepage and click quiz, or at the end of the lesson click the which will then take you directly to the quiz. If you need to go back to the lesson at any time during the quiz, just go to the homepage and click lesson and repeat! YOU ARE NOW READY TO BEGIN THE LESSON!

Lesson To better understand the material about to be presented we should touch on what symmetry is. Symmetry- when one shape becomes exactly like another if you flip, slide or turn it. There are 3 different types: 1. 2. 3. Reflection Rotation Translation We will now begin to understand these 3 types of symmetries! Begin Lesson

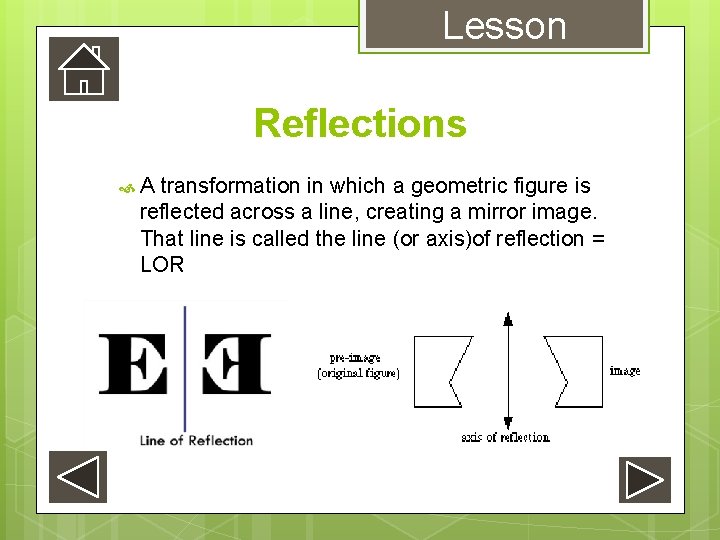
Lesson Reflections A transformation in which a geometric figure is reflected across a line, creating a mirror image. That line is called the line (or axis)of reflection = LOR

Lesson Here’s how to do it: 1. Measure from the point to the LOR Do this for each point on the graph! 2. Measure the same distance again on the other side and place a dot. 3. Connect the new dots and then you have the reflection!

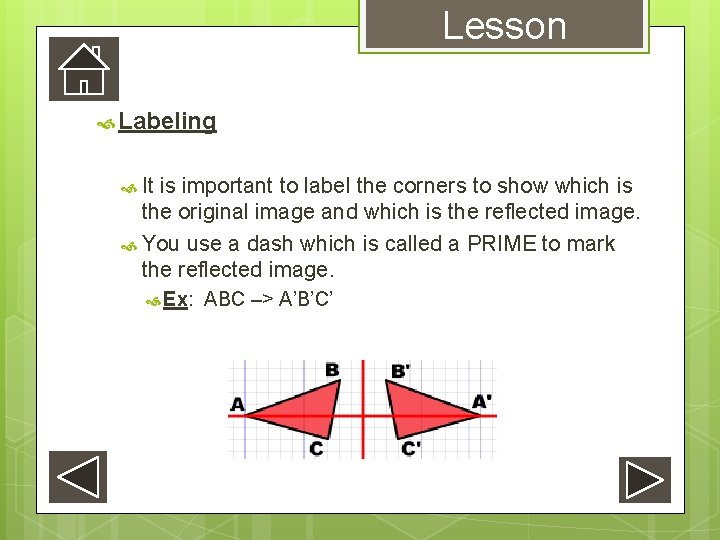
Lesson Labeling It is important to label the corners to show which is the original image and which is the reflected image. You use a dash which is called a PRIME to mark the reflected image. Ex: ABC –> A’B’C’

Lesson Some Rules X-Axis If the line of reflection is the x-axis, just change each (X, Y) into (X, -Y) Y-Axis If the line of reflection is the y-axis, just change each (X, Y) into (-X, Y)

Lesson Rotations! A transformation in which a plane figure turns around a fixed center point. In other words, one point on the plane, the center of rotation, is fixed and everything else on the plane rotates about that point by a given angle.

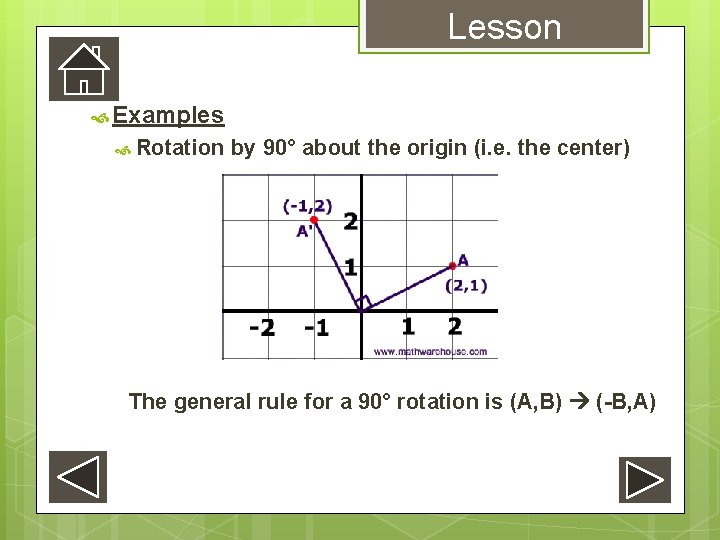
Lesson Examples Rotation by 90° about the origin (i. e. the center) The general rule for a 90° rotation is (A, B) (-B, A)

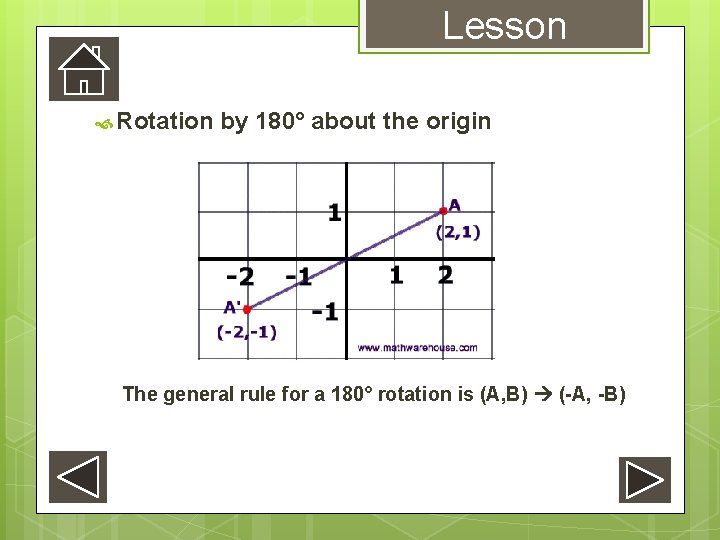
Lesson Rotation by 180° about the origin The general rule for a 180° rotation is (A, B) (-A, -B)

Lesson Rotation by 270° about the origin The general rule for a 270° rotation is (A, B) (B, -A)

Lesson Useful Information A positive number usually means that you will rotate the figure counter clockwise about the center point A negative number then, will mean that you are to rotate the figure clockwise about the center point

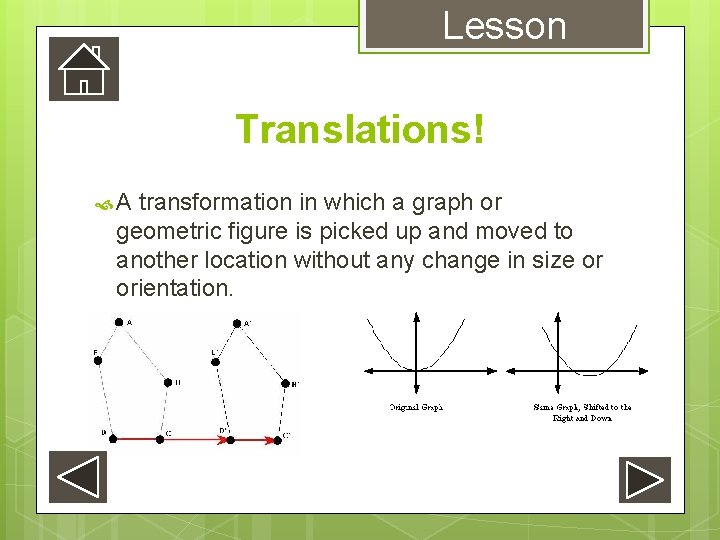
Lesson Translations! A transformation in which a graph or geometric figure is picked up and moved to another location without any change in size or orientation.

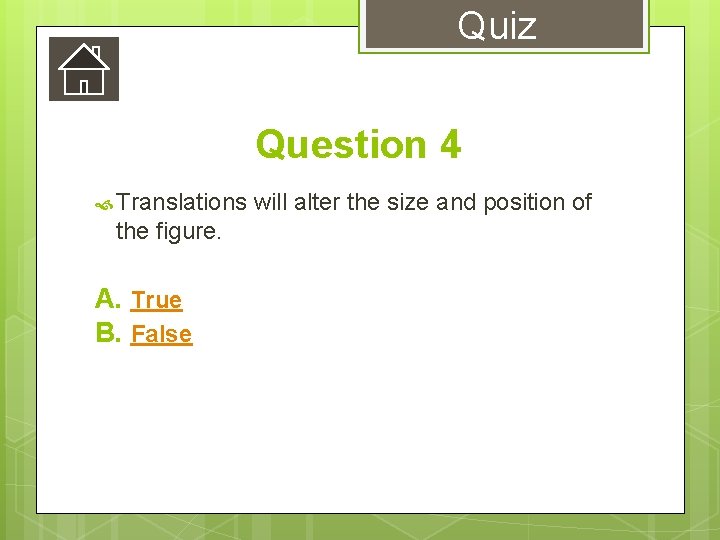
Lesson Translations should not alter the size or position of figure All points should move same direction and distance

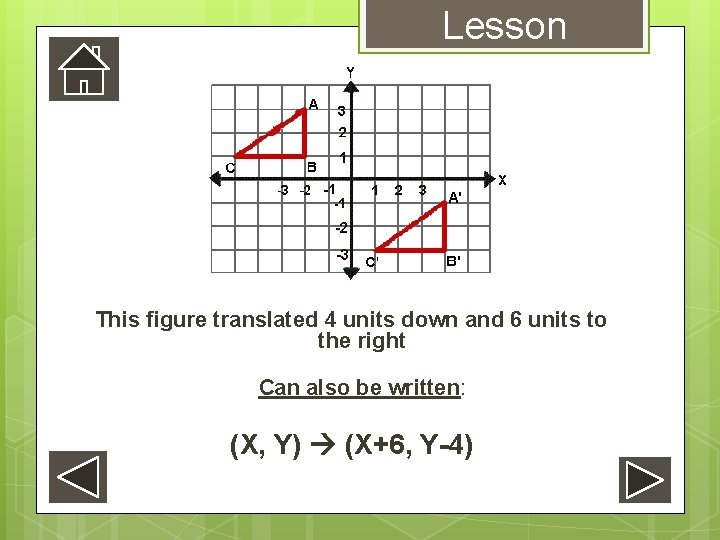
Lesson This figure translated 4 units down and 6 units to the right Can also be written: (X, Y) (X+6, Y-4)

Lesson It is important to note that all 3 of these symmetries can take place in one graph and figure at a time! Once you know them individually it is easy to spot them together as well! You have completed the lesson! Click the star to continue onto the quiz or the moon to go back to the beginning of the lesson!

Quiz If you have a grasp on the lesson then it is now time for you to take the quiz! GOOD LUCK! START

Quiz Question 1 The original image has a point at (-4, 3), what would be it’s reflection point over the x-axis? A. B. C. D. (-4, 0) (-4, -3) (4, 0) (4, 3)

Quiz Correct! From the lesson we learned that if a figure is reflected across the x-axis, you just change each (X, Y) into (X, -Y) So if the original was (-4, 3) then the reflected point would be (-4, -3) Next Question

Quiz Sorry! Try Again!

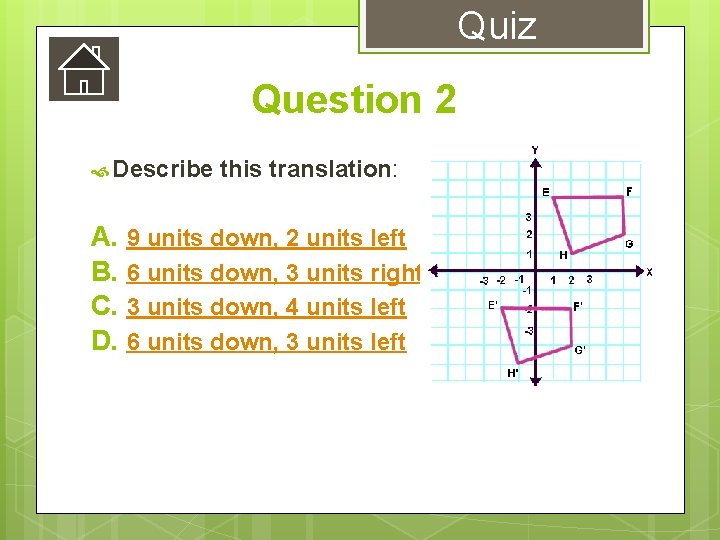
Quiz Question 2 Describe A. B. C. D. this translation: 9 units down, 2 units left 6 units down, 3 units right 3 units down, 4 units left 6 units down, 3 units left

Quiz Correct! The image was translated 6 units down and 3 units to the left! Next Question

Quiz Sorry! Try Again!

Quiz Question 3 A negative number (in degrees) means that the figure will rotate _____? A. B. C. D. Counter Clockwise Horizontally Clockwise Vertically

Quiz Correct! The figure will be rotated CLOCKWISE if it is being rotated by a negative degree! Meaning, it will be rotated counter clockwise if by a positive degree! Next Question

Quiz Sorry! Try Again!

Quiz Question 4 Translations the figure. A. True B. False will alter the size and position of

Quiz Correct! This statement is false because translations DO NOT alter the size or position of the figure! Next Question

Quiz Sorry! Try Again!

Quiz Question 5 The A. B. C. D. general rule for a __° rotation is (A, B) (-A, -B) 180° 90° 0/360° 270°

Quiz Correct! The answer is 180°! Finish

Quiz Sorry! Try Again!

Done CONGRATULATIONS! You have successfully completed the lesson and quiz! I hope you can now confidently perform reflections, rotations, and translations of figures! Go out and show the world how you flip, turn, & slide!

Thanks To: http: //www. ode. state. oh. us/GD/Templates/Pages/O DE/ODEDetail. aspx? page=3&Topic. Relation. ID=170 4&Content. ID=801&Content=112057 http: //www. mathwords. com/s/shift. htm http: //www. mathsisfun. com/index. htm http: //www. mathwarehouse. com/transformations/rot ations-in-math. php http: //regentsprep. org/Regents/math/geometry/GT 2/ Trans. htm