Introduction la logique Introduction aux fonctions logiques v

Introduction à la logique

Introduction aux fonctions logiques v Systèmes binaires ¤ Deux états fondamentaux et distincts Vrai / Faux Marche / Arrêt Oui / Non v Par convention ¤ Un état est représenté par « 1 » ¤ L’autre est représenté par « 0 »

La logique Booléenne v George Boole (1815 -1864), mathématicien et logicien anglais. v Il décrit un système algébrique, l’algèbre booléenne.

Types de représentation v Les fonctions logiques peuvent être représentées de plusieurs façons ¤ Équations logiques ¤ Tables de vérités ¤ Représentation graphique v Ces représentations seront introduites avec les fonctions de base. . .

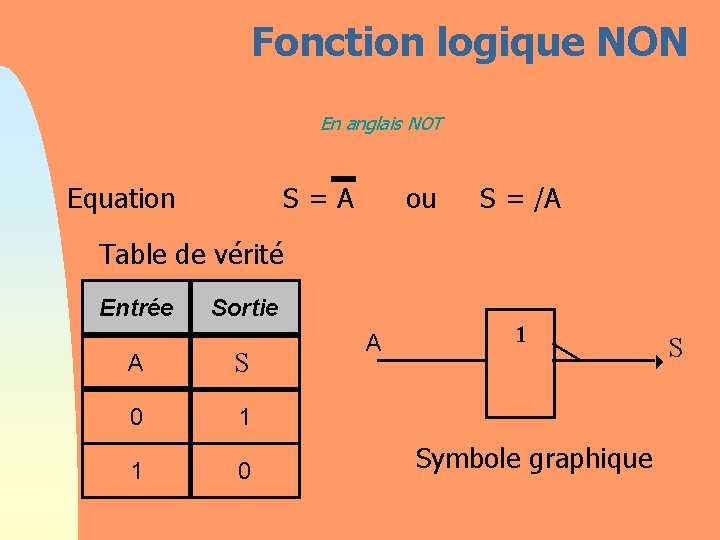
Fonction logique NON En anglais NOT Equation S = A ou S = /A Table de vérité Entrée Sortie A S 0 1 1 0 A 1 Symbole graphique S

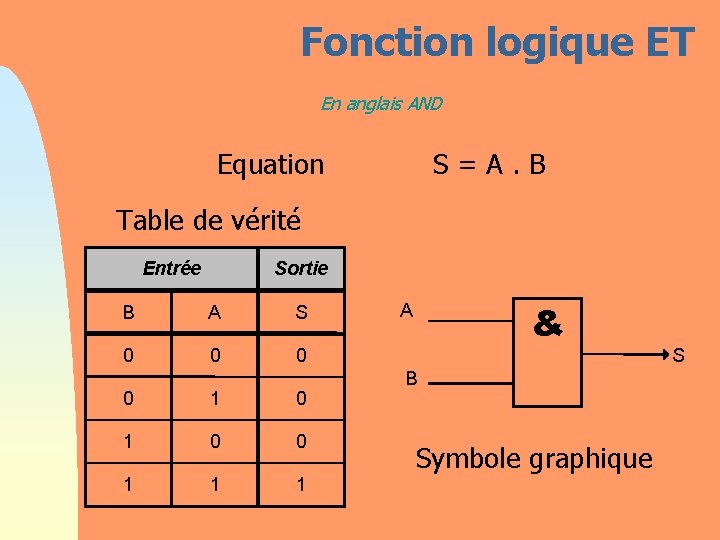
Fonction logique ET En anglais AND Equation S = A. B Table de vérité Entrée Sortie B A S 0 0 1 1 1 & A B Symbole graphique S

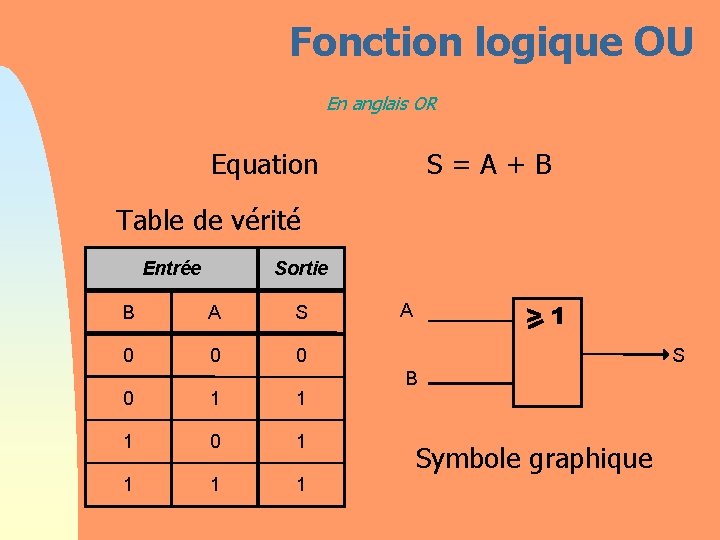
Fonction logique OU En anglais OR Equation S = A + B Table de vérité Entrée Sortie B A S 0 0 1 1 1 0 1 1 >1 A S B Symbole graphique

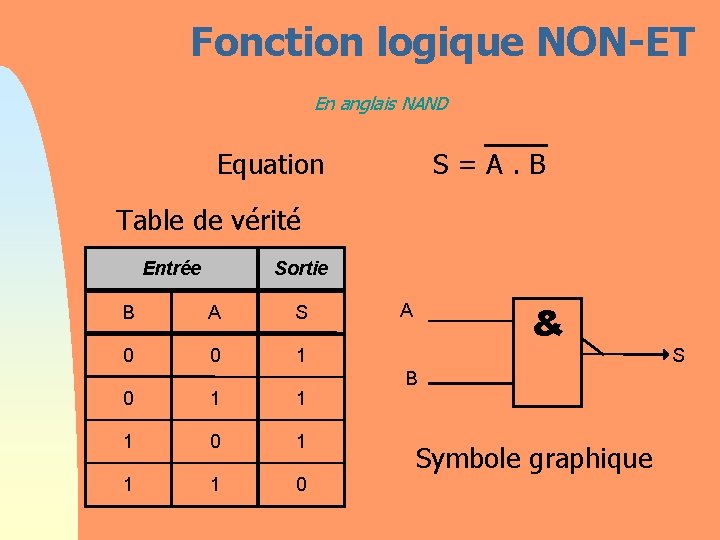
Fonction logique NON-ET En anglais NAND Equation S = A. B Table de vérité Entrée Sortie B A S 0 0 1 1 1 0 & A B Symbole graphique S

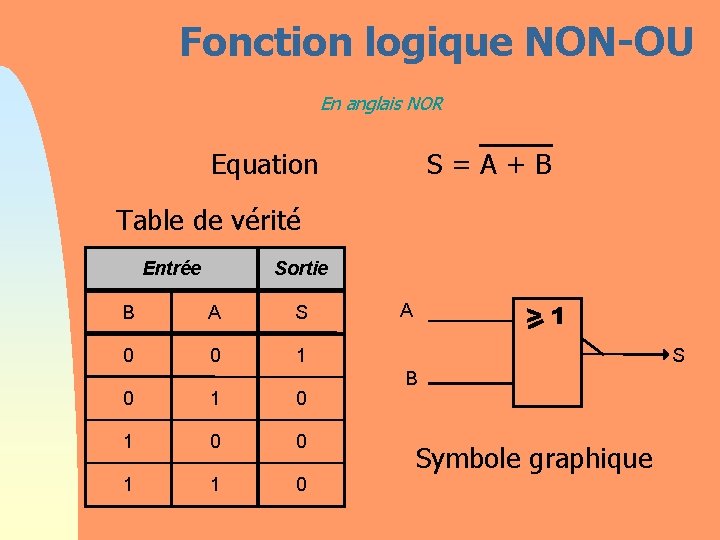
Fonction logique NON-OU En anglais NOR Equation S = A + B Table de vérité Entrée Sortie B A S 0 0 1 0 1 0 0 1 1 0 >1 A S B Symbole graphique

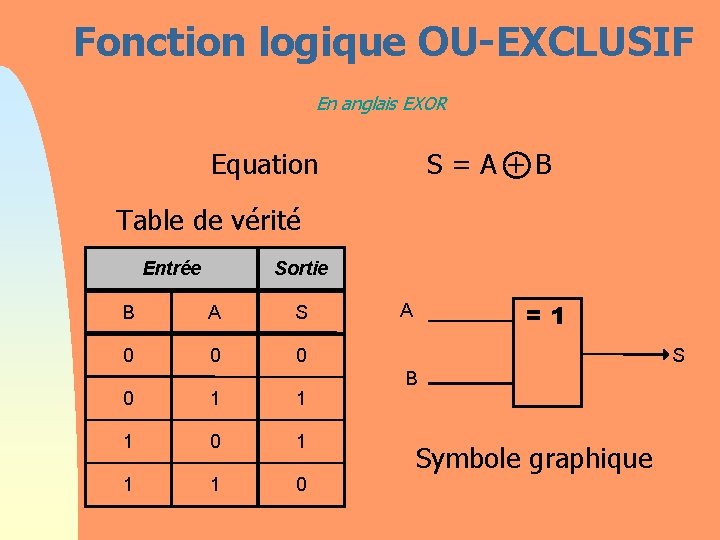
Fonction logique OU-EXCLUSIF En anglais EXOR Equation S = A + B Table de vérité Entrée Sortie B A S 0 0 1 1 1 0 =1 A S B Symbole graphique

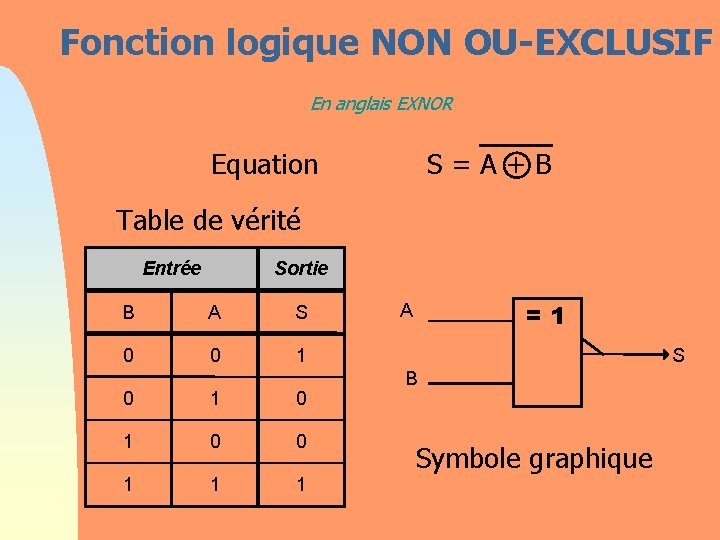
Fonction logique NON OU-EXCLUSIF En anglais EXNOR Equation S = A + B Table de vérité Entrée Sortie B A S 0 0 1 0 1 0 0 1 1 1 =1 A S B Symbole graphique

Technologie différentes v En électronique, on représente les fonctions logiques avec des logigrammes. v En automatisme, on utilise des interrupteurs et des relais pour représenter les fonctions logiques.

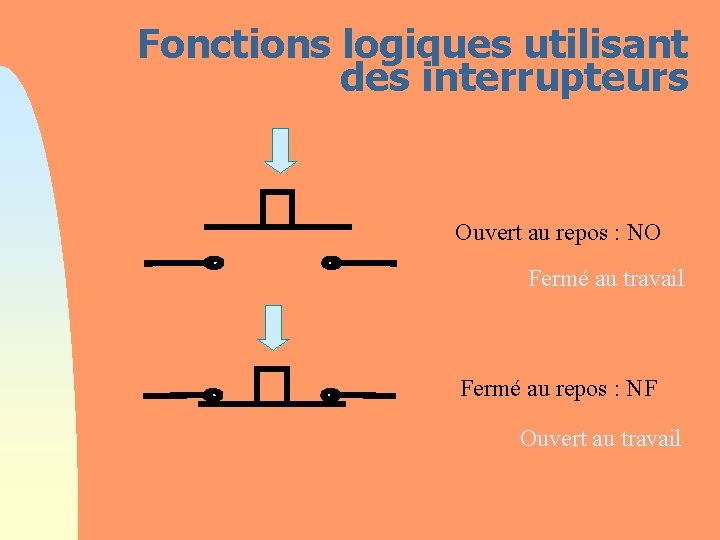
Fonctions logiques utilisant des interrupteurs Ouvert au repos : NO Fermé au travail Fermé au repos : NF Ouvert au travail

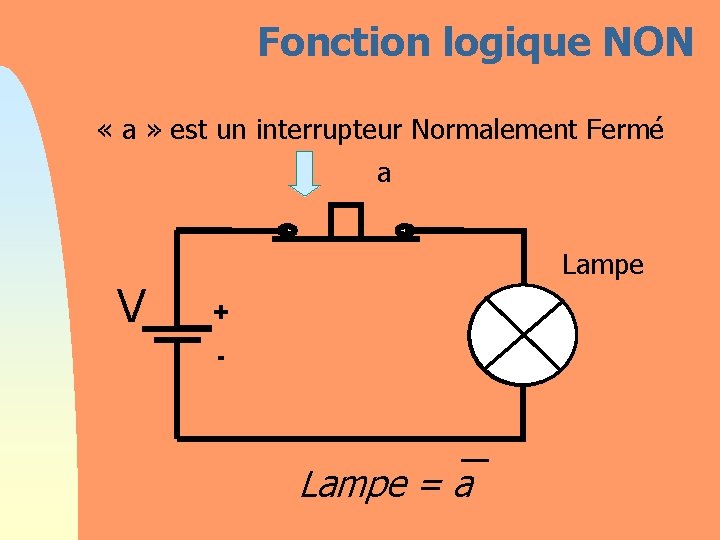
Fonction logique NON « a » est un interrupteur Normalement Fermé a Lampe V + - Lampe = a

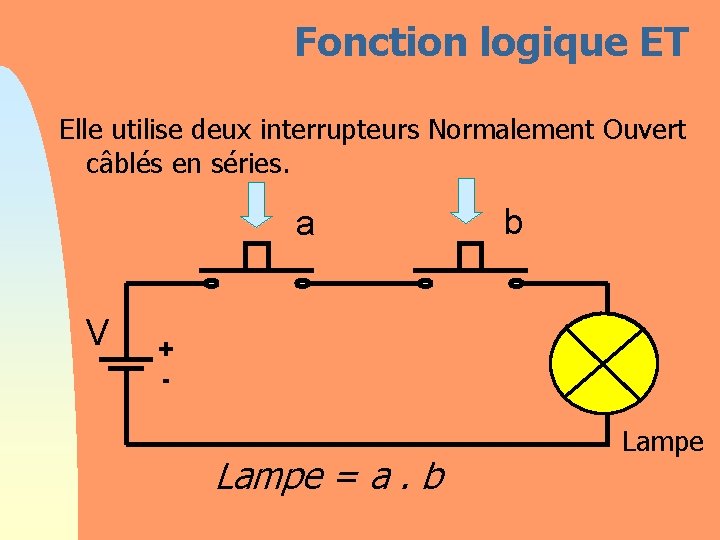
Fonction logique ET Elle utilise deux interrupteurs Normalement Ouvert câblés en séries. a V b + - Lampe = a. b Lampe

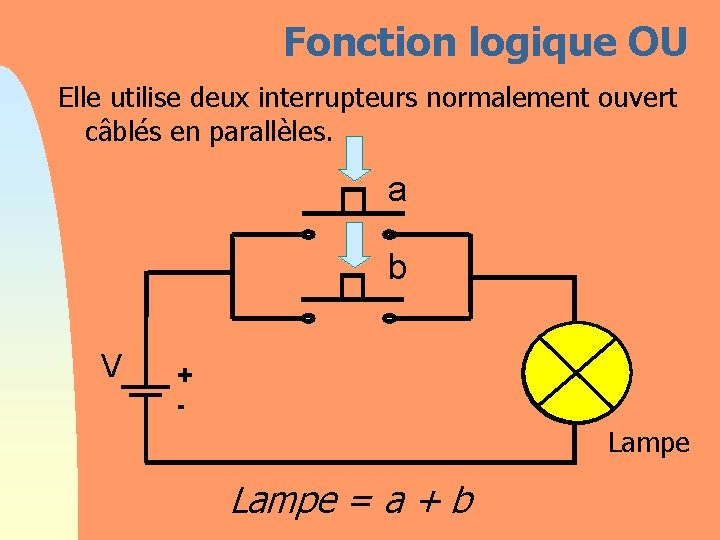
Fonction logique OU Elle utilise deux interrupteurs normalement ouvert câblés en parallèles. a b V + - Lampe = a + b

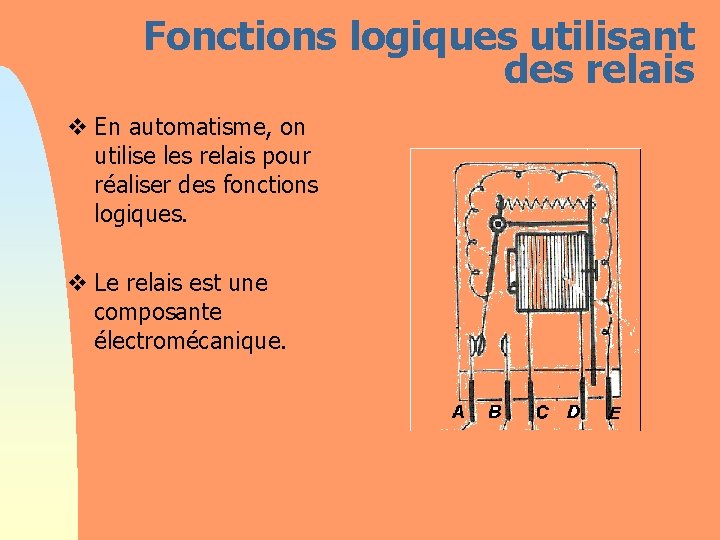
Fonctions logiques utilisant des relais v En automatisme, on utilise les relais pour réaliser des fonctions logiques. v Le relais est une composante électromécanique.

L’algèbre Booléenne v Commutativité ¤ A + B = B + A ¤ A. B = B. A v Associativité ¤ A + (B + C) = (A + B) + C ¤ A. (B. C) = (A. B). C

L’algèbre Booléenne v Distributivité ¤ Du ET par rapport au OU : A. (B + C) = (A. B) + (A. C) ¤ Du OU par rapport ET : A + (B. C) = (A + B). (A + C)

L’algèbre Booléenne v Idempotence ¤ A + A = A ¤ A. A = A v Complémentarité ¤ A + A = 1 ¤ A. A = 0

L’algèbre Booléenne v Identités remarquables ¤ 1 + A = 1 1. A = A ¤ 0 + A = A 0. A = 0 v Théorème de de Morgan ¤ a. b = a + b ¤ a + b = a. b Application principale : Transformation d’un ET en OU et inversement

Applications v A partir d’une table de vérité, nous pouvons trouver l’équation logique et le logigramme correspondant. v L’algèbre de Boole est utilisée pour simplifier les équations.

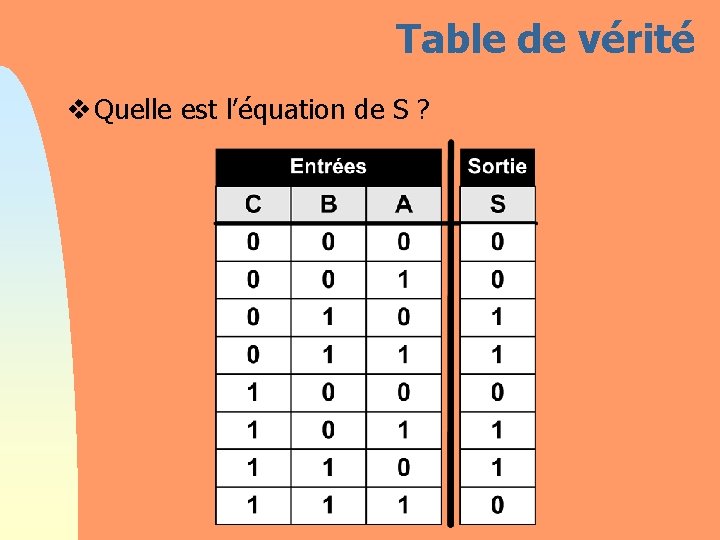
Table de vérité v Quelle est l’équation de S ?

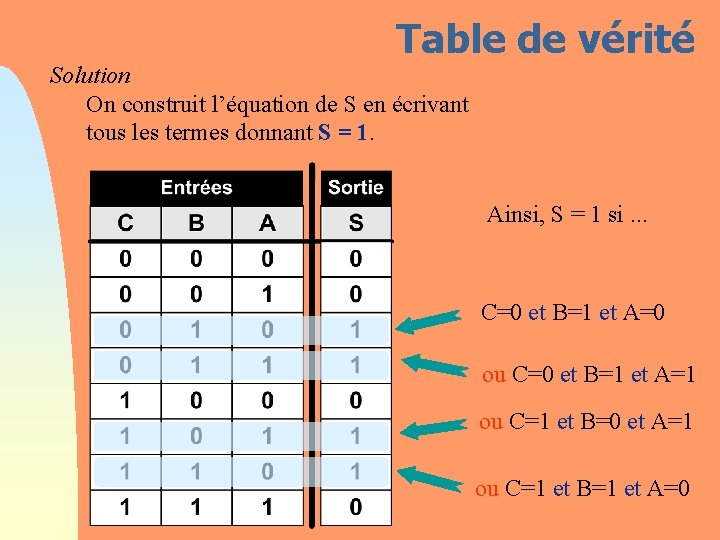
Table de vérité Solution On construit l’équation de S en écrivant tous les termes donnant S = 1. Ainsi, S = 1 si. . . C=0 et B=1 et A=0 ou C=0 et B=1 et A=1 ou C=1 et B=0 et A=1 ou C=1 et B=1 et A=0

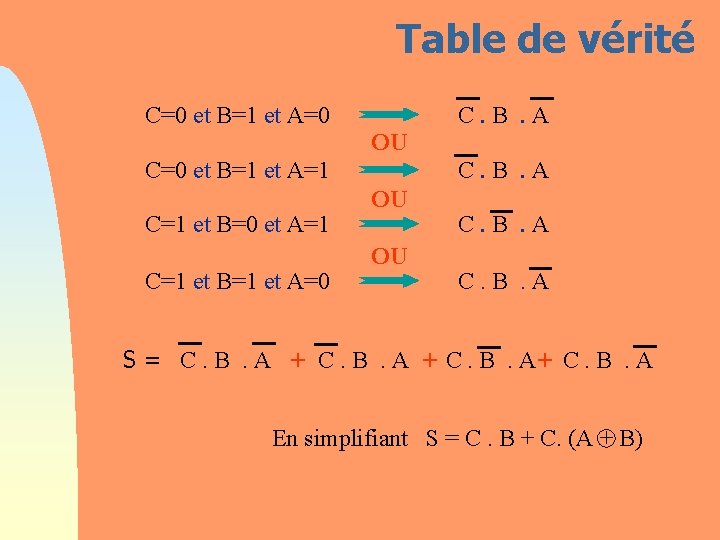
Table de vérité C=0 et B=1 et A=0 C. B. A OU C=0 et B=1 et A=1 C=1 et B=0 et A=1 C=1 et B=1 et A=0 C. B. A OU OU C. B. A C + +. B. A C. B. A S = + En simplifiant S = C. B + C. (A + B)

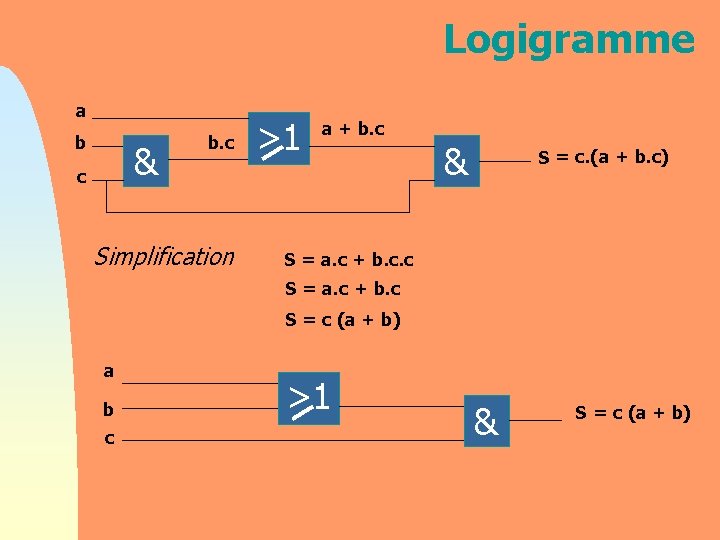
Logigramme a b & c b. c Simplification >1 a + b. c & S = c. (a + b. c) S = a. c + b. c. c S = a. c + b. c S = c (a + b) a b c >1 & S = c (a + b)

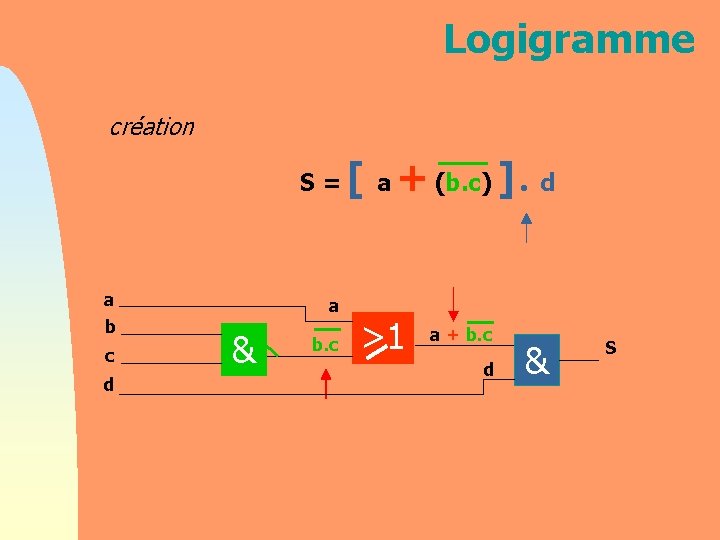
Logigramme création S= a b c d a & b. c [ a + (b. c) ]. d >1 a + b. c d & S

Conclusion v Ces exemples démontre que la simplification est essentielle. Il faut avoir le circuit le plus simple que possible. . . v La simplification peut être un processus long si le système est complexe.