Introduction Integration is the reverse process of Differentiation

Introduction • Integration is the reverse process of Differentiation • Differentiating gives us a formula for the gradient • Integrating can get us the formula for the curve, if we know the gradient function • It can also be used to calculate the Area under a curve

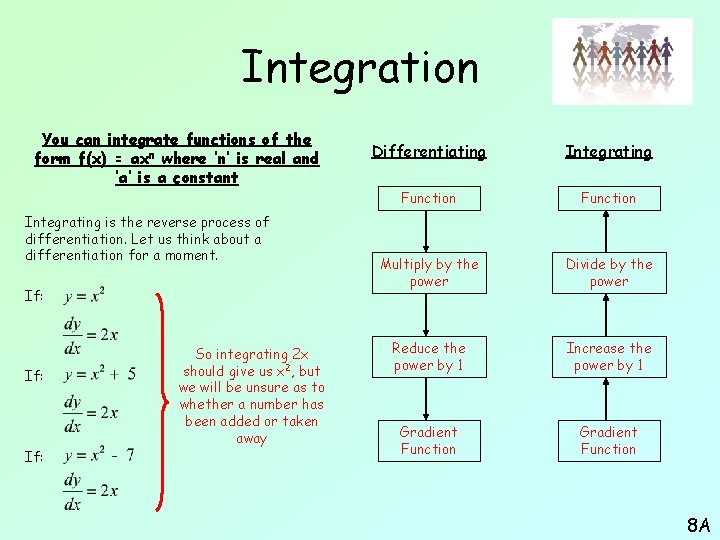
Integration You can integrate functions of the form f(x) = axn where ‘n’ is real and ‘a’ is a constant Integrating is the reverse process of differentiation. Let us think about a differentiation for a moment. If: So integrating 2 x should give us x 2, but we will be unsure as to whether a number has been added or taken away Differentiating Integrating Function Multiply by the power Divide by the power Reduce the power by 1 Increase the power by 1 Gradient Function 8 A

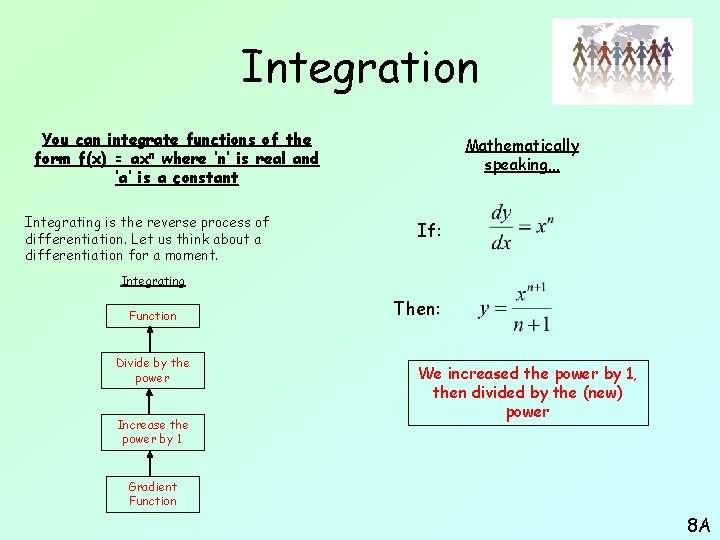
Integration You can integrate functions of the form f(x) = axn where ‘n’ is real and ‘a’ is a constant Integrating is the reverse process of differentiation. Let us think about a differentiation for a moment. Mathematically speaking… If: Integrating Function Divide by the power Increase the power by 1 Then: We increased the power by 1, then divided by the (new) power Gradient Function 8 A

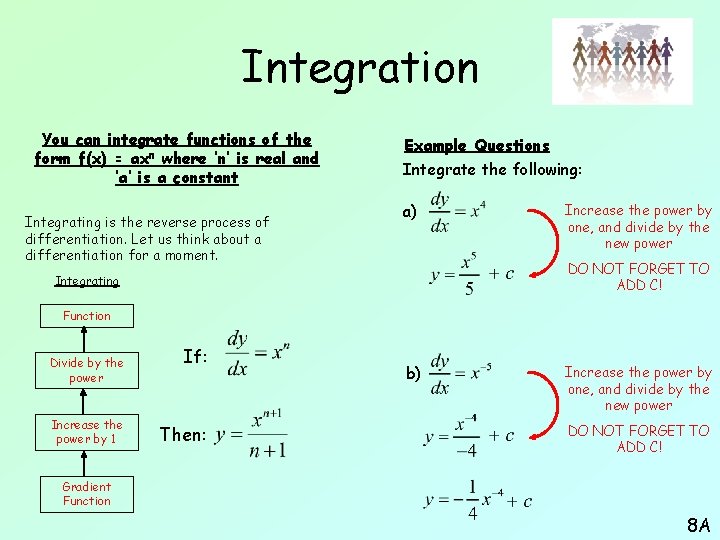
Integration You can integrate functions of the form f(x) = axn where ‘n’ is real and ‘a’ is a constant Integrating is the reverse process of differentiation. Let us think about a differentiation for a moment. Example Questions Integrate the following: a) Increase the power by one, and divide by the new power DO NOT FORGET TO ADD C! Integrating Function Divide by the power Increase the power by 1 If: Then: b) Increase the power by one, and divide by the new power DO NOT FORGET TO ADD C! Gradient Function 8 A

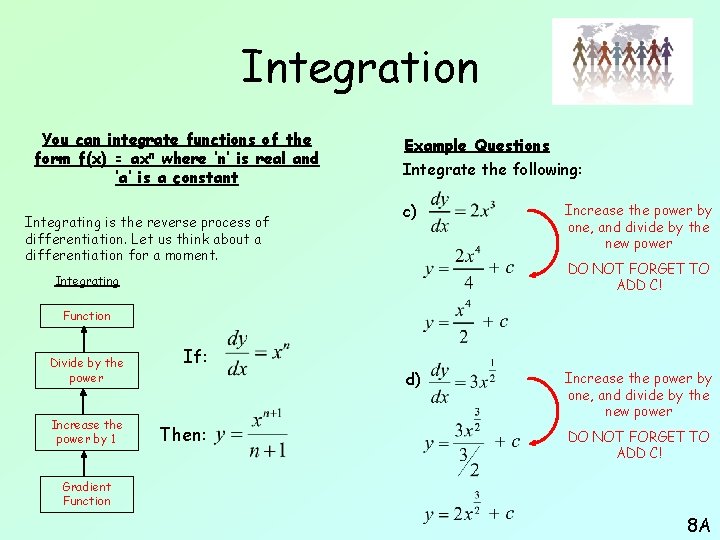
Integration You can integrate functions of the form f(x) = axn where ‘n’ is real and ‘a’ is a constant Integrating is the reverse process of differentiation. Let us think about a differentiation for a moment. Example Questions Integrate the following: c) Increase the power by one, and divide by the new power DO NOT FORGET TO ADD C! Integrating Function Divide by the power Increase the power by 1 If: Then: d) Increase the power by one, and divide by the new power DO NOT FORGET TO ADD C! Gradient Function 8 A

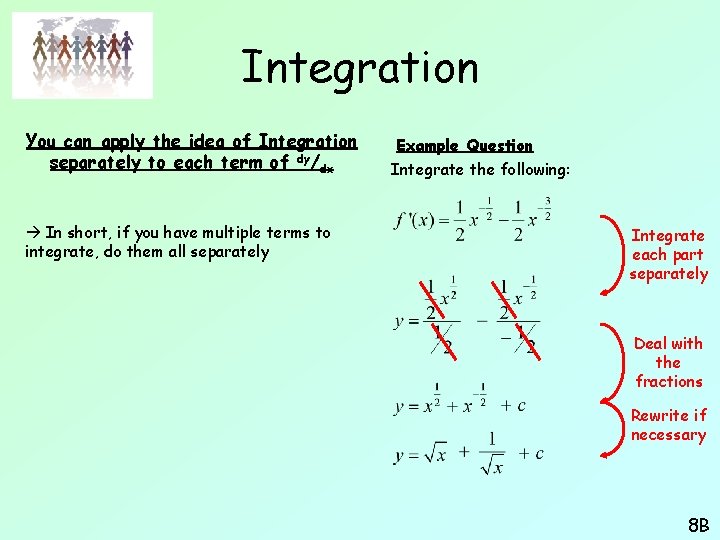
Integration You can apply the idea of Integration separately to each term of dy/dx In short, if you have multiple terms to integrate, do them all separately Example Question Integrate the following: Integrate each part separately ‘Tidy up’ terms if possible 8 B

Integration You can apply the idea of Integration separately to each term of dy/dx In short, if you have multiple terms to integrate, do them all separately Example Question Integrate the following: Integrate each part separately Deal with the fractions Rewrite if necessary 8 B

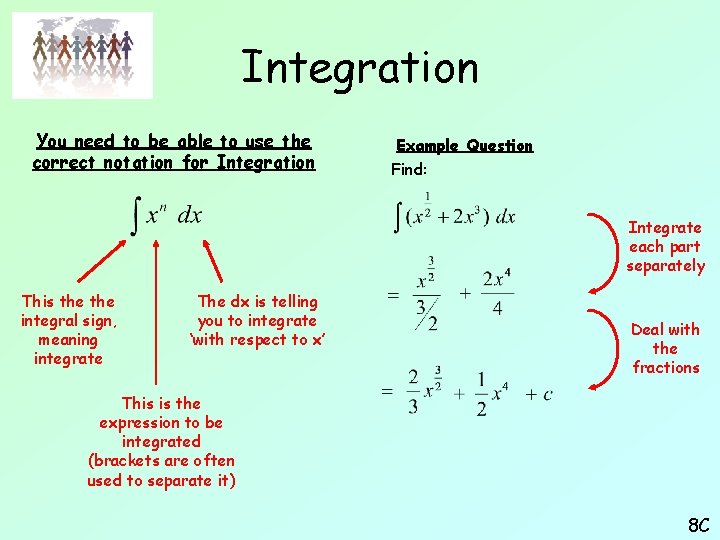
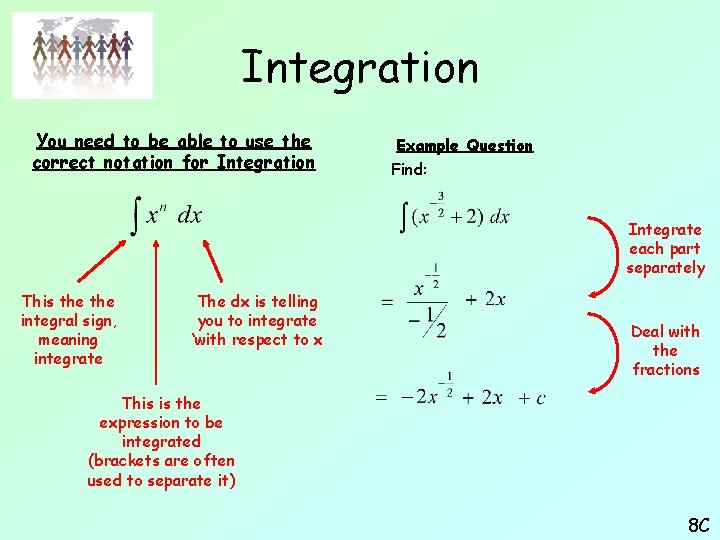
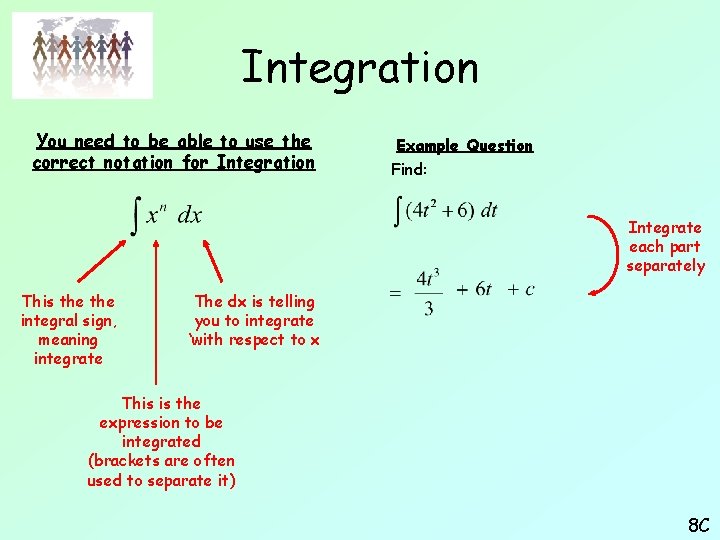
Integration You need to be able to use the correct notation for Integration Example Question Find: Integrate each part separately This the integral sign, meaning integrate The dx is telling you to integrate ‘with respect to x’ Deal with the fractions This is the expression to be integrated (brackets are often used to separate it) 8 C

Integration You need to be able to use the correct notation for Integration Example Question Find: Integrate each part separately This the integral sign, meaning integrate The dx is telling you to integrate ‘with respect to x Deal with the fractions This is the expression to be integrated (brackets are often used to separate it) 8 C

Integration You need to be able to use the correct notation for Integration Example Question Find: Integrate each part separately This the integral sign, meaning integrate The dx is telling you to integrate ‘with respect to x This is the expression to be integrated (brackets are often used to separate it) Deal with the fractions p and q 2 should be treated as if they were just numbers! 8 C

Integration You need to be able to use the correct notation for Integration Example Question Find: Integrate each part separately This the integral sign, meaning integrate The dx is telling you to integrate ‘with respect to x This is the expression to be integrated (brackets are often used to separate it) 8 C

Integration All terms need to be written in then form axn before Integrating (similar to differentiation!) Rewrite terms Integrate the function to the right: Integrate each part Simplify ADD C!!!!! Ensure you integrate each term in the same step! A common mistake is that people integrate one term while rewriting another They then integrate and have therefore integrated a term twice! 8 D

Integration All terms need to be written in then form axn before Integrating (similar to differentiation!) Integrate the function to the right: Rewrite the fraction part, multiply the ‘mini bracket’ Rewrite terms Integrate Simplify and ADD C!!!!! Ensure you integrate each term in the same step! A common mistake is that people integrate one term while rewriting another They then integrate and have therefore integrated a term twice! 8 D

Integration You can find the constant of integration, c, if you are given a point that the function passes through Example Question The curve X with equation y = f(x) passes through the point (2, 15). Given that: Find the equation of X. Up until now we have written ‘c’ when Integrating. Integrate The point of this was that if we differentiate a number on its own, it disappears. Sub in (2, 15) Consequently, when integrating, we cannot be sure whether a number was there originally, and what it was if there was one… Work out each fraction Step 1: Integrate as before, putting in ‘c’ Step 2: Substitute the coordinate in, and work out what ‘c’ must be to make the equation balance. . Add the fractions together Work out c 8 E

Integration You can find the constant of integration, c, if you are given a point that the function passes through Up until now we have written ‘c’ when Integrating. The point of this was that if we differentiate a number on its own, it disappears. Consequently, when integrating, we cannot be sure whether a number was there originally, and what it was if there was one… Step 1: Integrate as before, putting in ‘c’ Step 2: Substitute the coordinate in, and work out what ‘c’ must be to make the equation balance. . Example Question The curve X with equation y = f(x) passes through the point (4, 5). Given that: Find the equation of X. Split into 2 parts Write in the form axn Integrate 8 E

Integration You can find the constant of integration, c, if you are given a point that the function passes through Up until now we have written ‘c’ when Integrating. The point of this was that if we differentiate a number on its own, it disappears. Consequently, when integrating, we cannot be sure whether a number was there originally, and what it was if there was one… Step 1: Integrate as before, putting in ‘c’ Step 2: Substitute the coordinate in, and work out what ‘c’ must be to make the equation balance. . Example Question The curve X with equation y = f(x) passes through the point (4, 5). Given that: Find the equation of X. Rewrite for substitution y = 5, x = 4 Work out each part carefully 8 E

Summary • We have learnt what Integration is • We have seen it combined with rewriting for substitution • We have learnt how to calculate the missing value ‘c’, and why it exists in the first place