Introduction Distributed object matching Requirements Recognition Methods Experiments

Introduction Distributed object matching Requirements Recognition Methods Experiments and Results Conclusion Proposed question

Feature is a function that maps an image into a real number or a vector (array of real numbers) A node in a Visual Sensor Network(VSN) is an object Primary task of this node : is acquisition of images via its visual sensor processing of those images according to a particular task Object Matching: Given the newly acquired object features at one of the nodes, find whether any of the (distant) nodes in the network has seen same/similar object before Thus it is about the knowledge distribution (feature distribution) in visual-sensor networks

Distributed object matching: Given the acquired image of an object, find all the images of visually similar objects that have been acquired by any of the nodes on any previous occasion Object matching consists of the following two phases: Learning phase: compact representation (model) of the object is extracted from one or more images and stored Matching phase: Same compact representation of an object is extracted from the newly acquired image Entire network can be flooded with image data or object features whenever a new image is acquired every image would be distributed to each node, which constitutes an extremely wasteful use network resources To avoids the distribution of complete feature vectors “hierarchical encoding scheme

Based on Hierarchical reduction of feature vectors: Require that the primary node retains the complete information about the object Its neighbours receive-> less detailed, more abstract information which generally requires less storage and transmission capacity Amount of data transmitted across, or stored in the network, can be significantly reduced

Features are distributed by flooding, each node (b) Hierarchical distribution scheme is used, receives an exact copy of the original feature vector the nodes receive progressively less-detailed (more abstract) feature vectors (shades of (black) grey (a)

Structure leads to a loss of information->when the features are transformed to their less detailed representations In general->leads to a decrease In the matching performance To reduce the amount of traffic, while preserving matching performance four requirement that have to be fulfilled by any recognition method, to ensure that results of recognition or Object matching in a distributed architecture will be the same as in non-distributed architecture to be considered for use in the proposed hierarchical scheme

Requirment 1(Abstraction) , 0< n ≤ N, (N highest level of abstraction) Translates a level n feature vector x(n) into a more higher abstract level (n + 1) feature vector x(n+1) with reduced dimensionality Requirment 2: S(x) is the storage space required for the feature vector x in bits, then it should hold that: If this requirement is not fulfilled the hierarchical encoding scheme does not provide an improvements Ex: network traffic and data storage

Requirement 3 (Existence of a metric) There exists a metric which provides a measure of the similarity between two feature vectors x (n)1 and x (n)2 of the same level n Requirement 4 Two vectors x(n)1 and x(n)2 that are similar, d(n)(x(n)1 , x(n)2 ) ≤ T, the corresponding vectors on the next level n + 1 should be at least as similar as the vectors on the previous level, which converges, meaning that the measure at level N+1 is not larger than the measure at level N. Main idea is that if there is no match at higher level N+1 then there is no match at lower level N

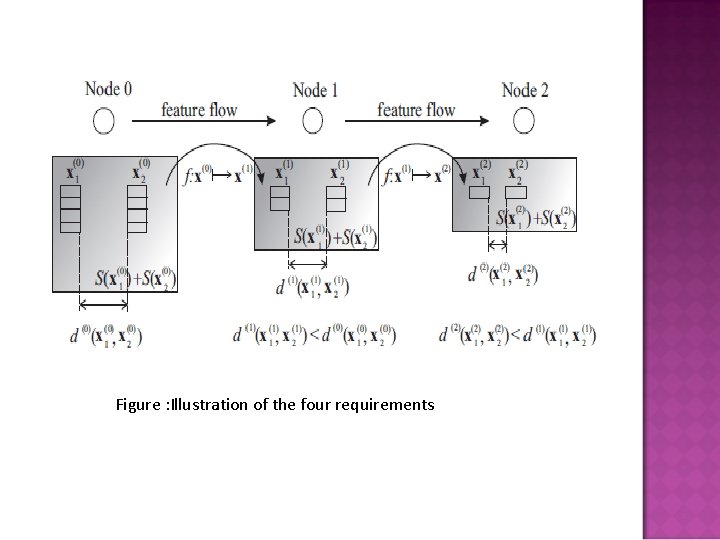
Figure : Illustration of the four requirements

Authors shows how one object can map four basic pattern (object) recognition methods onto the distributed visual sensor network using hierarchical feature-distribution scheme Principal component analysis Haar transform Template matching Histogram 1)Principal component analysis and 2 D Haar transform: PCA is a vector-space transform reduces multidimensional data sets to lower dimensions, while minimizing the loss of information. 2)Haar transform linear transformation into the subspace of Haar function (Haar wavelets). In our case, 2 D Haar transform was used and the feature vectors were obtained by unwrapping the transformation result into a column

o Mapping and the metric which four methods fulfill stated requirements Requirement 1: PCA: Constructed feature vectors contain feature values that are already ordered by decreasing importance in terms of the reconstruction of the original data. This opens up the possibility of the mapping function f : x(n) → x(n+1), which can be defined as dropping a certain number of features with the lowest importance from the feature vector The same mapping was also used for the Haar feature vectors

Requirement 2: It is fulfilled, since dropping any number of dimensions from the feature vector decreases the required storage space Requirement 3: Considering the metric d(n)(x(n)1 , x(n)2 ), the Euclidean distance is used when comparing PCA-based or Haar-based feature vectors Requirement 4: It is easy to show that Requirement 4 holds as well, if the Euclidean distance is used. Ignoring one of the dimensions from the Euclidean space(or even any inner product space) never increases the distance between the two points. At most, the distance remains the same. This also holds for high-dimensional cases. That means, regardless of the order of the features, the distance will always decrease with the decreased dimensionality of the feature vectors, and Requirement 4 is fulfilled.

Requirement 3: metric d(n)(x(n)1 , x(n)2 )as the Euclidean distance between the feature vectors. Requirement 4: Let us use metric d(n) to compare two images A(n) and B(n) have the dimensions k × k and the resized images A(n+1) and B(n+1) have the dimensions k/2 × k/2. Let x(n)A , x(n)B , x(n+1)A , x(n+1)B be the level n and (n + 1) feature vectors, respectively. Since the following inequality holds: Requirement 4 is fulfilled

4)Histogram: Let I be an image. Intensity histogram with P bins sampled within the image I, is defined as: where u = (x, y) denotes a pixel within the image region is the Kronecker delta function positioned at histogram bin i and p(u) ∈ {1. . . P} denotes the histogram bin index associated with the intensity of a pixel at location u and fh is a normalizing constant such taht

Requirement 1: mapping f : x(n) →x(n+1) as an operation that combines adjoining bins. Requirement 2: Since a smaller number of bins requires less storage space, Requirement 2 is fulfilled. Requirement 3: metric d(n)(x(n)1 , x(n)2 ) can be the distance between the histograms distance between the feature vector Bhattacharyya coefficient Note that there are other possible choices for the metric d, e. g. , Histogram-intersection-based distance[4]

Requirment 4: Let us assume two images A(n) and B(n) with the corresponding histograms h(n)A , h(n)B. Let x(n)A , x(n)B and h(n) A , h(n) B be the level n feature vectors level n histograms x(n+1)A , x(n+1)B and h(n+1)A , h(n+1)B be the feature vectors and the level n + 1 histograms, following inequality holds:

Janez, Matej Kristan selected publicly available COIL-100 (Columbia Object Image Library COIL 100) image database to test the proposed hierarchical feature-distribution scheme[3] It contains the images of 100 different objects, each one rotated by 5 degrees, 72 images per object. Simulation was performed on rectangular 4 -connected grid networks Three feature distribution methods were simulated. Flooding at match Flooding−at−learn M-hier

Flooding at Match : “Flooding means that each node receives a copy of the feature vector” Captured visual information is stored locally and each task of finding an object has to be broadcasted across the network by flooding, for each new image acquired. Such a method of distribution requires little or no network traffic during the learning phase; however, it produces a large amount of data transmitted in the matching phase Flooding-at-learn: Captured visual information from each sensor is distributed to all the nodes for local storage. Again, flooding is used for this purpose. Detection(find out) of similar objects is then performed locally by each sensor as new images are acquired In contrast to the first method, large amount of data transmitted during the learning phase and requires very little or no traffic during the matching phase

M-hier (Hierarchical distribution scheme) original feature vectors are flooded as follows. Detecting node is the only one with the highest level 1 feature vector Its horizontal and vertical neighbors receive level 2 feature vectors from it These neighbors in turn forward level 2 feature vectors to its horizontal and vertical neighbors in an expanding direction. This process continues until reaching the highest defined level H Afterwards flooding will continue by expanding further level H feature to the remaining nodes in the network

During flooding, the coordinates of source node can also be propagated in addition to feature vector(OBEJCET). When a new copy of object is detected, it is compared with locally available feature vectors, at the level that feature is available there. For those that match, the highest level 1 feature of tested object are sent to original source by backward links (can be done horizontally then vertically). The source node then can decide if there is a match Comparison includes the communication load on the network. It can be simplified by counting each transmitted feature vector of length L as load

Main remarks is that proposed algorithm M-hier is not sufficiently scalable It is still based on flooding the whole network, Alternative is quorum based system which consumes bandwidth despite reducing level information. where features are distributed across a row, but search is made across a column The direct Improvement of M-hier is then Q-hier.

Q-Hier: Feature vectors of detected object are distributed in its column only, in the same way, instead of whole network. Search is then performed in the row, by transmitting the lowest level 1 feature vector At intersecting row and column called as “rendezvous”, matching can be made at level available there. If no match, search stops. In case of match, lowest level 1 feature is forwarded toward original source.

D S

Flooding is avoided in the whole network. Note that if we have only one level of feature vectors (H=1) then Q-hier is simply a quorum based scheme. Since we will simulate only rectangular networks, it is then the basic row-column variant of it.

To achieve matching performance as with the full distribution of feature vectors authors propose a set of requirements regarding abstraction, storage space, similarity metric and convergence. Requirements has to be fulfilled by the object-matching method in order for it to be used To show the performance of feature distributed method schema, which aims to reduce the amount of traffic transmitted, while still preserving the matching performance, four object-matching methods were selected. For these methods proved that they satisfy the four requirements of feature-distribution method. The proposed distribution was compared with two flood-feature distributions using our network simulator. The proposed hierarchical feature distribution outperformed both floodbased feature distributions, without any degradation in the matching performance Improvement of M-hier is the Q-hier

Sulic, V. ; Pers, J. ; Kristan, M. ; Kovacic, S. ; Fac. of Electr. Eng. , Univ. of Ljubljana, Slovenia. Efficient Feature Distribution for Object Matching in Visual-Sensor Networks, Volume: 21 issue 7 page(s): 903 – 916, july 2011 Dandan Liu; Ivan Stojmenovic; Xiaohua Jia; Comput. Sch. , Wuhan Univ. A Scalable Quorum Based Location Service in Ad Hoc and Sensor Networks. 2006 S. A. Nene, S. K. Nayar, and H. Murase, “Columbia object image library(coil-100), ” Department of Computer Science, Columbia University, Tech. Rep. CUCS-006 -96, 1996 M. J. Swain and D. H. Ballard, “Color indexing, ” Int. J. Comput. Vis. , vol. 7, pp. 11– 32, 1991

Question 1: (a) What is object matching ? (b) What are the phase object matching consists? (c) How we would avoid the distribution of complete feature vectors? Ans: (a) Given the newly acquired object features at one of the nodes, find whether any of the (distant) nodes in the network has seen same/similar object before (b)There are two phases in object matching Learning phase Matching phase q Learning phase: compact representation (model) of the object is extracted from one or more images and stored q Matching phase: same compact representation of an object is extracted from the newly acquired image.

(C) we could avoid the distribution of complete feature vectors through a hierarchical encoding scheme. Hierarchical encoding scheme is based on a hierarchical reduction of feature vectors. We require that the primary node retains the complete information about the object (e. g. an unmodified feature vector) Its neighbors receive less detailed, more abstract information, which generally requires less storage and transmission capacity. In this way, the amount of data transmitted across, or stored in the network, can be significantly reduced

Questoin 2: ((a)What is difference between flooding-at-match and flooding at learn? (b)What are the drawbacks of M-hier and how we can improve M-hier? Ans: (a) Flooding –at –match : Ø Captured visual information is stored locally and each task of finding and object has to be broadcasted across the network by flooding, for each new image acquired. Ø Distribution requires little or no network traffic during the learning phase , however it produces a large amount of data transmitted in the matching phase Flooding-at-learn: Ø Captured visual information from each sensor is distributed to all the nodes for local storage. Again flooding is used for this purpose. Diction of similar objects is then performed locally by each sensor as new images are acquired Ø Compare to fooling –at -match large amount of data transmitted during the learning phase and distribution requires very little or no traffic during the matching phase

(a) Drawbacks: Ø M-hier is not sufficiently scalable. Ø It is still based on flooding the whole network, which consumes bandwidth despite reducing level information. (b)Improvement for M-hier is Q-hier: Feature vectors of detected object are distributed in its column only, in the same way, instead of whole network. Flooding avoided in whole network.

Question 3 In which situation matching would be find in Q-hier ? Show with diagram or explain in words? Ans: q Feature vectors of detected object are propagated in its column only, in the same way, instead of whole network. q Search is then performed in the row, by transmitting the lowest level 1 feature vector. q At intersecting row and column called “rendezvous” node, matching can be made at level available there. q If no match, search stops.

Diagram shows that the matching at the intersection D S