INTRODUCTION DATA STRUCTURES AND ALGORITHMS www asyrani comdata

INTRODUCTION DATA STRUCTURES AND ALGORITHMS www. asyrani. com/data

1 Please forget that you get low/high marks for C Programming class Set up in your mind right now, this subject is the most interesting!!! 3 Things you must have: a) Visual C++ 2010 Edition b) Internet Access!!! (Most important one) 2

Programming is not hard as you think!!!

Don’t remember theory but remember how it works

• Phone number • 0137771180 • asyrani@utem. edu. my

Things you need to do • First go to www. asyrani. com/teaching

Laman Struktur Data • Link http: //asyrani. com/data

FIRST GLANCE OVERVIEW

Over the view …Overview • How to create Windows 8 anyone?

I know!!!!!! We need manpower!!! Computer engineers “I will make sure that the software can be integrated with the specific hardware” = Programmers “I’m the one that do the programming stuff” Designers “I design the interface and give the Windows 8 nice looks”

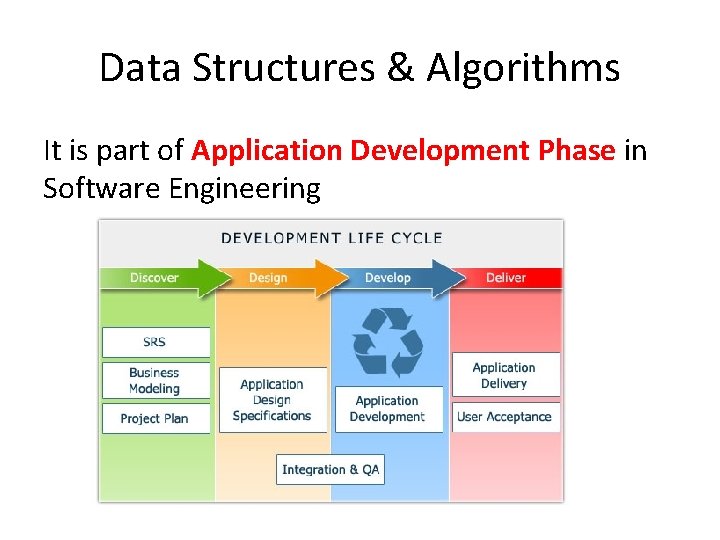
Data Structures & Algorithms It is part of Application Development Phase in Software Engineering

Why it is important? DATA STRUCTURES & ALGORITHMS

Why it is so important Computer Utilization – Consumers: control washing machine, oven, cars. – Engineers & scientist: design, model, simulate. – Commerce: financial transaction, communications. Modern Computers • Store, analyze, search, transfer and update huge collections of complex data.

Why it is so important (2) Increase efficiency of the simulation Organize and access data quickly and smoothly

GOOD QUESTION WHY WE NEED TO STUDY ‘EM?

WHY I NEED TO STUDY THIS? BECAUSE ONE OF YOUR SUBJECT AND YOU ARE BORN TO BE LEARNED THIS SUBJECT!!!

WHY I NEED TO STUDY THIS? WITHOUT Data Structures and Algorithms WITH Data Structures and Algorithms

OR TO PUT IT INTO WORDS WITHOUT Data Structures and Algorithms WITH Data Structures and Algorithms Slow Too much codes Messy code No one can understand your code • Not efficient although it can be running correctly • Eat up your computer memory too much • • Fast Simple and short codes Clean code Most will understand your code • Efficient and can be running smoothly • Memory efficient • Eliminate unnecessary loops and operations.

Now for serious learning avtivity DATA STRUCTURES AND ALGORITHM DEFINITION

Programming is easy as eating a pancake Do you know how to eat? Don’t cha? ?

DIFFERENCES BETWEEN C++ AND C

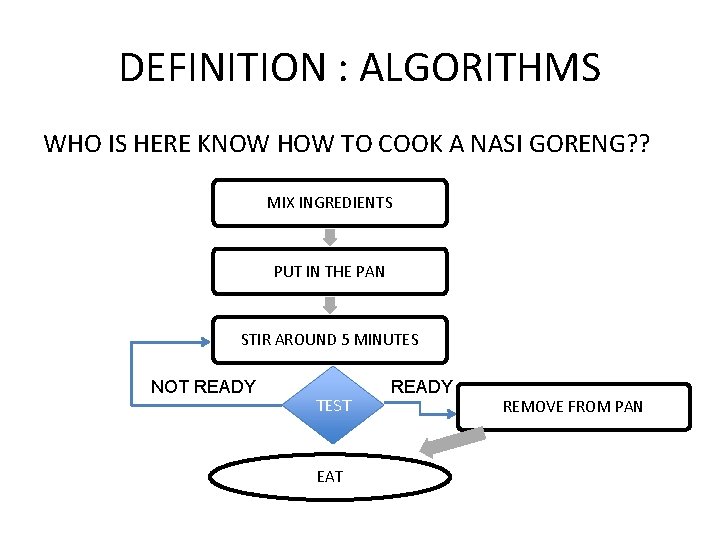
DEFINITION : ALGORITHMS WHO IS HERE KNOW HOW TO COOK A NASI GORENG? ? MIX INGREDIENTS PUT IN THE PAN STIR AROUND 5 MINUTES NOT READY TEST EAT READY REMOVE FROM PAN

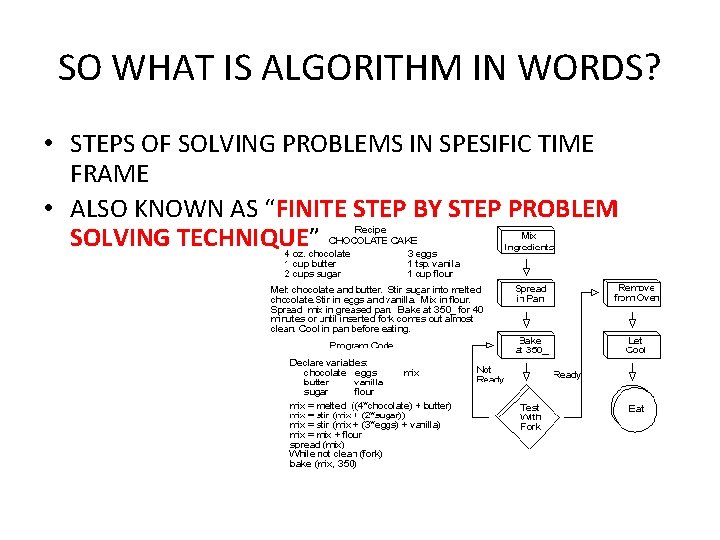
SO WHAT IS ALGORITHM IN WORDS? • STEPS OF SOLVING PROBLEMS IN SPESIFIC TIME FRAME • ALSO KNOWN AS “FINITE STEP BY STEP PROBLEM SOLVING TECHNIQUE”

GOOD ALGORITHMS • Simple, clear, concise and readable. • Solvable, terminates after a finite number of instructions. • Correct, efficient and robust. • Accomplish at least one task or produce at least one output.

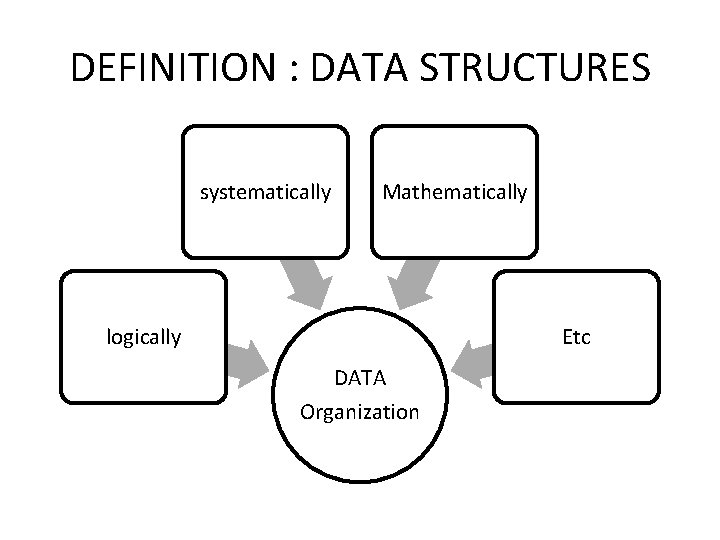
DEFINITION : DATA STRUCTURES systematically Mathematically logically Etc DATA Organization

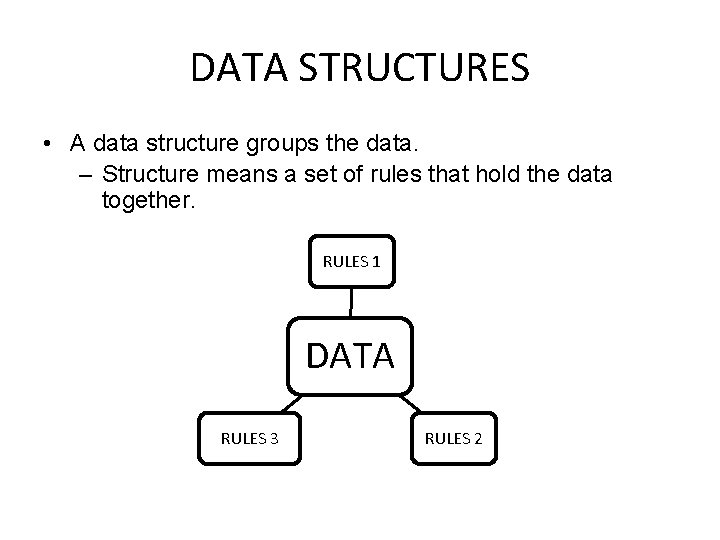
DATA STRUCTURES • A data structure groups the data. – Structure means a set of rules that hold the data together. RULES 1 DATA RULES 3 RULES 2

ALGORITHM ANALYSIS

Why Algorithm analysis Generally, we use a computer because we need to process a large amount of data. When we run a program on large amounts of input, besides to make sure the program is correct, we must be certain that the program terminates within a reasonable amount of time.

What is Algorithm Analysis? Algorithm: A clearly specified finite set of instructions a computer follows to solve a problem. Algorithm analysis: a process of determining the amount of time, resource, etc. required when executing an algorithm.

BIG O NOTATION

Big Oh Notation • Big Oh notation is used to capture the most dominant term in a function, and to represent the growth rate. • Also called asymptotic upper bound. Ex: 100 n 3 + 30000 n =>O(n 3) 100 n 3 + 2 n 5+ 30000 n =>O(n 5)

Upper and lower bounds of a function

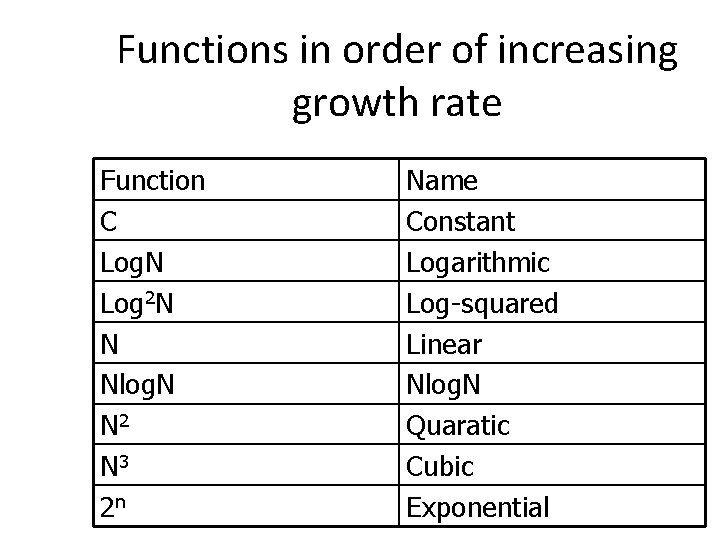
Functions in order of increasing growth rate Function C Log. N Log 2 N N Nlog. N N 2 N 3 2 n Name Constant Logarithmic Log-squared Linear Nlog. N Quaratic Cubic Exponential

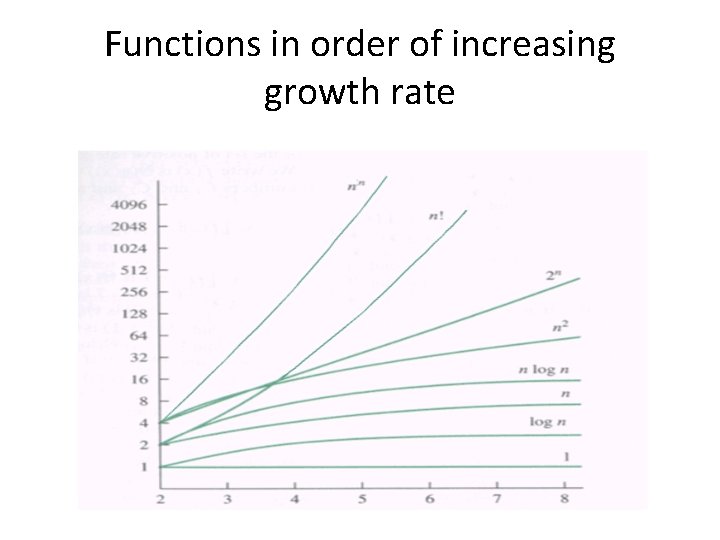
Functions in order of increasing growth rate

Examples of Algorithm Running Times • Min element in an array : O(n) • Closest points in the plane, ie. Smallest distance pairs: n(n-1)/2 => O(n 2) • Colinear points in the plane, ie. 3 points on a straight line: n(n-1)(n-2)/6 => O(n 3)

The Max. Contiguous Subsequence In computer science, the maximum subarray problem is the task of finding the contiguous subarray within a one-dimensional array of numbers (containing at least one positive number) which has the largest sum. For example, for the sequence of values − 2, 1, − 3, 4, − 1, 2, 1, − 5, 4; the contiguous subarray with the largest sum is 4, − 1, 2, 1, with sum 6.

The Max. Contiguous Subsequence • EXAMPLE • {-2, 11, -4, 13, -5, 2} =>20 • {1, -3, 4, -2, -1, 6} => 7

Brute Force Algorithm O(n 2) template <class Comparable> Comparable max. Sub. Sum(const vector<Comparable> a, int & seq. Start, int & seq. End){ int n = a. size(); Comparable max. Sum = 0; for(int i = 0; i < n; i++){ // for each possible start point for(int j = i; j < n; j++){ // for each possible end point Comparable this. Sum = 0; for(int k = i; k <= j; k++) this. Sum += a[k]; //dominant term if( this. Sum > max. Sum){ max. Sum = this. Sum; seq. Start = i; seq. End = j; } } } return max. Sum; } //A cubic maximum contiguous subsequence sum algorithm

O(n 3) Algorithm Analysis • We do not need precise calculations for a Big. Oh estimate. In many cases, we can use the simple rule of multiplying the size of all the nested loops

O(n 2) algorithm • An improved algorithm makes use of the fact that • If we have already calculated the sum for the subsequence i, …, j-1. Then we need only one more addition to get the sum for the subsequence i, …, j. However, the cubic algorithm throws away this information. • If we use this observation, we obtain an improved algorithm with the running time O(N 2).

O(N 2) Algorithm cont. template <class Comparable> Comparable max. Subsequence. Sum(const vector<Comparable>& a, int & seq. Start, int &seq. End){ int n = a. size(); Comparable max. Sum = 0; for( int i = 0; i < n; i++){ Comparable this. Sum = 0; for( int j = i; j < n; j++){ this. Sum += a[j]; if( this. Sum > max. Sum){ max. Sum = this. Sum; seq. Start = i; seq. End = j; } } } return max. Sum; }

O(N) Algorithm template <class Comparable> Comparable max. Subsequence. Sum(const vector<Comparable>& a, int & seq. Start, int &seq. End){ int n = a. size(); Comparable this. Sum = 0, max. Sum = 0; int i=0; for( int j = 0; j < n; j++){ this. Sum += a[j]; if( this. Sum > max. Sum){ max. Sum = this. Sum; seq. Start = i; seq. End = j; }else if( this. Sum < 0) { i = j + 1; this. Sum = 0; } } return max. Sum; }

Sequential Search • A sequential search steps through the data sequentially until an match is found. • A sequential search is useful when the array is not sorted. • A sequential search is linear O(n) (i. e. proportional to the size of input) – Unsuccessful search --- n times – Successful search (worst) --- n times – Successful search (average) --- n/2 times

Binary Search • If the array has been sorted, we can use binary search, which is performed from the middle of the array rather than the end. • We keep track of low_end and high_end, which delimit the portion of the array in which an item, if present, must reside. • If low_end is larger than high_end, we know the item is not present.

6. 8 Limitations of Big-Oh Analysis • Big-Oh is an estimate tool for algorithm analysis. It ignores the costs of memory access, data movements, memory allocation, etc. => hard to have a precise analysis. Ex: 2 nlogn vs. 1000 n. Which is faster? => it depends on n

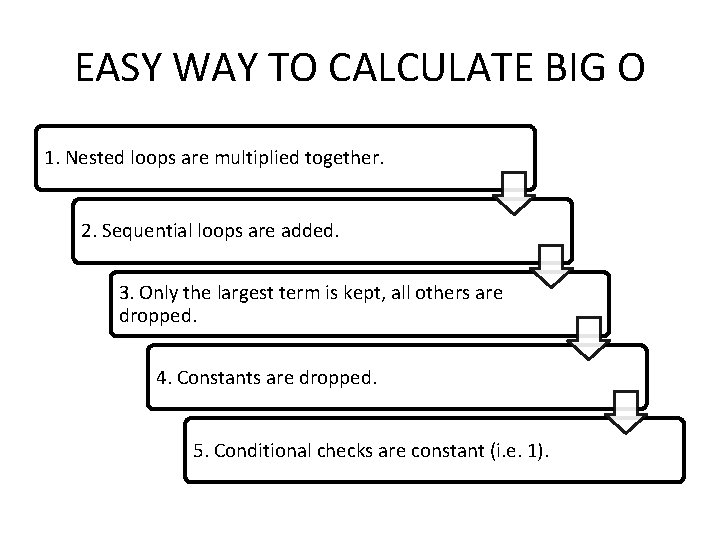
EASY WAY TO CALCULATE BIG O 1. Nested loops are multiplied together. 2. Sequential loops are added. 3. Only the largest term is kept, all others are dropped. 4. Constants are dropped. 5. Conditional checks are constant (i. e. 1).

LET’S RIDE Here we iterate 'n' times. Since nothing else is going on inside the loop (other then constant time printing), this algorithm is said to be O(n).

LET’S RIDE Each loop is 'n'. Since the inner loop is nested, it is n*n, thus it is O(n^2). Hardly efficient. We can make it a bit better by doing the following:

LET’S RIDE Outer loop is still 'n'. The inner loop now executes 'i' times, the end being (n-1). We now have (n(n-1)). This is still in the bound of O(n^2), but only in the worst case.

LET’S RIDE At first you might say that the upper bound is O(2 n); however, we drop constants so it becomes O(n). Mathematically, they are the same since (either way) it will require 'n' elements iterated (even though we'd iterate 2 n times).

LET’S RIDE You wouldn't do this exact example in implementation, but doing something similar certainly is in the realm of possibilities. In this case we add each loop's Big O, in this case n+n^2. O(n^2+n) is not an acceptable answer since we must drop the lowest term. The upper bound is O(n^2). Why? Because it has the largest growth rate (upper bound or limit for the Calculus inclined).

LET’S RIDE Outer loop is 'n', inner loop is 2, this we have 2 n, dropped constant gives up O(n).

LET’S RIDE There are n iterations, however, instead of simply incrementing, 'i' is increased by 2*itself each run. Thus the loop is log(n).

LET’S RIDE This example is n*log(n). (Remember that nested loops multiply their Big O's. )

CONCLUSION OF BIG O • In short Big O is simply a way to measure the efficiency of an algorithm. The goal is constant or linear time, thus the various data structures and their implementations. • Keep in mind that a "faster" structure or algorithm is not necessary better. • For example, see the classic hash table versus binary tree debate. While not 100% factual, it often said that a a hash-table is O(1) and is therefore better then a tree. REFERENCE: http: //www. dreamincode. net/forums/topic/125427 -determining-big-onotation/

What we will learn? ? ? TYPES OF DATA STRUCTURES

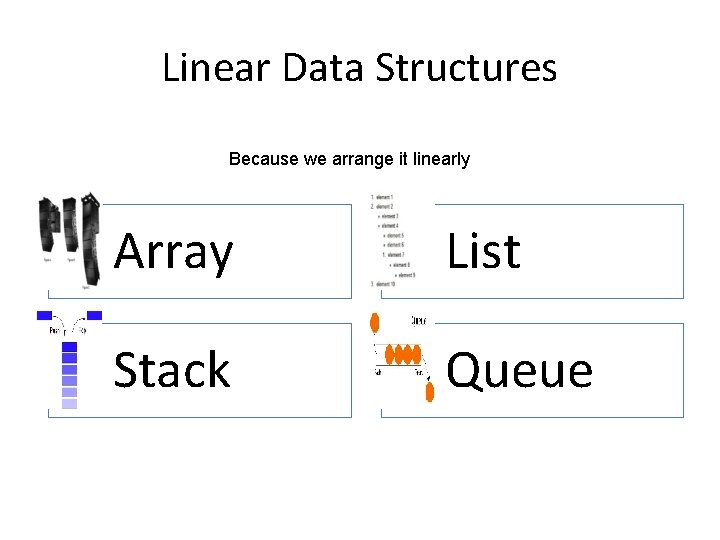
Linear Data Structures Because we arrange it linearly Array List Stack Queue

Non-Linear Data Structures The data is not necessarily need to arrange in order Graph Trees

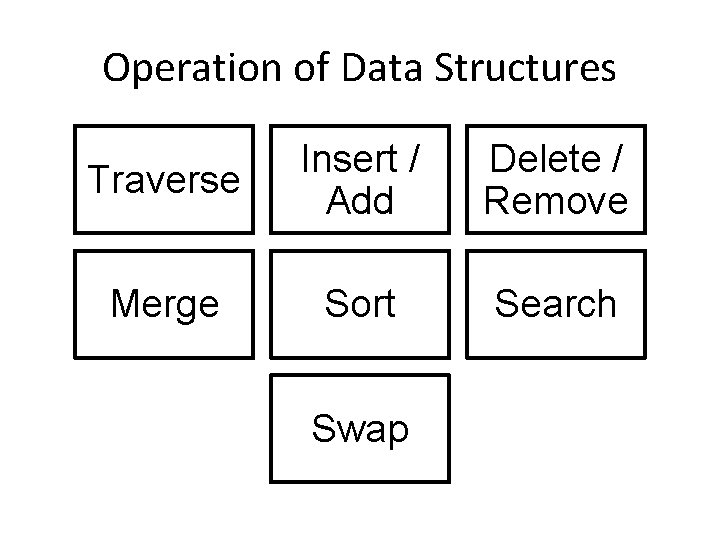
Operation of Data Structures Traverse Insert / Add Delete / Remove Merge Sort Search Swap

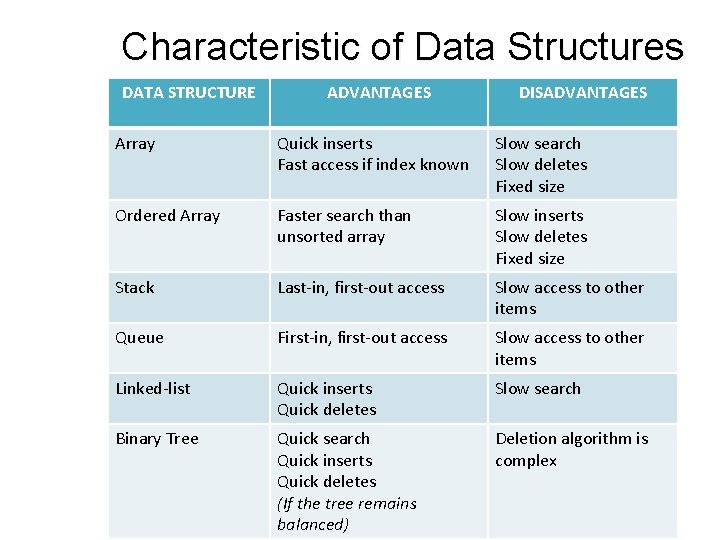
Characteristic of Data Structures DATA STRUCTURE ADVANTAGES DISADVANTAGES Array Quick inserts Fast access if index known Slow search Slow deletes Fixed size Ordered Array Faster search than unsorted array Slow inserts Slow deletes Fixed size Stack Last-in, first-out access Slow access to other items Queue First-in, first-out access Slow access to other items Linked-list Quick inserts Quick deletes Slow search Binary Tree Quick search Quick inserts Quick deletes (If the tree remains balanced) Deletion algorithm is complex

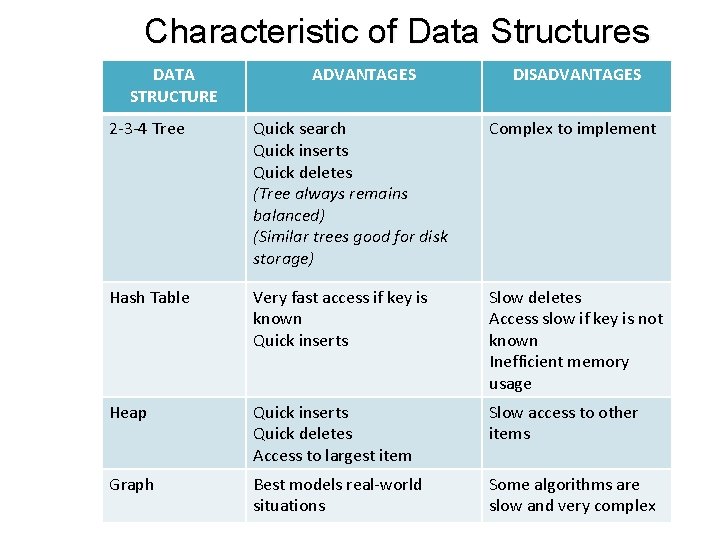
Characteristic of Data Structures DATA STRUCTURE ADVANTAGES DISADVANTAGES 2 -3 -4 Tree Quick search Quick inserts Quick deletes (Tree always remains balanced) (Similar trees good for disk storage) Complex to implement Hash Table Very fast access if key is known Quick inserts Slow deletes Access slow if key is not known Inefficient memory usage Heap Quick inserts Quick deletes Access to largest item Slow access to other items Graph Best models real-world situations Some algorithms are slow and very complex

Move into the next one DATA TYPE

DATA TYPE • The basic stuff. What do you need to have before cooking nasi goreng? – Nasi putih – Perencah Adabi – Ikan bilis • But how much? – Nasi putih around 600 gram – Perencah Adabi around 30. 5 gram – 30 – 40 ikan bilis

DATA TYPE • The basic stuff. What do you need to have before cooking nasi goreng? – Nasi putih – Perencah Adabi – Ikan bilis • But how much? This is what we’ve called Data Type – Nasi putih around 600 gram – Perencah Adabi around 30. 5 gram – 30 – 40 ikan bilis • Data type of a variable is the set of values that the variable may assume. • Basic Data Types in C++ : int , char , double, String, Boolean, etc.

Now let us look deeper ABSTRACT DATA TYPE (ADT)

Before we proceed • I know you guys want to know whether you guys need to memorize all this stuff or not • To be honest. I’ve never memorize all things that I do not use. Even terms etc • But because YOU ARE STUDENT, you guys still need to memorize some facts because you have quizzes, test(s) and final exam to consider.

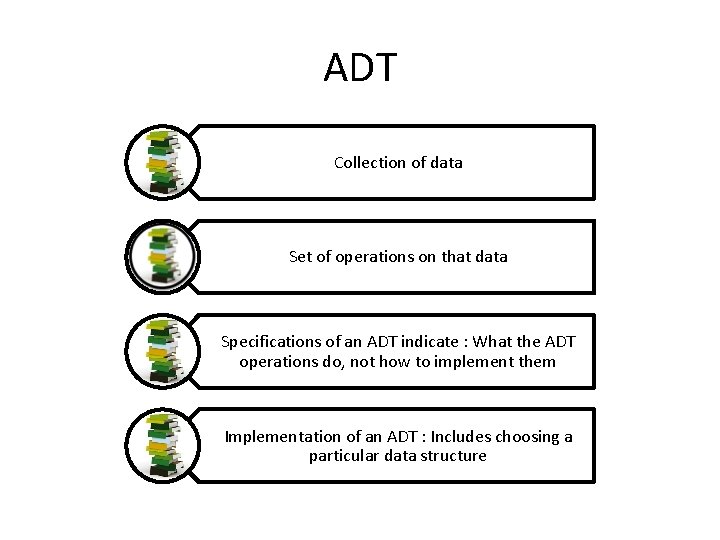
ADT Collection of data Set of operations on that data Specifications of an ADT indicate : What the ADT operations do, not how to implement them Implementation of an ADT : Includes choosing a particular data structure

ADT(2) C++ and JAVA (because of classes system) -> ADT Example of EDT : Stack and Queue

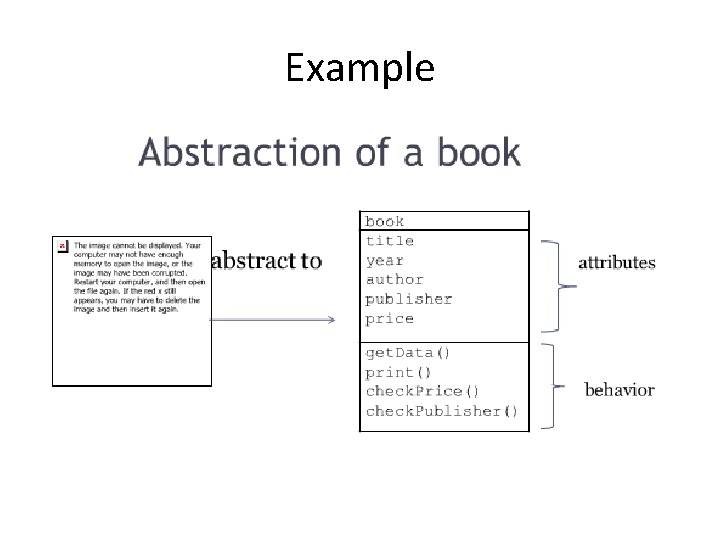
Example

ADT and Data Structures? • A Data Structure is an implementation of an ADT. That is it is a translation of ADT into statements of a programming language. It consists of: – The declarations that define a variable to be of that ADT type. – The operations defined on the ADT(using procedures of the programming language). • An ADT implementation chooses a data structure to represent the ADT • Each data structure is built up from the basic data types of the underlying programming language using the available data structuring facilities , such as arrays, pointers , files , sets, etc.

Example: • A ” Queue ” is an abstract data type which can be defined as a sequence of elements with operations such as Enqueue(x, q), Dequeue(q). This can be implemented using data structures such as: – Array – Singly linked list – Doubly linked list – Circular array

Key words: • Data Structures & Algorithms – Definition – A data structure is an arrangement of data in a computer's memory or even disk storage. An example of several common data structures are arrays, linked lists, queues, stacks, binary trees, and hash tables. – Algorithms, on the other hand, are used to manipulate the data contained in these data structures as in searching and sorting. Many algorithms apply directly to a specific data structures. When working with certain data structures you need to know how to insert new data, search for a specified item, and deleting a specific item.

Key words: �Data types ◦ When we consider a primitive type we are actually referring to two things: a data item with certain characteristics and the permissible operations on that data ◦ The data type's permissible operations are an inseparable part of its identity; understanding the type means understanding what operations can be performed on it �Example: ◦ An int in Java or C++, for example, can contain any wholenumber value from -2, 147, 483, 648 to +2, 147, 483, 647. It can also be used with the operators +, -, *, and /

Key words: �Abstract Data Type (ADT) ◦ Is a class considered without regard to its implementation. ◦ It can be thought of as a "description" of the data in the class and a list of operations that can be carried out on that data and instructions on how to use these operations. ◦ An end user (or class user), you should be told what methods to call, how to call them, and the results that should be expected, but not HOW they work. �Consider for example the stack class. ◦ The end user knows that push() and pop() exist and how they work. ◦ The user doesn't and shouldn't have to know how push() and pop() work, or whether data is stored in an array, a linked list, or some other data structure like a tree.

Next Class: • Chapter 2 (part 1) – Introduction to C++ – Programming fundamentals

Note • Always browse to www. asyrani. com/data • Wait for further updated information in my website You are encouraged to collaborate in study groups. But you cannot directly copy or slightly change other students’ solutions or code