Introduction CSCE 235 Introduction to Discrete Structures Spring












- Slides: 13

Introduction CSCE 235 Introduction to Discrete Structures Spring 2010 Instructor: Berthe Y. Choueiry (Shu-we-ri) GTA: Nobel Khandaker http: //cse. unl. edu/~choueiry/F 10 -235/ http: //cse. unl. edu/~cse 235/

Outline • Introduction: syllabus, schedule, web, topics • Why Discrete Mathematics? • Basic preliminaries CSCE 235, Spring 2010 Introduction 2

Introduction • • • Roll Syllabus Lectures: M/W/F 12: 30— 1: 20 pm (Avery 119) Recitations: M 3: 30— 4: 20 pm (Avery 110) Office hours: – Instructor: M/W 1: 30— 2: 30 pm (Avery 360) – TA: Tue/Thu 9: 00— 10: 00 am (Student Res. Center) • • Must have a cse account Must use cse handin Bonus points: report bugs Web page CSCE 235, Spring 2010 Introduction 3

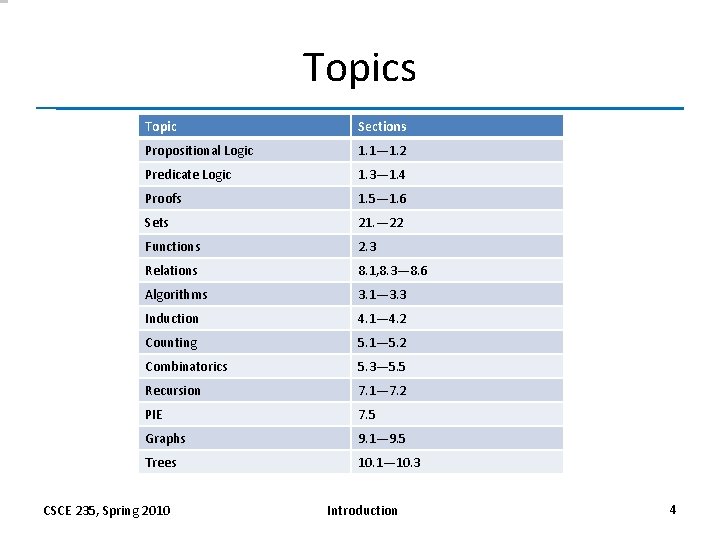
Topics Topic Sections Propositional Logic 1. 1— 1. 2 Predicate Logic 1. 3— 1. 4 Proofs 1. 5— 1. 6 Sets 21. — 22 Functions 2. 3 Relations 8. 1, 8. 3— 8. 6 Algorithms 3. 1— 3. 3 Induction 4. 1— 4. 2 Counting 5. 1— 5. 2 Combinatorics 5. 3— 5. 5 Recursion 7. 1— 7. 2 PIE 7. 5 Graphs 9. 1— 9. 5 Trees 10. 1— 10. 3 CSCE 235, Spring 2010 Introduction 4

Why Discrete Mathematics? (I) • Computers use discrete structures to represent and manipulate data. • CSE 235 and CSE 310 are the basic building block for becoming a Computer Scientist • Computer Science is not Programming • Computer Science is not Software Engineering • Edsger Dijkstra: “Computer Science is no more about computers than Astronomy is about telescopes. ” • Computer Science is about problem solving. CSCE 235, Spring 2010 Introduction 5

Why Discrete Mathematics? (II) • Mathematics is at the heart of problem solving • Defining a problem requires mathematical rigor • Use and analysis of models, data structures, algorithms requires a solid foundation of mathematics • To justify why a particular way of solving a problem is correct or efficient (i. e. , better than another way) requires analysis with a welldefined mathematical model. CSCE 235, Spring 2010 Introduction 6

Problem Solving requires mathematical rigor • Your boss is not going to ask you to solve – an MST (Minimal Spanning Tree) or – a TSP (Travelling Salesperson Problem) • Rarely will you encounter a problem in an abstract setting • However, he/she may ask you to build a rotation of the company’s delivery trucks to minimize fuel usage • It is up to you to determine – a proper model for representing the problem and – a correct or efficient algorithm for solving it CSCE 235, Spring 2010 Introduction 7

Scenario I • A limo company has hired you/your company to write a computer program to automate the following tasks for a large event • Task 1: In the first scenario, businesses request – limos and drivers – for a fixed period of time, specifying a start data/time and end date/time and – a flat charge rate • The program must generate a schedule that accommodates the maximum number of customers CSCE 235, Spring 2010 Introduction 8

Scenario II • Task 2: In the second scenario – the limo service allows customers to bid on a ride – so that the highest bidder get a limo when there aren’t enough limos available • The program should make a schedule that – Is feasible (no limo is assigned to two or more customers at the same time) – While maximizing the total profit CSCE 235, Spring 2010 Introduction 9

Scenario III • Task 3: Here each customer – is allowed to specify a set of various times and – bid an amount for the entire event. – The limo service must choose to accept the entire set of times or reject it • The program must again maximize the profit. CSCE 235, Spring 2010 Introduction 10

What’s your job? • Build a mathematical model for each scenario • Develop an algorithm for solving each task • Justify that your solutions work – Prove that your algorithms terminate. Termination – Prove that your algorithms find a solution when there is one. Completeness – Prove that the solution of your algorithms is correct Soundness – Prove that your algorithms find the best solution (i. e. , maximize profit). Optimality (of the solution) – Prove that your algorithms finish before the end of life on earth. Efficiency, time & space complexity CSCE 235, Spring 2010 Introduction 11

The goal of this course • Give you the foundations that you will use to eventually solve these problems. – Task 1 is easily (i. e. , efficiently) solved by a greedy algorithm – Task 2 can also be (almost) easily solved, but requires a more involved technique, dynamic programming – Task 3 is not efficiently solvable (it is NP-hard) by any known technique. It is believed today that to guarantee an optimal solution, one needs to look at all (exponentially many) possibilities CSCE 235, Spring 2010 Introduction 12

Basic Preliminaries • A set is a collection of objects. • For example: – S = {s 1, s 2, s 3, …, sn} is a finite set of n elements – S = {s 1, s 2, s 3, …} is a infinite set of elements. • s 1 S denotes that the object s 1 is an element of the set S • s 1 S denotes that the object s 1 is not an element of the set S • La. Tex – $S={s_1, s_2, s_3, ldots, s_n}$ – $s_i in S$ – $si notin S$ CSCE 235, Spring 2010 Introduction 13