Introduction CHAPTER 1 1 What is a signal

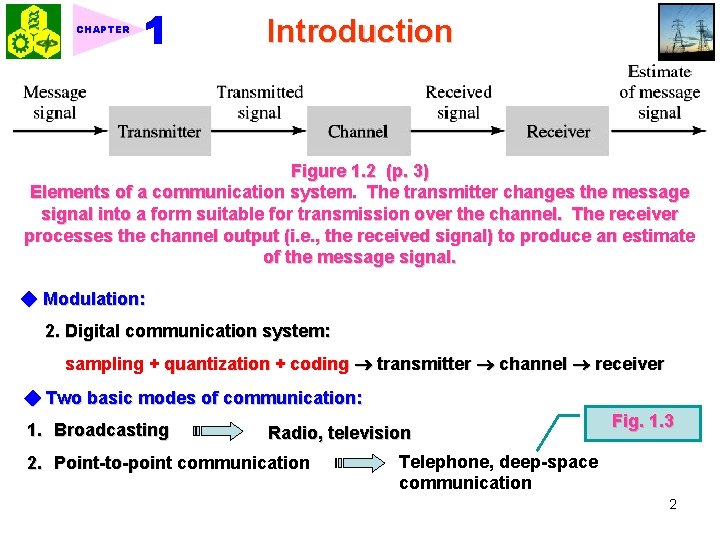
Introduction CHAPTER 1. 1 What is a signal? A signal is formally defined as a function of one or more variables that conveys information on the nature of a physical phenomenon. 1. 2 What is a system? A system is formally defined as an entity that manipulates one or more signals to accomplish a function, thereby yielding new signals. Figure 1. 1 (p. 2) Block diagram representation of a system. 1. 3 Overview of Specific Systems ★ 1. 3. 1 Communication systems Elements of a communication system Fig. 1. 2 1. Analog communication system: modulator + channel + demodulator 1

CHAPTER Introduction Figure 1. 2 (p. 3) Elements of a communication system. The transmitter changes the message signal into a form suitable for transmission over the channel. The receiver processes the channel output (i. e. , the received signal) to produce an estimate of the message signal. ◆ Modulation: 2. Digital communication system: sampling + quantization + coding transmitter channel receiver ◆ Two basic modes of communication: 1. Broadcasting Radio, television 2. Point-to-point communication Fig. 1. 3 Telephone, deep-space communication 2

CHAPTER Introduction Figure 1. 3 (p. 5) (a) Snapshot of Pathfinder exploring the surface of Mars. (b) The 70 -meter (230 -foot) diameter antenna located at Canberra, Australia. The surface of the 70 -meter reflector must remain accurate within a fraction of the signal’s wavelength. (Courtesy of Jet Propulsion Laboratory. ) 3

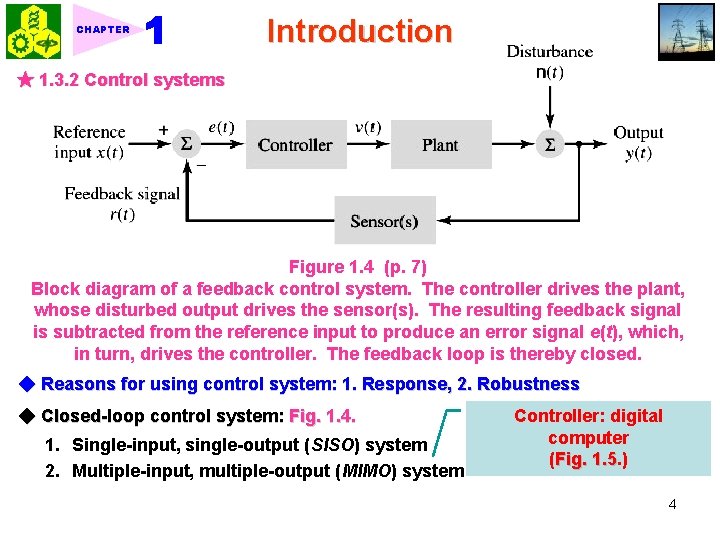
CHAPTER Introduction ★ 1. 3. 2 Control systems Figure 1. 4 (p. 7) Block diagram of a feedback control system. The controller drives the plant, whose disturbed output drives the sensor(s). The resulting feedback signal is subtracted from the reference input to produce an error signal e(t), which, in turn, drives the controller. The feedback loop is thereby closed. ◆ Reasons for using control system: 1. Response, 2. Robustness ◆ Closed-loop control system: Fig. 1. 4. 1. Single-input, single-output (SISO) system 2. Multiple-input, multiple-output (MIMO) system Controller: digital computer (Fig. 1. 5. ) 1. 5 4

CHAPTER Introduction Figure 1. 5 (p. 8) NASA space shuttle launch. (Courtesy of NASA. ) 5

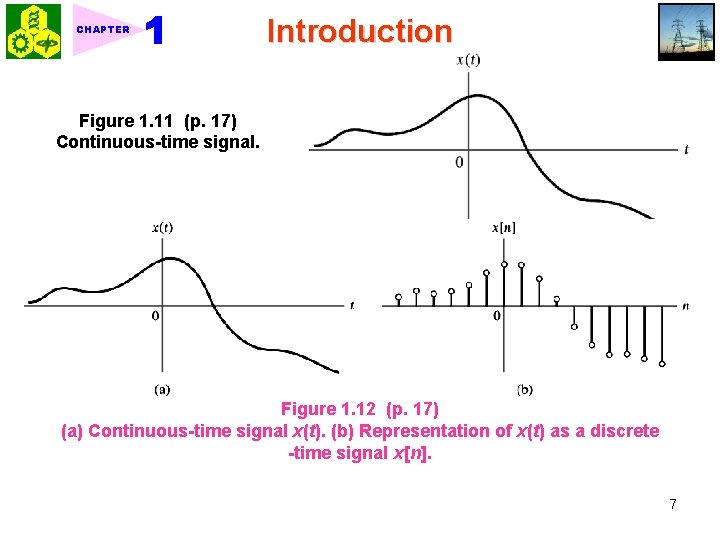
CHAPTER Introduction Analog Versus Digital Signal Processing Digital approach has two advantages over analog approach: 1. Flexibility 2. Repeatability 1. 4 Classification of Signals 1. Continuous-time and discrete-time signals Parentheses (‧) Continuous-time signals: x(t) Fig. 1 -11. (1. 1) where t = n. Ts Discrete-time signals: Fig. 1 -12. Brackets [‧] 6

CHAPTER Introduction Figure 1. 11 (p. 17) Continuous-time signal. Figure 1. 12 (p. 17) (a) Continuous-time signal x(t). (b) Representation of x(t) as a discrete -time signal x[n]. 7

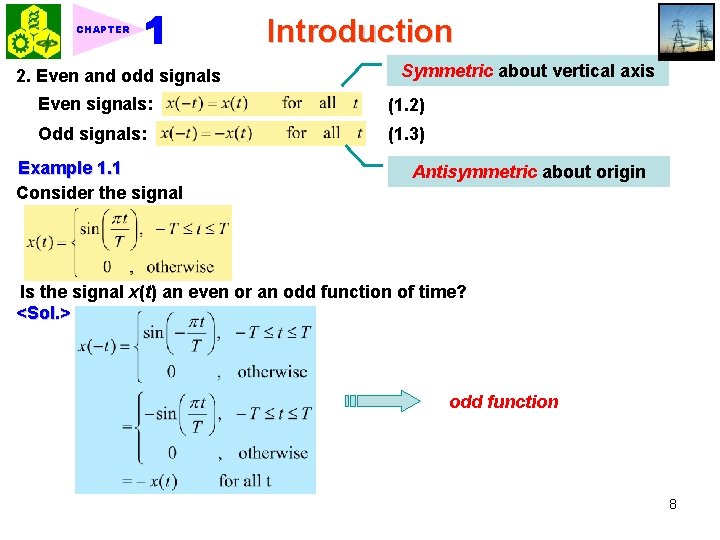
CHAPTER 2. Even and odd signals Introduction Symmetric about vertical axis Even signals: (1. 2) Odd signals: (1. 3) Example 1. 1 Consider the signal Antisymmetric about origin Is the signal x(t) an even or an odd function of time? <Sol. > odd function 8

CHAPTER Introduction ◆ Even-odd decomposition of x(t): where Example 1. 2 Find the even and odd components of the signal <Sol. > (1. 4) Even component: (1. 5) Odd component: 9

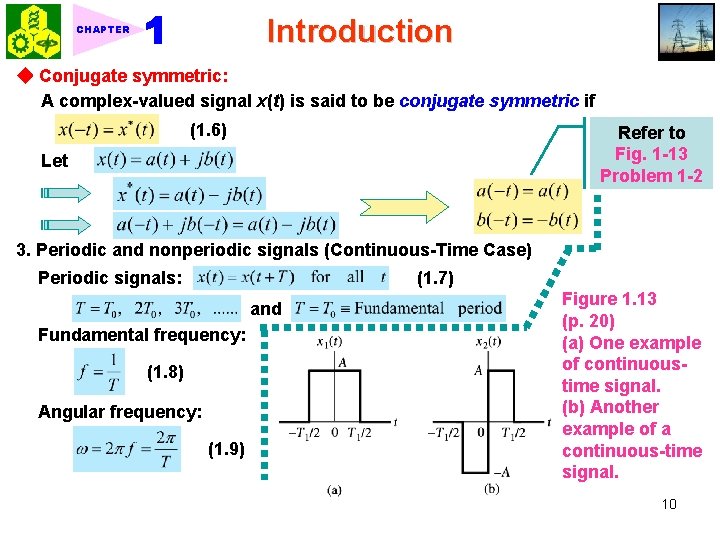
Introduction CHAPTER ◆ Conjugate symmetric: A complex-valued signal x(t) is said to be conjugate symmetric if (1. 6) Refer to Fig. 1 -13 Problem 1 -2 Let 3. Periodic and nonperiodic signals (Continuous-Time Case) (1. 7) Periodic signals: and Fundamental frequency: (1. 8) Angular frequency: (1. 9) Figure 1. 13 (p. 20) (a) One example of continuoustime signal. (b) Another example of a continuous-time signal. 10

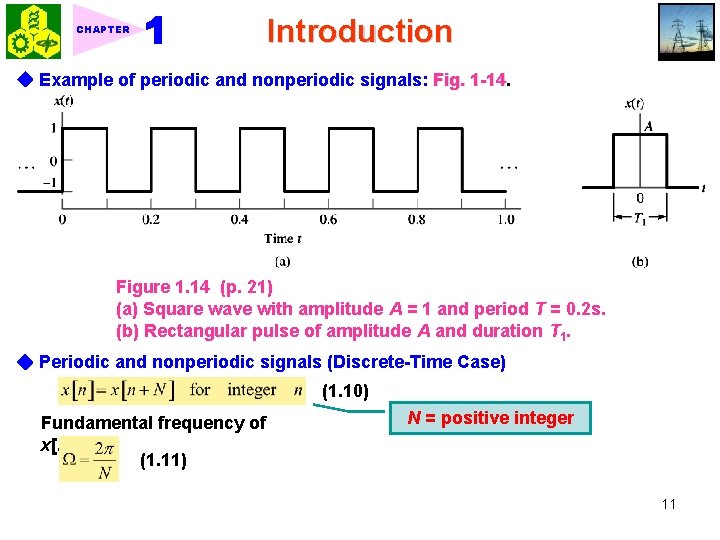
CHAPTER Introduction ◆ Example of periodic and nonperiodic signals: Fig. 1 -14 Figure 1. 14 (p. 21) (a) Square wave with amplitude A = 1 and period T = 0. 2 s. (b) Rectangular pulse of amplitude A and duration T 1. ◆ Periodic and nonperiodic signals (Discrete-Time Case) (1. 10) Fundamental frequency of x[n]: (1. 11) N = positive integer 11

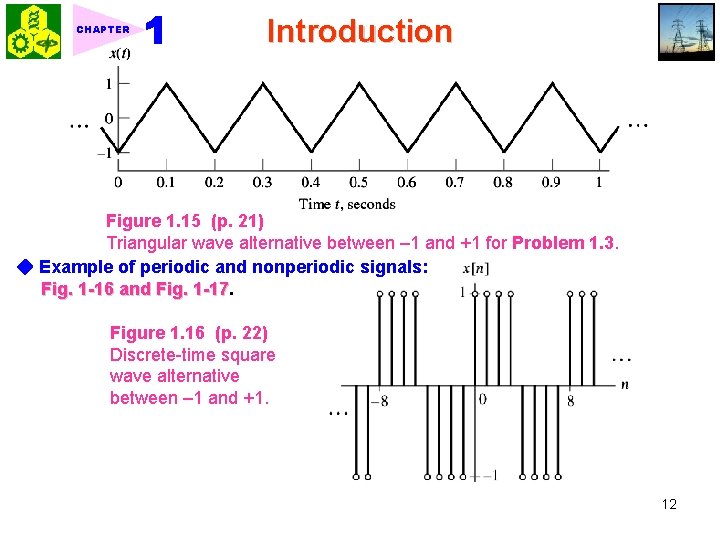
CHAPTER Introduction Figure 1. 15 (p. 21) Triangular wave alternative between – 1 and +1 for Problem 1. 3. ◆ Example of periodic and nonperiodic signals: Fig. 1 -16 and Fig. 1 -17 Figure 1. 16 (p. 22) Discrete-time square wave alternative between – 1 and +1. 12

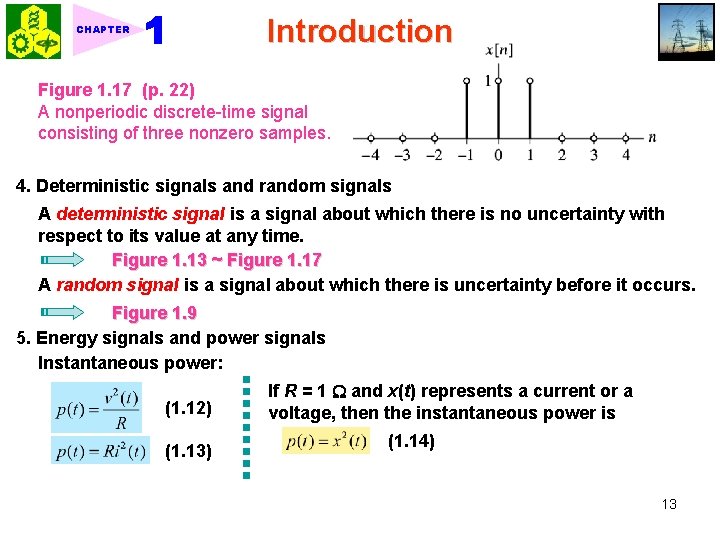
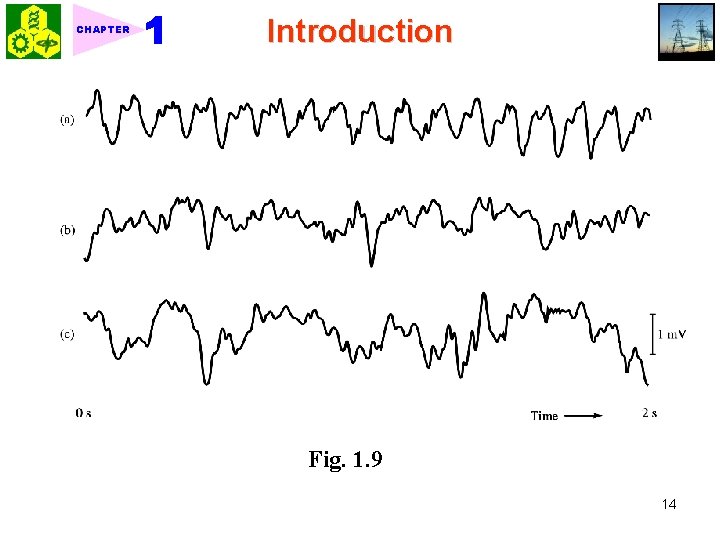
Introduction CHAPTER Figure 1. 17 (p. 22) A nonperiodic discrete-time signal consisting of three nonzero samples. 4. Deterministic signals and random signals A deterministic signal is a signal about which there is no uncertainty with respect to its value at any time. Figure 1. 13 ~ Figure 1. 17 A random signal is a signal about which there is uncertainty before it occurs. Figure 1. 9 5. Energy signals and power signals Instantaneous power: (1. 12) (1. 13) If R = 1 and x(t) represents a current or a voltage, then the instantaneous power is (1. 14) 13

CHAPTER Introduction Fig. 1. 9 14

Introduction CHAPTER The total energy of the continuous-time signal x(t) is (1. 15) ◆ Discrete-time case: Total energy of x[n]: (1. 18) Time-averaged, or average, power is (1. 16) Average power of x[n]: For periodic signal, the time-averaged power is (1. 19) (1. 17) ★ Energy signal: If and only if the total energy of the signal satisfies the condition (1. 20) ★ Power signal: If and only if the average power of the signal satisfies the condition 15

CHAPTER Introduction • Energy signal has zero time-average power (why? ) • Power signal has infinite energy (why? ) • Energy signal and power signal are mutually exclusive • Periodic signal and random signal are usually viewed as power signal • Nonperiodic and deterministic are usually viewed as energy signal 16

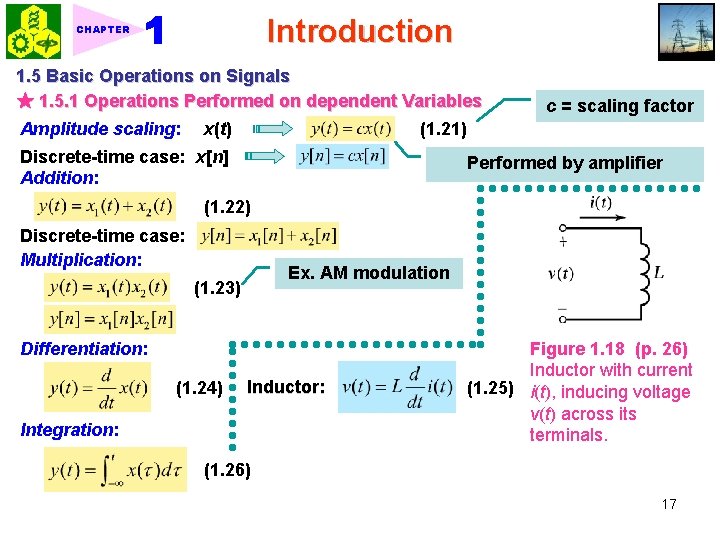
Introduction CHAPTER 1. 5 Basic Operations on Signals ★ 1. 5. 1 Operations Performed on dependent Variables Amplitude scaling: x(t) c = scaling factor (1. 21) Discrete-time case: x[n] Addition: Performed by amplifier (1. 22) Discrete-time case: Multiplication: Ex. AM modulation (1. 23) Differentiation: (1. 24) Inductor: Integration: Figure 1. 18 (p. 26) Inductor with current (1. 25) i(t), inducing voltage v(t) across its terminals. (1. 26) 17

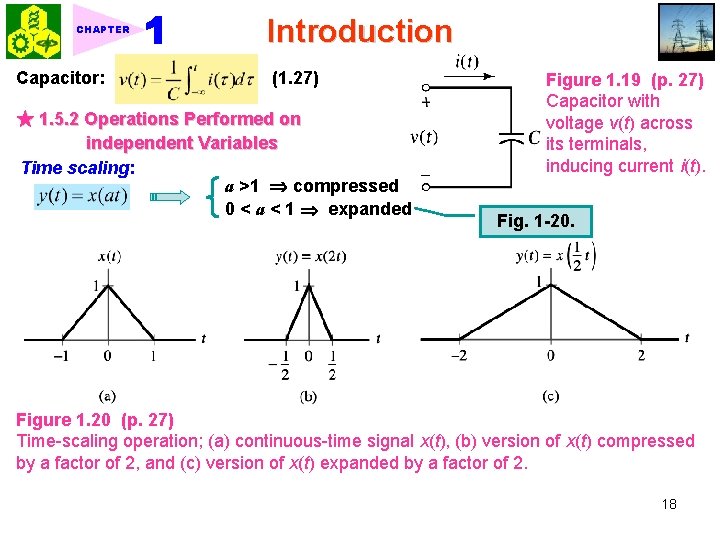
CHAPTER Capacitor: Introduction (1. 27) ★ 1. 5. 2 Operations Performed on independent Variables Time scaling: a >1 compressed 0 < a < 1 expanded Figure 1. 19 (p. 27) Capacitor with voltage v(t) across its terminals, inducing current i(t). Fig. 1 -20. Figure 1. 20 (p. 27) Time-scaling operation; (a) continuous-time signal x(t), (b) version of x(t) compressed by a factor of 2, and (c) version of x(t) expanded by a factor of 2. 18

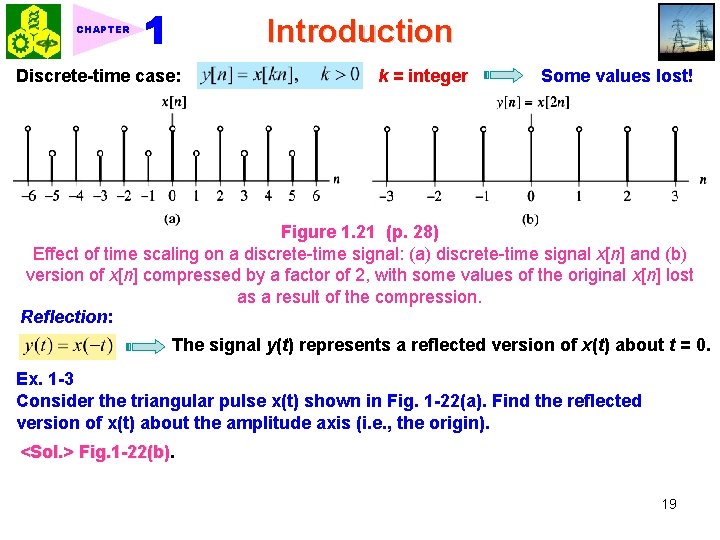
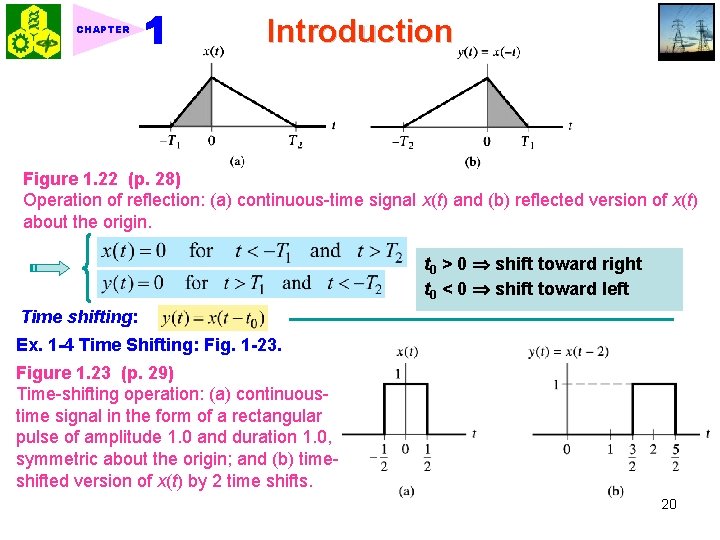
Introduction CHAPTER Discrete-time case: k = integer Some values lost! Figure 1. 21 (p. 28) Effect of time scaling on a discrete-time signal: (a) discrete-time signal x[n] and (b) version of x[n] compressed by a factor of 2, with some values of the original x[n] lost as a result of the compression. Reflection: The signal y(t) represents a reflected version of x(t) about t = 0. Ex. 1 -3 Consider the triangular pulse x(t) shown in Fig. 1 -22(a). Find the reflected version of x(t) about the amplitude axis (i. e. , the origin). <Sol. > Fig. 1 -22(b) 19

CHAPTER Introduction Figure 1. 22 (p. 28) Operation of reflection: (a) continuous-time signal x(t) and (b) reflected version of x(t) about the origin. t 0 > 0 shift toward right t 0 < 0 shift toward left Time shifting: Ex. 1 -4 Time Shifting: Fig. 1 -23. Figure 1. 23 (p. 29) Time-shifting operation: (a) continuoustime signal in the form of a rectangular pulse of amplitude 1. 0 and duration 1. 0, symmetric about the origin; and (b) timeshifted version of x(t) by 2 time shifts. 20

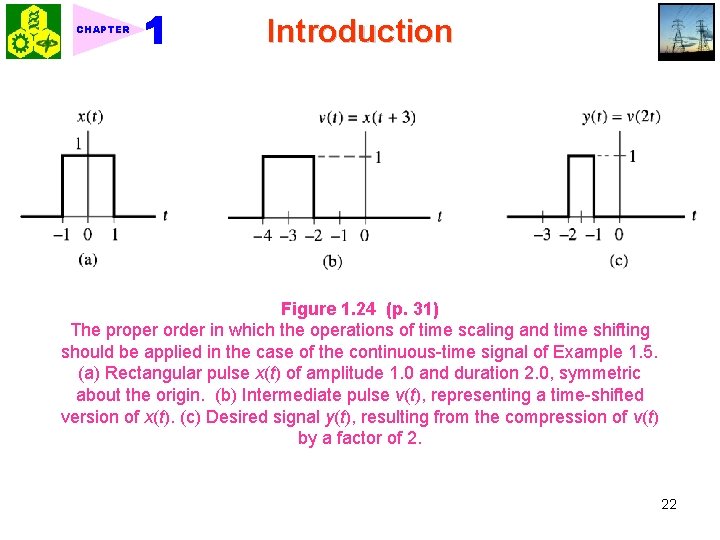
Introduction CHAPTER Discrete-time case: where m is a positive or negative integer ★ 1. 5. 3 Precedence Rule for Time Shifting and Time Scaling 1. Combination of time shifting and time scaling: (1. 28) (1. 29) (1. 30) 2. Operation order: To achieve Eq. (1. 28), 1 st step: time shifting 2 nd step: time scaling Ex. 1 -5 Precedence Rule for Continuous-Time Signal Consider the rectangular pulse x(t) depicted in Fig. 1 -24(a). Find y(t)=x(2 t + 3). <Sol. > Case 1: Fig. 1 -24. Shifting first, then scaling Case 2: Fig. 1 -25. Scaling first, then shifting 21

CHAPTER Introduction Figure 1. 24 (p. 31) The proper order in which the operations of time scaling and time shifting should be applied in the case of the continuous-time signal of Example 1. 5. (a) Rectangular pulse x(t) of amplitude 1. 0 and duration 2. 0, symmetric about the origin. (b) Intermediate pulse v(t), representing a time-shifted version of x(t). (c) Desired signal y(t), resulting from the compression of v(t) by a factor of 2. 22

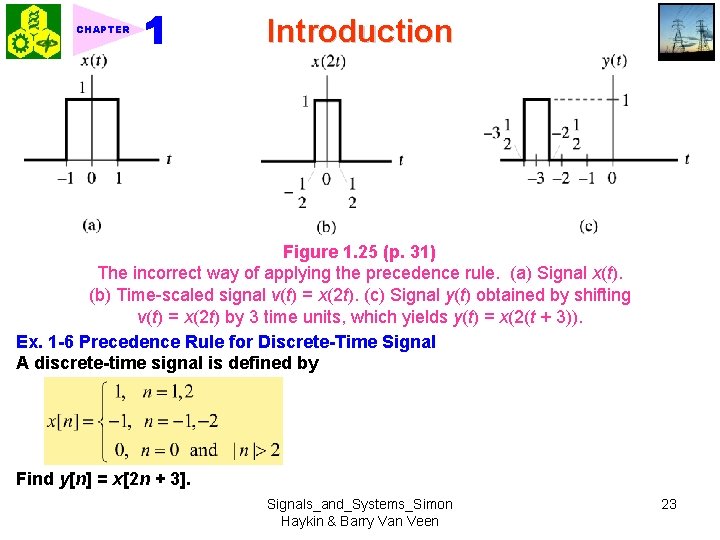
CHAPTER Introduction Figure 1. 25 (p. 31) The incorrect way of applying the precedence rule. (a) Signal x(t). (b) Time-scaled signal v(t) = x(2 t). (c) Signal y(t) obtained by shifting v(t) = x(2 t) by 3 time units, which yields y(t) = x(2(t + 3)). Ex. 1 -6 Precedence Rule for Discrete-Time Signal A discrete-time signal is defined by Find y[n] = x[2 n + 3]. Signals_and_Systems_Simon Haykin & Barry Van Veen 23

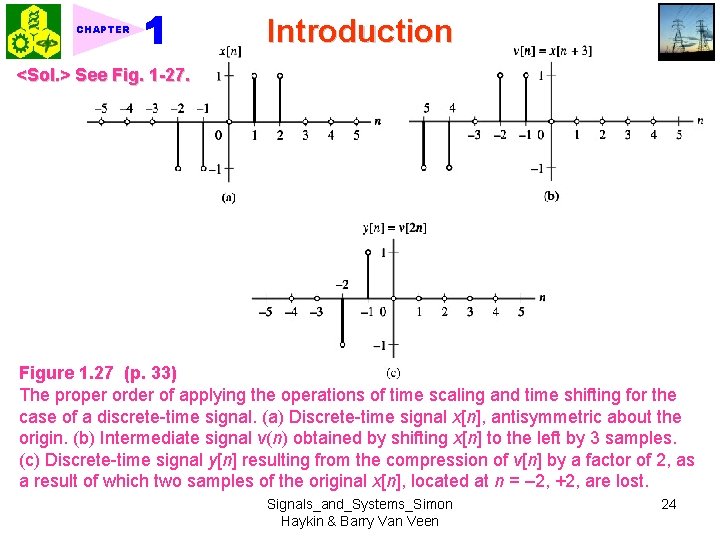
CHAPTER Introduction <Sol. > See Fig. 1 -27. Figure 1. 27 (p. 33) The proper order of applying the operations of time scaling and time shifting for the case of a discrete-time signal. (a) Discrete-time signal x[n], antisymmetric about the origin. (b) Intermediate signal v(n) obtained by shifting x[n] to the left by 3 samples. (c) Discrete-time signal y[n] resulting from the compression of v[n] by a factor of 2, as a result of which two samples of the original x[n], located at n = – 2, +2, are lost. Signals_and_Systems_Simon Haykin & Barry Van Veen 24