Introduction CHAPTER 1 1 What is a signal

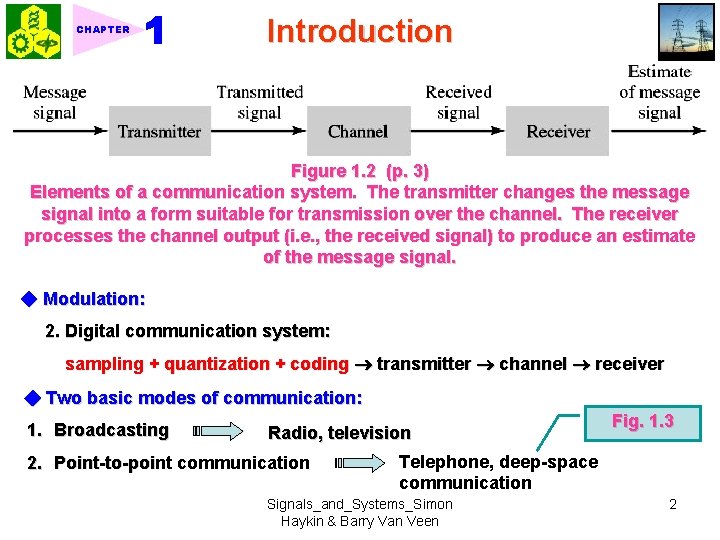
Introduction CHAPTER 1. 1 What is a signal? A signal is formally defined as a function of one or more variables that conveys information on the nature of a physical phenomenon. 1. 2 What is a system? A system is formally defined as an entity that manipulates one or more signals to accomplish a function, thereby yielding new signals. Figure 1. 1 (p. 2) Block diagram representation of a system. 1. 3 Overview of Specific Systems ★ 1. 3. 1 Communication systems Elements of a communication system Fig. 1. 2 1. Analog communication system: modulator + channel + demodulator Signals_and_Systems_Simon Haykin & Barry Van Veen

CHAPTER Introduction Figure 1. 2 (p. 3) Elements of a communication system. The transmitter changes the message signal into a form suitable for transmission over the channel. The receiver processes the channel output (i. e. , the received signal) to produce an estimate of the message signal. ◆ Modulation: 2. Digital communication system: sampling + quantization + coding transmitter channel receiver ◆ Two basic modes of communication: 1. Broadcasting Radio, television 2. Point-to-point communication Fig. 1. 3 Telephone, deep-space communication Signals_and_Systems_Simon Haykin & Barry Van Veen 2

CHAPTER Introduction Figure 1. 3 (p. 5) (a) Snapshot of Pathfinder exploring the surface of Mars. (b) The 70 -meter (230 -foot) diameter antenna located at Canberra, Australia. The surface of the 70 -meter reflector must remain accurate within a fraction of the signal’s wavelength. (Courtesy of Jet Propulsion Laboratory. ) Signals_and_Systems_Simon Haykin & Barry Van Veen 3

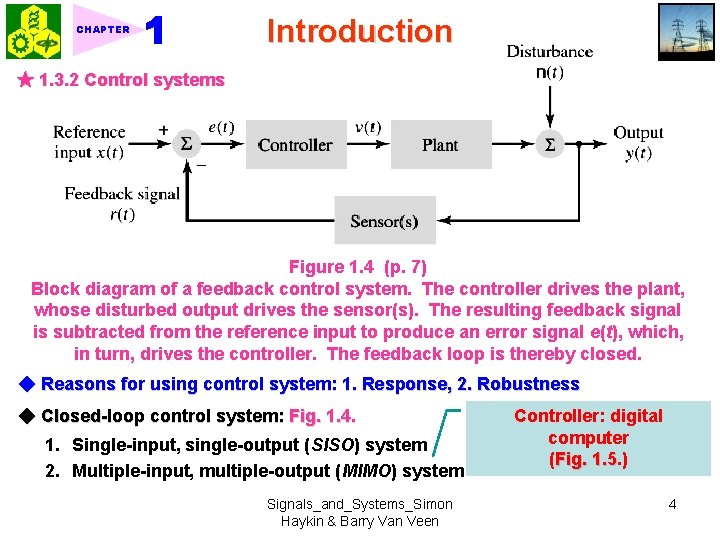
CHAPTER Introduction ★ 1. 3. 2 Control systems Figure 1. 4 (p. 7) Block diagram of a feedback control system. The controller drives the plant, whose disturbed output drives the sensor(s). The resulting feedback signal is subtracted from the reference input to produce an error signal e(t), which, in turn, drives the controller. The feedback loop is thereby closed. ◆ Reasons for using control system: 1. Response, 2. Robustness ◆ Closed-loop control system: Fig. 1. 4. 1. Single-input, single-output (SISO) system 2. Multiple-input, multiple-output (MIMO) system Signals_and_Systems_Simon Haykin & Barry Van Veen Controller: digital computer (Fig. 1. 5. ) 1. 5 4

CHAPTER Introduction Figure 1. 5 (p. 8) NASA space shuttle launch. (Courtesy of NASA. ) Signals_and_Systems_Simon Haykin & Barry Van Veen 5

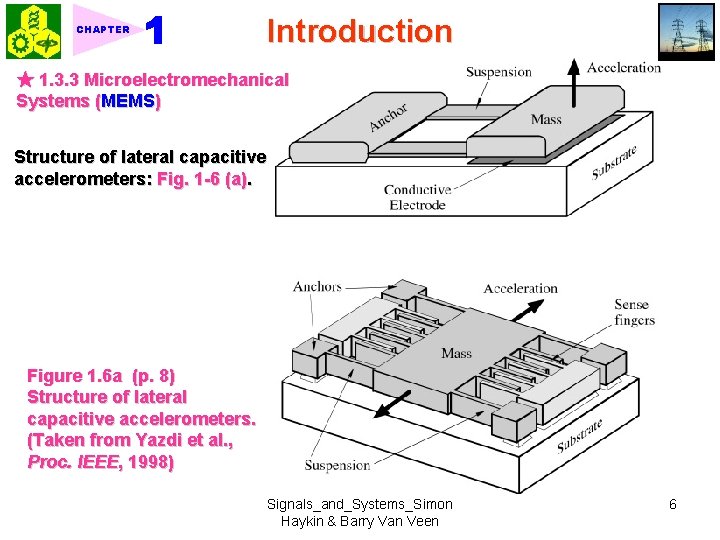
CHAPTER Introduction ★ 1. 3. 3 Microelectromechanical Systems (MEMS) Structure of lateral capacitive accelerometers: Fig. 1 -6 (a). Figure 1. 6 a (p. 8) Structure of lateral capacitive accelerometers. (Taken from Yazdi et al. , Proc. IEEE, 1998) Signals_and_Systems_Simon Haykin & Barry Van Veen 6

CHAPTER Introduction SEM view of Analog Device’s ADXLO 5 surfacemicromachined polysilicon accelerometer: Fig. 1 -6 (b). Figure 1. 6 b (p. 9) SEM view of Analog Device’s ADXLO 5 surfacemicromachined polysilicon accelerometer. (Taken from Yazdi et al. , Proc. IEEE, 1998) Signals_and_Systems_Simon Haykin & Barry Van Veen 7

CHAPTER Introduction ★ 1. 3. 4 Remote Sensing Remote sensing is defined as the process of acquiring information about an object of interest without being in physical contact with it 1. Acquisition of information = detecting and measuring the changes that the object imposes on the field surrounding it. 2. Types of remote sensor: Radar sensor Infrared sensor Visible and near-infrared sensor X-ray sensor ※ Synthetic-aperture radar (SAR) Satisfactory operation High resolution See Fig. 1. 7 Ex. A stereo pair of SAR acquired from earth orbit with Shuttle Imaging Radar (SIR-B) Signals_and_Systems_Simon Haykin & Barry Van Veen 8

CHAPTER Introduction Figure 1. 7 (p. 11) Perspectival view of Mount Shasta (California), derived from a pair of stereo radar images acquired from orbit with the shuttle Imaging Radar (SIR-B). (Courtesy of Jet Propulsion Laboratory. ) Signals_and_Systems_Simon Haykin & Barry Van Veen 9

CHAPTER Introduction ★ 1. 3. 5 Biomedical Signal Processing Morphological types of nerve cells: Fig. 1 -8. Figure 1. 8 (p. 12) Morphological types of nerve cells (neurons) identifiable in monkey cerebral cortex, based on studies of primary somatic sensory and motor cortices. (Reproduced from E. R. Kande, J. H. Schwartz, and T. M. Jessel, Principles of Neural Science, 3 d ed. , 1991; courtesy of Appleton and Lange. ) Signals_and_Systems_Simon Haykin & Barry Van Veen 10

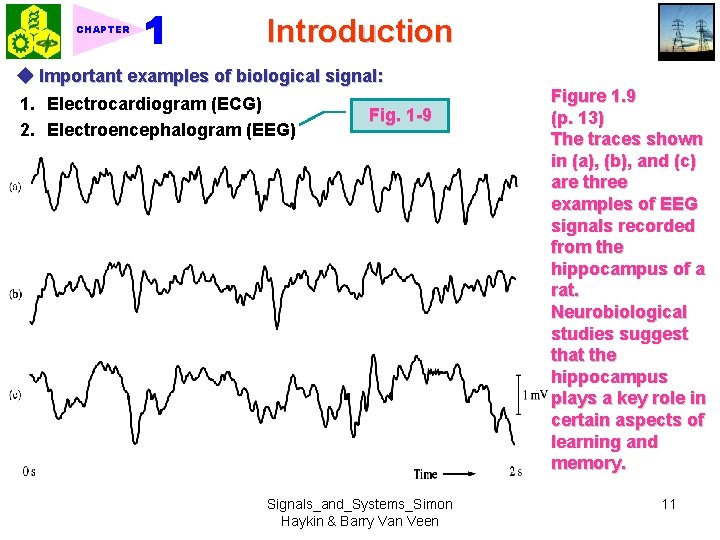
CHAPTER Introduction ◆ Important examples of biological signal: 1. Electrocardiogram (ECG) 2. Electroencephalogram (EEG) Fig. 1 -9 Signals_and_Systems_Simon Haykin & Barry Van Veen Figure 1. 9 (p. 13) The traces shown in (a), (b), and (c) are three examples of EEG signals recorded from the hippocampus of a rat. Neurobiological studies suggest that the hippocampus plays a key role in certain aspects of learning and memory. 11

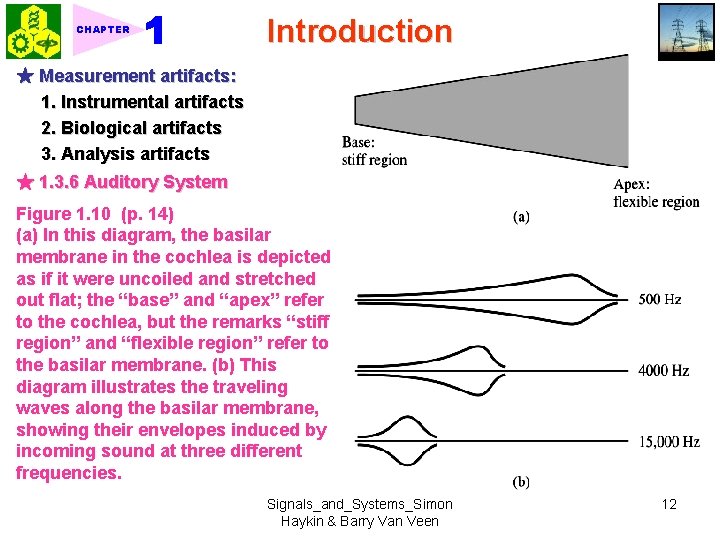
CHAPTER Introduction ★ Measurement artifacts: 1. Instrumental artifacts 2. Biological artifacts 3. Analysis artifacts ★ 1. 3. 6 Auditory System Figure 1. 10 (p. 14) (a) In this diagram, the basilar membrane in the cochlea is depicted as if it were uncoiled and stretched out flat; the “base” and “apex” refer to the cochlea, but the remarks “stiff region” and “flexible region” refer to the basilar membrane. (b) This diagram illustrates the traveling waves along the basilar membrane, showing their envelopes induced by incoming sound at three different frequencies. Signals_and_Systems_Simon Haykin & Barry Van Veen 12

CHAPTER Introduction ★ The ear has three main parts: 1. Outer ear: collection of sound 2. Middle ear: acoustic impedance match between the air and cochlear fluid Conveying the variations of the tympanic membrane (eardrum) 3. Inner ear: mechanical variations → electrochemical or neural signal ★ Basilar membrane: Traveling wave Fig. 1 -10. ★ 1. 3. 7 Analog Versus Digital Signal Processing Digital approach has two advantages over analog approach: 1. Flexibility 2. Repeatability 1. 4 Classification of Signals 1. Continuous-time and discrete-time signals Continuous-time signals: x(t) Parentheses (‧) Fig. 1 -11. (1. 1) where t = n. Ts Discrete-time signals: Fig. 1 -12. Signals_and_Systems_Simon Haykin & Barry Van Veen Brackets [‧] 13

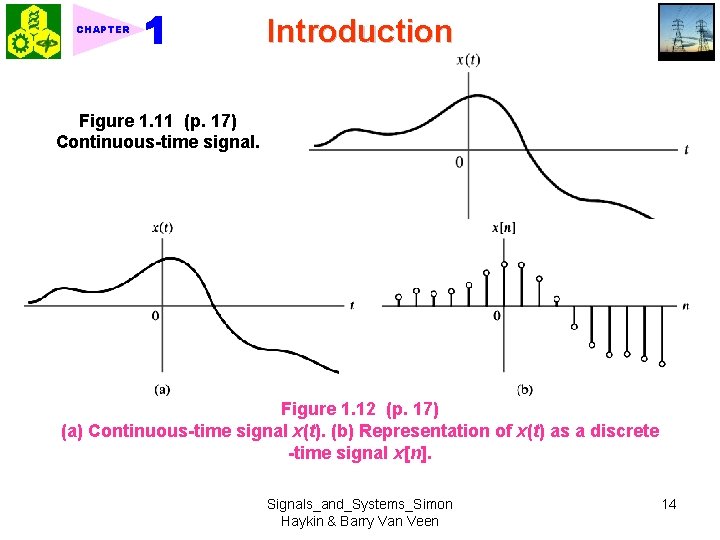
CHAPTER Introduction Figure 1. 11 (p. 17) Continuous-time signal. Figure 1. 12 (p. 17) (a) Continuous-time signal x(t). (b) Representation of x(t) as a discrete -time signal x[n]. Signals_and_Systems_Simon Haykin & Barry Van Veen 14

CHAPTER 2. Even and odd signals Introduction Symmetric about vertical axis Even signals: (1. 2) Odd signals: (1. 3) Example 1. 1 Consider the signal Antisymmetric about origin Is the signal x(t) an even or an odd function of time? <Sol. > odd function Signals_and_Systems_Simon Haykin & Barry Van Veen 15

CHAPTER Introduction ◆ Even-odd decomposition of x(t): where Example 1. 2 Find the even and odd components of the signal <Sol. > (1. 4) Even component: (1. 5) Odd component: Signals_and_Systems_Simon Haykin & Barry Van Veen 16

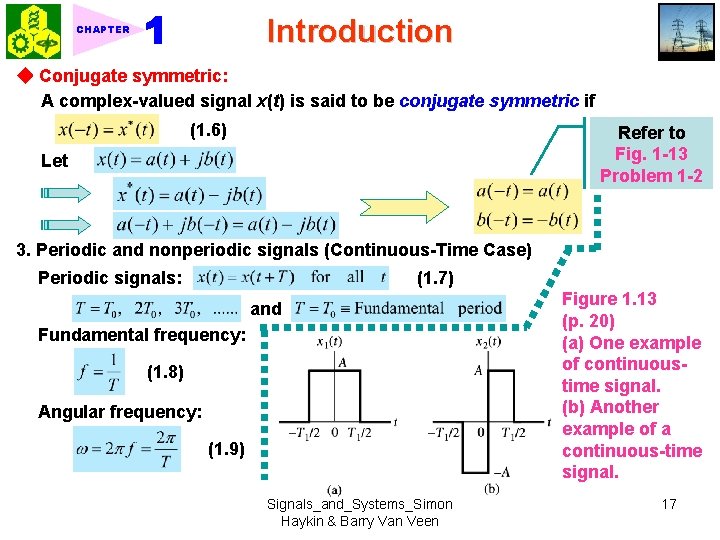
Introduction CHAPTER ◆ Conjugate symmetric: A complex-valued signal x(t) is said to be conjugate symmetric if (1. 6) Refer to Fig. 1 -13 Problem 1 -2 Let 3. Periodic and nonperiodic signals (Continuous-Time Case) (1. 7) Periodic signals: and Fundamental frequency: (1. 8) Angular frequency: (1. 9) Signals_and_Systems_Simon Haykin & Barry Van Veen Figure 1. 13 (p. 20) (a) One example of continuoustime signal. (b) Another example of a continuous-time signal. 17

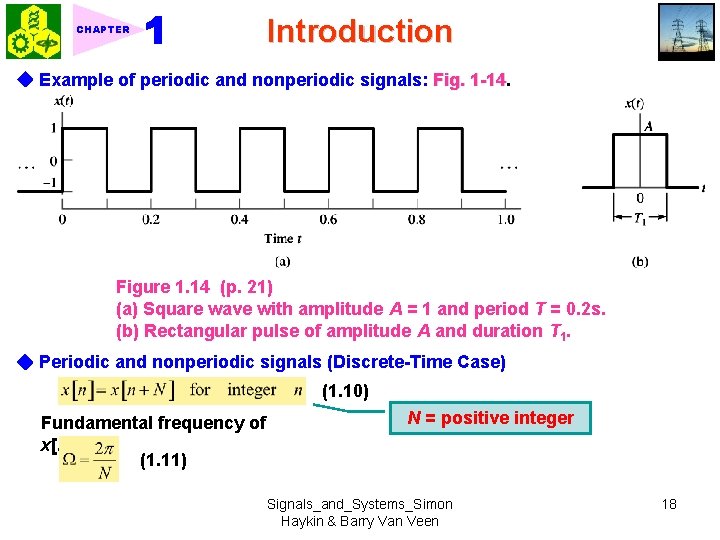
CHAPTER Introduction ◆ Example of periodic and nonperiodic signals: Fig. 1 -14 Figure 1. 14 (p. 21) (a) Square wave with amplitude A = 1 and period T = 0. 2 s. (b) Rectangular pulse of amplitude A and duration T 1. ◆ Periodic and nonperiodic signals (Discrete-Time Case) (1. 10) Fundamental frequency of x[n]: (1. 11) N = positive integer Signals_and_Systems_Simon Haykin & Barry Van Veen 18

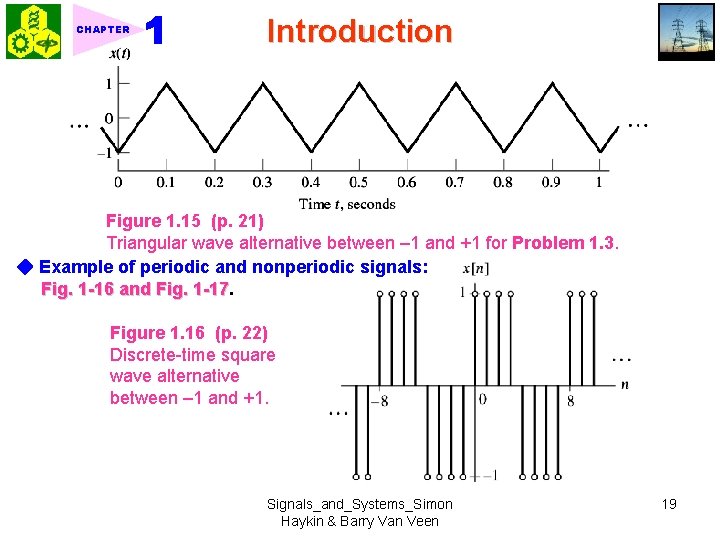
CHAPTER Introduction Figure 1. 15 (p. 21) Triangular wave alternative between – 1 and +1 for Problem 1. 3. ◆ Example of periodic and nonperiodic signals: Fig. 1 -16 and Fig. 1 -17 Figure 1. 16 (p. 22) Discrete-time square wave alternative between – 1 and +1. Signals_and_Systems_Simon Haykin & Barry Van Veen 19

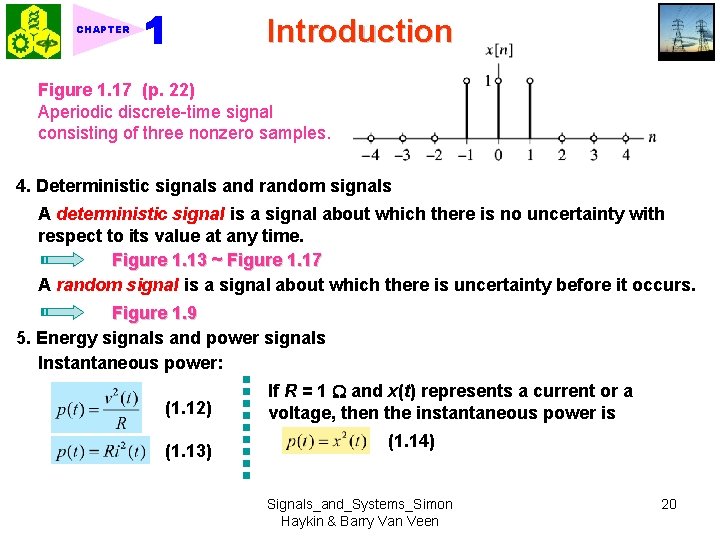
Introduction CHAPTER Figure 1. 17 (p. 22) Aperiodic discrete-time signal consisting of three nonzero samples. 4. Deterministic signals and random signals A deterministic signal is a signal about which there is no uncertainty with respect to its value at any time. Figure 1. 13 ~ Figure 1. 17 A random signal is a signal about which there is uncertainty before it occurs. Figure 1. 9 5. Energy signals and power signals Instantaneous power: (1. 12) (1. 13) If R = 1 and x(t) represents a current or a voltage, then the instantaneous power is (1. 14) Signals_and_Systems_Simon Haykin & Barry Van Veen 20

Introduction CHAPTER The total energy of the continuous-time signal x(t) is (1. 15) ◆ Discrete-time case: Total energy of x[n]: (1. 18) Time-averaged, or average, power is (1. 16) Average power of x[n]: For periodic signal, the time-averaged power is (1. 19) (1. 17) ★ Energy signal: If and only if the total energy of the signal satisfies the condition (1. 20) ★ Power signal: If and only if the average power of the signal satisfies the condition Signals_and_Systems_Simon Haykin & Barry Van Veen 21

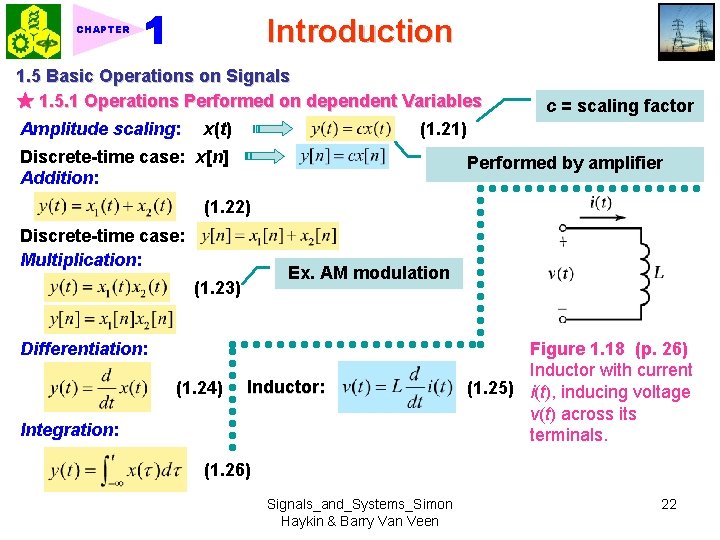
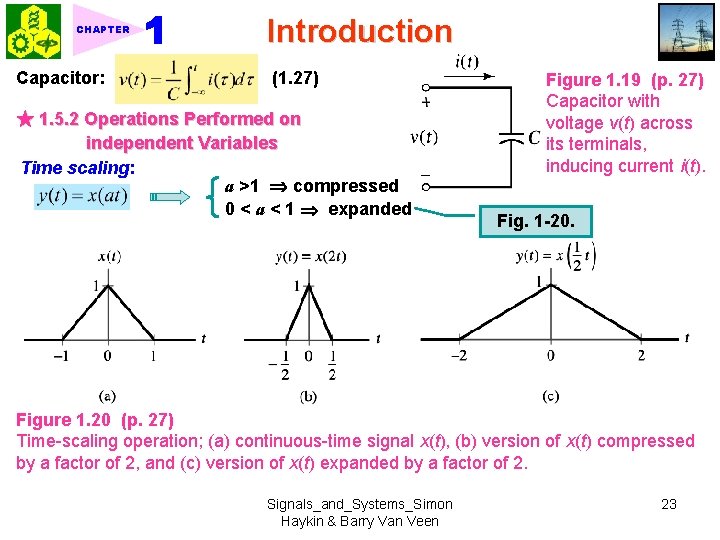
Introduction CHAPTER 1. 5 Basic Operations on Signals ★ 1. 5. 1 Operations Performed on dependent Variables Amplitude scaling: x(t) c = scaling factor (1. 21) Discrete-time case: x[n] Addition: Performed by amplifier (1. 22) Discrete-time case: Multiplication: Ex. AM modulation (1. 23) Differentiation: (1. 24) Inductor: Integration: Figure 1. 18 (p. 26) Inductor with current (1. 25) i(t), inducing voltage v(t) across its terminals. (1. 26) Signals_and_Systems_Simon Haykin & Barry Van Veen 22

CHAPTER Capacitor: Introduction (1. 27) ★ 1. 5. 2 Operations Performed on independent Variables Time scaling: a >1 compressed 0 < a < 1 expanded Figure 1. 19 (p. 27) Capacitor with voltage v(t) across its terminals, inducing current i(t). Fig. 1 -20. Figure 1. 20 (p. 27) Time-scaling operation; (a) continuous-time signal x(t), (b) version of x(t) compressed by a factor of 2, and (c) version of x(t) expanded by a factor of 2. Signals_and_Systems_Simon Haykin & Barry Van Veen 23

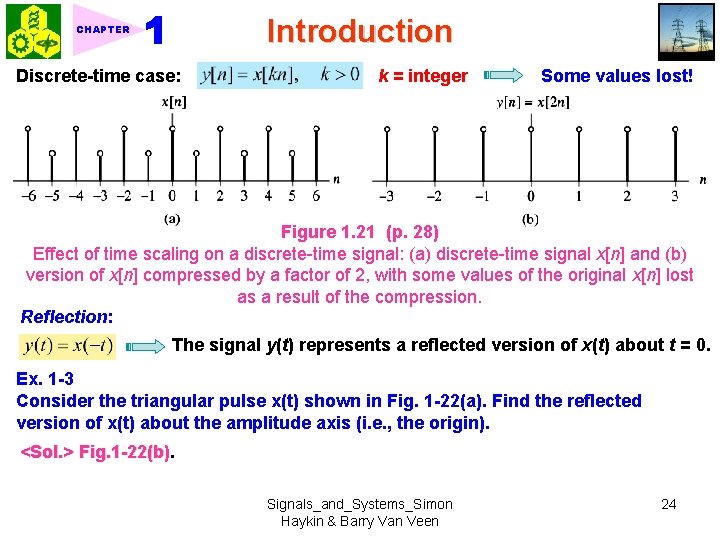
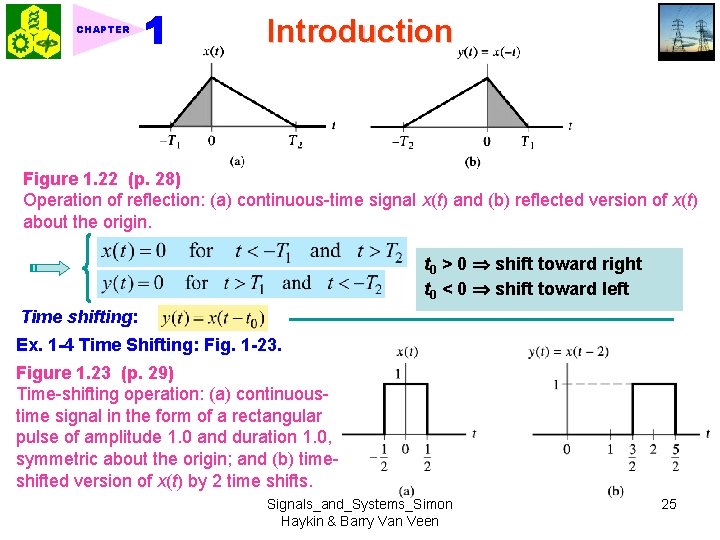
Introduction CHAPTER Discrete-time case: k = integer Some values lost! Figure 1. 21 (p. 28) Effect of time scaling on a discrete-time signal: (a) discrete-time signal x[n] and (b) version of x[n] compressed by a factor of 2, with some values of the original x[n] lost as a result of the compression. Reflection: The signal y(t) represents a reflected version of x(t) about t = 0. Ex. 1 -3 Consider the triangular pulse x(t) shown in Fig. 1 -22(a). Find the reflected version of x(t) about the amplitude axis (i. e. , the origin). <Sol. > Fig. 1 -22(b) Signals_and_Systems_Simon Haykin & Barry Van Veen 24

CHAPTER Introduction Figure 1. 22 (p. 28) Operation of reflection: (a) continuous-time signal x(t) and (b) reflected version of x(t) about the origin. t 0 > 0 shift toward right t 0 < 0 shift toward left Time shifting: Ex. 1 -4 Time Shifting: Fig. 1 -23. Figure 1. 23 (p. 29) Time-shifting operation: (a) continuoustime signal in the form of a rectangular pulse of amplitude 1. 0 and duration 1. 0, symmetric about the origin; and (b) timeshifted version of x(t) by 2 time shifts. Signals_and_Systems_Simon Haykin & Barry Van Veen 25

Introduction CHAPTER Discrete-time case: where m is a positive or negative integer ★ 1. 5. 3 Precedence Rule for Time Shifting and Time Scaling 1. Combination of time shifting and time scaling: (1. 28) (1. 29) (1. 30) 2. Operation order: To achieve Eq. (1. 28), 1 st step: time shifting 2 nd step: time scaling Ex. 1 -5 Precedence Rule for Continuous-Time Signal Consider the rectangular pulse x(t) depicted in Fig. 1 -24(a). Find y(t)=x(2 t + 3). <Sol. > Case 1: Fig. 1 -24. Shifting first, then scaling Case 2: Fig. 1 -25. Scaling first, then shifting Signals_and_Systems_Simon Haykin & Barry Van Veen 26

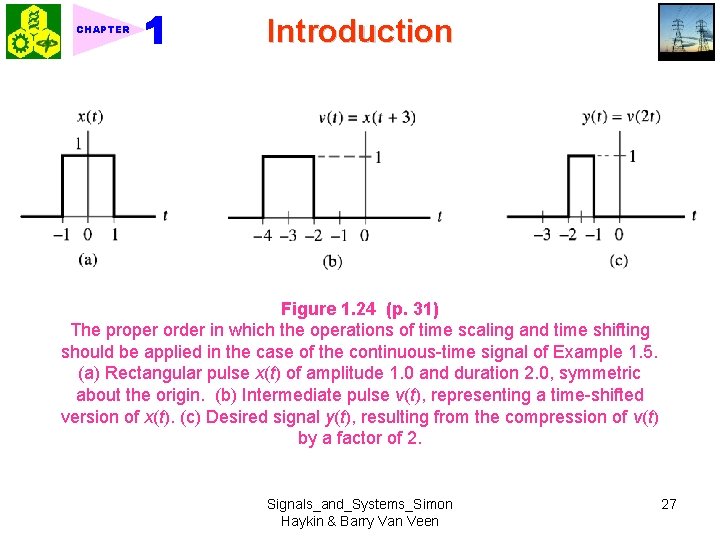
CHAPTER Introduction Figure 1. 24 (p. 31) The proper order in which the operations of time scaling and time shifting should be applied in the case of the continuous-time signal of Example 1. 5. (a) Rectangular pulse x(t) of amplitude 1. 0 and duration 2. 0, symmetric about the origin. (b) Intermediate pulse v(t), representing a time-shifted version of x(t). (c) Desired signal y(t), resulting from the compression of v(t) by a factor of 2. Signals_and_Systems_Simon Haykin & Barry Van Veen 27

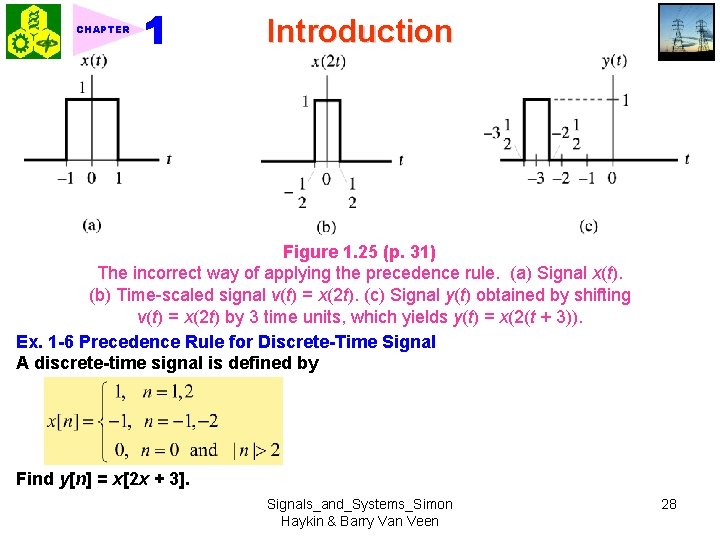
CHAPTER Introduction Figure 1. 25 (p. 31) The incorrect way of applying the precedence rule. (a) Signal x(t). (b) Time-scaled signal v(t) = x(2 t). (c) Signal y(t) obtained by shifting v(t) = x(2 t) by 3 time units, which yields y(t) = x(2(t + 3)). Ex. 1 -6 Precedence Rule for Discrete-Time Signal A discrete-time signal is defined by Find y[n] = x[2 x + 3]. Signals_and_Systems_Simon Haykin & Barry Van Veen 28

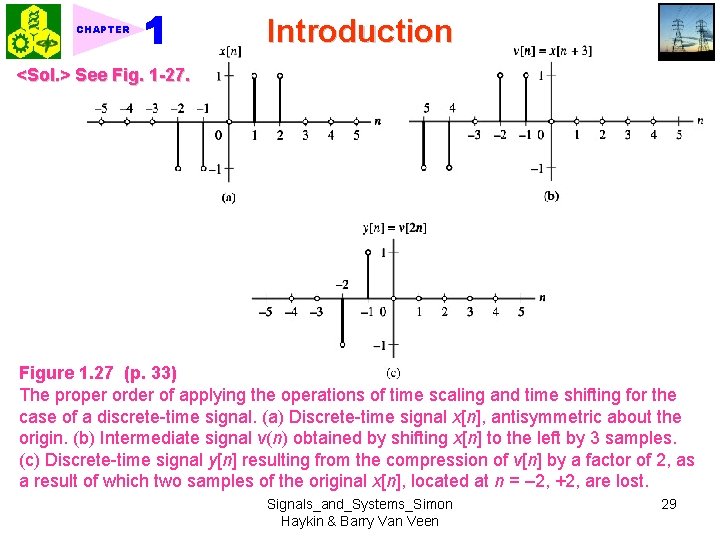
CHAPTER Introduction <Sol. > See Fig. 1 -27. Figure 1. 27 (p. 33) The proper order of applying the operations of time scaling and time shifting for the case of a discrete-time signal. (a) Discrete-time signal x[n], antisymmetric about the origin. (b) Intermediate signal v(n) obtained by shifting x[n] to the left by 3 samples. (c) Discrete-time signal y[n] resulting from the compression of v[n] by a factor of 2, as a result of which two samples of the original x[n], located at n = – 2, +2, are lost. Signals_and_Systems_Simon Haykin & Barry Van Veen 29

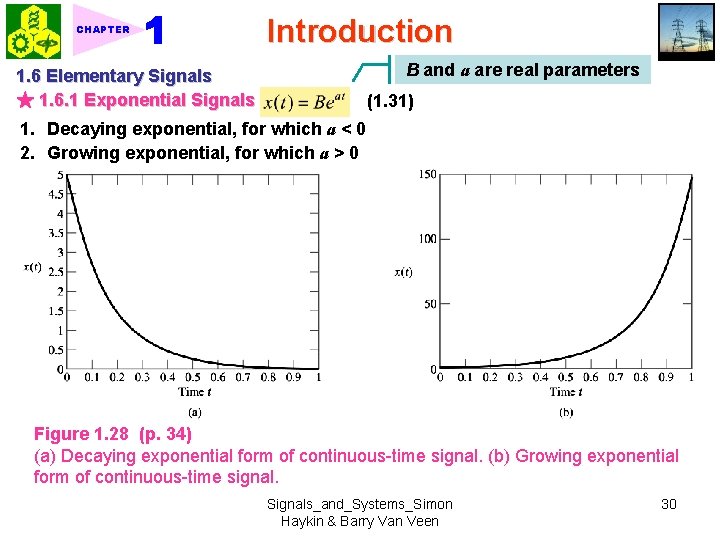
CHAPTER Introduction B and a are real parameters 1. 6 Elementary Signals ★ 1. 6. 1 Exponential Signals (1. 31) 1. Decaying exponential, for which a < 0 2. Growing exponential, for which a > 0 Figure 1. 28 (p. 34) (a) Decaying exponential form of continuous-time signal. (b) Growing exponential form of continuous-time signal. Signals_and_Systems_Simon Haykin & Barry Van Veen 30

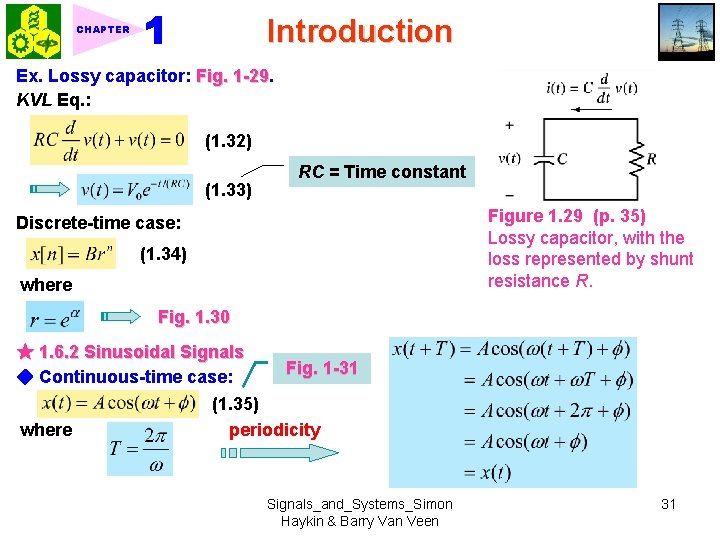
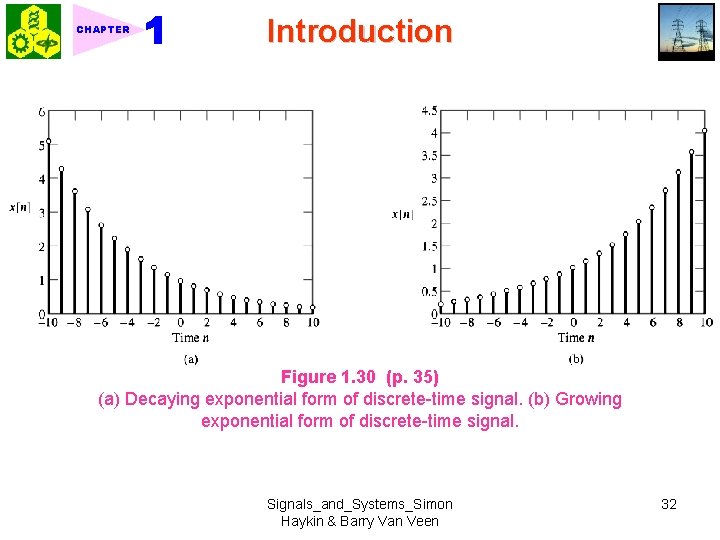
Introduction CHAPTER Ex. Lossy capacitor: Fig. 1 -29 KVL Eq. : (1. 32) (1. 33) RC = Time constant Figure 1. 29 (p. 35) Lossy capacitor, with the loss represented by shunt resistance R. Discrete-time case: (1. 34) where Fig. 1. 30 ★ 1. 6. 2 Sinusoidal Signals ◆ Continuous-time case: where Fig. 1 -31 (1. 35) periodicity Signals_and_Systems_Simon Haykin & Barry Van Veen 31

CHAPTER Introduction Figure 1. 30 (p. 35) (a) Decaying exponential form of discrete-time signal. (b) Growing exponential form of discrete-time signal. Signals_and_Systems_Simon Haykin & Barry Van Veen 32

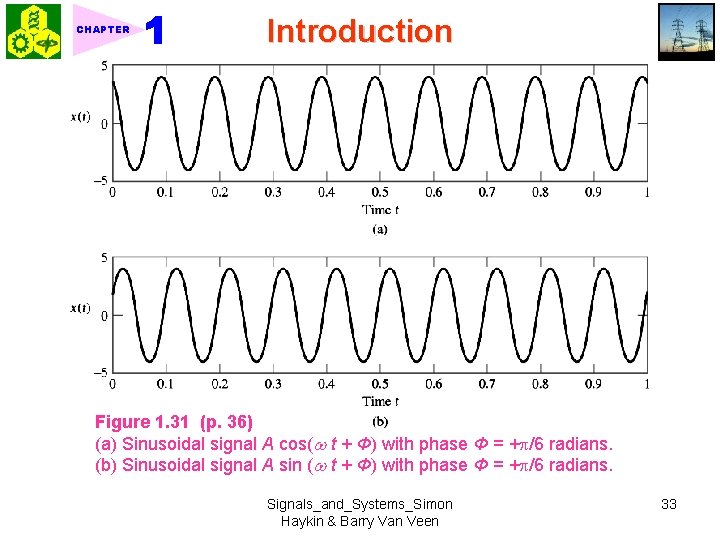
CHAPTER Introduction Figure 1. 31 (p. 36) (a) Sinusoidal signal A cos( t + Φ) with phase Φ = + /6 radians. (b) Sinusoidal signal A sin ( t + Φ) with phase Φ = + /6 radians. Signals_and_Systems_Simon Haykin & Barry Van Veen 33

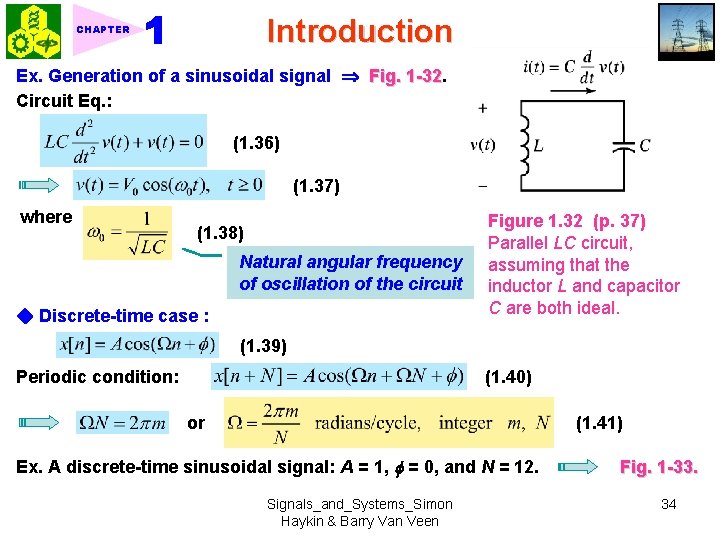
Introduction CHAPTER Ex. Generation of a sinusoidal signal Fig. 1 -32 Circuit Eq. : (1. 36) (1. 37) where (1. 38) Natural angular frequency of oscillation of the circuit ◆ Discrete-time case : Figure 1. 32 (p. 37) Parallel LC circuit, assuming that the inductor L and capacitor C are both ideal. (1. 39) Periodic condition: (1. 40) or (1. 41) Ex. A discrete-time sinusoidal signal: A = 1, = 0, and N = 12. Signals_and_Systems_Simon Haykin & Barry Van Veen Fig. 1 -33. 34

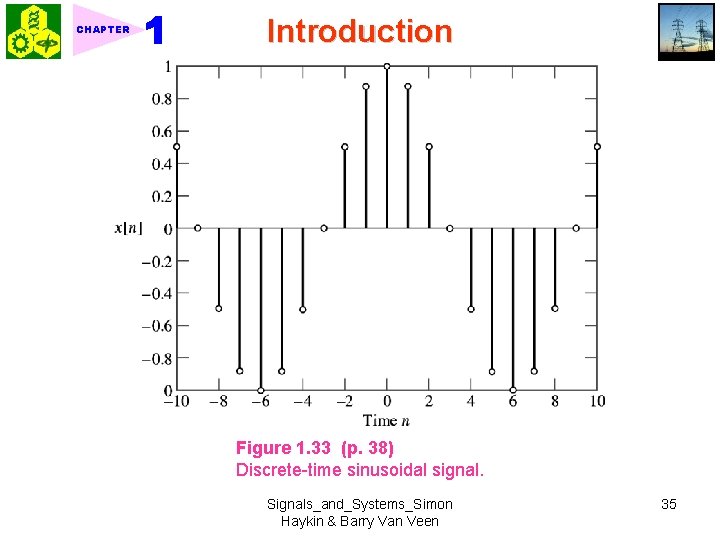
CHAPTER Introduction Figure 1. 33 (p. 38) Discrete-time sinusoidal signal. Signals_and_Systems_Simon Haykin & Barry Van Veen 35

Introduction CHAPTER Example 1. 7 Discrete-Time Sinusoidal Signal A pair of sinusoidal signals with a common angular frequency is defined by and (a) Both x 1[n] and x 2[n] are periodic. Find their common fundamental period. (b) Express the composite sinusoidal signal In the form y[n] = Acos( n + ), and evaluate the amplitude A and phase . <Sol. > (a) Angular frequency of both x 1[n] and x 2[n]: This can be only for m = 5, 10, 15, …, which results in N = 2, 4, 6, … (b) Trigonometric identity: Let = 5 , then compare x 1[n] + x 2[n] with the above equation to obtain that Signals_and_Systems_Simon Haykin & Barry Van Veen 36

Introduction CHAPTER f= /6 Accordingly, we may express y[n] as ★ 1. 6. 3 Relation Between Sinusoidal and Complex Exponential Signals 1. Euler’s identity: Complex exponential signal: (1. 41) (1. 42) (1. 35) (1. 42) Signals_and_Systems_Simon Haykin & Barry Van Veen 37

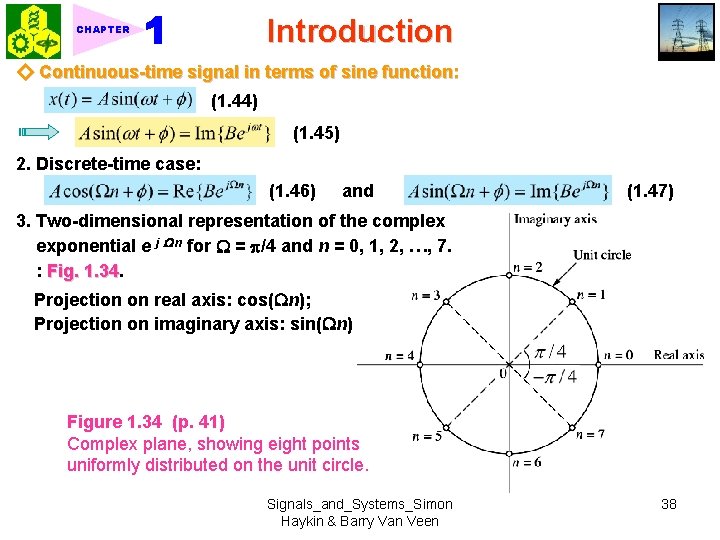
Introduction CHAPTER ◇ Continuous-time signal in terms of sine function: (1. 44) (1. 45) 2. Discrete-time case: (1. 46) and (1. 47) 3. Two-dimensional representation of the complex exponential e j n for = /4 and n = 0, 1, 2, …, 7. : Fig. 1. 34 Projection on real axis: cos( n); Projection on imaginary axis: sin( n) Figure 1. 34 (p. 41) Complex plane, showing eight points uniformly distributed on the unit circle. Signals_and_Systems_Simon Haykin & Barry Van Veen 38

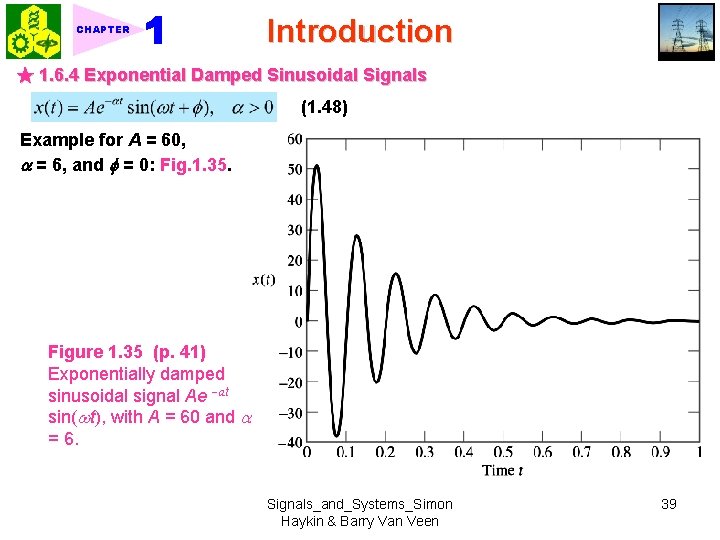
CHAPTER Introduction ★ 1. 6. 4 Exponential Damped Sinusoidal Signals (1. 48) Example for A = 60, = 6, and = 0: Fig. 1. 35 Figure 1. 35 (p. 41) Exponentially damped sinusoidal signal Ae at sin( t), with A = 60 and = 6. Signals_and_Systems_Simon Haykin & Barry Van Veen 39

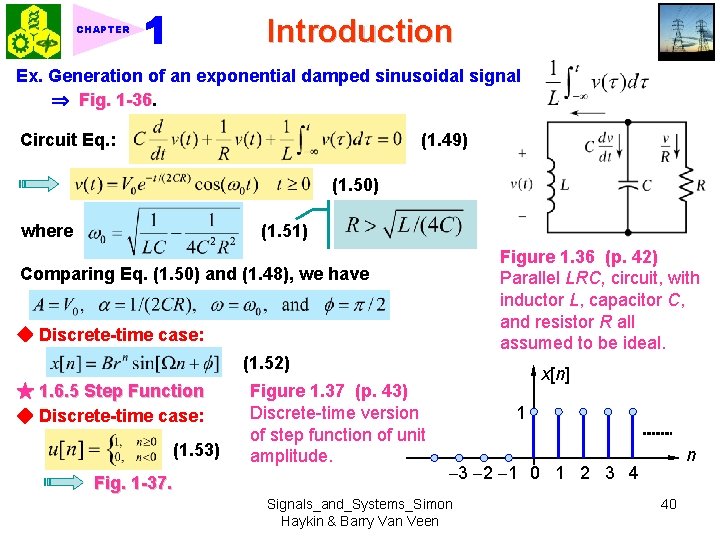
Introduction CHAPTER Ex. Generation of an exponential damped sinusoidal signal Fig. 1 -36 Circuit Eq. : (1. 49) (1. 50) where (1. 51) Figure 1. 36 (p. 42) Parallel LRC, circuit, with inductor L, capacitor C, and resistor R all assumed to be ideal. Comparing Eq. (1. 50) and (1. 48), we have ◆ Discrete-time case: (1. 52) ★ 1. 6. 5 Step Function ◆ Discrete-time case: (1. 53) Fig. 1 -37. Figure 1. 37 (p. 43) Discrete-time version of step function of unit amplitude. x[n] 1 n 3 2 1 0 1 2 3 4 Signals_and_Systems_Simon Haykin & Barry Van Veen 40

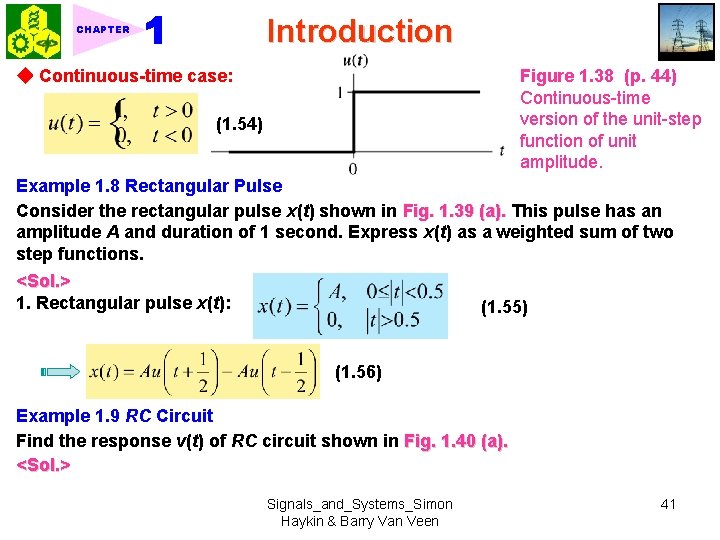
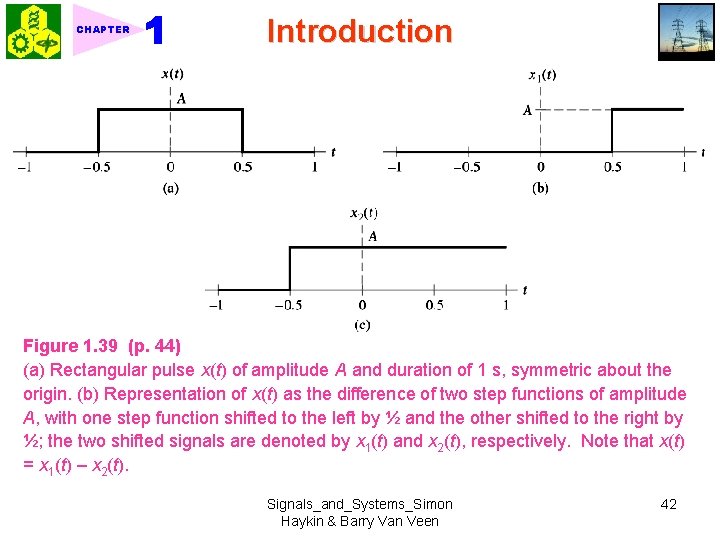
Introduction CHAPTER ◆ Continuous-time case: Figure 1. 38 (p. 44) Continuous-time version of the unit-step function of unit amplitude. (1. 54) Example 1. 8 Rectangular Pulse Consider the rectangular pulse x(t) shown in Fig. 1. 39 (a). This pulse has an amplitude A and duration of 1 second. Express x(t) as a weighted sum of two step functions. <Sol. > 1. Rectangular pulse x(t): (1. 55) (1. 56) Example 1. 9 RC Circuit Find the response v(t) of RC circuit shown in Fig. 1. 40 (a). <Sol. > Signals_and_Systems_Simon Haykin & Barry Van Veen 41

CHAPTER Introduction Figure 1. 39 (p. 44) (a) Rectangular pulse x(t) of amplitude A and duration of 1 s, symmetric about the origin. (b) Representation of x(t) as the difference of two step functions of amplitude A, with one step function shifted to the left by ½ and the other shifted to the right by ½; the two shifted signals are denoted by x 1(t) and x 2(t), respectively. Note that x(t) = x 1(t) – x 2(t). Signals_and_Systems_Simon Haykin & Barry Van Veen 42

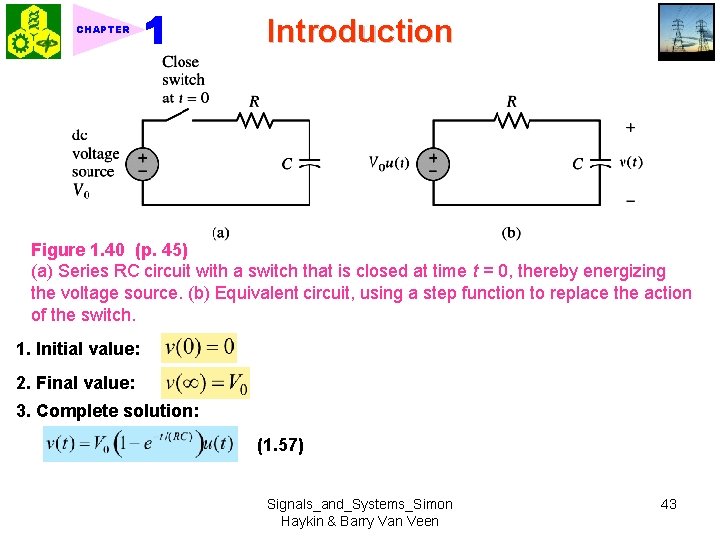
CHAPTER Introduction Figure 1. 40 (p. 45) (a) Series RC circuit with a switch that is closed at time t = 0, thereby energizing the voltage source. (b) Equivalent circuit, using a step function to replace the action of the switch. 1. Initial value: 2. Final value: 3. Complete solution: (1. 57) Signals_and_Systems_Simon Haykin & Barry Van Veen 43

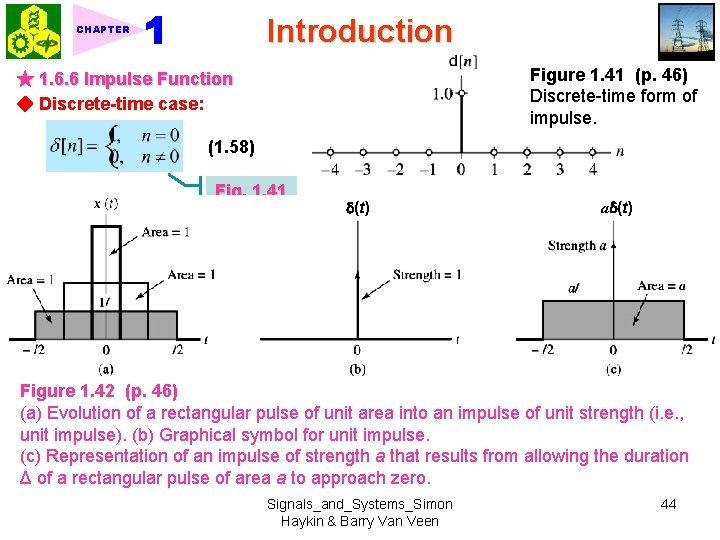
Introduction CHAPTER Figure 1. 41 (p. 46) Discrete-time form of impulse. ★ 1. 6. 6 Impulse Function ◆ Discrete-time case: (1. 58) Fig. 1. 41 (t) a (t) Figure 1. 41 (p. 46) Discrete-time form of impulse. Figure 1. 42 (p. 46) (a) Evolution of a rectangular pulse of unit area into an impulse of unit strength (i. e. , unit impulse). (b) Graphical symbol for unit impulse. (c) Representation of an impulse of strength a that results from allowing the duration Δ of a rectangular pulse of area a to approach zero. Signals_and_Systems_Simon Haykin & Barry Van Veen 44

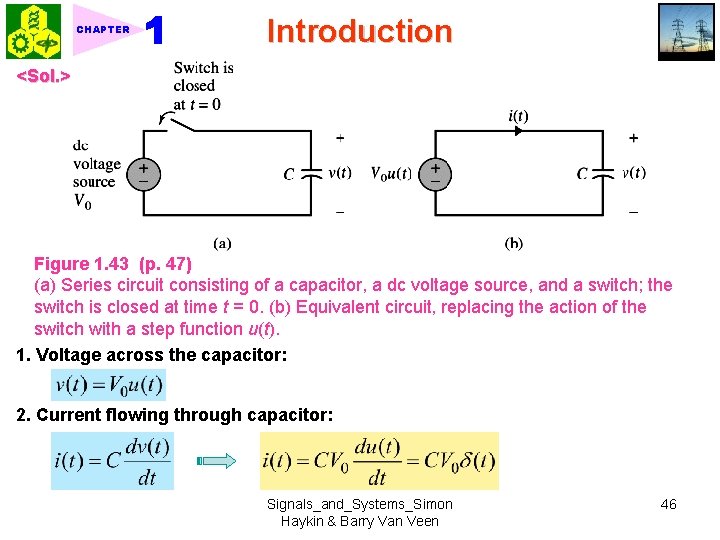
Introduction CHAPTER ◆ Continuous-time case: Dirac delta function (1. 59) (1. 60) 1. As the duration decreases, the rectangular pulse approximates the impulse more closely. Fig. 1. 42. 2. Mathematical relation between impulse and rectangular pulse function: (1. 61) Fig. 1. 42 (a). 3. (t) is the derivative of u(t): 1. x (t): even function of t, = duration. 2. x (t): Unit area. 4. u(t) is the integral of (t): (1. 62) (1. 63) Example 1. 10 RC Circuit (Continued) For the RC circuit shown in Fig. 1. 43 (a), determine the current i (t) that flows through the capacitor for t 0. Signals_and_Systems_Simon Haykin & Barry Van Veen 45

CHAPTER Introduction <Sol. > Figure 1. 43 (p. 47) (a) Series circuit consisting of a capacitor, a dc voltage source, and a switch; the switch is closed at time t = 0. (b) Equivalent circuit, replacing the action of the switch with a step function u(t). 1. Voltage across the capacitor: 2. Current flowing through capacitor: Signals_and_Systems_Simon Haykin & Barry Van Veen 46

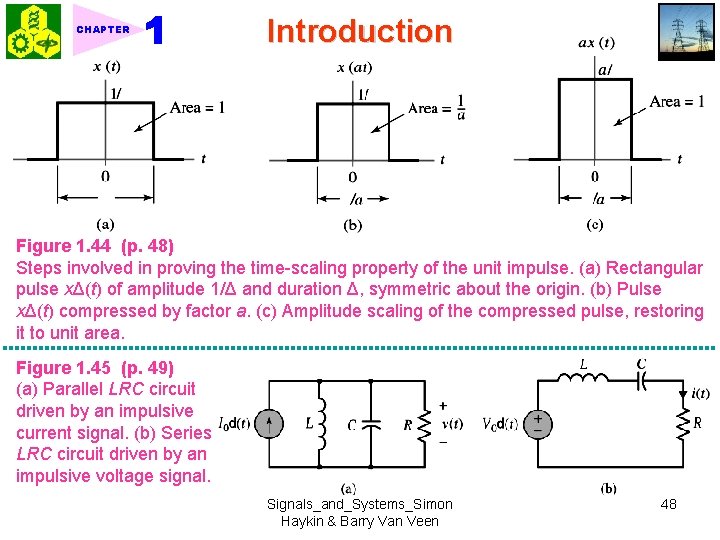
Introduction CHAPTER ◆ Properties of impulse function: 1. Even function: (1. 64) 2. Sifting property: (1. 65) 3. Time-scaling property: (1. 66) (1. 68) Ex. RLC circuit driven by impulsive source: Fig. 1. 45. For Fig. 1. 45 (a), (a) the voltage across the capacitor at time t = 0+ is (1. 69) <p. f. > Fig. 1. 44 1. Rectangular pulse approximation: (1. 67) 2. Unit area pulse: Fig. 1. 44(a). Time scaling: Fig. 1. 44(b). Area = 1/a ax (at) Restoring unit area Signals_and_Systems_Simon Haykin & Barry Van Veen 47

CHAPTER Introduction Figure 1. 44 (p. 48) Steps involved in proving the time-scaling property of the unit impulse. (a) Rectangular pulse xΔ(t) of amplitude 1/Δ and duration Δ, symmetric about the origin. (b) Pulse xΔ(t) compressed by factor a. (c) Amplitude scaling of the compressed pulse, restoring it to unit area. Figure 1. 45 (p. 49) (a) Parallel LRC circuit driven by an impulsive current signal. (b) Series LRC circuit driven by an impulsive voltage signal. Signals_and_Systems_Simon Haykin & Barry Van Veen 48

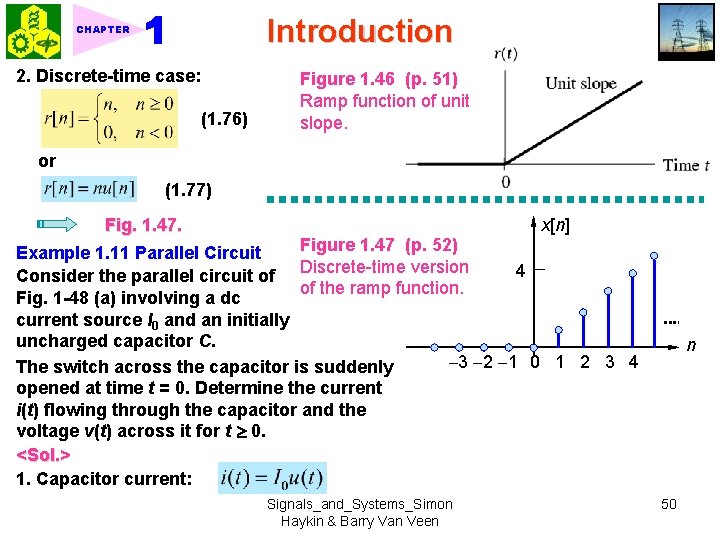
Introduction CHAPTER ★ 1. 6. 7 Derivatives of The Impulse 1. Doublet: Problem 1. 24 (1. 70) 2. Fundamental property of the doublet: (1. 71) (1. 72) 3. Second derivative of impulse: (1. 73) ★ 1. 6. 8 Ramp Function 1. Continuous-time case: (1. 74) or (1. 75) Signals_and_Systems_Simon Haykin & Barry Van Veen Fig. 1. 46 49

Introduction CHAPTER 2. Discrete-time case: (1. 76) Figure 1. 46 (p. 51) Ramp function of unit slope. or (1. 77) x[n] Fig. 1. 47. Figure 1. 47 (p. 52) Example 1. 11 Parallel Circuit Discrete-time version 4 Consider the parallel circuit of of the ramp function. Fig. 1 -48 (a) involving a dc current source I 0 and an initially uncharged capacitor C. 3 2 1 0 1 2 3 4 The switch across the capacitor is suddenly opened at time t = 0. Determine the current i(t) flowing through the capacitor and the voltage v(t) across it for t 0. <Sol. > 1. Capacitor current: Signals_and_Systems_Simon Haykin & Barry Van Veen n 50

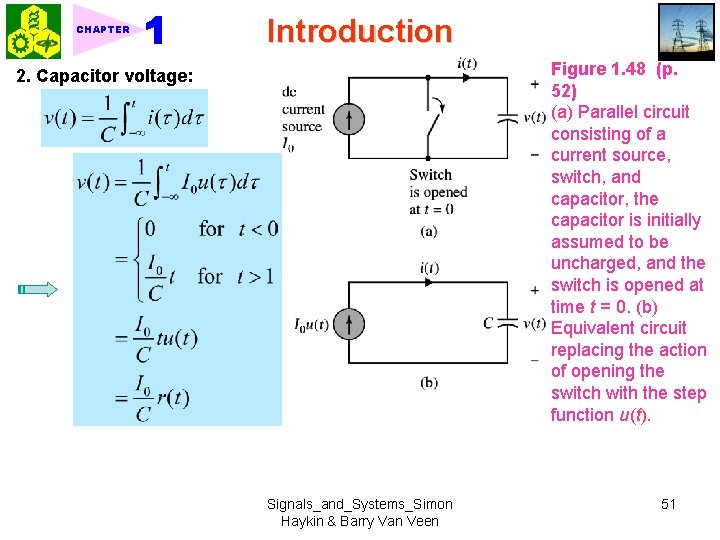
CHAPTER Introduction Figure 1. 48 (p. 52) (a) Parallel circuit consisting of a current source, switch, and capacitor, the capacitor is initially assumed to be uncharged, and the switch is opened at time t = 0. (b) Equivalent circuit replacing the action of opening the switch with the step function u(t). 2. Capacitor voltage: Signals_and_Systems_Simon Haykin & Barry Van Veen 51

Introduction CHAPTER 1. 7 Systems Viewed as Interconnections of Operations A system may be viewed as an interconnection of operations that transforms an input signal into an output signal with properties different from those of the input signal. 1. Continuous-time case: (1. 78) 2. Discrete-time case: (1. 79) Fig. 1 -49 (a) and (b). Figure 1. 49 (p. 53) Block diagram representation of operator H for (a) continuous time and (b) discrete time. Example 1. 12 Moving-average system Consider a discrete-time system whose output signal y[n] is the average of the three most recent values of the input signal x[n], that is Formulate the operator H for this system; hence, develop a block diagram representation for it. Signals_and_Systems_Simon Haykin & Barry Van Veen 52

CHAPTER Introduction <Sol. > 1. Discrete-time-shift operator Sk: Fig. 1. 50 Shifts the input x[n] by k time units to produce an output equal to x[n k]. 2. Overall operator H for the moving-average system: Fig. 1 -51. Figure 1. 50 (p. 54) Discrete-time-shift operator Sk, operating on the discretetime signal x[n] to produce x[n – k]. Fig. 1 -51 (a): cascade form; Fig. 1 -51 (b): parallel form. 1. 8 Properties of Systems ★ 1. 8. 1 Stability 1. A system is said to be bounded-input, bounded-output (BIBO) BIBO stable if and only if every bounded input results in a bounded output. 2. The operator H is BIBO stable if the output signal y(t) satisfies the condition (1. 80) whenever the input signals x(t) satisfy the condition (1. 81) Signals_and_Systems_Simon Haykin & Barry Van Veen Both Mx and My represent some finite positive number 53

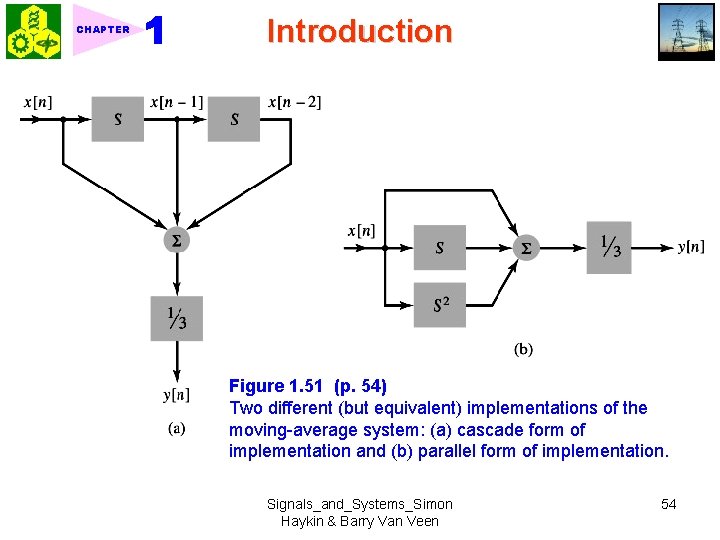
CHAPTER Introduction Figure 1. 51 (p. 54) Two different (but equivalent) implementations of the moving-average system: (a) cascade form of implementation and (b) parallel form of implementation. Signals_and_Systems_Simon Haykin & Barry Van Veen 54

CHAPTER Introduction One famous example of an unstable system: Figure 1. 52 a (p. 56) Dramatic photographs showing the collapse of the Tacoma Narrows suspension bridge on November 7, 1940. (a) Photograph showing the twisting motion of the bridge’s center span just before failure. (b) A few minutes after the first piece of concrete fell, this second photograph shows a 600 -ft section of the bridge breaking out of the suspension span and turning upside down as it crashed in Puget Sound, Washington. Note the car in the top right-hand corner of the photograph. (Courtesy of the Smithsonian Institution. ) Signals_and_Systems_Simon Haykin & Barry Van Veen 55

CHAPTER Introduction Example 1. 13 Moving-average system (continued) Show that the moving-average system described in Example 1. 12 is BIBO stable. <p. f. > 1. Assume that: 2. Input-output relation: The moving-average system is stable. Signals_and_Systems_Simon Haykin & Barry Van Veen 56

CHAPTER Introduction Example 1. 14 Unstable system Consider a discrete-time system whose input-output relation is defined by where r > 1. Show that this system is unstable. <p. f. > 1. Assume that: 2. We find that With r > 1, the multiplying factor rn diverges for increasing n. The system is unstable. ★ 1. 8. 2 Memory A system is said to possess memory if its output signal depends on past or future values of the input signal. A system is said to possess memoryless if its output signal depends only on the present values of the input signal. Signals_and_Systems_Simon Haykin & Barry Van Veen 57

Introduction CHAPTER Ex. : Resistor Memoryless ! Ex. : Inductor Memory ! Ex. : Moving-average system Memory ! Ex. : A system described by the input-output relation Memoryless ! ★ 1. 8. 3 Causality A system is said to be causal if its present value of the output signal depends only on the present or past values of the input signal. A system is said to be noncausal if its output signal depends on one or more future values of the input signal. Signals_and_Systems_Simon Haykin & Barry Van Veen 58

CHAPTER Introduction Ex. : Moving-average system Causal ! Ex. : Moving-average system Noncausal ! A causal system must be capable of operating in real time ★ 1. 8. 4 Invertibility A system is said to be invertible if the input of the system can be recovered from the output. 1. Continuous-time system: Fig. 1. 54 x(t) = input; y(t) = output H = first system operator; H inv = second system operator Figure 1. 54 (p. 59) The notion of system invertibility. The second operator H inv is the inverse of the first operator H. Hence, the input x(t) is passed through the cascade correction of H and H inv completely unchanged. Signals_and_Systems_Simon Haykin & Barry Van Veen 59

Introduction CHAPTER 2. Output of the second system: H inv = inverse operator 3. Condition for invertible system: (1. 82) I = identity operator Example 1. 15 Inverse of System Consider the time-shift system described by the input-output relation where the operator S t 0 represents a time shift of t 0 seconds. Find the inverse of this system. <Sol. > 1. Inverse operator S t 0: 2. Invertibility condition: Time shift of t 0 Signals_and_Systems_Simon Haykin & Barry Van Veen 60

CHAPTER Introduction Example 1. 16 Non-Invertible System Show that a square-law system described by the input-output relation is not invertible. <p. f. > Since the distinct inputs x(t) and x(t) produce the same output y(t). Accordingly, the square-law system is not invertible. ★ 1. 8. 5 Time Invariance A system is said to be time invariance if a time delay or time advance of the input signal leads to an identical time shift in the output signal. A time-invariant system do not change with time. Figure 1. 55 (p. 61) The notion of time invariance. (a) Time-shift operator St 0 preceding operator H. (b) Time-shift operator St 0 following operator H. These two situations are equivalent, provided that H is time invariant. Signals_and_Systems_Simon Haykin & Barry Van Veen 61

Introduction CHAPTER 1. Continuous-time system: 2. Input signal x 1(t) is shifted in time by t 0 seconds: S t 0 = operator of a time shift equal to t 0 3. Output of system H: (1. 83) 4. For Fig. 1 -55 (b), the output of system H is y 1(t t 0): (1. 84) 5. Condition for time-invariant system: Signals_and_Systems_Simon Haykin & Barry Van Veen (1. 85) 62

CHAPTER Introduction Example 1. 17 Inductor The inductor shown in figure is described by the input-output relation: y 1(t) = i(t) x 1(t) = v(t) where L is the inductance. Show that the inductor so described is time invariant. <Sol. > 1. Let x 1(t) x 1(t t 0) Response y 2(t) of the inductor to x 1(t t 0) is (A) 2. Let y 1(t t 0) = the original output of the inductor, shifted by t 0 seconds: (B) 3. Changing variables: (A) Inductor is time invariant. Signals_and_Systems_Simon Haykin & Barry Van Veen 63

CHAPTER Introduction Example 1. 18 Thermistor Let R(t) denote the resistance of thermistor, expressed as a function of time. We may express the input-output relation of the device as y 1(t) = i(t) x 1(t) = v(t) Show that thermistor so described is time variant. <Sol. > 1. Let response y 2(t) of thermistor to x 1(t t 0) is 2. Let y 1(t t 0) = the original output of thermistor due to x 1(t), shifted by t 0 seconds: 3. Since R(t) R(t t 0) Time variant! Signals_and_Systems_Simon Haykin & Barry Van Veen 64

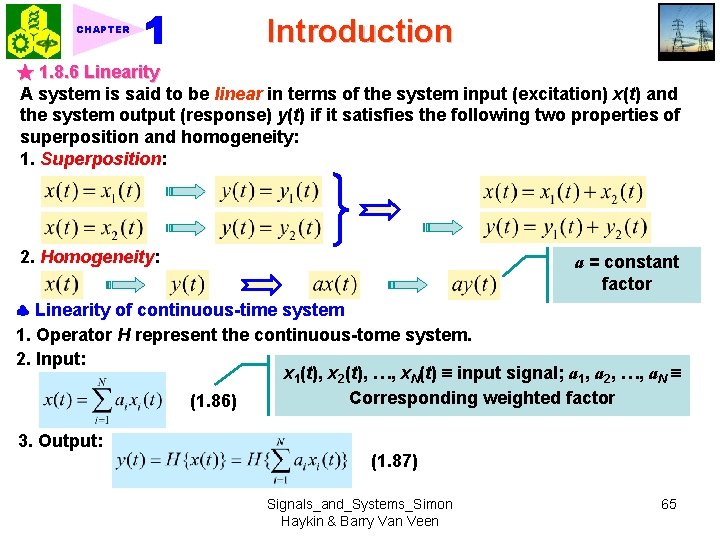
CHAPTER Introduction ★ 1. 8. 6 Linearity A system is said to be linear in terms of the system input (excitation) x(t) and the system output (response) y(t) if it satisfies the following two properties of superposition and homogeneity: 1. Superposition: 2. Homogeneity: a = constant factor Linearity of continuous-time system 1. Operator H represent the continuous-tome system. 2. Input: x 1(t), x 2(t), …, x. N(t) input signal; a 1, a 2, …, a. N Corresponding weighted factor (1. 86) 3. Output: (1. 87) Signals_and_Systems_Simon Haykin & Barry Van Veen 65

CHAPTER Introduction (1. 88) Superposition and homogeneity where (1. 89) 4. Commutation and Linearity: (1. 90) Fig. 1. 56 Linearity of discrete-time system Same results, see Example 1. 19 Linear Discrete-Time system Consider a discrete-time system described by the input-output relation Show that this system is linear. Signals_and_Systems_Simon Haykin & Barry Van Veen 66

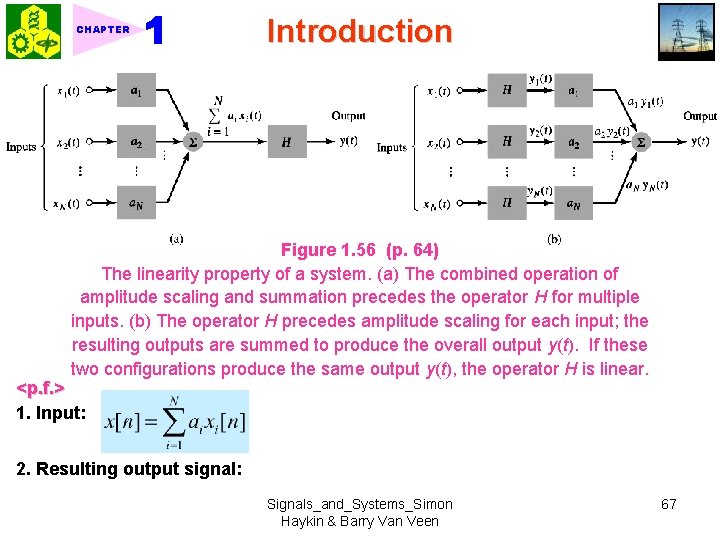
CHAPTER Introduction Figure 1. 56 (p. 64) The linearity property of a system. (a) The combined operation of amplitude scaling and summation precedes the operator H for multiple inputs. (b) The operator H precedes amplitude scaling for each input; the resulting outputs are summed to produce the overall output y(t). If these two configurations produce the same output y(t), the operator H is linear. <p. f. > 1. Input: 2. Resulting output signal: Signals_and_Systems_Simon Haykin & Barry Van Veen 67

CHAPTER Introduction where Linear system! Example 1. 20 Nonlinear Continuous-Time System Consider a continuous-time system described by the input-output relation Show that this system is nonlinear. <p. f. > 1. Input: 2. Output: Here we cannot write Nonlinear system! Signals_and_Systems_Simon Haykin & Barry Van Veen 68

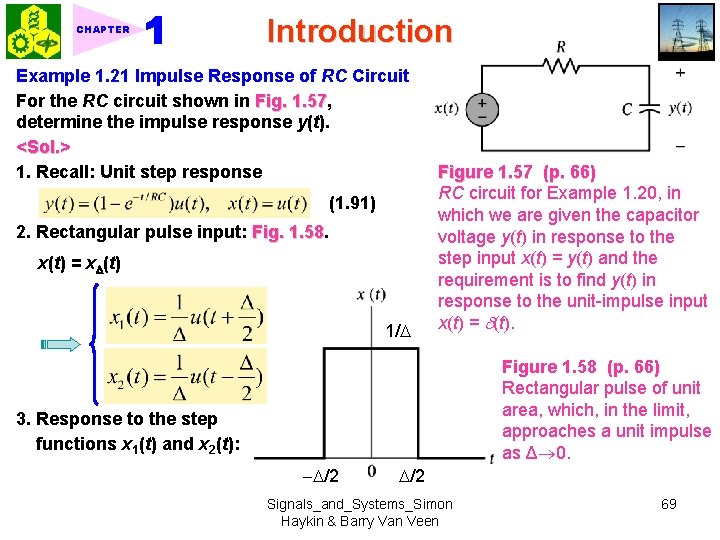
CHAPTER Introduction Example 1. 21 Impulse Response of RC Circuit For the RC circuit shown in Fig. 1. 57, 1. 57 determine the impulse response y(t). <Sol. > 1. Recall: Unit step response (1. 91) 2. Rectangular pulse input: Fig. 1. 58 x(t) = x (t) 1/ Figure 1. 57 (p. 66) RC circuit for Example 1. 20, in which we are given the capacitor voltage y(t) in response to the step input x(t) = y(t) and the requirement is to find y(t) in response to the unit-impulse input x(t) = (t). Figure 1. 58 (p. 66) Rectangular pulse of unit area, which, in the limit, approaches a unit impulse as Δ 0. 3. Response to the step functions x 1(t) and x 2(t): /2 Signals_and_Systems_Simon Haykin & Barry Van Veen 69

CHAPTER Introduction Next, recognizing that i) (t) = the limiting form of the pulse x (t): Signals_and_Systems_Simon Haykin & Barry Van Veen (1. 92) 70

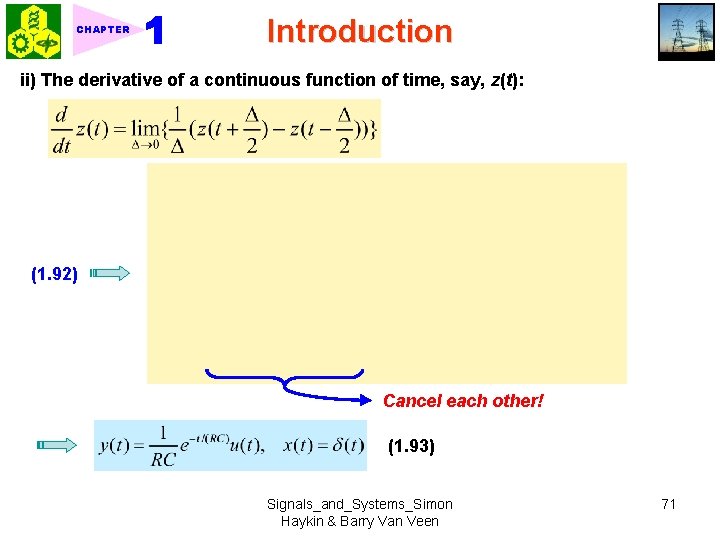
CHAPTER Introduction ii) The derivative of a continuous function of time, say, z(t): (1. 92) Cancel each other! (1. 93) Signals_and_Systems_Simon Haykin & Barry Van Veen 71

CHAPTER Introduction 1. 9 Noise Unwanted signals 1. External sources of noise: atmospheric noise, galactic noise, and humanmade noise. 2. Internal sources of noise: spontaneous fluctuations of the current or voltage signal in electrical circuit. (electrical noise) Fig. 1. 60. ★ 1. 9. 1 Thermal Noise Thermal noise arises from the random motion of electrons in a conductor. Two characteristics of thermal noise: 1. Time-averaged value: 2 T = total observation interval of noise (1. 94) As T , Refer to Fig. 1. 60. 2. Time-average-squared value: k = Boltzmann’s constant = 1. 38 10 23 J/K Tabs = absolute temperature (1. 95) As T , (1. 96) Signals_and_Systems_Simon Haykin & Barry Van Veen 72

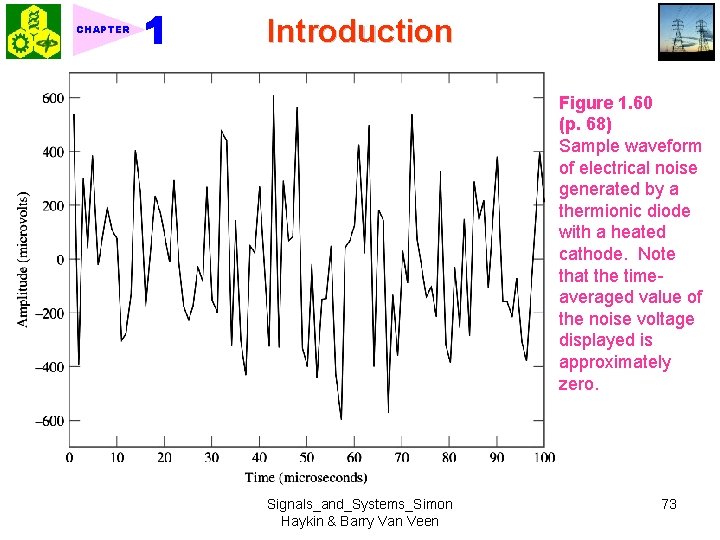
CHAPTER Introduction Figure 1. 60 (p. 68) Sample waveform of electrical noise generated by a thermionic diode with a heated cathode. Note that the timeaveraged value of the noise voltage displayed is approximately zero. Signals_and_Systems_Simon Haykin & Barry Van Veen 73

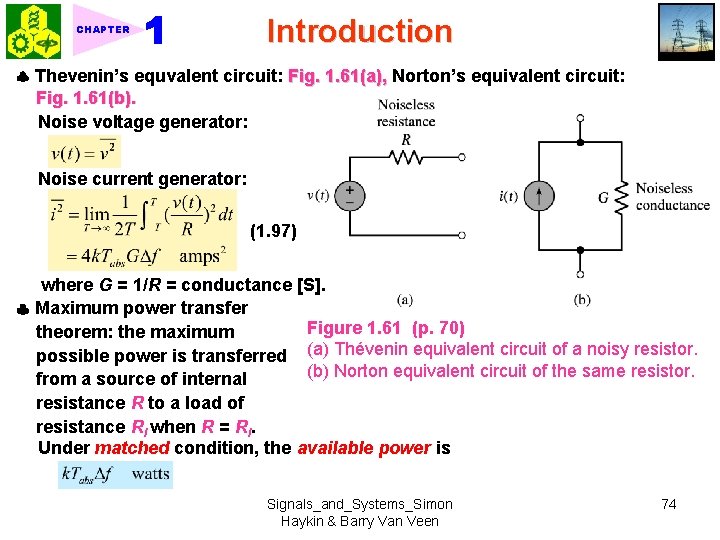
CHAPTER Introduction Thevenin’s equvalent circuit: Fig. 1. 61(a), Norton’s equivalent circuit: Fig. 1. 61(b). Noise voltage generator: Noise current generator: (1. 97) where G = 1/R = conductance [S]. Maximum power transfer Figure 1. 61 (p. 70) theorem: the maximum possible power is transferred (a) Thévenin equivalent circuit of a noisy resistor. (b) Norton equivalent circuit of the same resistor. from a source of internal resistance R to a load of resistance Rl when R = Rl. Under matched condition, the available power is Signals_and_Systems_Simon Haykin & Barry Van Veen 74

CHAPTER Introduction Two operating factor that affect available noise power: 1. The temperature at which the resistor is maintained. 2. The width of the frequency band over which the noise voltage across the resistor is measured. ★ 1. 9. 2 Other Sources of Electrical Noise 1. Shot noise: the discrete nature of current flow electronic devices 2. Ex. Photodetector: 1) Electrons are emitted at random times, k, where < k < 2) Total current flowing through photodetector: (1. 98) is the current pulse generated at time k. 3. 1/f noise: The electrical noise whose time-averaged power at a given frequency is inversely proportional to the frequency. where Signals_and_Systems_Simon Haykin & Barry Van Veen 75

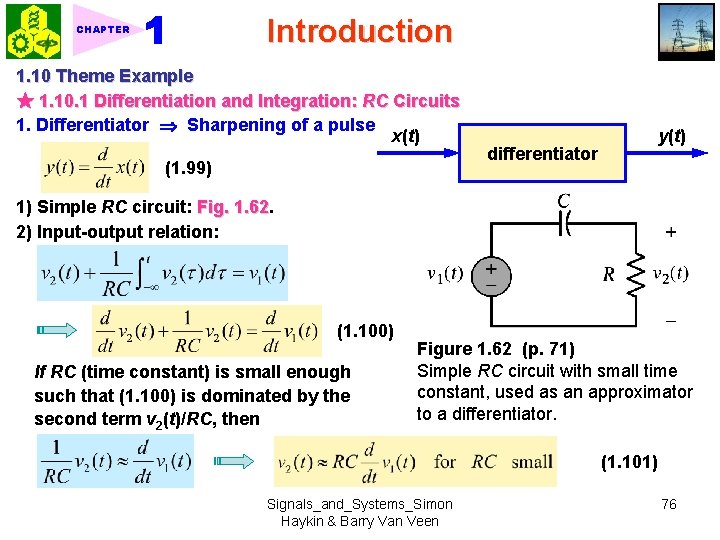
Introduction CHAPTER 1. 10 Theme Example ★ 1. 10. 1 Differentiation and Integration: RC Circuits 1. Differentiator Sharpening of a pulse x(t) (1. 99) differentiator y(t) 1) Simple RC circuit: Fig. 1. 62 2) Input-output relation: (1. 100) If RC (time constant) is small enough such that (1. 100) is dominated by the second term v 2(t)/RC, then Figure 1. 62 (p. 71) Simple RC circuit with small time constant, used as an approximator to a differentiator. (1. 101) Signals_and_Systems_Simon Haykin & Barry Van Veen 76

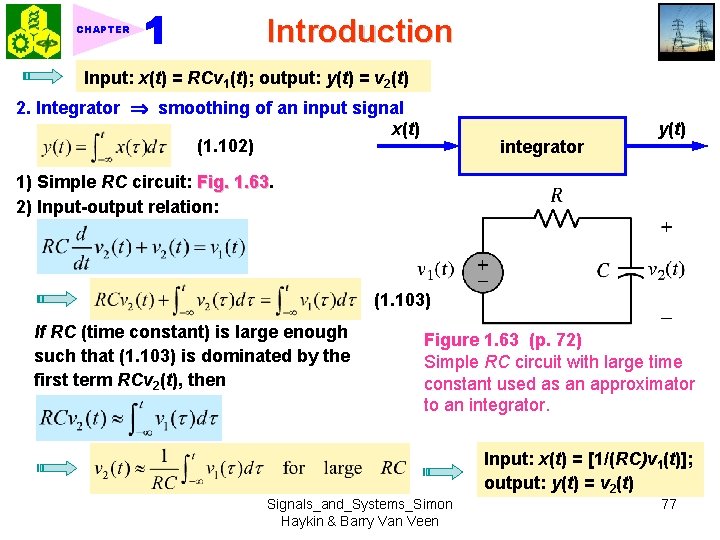
CHAPTER Introduction Input: x(t) = RCv 1(t); output: y(t) = v 2(t) 2. Integrator smoothing of an input signal x(t) (1. 102) integrator y(t) 1) Simple RC circuit: Fig. 1. 63 2) Input-output relation: (1. 103) If RC (time constant) is large enough such that (1. 103) is dominated by the first term RCv 2(t), then Figure 1. 63 (p. 72) Simple RC circuit with large time constant used as an approximator to an integrator. Input: x(t) = [1/(RC)v 1(t)]; output: y(t) = v 2(t) Signals_and_Systems_Simon Haykin & Barry Van Veen 77

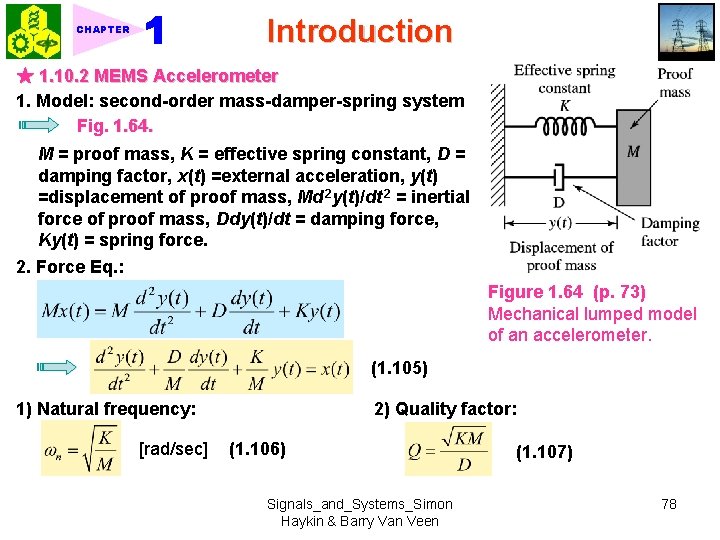
Introduction CHAPTER ★ 1. 10. 2 MEMS Accelerometer 1. Model: second-order mass-damper-spring system Fig. 1. 64. M = proof mass, K = effective spring constant, D = damping factor, x(t) =external acceleration, y(t) =displacement of proof mass, Md 2 y(t)/dt 2 = inertial force of proof mass, Ddy(t)/dt = damping force, Ky(t) = spring force. 2. Force Eq. : Figure 1. 64 (p. 73) Mechanical lumped model of an accelerometer. (1. 105) 1) Natural frequency: [rad/sec] 2) Quality factor: (1. 106) Signals_and_Systems_Simon Haykin & Barry Van Veen (1. 107) 78

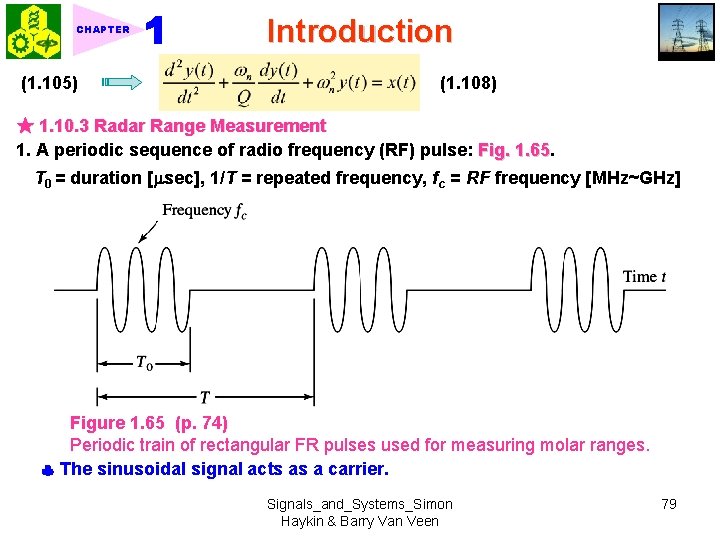
CHAPTER (1. 105) Introduction (1. 108) ★ 1. 10. 3 Radar Range Measurement 1. A periodic sequence of radio frequency (RF) pulse: Fig. 1. 65 T 0 = duration [ sec], 1/T = repeated frequency, fc = RF frequency [MHz~GHz] Figure 1. 65 (p. 74) Periodic train of rectangular FR pulses used for measuring molar ranges. The sinusoidal signal acts as a carrier. Signals_and_Systems_Simon Haykin & Barry Van Veen 79

CHAPTER Introduction 2. Round-trip time = the time taken by a radar pulse to reach the target and for the echo from the target to come back to the radar. (1. 109) d = radar target range, c = light speed. 3. Two issues of concern in range measurement: 1) Range resolution: The duration T 0 of the pulse places a lower limit on the shortest round-trip delay time that the radar can measure. Smallest target range: dmin = c. T 0/2 [m] 2) Range ambiguity: The interpulse period T places an upper limit on the largest range that the radar can measure. Largest target range: dmax = c. T/2 [m] ★ 1. 10. 4 Moving-Average Systems 1. N-point moving-average system: Fig. 1. 66. (1. 110) x(t) = input signal The value N determines the degree to which the system smooths the input data. Signals_and_Systems_Simon Haykin & Barry Van Veen 80

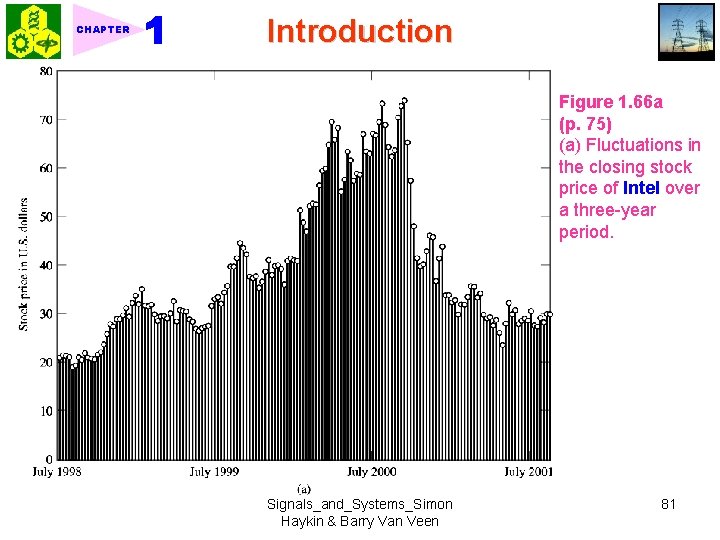
CHAPTER Introduction Figure 1. 66 a (p. 75) (a) Fluctuations in the closing stock price of Intel over a three-year period. Signals_and_Systems_Simon Haykin & Barry Van Veen 81

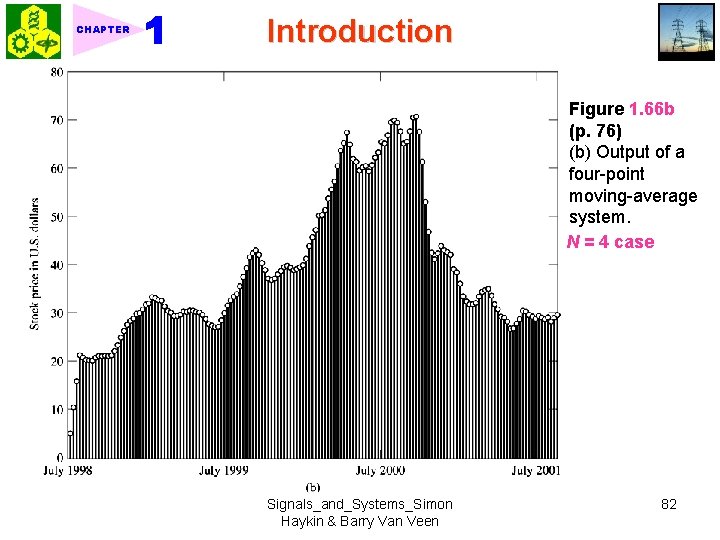
CHAPTER Introduction Figure 1. 66 b (p. 76) (b) Output of a four-point moving-average system. N = 4 case Signals_and_Systems_Simon Haykin & Barry Van Veen 82

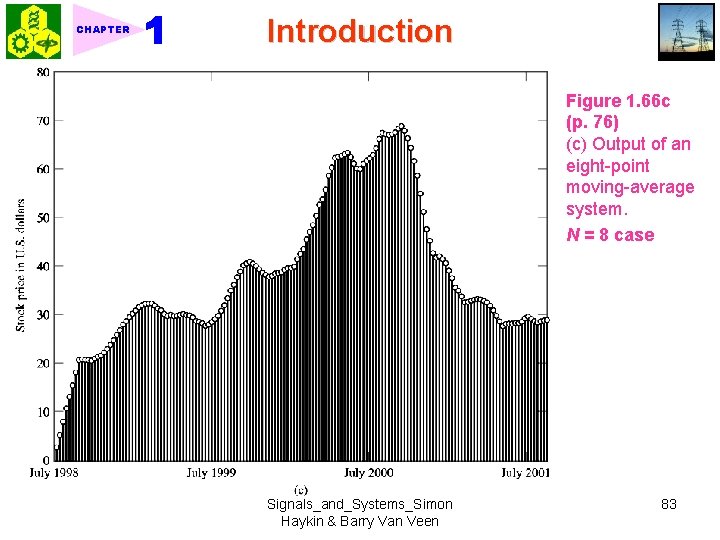
CHAPTER Introduction Figure 1. 66 c (p. 76) (c) Output of an eight-point moving-average system. N = 8 case Signals_and_Systems_Simon Haykin & Barry Van Veen 83

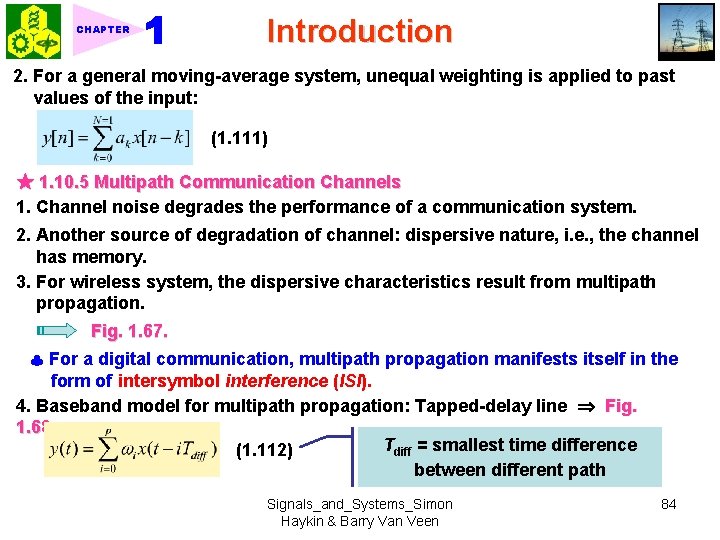
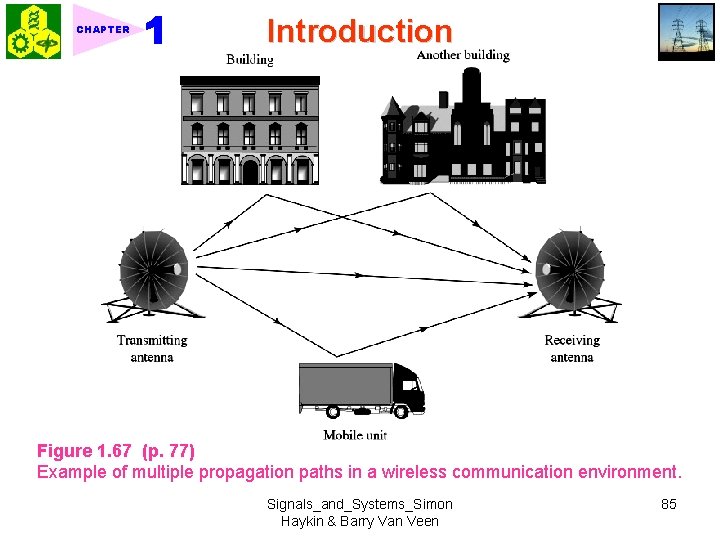
CHAPTER Introduction 2. For a general moving-average system, unequal weighting is applied to past values of the input: (1. 111) ★ 1. 10. 5 Multipath Communication Channels 1. Channel noise degrades the performance of a communication system. 2. Another source of degradation of channel: dispersive nature, i. e. , the channel has memory. 3. For wireless system, the dispersive characteristics result from multipath propagation. Fig. 1. 67. For a digital communication, multipath propagation manifests itself in the form of intersymbol interference (ISI). 4. Baseband model for multipath propagation: Tapped-delay line Fig. 1. 68 Tdiff = smallest time difference (1. 112) between different path Signals_and_Systems_Simon Haykin & Barry Van Veen 84

CHAPTER Introduction Figure 1. 67 (p. 77) Example of multiple propagation paths in a wireless communication environment. Signals_and_Systems_Simon Haykin & Barry Van Veen 85

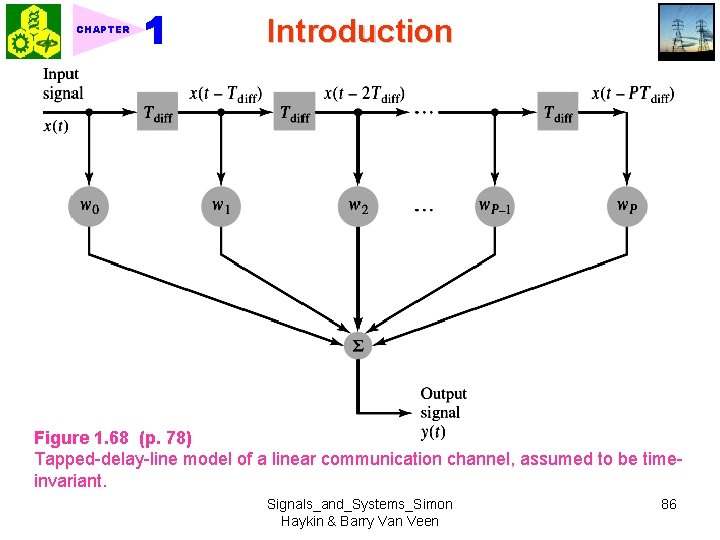
CHAPTER Introduction Figure 1. 68 (p. 78) Tapped-delay-line model of a linear communication channel, assumed to be timeinvariant. Signals_and_Systems_Simon Haykin & Barry Van Veen 86

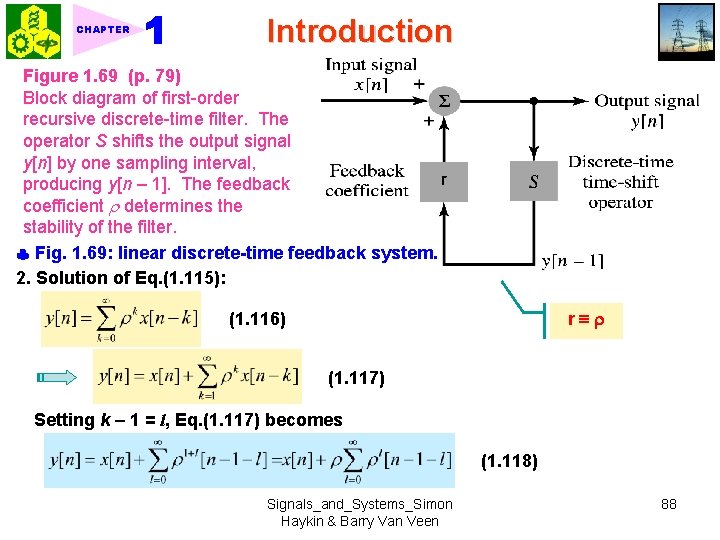
CHAPTER Introduction 5. PTdiff = the longest time delay of any significant path relative to the arrival of the signal. The coefficients wi are used to approximate the gain of each path. For P =1, then 0 x(t) = direct path, 1 x(t Tdiff) = single reflected path 6. Discrete-time case: Linearly weighted moving-average system (1. 113) For P =1, then (1. 114) ★ 1. 10. 6 Recursive Discrete-Time Computations The term recursive signifies the dependence of the output signal on its own past values. 1. First-order recursive discrete-time filter: Fig. 1. 69 (1. 115) x[n] = input, y[n] = output where is a constant. Signals_and_Systems_Simon Haykin & Barry Van Veen 87

CHAPTER Introduction Figure 1. 69 (p. 79) Block diagram of first-order recursive discrete-time filter. The operator S shifts the output signal y[n] by one sampling interval, producing y[n – 1]. The feedback coefficient determines the stability of the filter. Fig. 1. 69: linear discrete-time feedback system. 2. Solution of Eq. (1. 115): r (1. 116) (1. 117) Setting k 1 = l, Eq. (1. 117) becomes (1. 118) Signals_and_Systems_Simon Haykin & Barry Van Veen 88

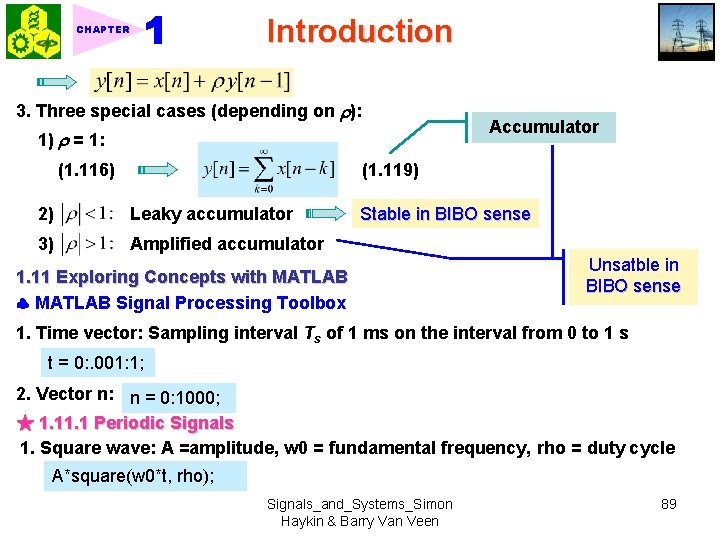
Introduction CHAPTER 3. Three special cases (depending on ): 1) = 1: (1. 116) Accumulator (1. 119) 2) Leaky accumulator 3) Amplified accumulator Stable in BIBO sense 1. 11 Exploring Concepts with MATLAB Signal Processing Toolbox Unsatble in BIBO sense 1. Time vector: Sampling interval Ts of 1 ms on the interval from 0 to 1 s t = 0: . 001: 1; 2. Vector n: n = 0: 1000; ★ 1. 1 Periodic Signals 1. Square wave: A =amplitude, w 0 = fundamental frequency, rho = duty cycle A*square(w 0*t, rho); Signals_and_Systems_Simon Haykin & Barry Van Veen 89

CHAPTER Introduction Ex. Obtain the square wave shown in Fig. 1. 14 (a) by using MATLAB. <Sol. > >> A = 1; >> w 0 =10*pi; >> rho = 0. 5; >> t = 0: . 001: 1; >> sq = A*square(w 0*t, rho); >> plot (t, sq) >> axis([0 1 -1. 1]) 2. Triangular wave: A =amplitude, w 0 = fundamental frequency, w = width A*sawtooth(w 0*t, w); Ex. Obtain the triangular wave shown in Fig. 1. 15 by using MATLAB. <Sol. > >> A = 1; >> w 0 =10*pi; >> w = 0. 5; >> t = 0: 0. 001: 1; >> tri = A*sawtooth(w 0*t, w); >> plot (t, tri) Signals_and_Systems_Simon Haykin & Barry Van Veen 90

CHAPTER Introduction 3. Discrete-time signal: stem(n, x); x = vector, n = discrete time vector Ex. Obtain the discrete-time square wave shown in Fig. 1. 16 by using MATLAB. <Sol. > >> A = 1; >> omega =pi/4; >> n = -10: 10; >> x = A*square(omega*n); >> stem(n, x) 4. Decaying exponential: B*exp(-a*t); Growing exponential: B*exp(a*t); Ex. Obtain the decaying exponential signal shown in Fig. 1. 28 (a) by using MATLAB. <Sol. > >> B = 5; >> a = 6; >> t = 0: . 001: 1; >> x = B*exp(-a*t); % decaying exponential >> plot (t, x) Signals_and_Systems_Simon Haykin & Barry Van Veen 91

CHAPTER Introduction Ex. Obtain the growing exponential signal shown in Fig. 1. 28 (b) by using MATLAB. <Sol. > >> B = 1; >> a = 5; >> t = 0: 0. 001: 1; >> x = B*exp(a*t); % growing exponential >> plot (t, x) Ex. Obtain the decaying exponential sequence shown in Fig. 1. 30 (a) by using MATLAB. <Sol. > >> B = 1; >> r = 0. 85; >> n = -10: 10; >> x = B*r. ^n; % decaying exponential sequence >> stem (n, x) ★ 1. 11. 3 Sinusoidal Signals 1. Cosine signal: A*cos(w 0*t + phi); 2. Sine signal: A*sin(w 0*t + phi); Signals_and_Systems_Simon Haykin & Barry Van Veen A = amplitude, w 0 = frequency, phi = phase angle 92

CHAPTER Introduction Ex. Obtain the sinusoidal signal shown in Fig. 1. 31 (a) by using MATLAB. <Sol. > >> A = 4; >> w 0 =20*pi; >> phi = pi/6; >> t = 0: . 001: 1; >> cosine = A*cos(w 0*t + phi); >> plot (t, cosine) Ex. Obtain the discrete-time sinusoidal signal shown in Fig. 1. 33 by using MATLAB. <Sol. > >> A = 1; >> omega =2*pi/12; % angular frequency. * element-by-element >> n = -10: 10; multiplication >> y = A*cos(omega*n); >> stem (n, y) ★ 1. 11. 4 Exponential Damped Sinusoidal Signals 1. Exponentially damped sinusoidal signal: MATLAB Format: A*sin(w 0*t + phi). *exp(-a*t); Signals_and_Systems_Simon Haykin & Barry Van Veen 93

CHAPTER Introduction Ex. Obtain the waveform shown in Fig. 1. 35 by using MATLAB. <Sol. > >> A = 60; >> w 0 =20*pi; >> phi = 0; >> a = 6; >> t = 0: . 001: 1; >> expsin = A*sin(w 0*t + phi). *exp(-a*t); >> plot (t, expsin) Ex. Obtain the exponentially damped sinusoidal sequence shown in Fig. 1. 70 by using MATLAB. <Sol. > >> A = 1; >> omega =2*pi/12; % angular frequency >> n = -10: 10; >> y = A*cos(omega*n); >> r = 0. 85; >> x = A*r. ^n; % decaying exponential sequence >> z = x. *y; % elementwise multiplication >> stem (n, z) Signals_and_Systems_Simon Haykin & Barry Van Veen 94

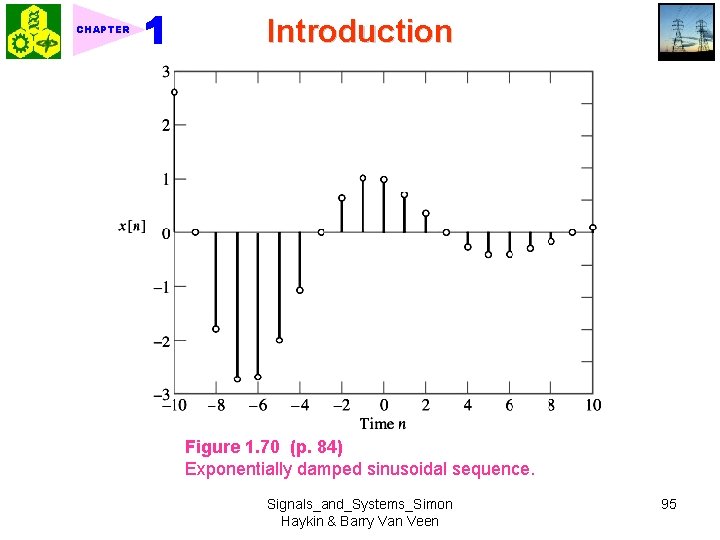
CHAPTER Introduction Figure 1. 70 (p. 84) Exponentially damped sinusoidal sequence. Signals_and_Systems_Simon Haykin & Barry Van Veen 95

CHAPTER Introduction ★ 1. 11. 5 Step, Impulse, and Ramp Functions ◆ MATLAB command: 1. M-by-N matrix of ones: ones (M, N) 2. M-by-N matrix of zeros: zeros (M, N) Ex. Generate a rectangular pulse centered at origin on the interval [-1, 1]. <Sol. > Unit amplitude step function: u = [zeros(1, 50), ones(1, 50)]; Discrete-time impulse: delta = [zeros(1, 49), 1, zeros(1, 49)]; >> t = -1: 1/500: 1; >> u 1 = [zeros(1, 250), ones(1, 751)]; >> u 2 = [zeros(1, 751), ones(1, 250)]; >> u = u 1 – u 2; Ramp sequence: ramp = 0: . 1: 10 ★ 1. 11. 6 User-Defined Functions 1. Two types M-files exist: scripts and functions. Scripts, or script files automate long sequences of commands; functions, or function files, provide extensibility to MATLAB by allowing us to add new functions. 2. Procedure for establishing a function M-file: Signals_and_Systems_Simon Haykin & Barry Van Veen 96

CHAPTER Introduction 1) It begins with a statement defining the function name, its input arguments, and its output arguments. 2) It also includes additional statements that compute the values to be returned. 3) The inputs may be scalars, vectors, or matrices. Ex. Obtain the rectangular pulse depicted in Fig. 1. 39 (a) with the use of an M-file. 1. The function size returns a two<Sol. > element vector containing the row >> function g = rect(x) and column dimensions of a matrix. >> g = zeros(size(x)); 2. The function find returns the >> set 1 = find(abs(x)<= 0. 5); indices of a vector or matrix that >> g(set 1) = ones(size(set 1)); satisfy a prescribed relation 3. The new function rect. m can be used liked any other MATLAB function. Ex. find(abs(x)<= T) returns the indices Ex. To generate a rectangular pulse: of the vector x, where the absolute >> t = -1: 1/500: 1; value of x is less than or equal to T. >> plot(t, rect(t)); Signals_and_Systems_Simon Haykin & Barry Van Veen 97

CHAPTER Introduction Signals_and_Systems_Simon Haykin & Barry Van Veen 98