INTRODUCERE Transformrile grafice sunt operaii geometrice liniare sau

INTRODUCERE Transformările grafice sunt operaţii geometrice liniare sau neliniare, având ca operanzi formele grafice. Cele mai uzitate tipuri de transformări grafice sunt: - transformări bidimensionale - transformări tridimensionale

TRANSFORMĂRI BIDIMENSIONALE Transformările bidimensionale sunt operaţii de trecere între spaţii de dimensiune 2. Cele mai cunoscute tipuri de transformări grafice bidimensionale sunt: - translarea - rotaţia - scalarea - oglindirea - forfecarea

TRANSLAREA 2 D Translarea se definește ca fiind transformarea grafică pentru care orice punct al formei suferă o deplasare liniară global definită. Translarea este o transformare grafică ce lasă nemodificate distanțele între punctele unei forme grafice. Acestă caracteristică este specifică corpurilor fizice solide (nedeformabile) și de aceea o vom numi caracteristică de corp solid. Reformulând, putem spune că transformarea grafică numită translare prezintă caracteristica de corp solid. Operația de translare poate fi definită cel puțin două puncte de vedere: ALFA şi BETA.

(ALFA)TRANSLAREA 2 D Fie punctul P de coordonate (xp, yp) și punctul Q de coordonate (xq, yq). Distanța între aceste două puncte este definită ca fiind: Y P(xp, yp) yp D Dy Q(xq, yq) yq O xp Dx xq Fig. 1. Translarea ca deplasare între puncte X

(ALFA) TRANSLAREA 2 D •

(ALFA) TRANSLAREA 2 D Observație: Expresia matriceală normală ar trebui să fie de forma: unde matricea este operatorul transformării. În condițiile date, însă, o astfel de scriere, în care componentele operatorului să fie constante reale, nu este posibilă. Din acest motiv vor fi introduse mai târziu coordonatele omogene. În cazul dat, coeficienții matricei operatorului transformării ar trebui să fie conformi cu: Se observă că și nu sunt constante independente de punctele extreme ale deplasării.

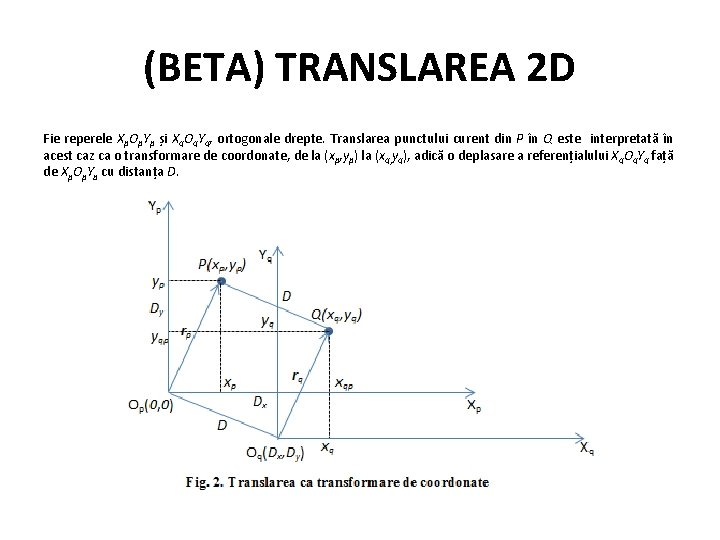
(BETA) TRANSLAREA 2 D Fie reperele Xp. Op. Yp și Xq. Oq. Yq, ortogonale drepte. Translarea punctului curent din P în Q este interpretată în acest caz ca o transformare de coordonate, de la (xp, yp) la (xq, yq), adică o deplasare a referențialului Xq. Oq. Yq față de Xp. Op. Yp cu distanța D.

(BETA) TRANSLAREA 2 D

SCALAREA 2 D • Transformarea grafică de scalare se definește ca fiind operația prin care forma grafică suferă o modificare de reprezentare în urma căreia distanțele dintre puncte sunt afectate. • Fiecărei axe de coordonate i se atașează un scalar numit factor de scară. Atunci când factorii de scară au aceeași valoare, operația de scalare se transformă în operație de asemănare iar factorul de scalare unic definit poartă numele de factor de asemănare. Factorul de asemănare unitate conduce la operația de identitate. • Un factor de scalare supraunitar specifică o mărire de dimensiune în timp ce un factor de scalare subunitar conduce la o micșorare de dimensiune.

SCALAREA 2 D •

SCALAREA 2 D Asemănarea se va exprima astfel: cu: sx=sy=s Observaţie: Se poate observa că în analiza făcută, originea (ca punct) prezintă un rol special, constituind punctul fix al transformării. În cazul general, punctul fix al transformării poate fi oricare punct din spațiul transformării.

SCALAREA 2 D •

ROTAŢIA 2 D

ROTAŢIA 2 D După transformările trigonometrice specifice sumei de argument, obţinem: Expresia matriceal-vectorială corespondentă este:

ROTAŢIA 2 D Rezultă că matricea transformării este: Transformarea de rotaţie se rescrie astfel:

ROTAŢIA 2 D Dacă matricea transformării este nesingulară: există transformarea inversă:

COMPUNEREA TRANSFORMĂRILOR 2 D De cele mai multe ori o transformare grafică este compusă din mai multe transformări elementare. Pentru simplificarea reprezentărilor matematice, se preferă utilizarea notației matriceale în descrierea operațiilor de transformare. Astfel, rotația punctului P(x, y) față de origine, se exprimă astfel: sau: Sintetic se poate scrie:

COMPUNEREA TRANSFORMĂRILOR 2 D Considerăm în continuare o scalare față de origine urmată de o rotație față de origine. Avem: cu: Observație: Deoarece produsul matriceal nu este comutativ, va trebui acordată atenție succesiunii matricelor ce semnifică operatorii transformărilor. Regula este ca matricea să se succeadă în ordinea în care acestea operează, de la dreapta la stânga. Astfel, o transformare compusă dintr-o rotație urmată de o scalare se scrie: În timp ce o transformare compusă dintr-o scalare urmată de o rotație se scrie: Exercițiu: Să se demonstreze că cele două transformări sunt distincte.

COORDONATE OMOGENE Coordonatele omogene au fost introduse de Möbius. August Ferdinand Möbius (n. 17 noiembrie 1790 - d. 26 septembrie 1868) a fost un matematician și un astronom german. Este cunoscut mai ales pentru descoperirea unei suprafețe speciale, denumite ulterior bandă Möbius este primul care a introdus coordonatele omogene în geometria proiectivă. Alte concepte matematice care i se atribuie sunt: transformările lui Möbius din geometria proiectivă, funcția lui Möbius din teoria numerelor și formula de inversiune a lui Möbius. Coordonatele omogene permit transformări afine prin reprezentarea lor sub forma unei matrice. Ele permit, de asemenea, efectuarea calculelor în spații proiective într-un mod similar cu cel în care coordonatele carteziene o fac în spaţiul euclidian. Din punct de vedere intuitiv, coordonatele omogene reprezintă componentele vectoriale ce construiesc vectorii de poziţie ai mulţimii punctelor (x, y, w) de pe planul (w=const) ce constituie proiecţia universului înconjurător. Punctele din planul constituie intersecţia dreptelor de proiecţie a punctelor din univers cu planul , atunci când razele de proiecţie trec prin originea sistemului de coordonate (punctul fix proiectiv este originea).

COORDONATE OMOGENE Dacă se va încerca exprimarea unor transformări compuse ce cuprind în secvență cel puțin o translare, reprezentările matriceale acestora (după modelul prezentat) nu vor mai fi posibile fără a apela la coordonatele omogene. Un punct din plan, notat (x, y), se reprezintă în coordonate omogene prin vectorul: unde: și . Observație 1: Reprezentarea unui punct în coordonate omogene nu este unică. Astfel, vectorii: , și sunt reprezentări posibile ale punctului (3, 2) în coordonate omogene. Observație 2: Un vector în coordonate omogene , , reprezintă punctul din plan notat .

COORDONATE OMOGENE Observaţie: Punctul este punctul de la infinit situat pe dreapta ay-bx=0 (această ecuaţie rezultă din ). Rezultă: este punctul de la infinit de pe semiaxa pozitivă Ox este punctul de la infinit de pe semiaxa negativă Oy este punctul de la infinit de pe dreapta y=x în direcţia

COORDONATE OMOGENE Cele trei transformări discutate (translarea, scalarea şi rotaţia) în coordonate omogene, capătă următoarele exprimări: - translarea: - scalarea faţă de origine: - rotaţia faţă de origine:

COORDONATE OMOGENE Expresiile matematice ale scalării şi rotaţiei faţă de un punct oarecare din plan, se pot obţine prin compunerea următoarelor transformări: 1. translarea în urma căreia punctul fix al transformării ajunge în origine; 2. scalarea/rotaţia faţă de origine; 3. translarea inversă celei de la punctul 1. Ecuaţiile matriceale sunt: unde: respectiv şi .

COORDONATE OMOGENE Transformări inverse Fiecare dintre transformările elementare deţine o operaţie inversă (o transformare opusă). Se pot verifica proprietăţile: 1. 2. 3.

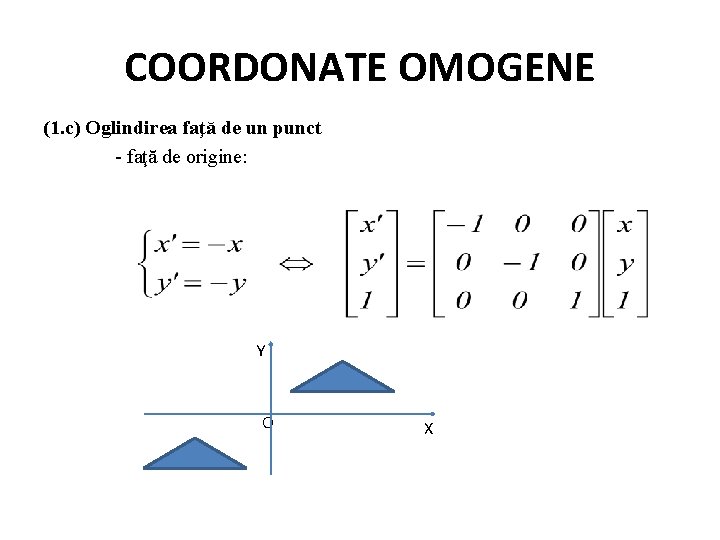
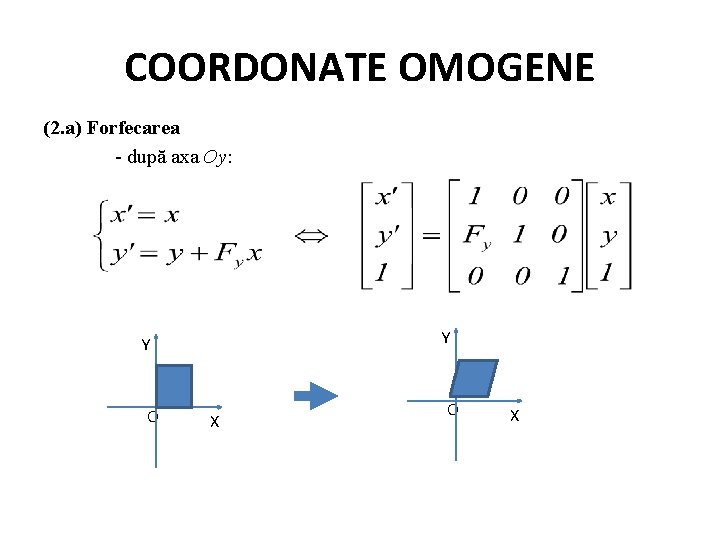
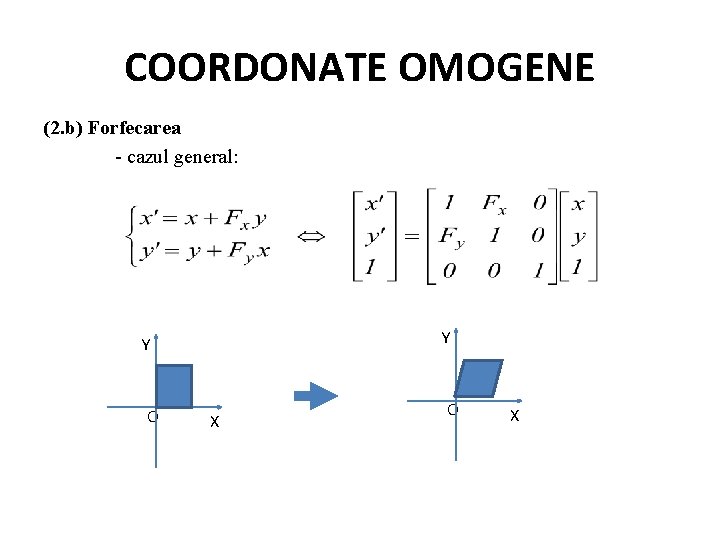
COORDONATE OMOGENE Alte transformări 1. Oglindirea (Reflexia) 2. Forfecarea 1. Oglindirea (a) – faţă de o axă (b) – faţă de o dreaptă oarecare (c) – faţă de un punct 2. Forfecarea (a) – după o axă (b) – după o dreaptă oarecare

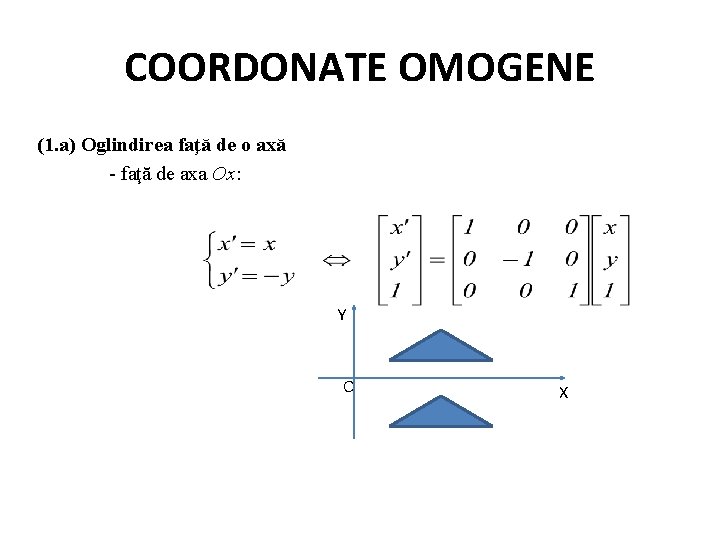
COORDONATE OMOGENE (1. a) Oglindirea faţă de o axă - faţă de axa Ox: Y O X

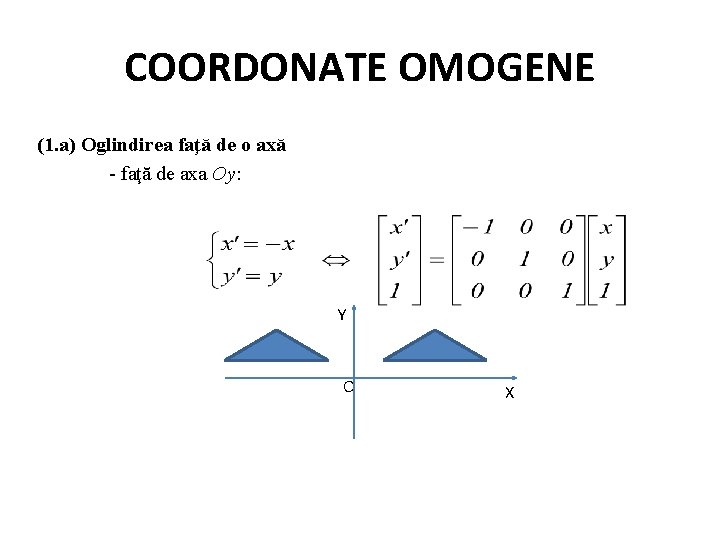
COORDONATE OMOGENE (1. a) Oglindirea faţă de o axă - faţă de axa Oy: Y O X

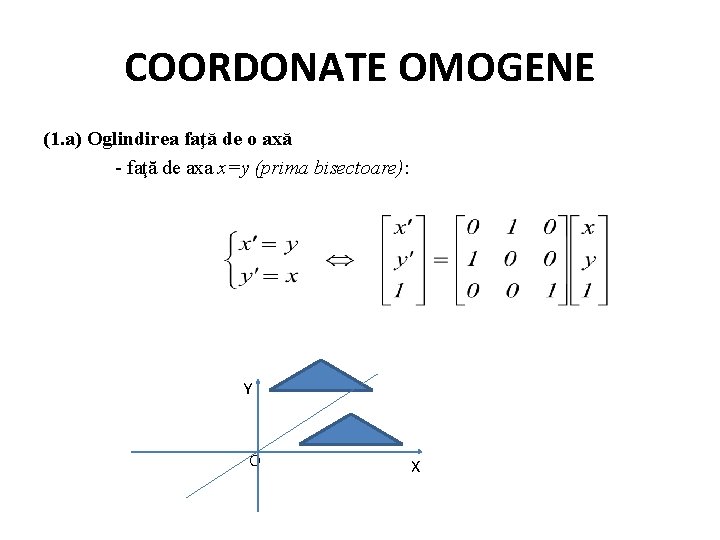
COORDONATE OMOGENE (1. a) Oglindirea faţă de o axă - faţă de axa x=y (prima bisectoare): Y O X

COORDONATE OMOGENE (1. b) Oglindirea faţă de o dreaptă oarecare Această transformare se poate defini ca fiind transformarea compusă din următoarea secvenţă: 1. 2. 3. 4. 5. translare astfel încât dreapta să treacă prin origine; rotaţie faţă de origine astfel încât dreapta să se suprapună peste una dintre axele principale; oglindire faţă de axa principală respectivă; rotaţie inversă celei de la punctul 2; translare inversă celei de la punctul 1. În notaţie matriceală transformarea se exprimă astfel: Observaţie: Exerciţiu: Să se demonstreze afirmaţia de mai sus pentru cazul oglindirii faţă de prima bisectoare.

COORDONATE OMOGENE (1. c) Oglindirea faţă de un punct - faţă de origine: Y O X

COORDONATE OMOGENE (2. a) Forfecarea - după axa Ox: Y Y O X

COORDONATE OMOGENE (2. a) Forfecarea - după axa Oy: Y Y O X

COORDONATE OMOGENE (2. b) Forfecarea - cazul general: Y Y O X