Introduccin a Wavelets Onditas Jaime Gaviria Introduccin Esta

Introducción a Wavelets (Onditas) Jaime Gaviria

Introducción Esta presentación busca realizar una introducción de una forma sencilla al concepto de wavelet y básicamente es una recopilación de artículos y tesis que hablan del tema. Las Fuentes son citadas al final de la presentación.

Introducción l l Las necesidades actuales en procesamiento de señales requieren “nuevos” mecanismos y tecnicas de análisis El manejo de señales con discontinuidades y cambios abruptos no pueden ser manejadas adecuadamente con tecnicas de Fourier

Introducción l Buscar una forma más “humana” de análisis, los wavelets sintetizan información de la forma en que lo haría el cerebro

Introducción l En la actualidad el mundo esta invadido de “wavelets” se usan multiples aplicaciones, como animación, procesamiento de imágenes, análisis y síntesis de audio, ingeniería minera, predicciones meteorológicas, estudios de astronomía, diagnóstico de enfermedades, etc

Una Explicación Sencilla l l l Como hace el cerebro para identificar entre un instrumento y otro en una banda Como hace el cerebro para identificar entre un árbol y otro en un bosque? Como lo hacen los wavelets?

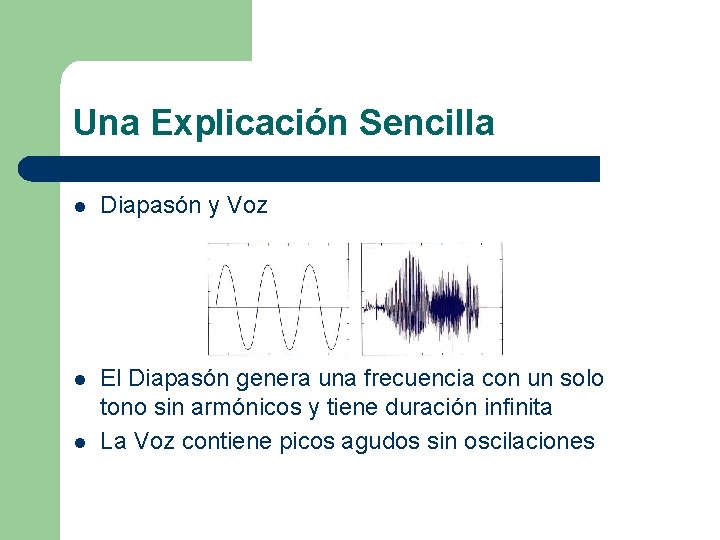
Una Explicación Sencilla l Diapasón y Voz l El Diapasón genera una frecuencia con un solo tono sin armónicos y tiene duración infinita La Voz contiene picos agudos sin oscilaciones l

Una Explicación Sencilla l l Para el caso del diapasón, que genera una señal periódica, se puede realizar el análisis de la señal usando fourier de modo que se descompone la señal en componentes sinusoidales de diversas frecuencias y una frecuencia fundamental Si tenemos dos instrumentos, como una flauta y un violín, aunque la nota de la frecuencia fundamental sea la misma, su sonido es distinto, esto se debe a los pesos de sus armónicos

Una Explicación Sencilla l l Para las señales no periódicas, tambien existe análisis de Fourier, en el cual se pueden clasificar la mayoría de señales existentes en el mundo real, como el ruido de un carro. Las características no repetitivas, pueden analizarse mediante la transformada de fourier, como ejemplo, un ruido del motor del carro.

Algo de Historia l l El análisis de Fourier se venía usando practicamente para el manejo de cualquier tipo de señales, sin embargo, produce dificultades a la hora de analizar señales fugaces o cambios abruptos como la palabra hablada Como ejemplo, los sintetizadores de música, se basan en Fourier, pero por bien diseñados que esten, no logran reproducir un instrumento real, pues la interpretación de un instrumento esta llena de cambios y picos abruptos

Algo de Historia l El principio de éste problema se puede resumir en la “indeterminación de Heisenberg” “La posición y la velocidad de un objeto no se pueden medir exactamente al mismo tiempo, ni siquiera en teoría”

Algo de Historia l l Es imposible conocer de forma simultánea la frecuencia exacta y el momento exacto en que ocurre esta frecuencia en una señal. Para poder conocer la frecuencia, la señal se debe dilatar en el tiempo, o viceversa. Cualquier señal de duración corta debe tener un complejo espectro de frecuencias formado por una gran variedad de ondas sinusoidales, Cualquier señal formada por una combinación simple de unas pocas ondas sinusoidales debe tener una apariencia compleja en el dominio del tiempo En otras palabras, no podemos esperar reproducir el sonido de un tambor, con una orquesta de diapasones.

Algo de Historia l l Ante este problema, se buscó una solución que permitiera trabajar con una señal tanto a baja como a alta resolución, en diferentes ámbitos, llegando a la conclusión, de que era algo que no se iba a lograr con fourier Quizás al dividir una señal en componentes que no fueran ondas sinusoidales puras sería posible condensar la información tanto en el dominio del tiempo como en el de la frecuencia?

La Carrera de las Wavelets l Alfred Haar, introdujo en 1909 las funciones que actualmente se denominan "wavelets de Haar" que consisten en un breve impulso positivo seguido de uno negativo, producen picos y no suavidad

La Carrera de las Wavelets l En la década de 1930, John Littlewood y R. E. A. C. Paley desarrollaron un método de agrupación de frecuencias por octavas, creando de esta forma una señal con una frecuencia bien localizada (su espectro se encuentra dentro de una octava) y también relativamente bien localizada en el tiempo

La Carrera de las Wavelets l 1946, Dennis Gabor, presentó la transformación de Gabor, análoga a la transformación de Fourier, que separa una onda en "paquetes de tiempo-frecuencia" o "estados coherentes" que tienen la mayor localización simultánea posible tanto en tiempo como en frecuencia.

La Carrera de las Wavelets l En las décadas de 1970 y 1980, las comunidades de procesamiento de señales y procesamiento de imágenes presentaron sus propias versiones del análisis de wavelets con nombres tales como "codificación de subbandas", "filtros de duplicación de cuadratura" y "algoritmo piramidal".

La Carrera de las Wavelets l l Todas estas técnicas tenían características similares. Descomponían o transformaban señales en partes que se podían localizar en cualquier intervalo de tiempo y que también se podían dilatar o contraer para analizar la señal a distintas escalas de resolución. En 1984, la teoría de las wavelets adoptó finalmente su carácter propio

La Carrera de las Wavelets l Morlet buscaba una mejor forma de buscar petroleo desarrolló su propia forma de analizar las señales sísmicas para crear componentes que estuvieran localizados en el espacio, a los que denominó "wavelets de forma constante"

La Carrera de las Wavelets l l Se pueden construir familias de wavelets adoptando una forma diferente, denominada wavelet madre, y dilatándola, comprimiéndola o desplazándola en el tiempo. La wavelet madre afecta enormemente a las propiedades de compresión y precisión de la aproximación

La Carrera de las Wavelets l l Meyer, despues de descubrir diversas formas de wavelets , descubrió una con la propiedad de ortogonalidad que hacía que manipular y trabajar con la transformación de wavelets resultara tan fácil como con una transformación de Fourier. Mallat, en colaboración con Meyer, demostró que las wavelets están implícitas en el procesos del análisis multiresolución.

La Carrera de las Wavelets l Gracias al trabajo de Mallat, en el campo del procesamiento de imágenes, las wavelets se convirtieron en algo mucho más sencillo. Ya se podía hacer un análisis de wavelets sin necesidad de conocer la fórmula de una wavelet madre

La Carrera de las Wavelets l l Ingrid Daubechies, descubrió una clase completamente nueva de wavelets, que no sólo eran ortogonales (como las de Meyer) sino que también se podían implementar mediante sencillas ideas de filtrado digital, de hecho, mediante cortos filtros digitales. Los procesadores de señales disponían ahora de una herramienta de ensueño: una manera de descomponer datos digitales en contribuciones de diversas escalas.

Ahora si, Wavelets! l Gráficos de varios tipos distintos de wavelets. (a) Wavelet de Haar, (b) Wavelet de Daubechies, (c) Wavelet de Morlet.

Ahora si, Wavelets! l l (a) Las imágenes superiores muestran la señal original, que presenta saltos y tramos suaves (b) una versión con ruido de la señal, de la que se desearía "eliminar el ruido" (c) En la parte inferior, el resultado de la eliminación de ruido mediante las wavelets de Haar produce una línea irregular (d) en contraste, si se utilizan las wavelets de Daubechies producen una curva más suave

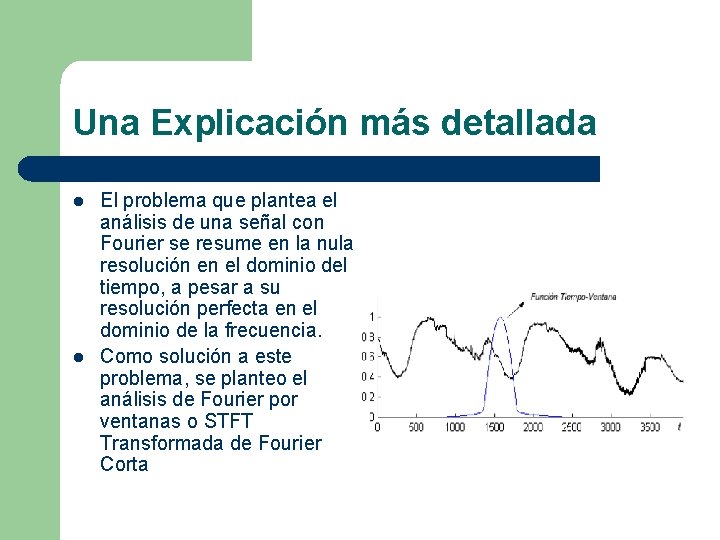
Una Explicación más detallada l l El problema que plantea el análisis de una señal con Fourier se resume en la nula resolución en el dominio del tiempo, a pesar a su resolución perfecta en el dominio de la frecuencia. Como solución a este problema, se planteo el análisis de Fourier por ventanas o STFT Transformada de Fourier Corta

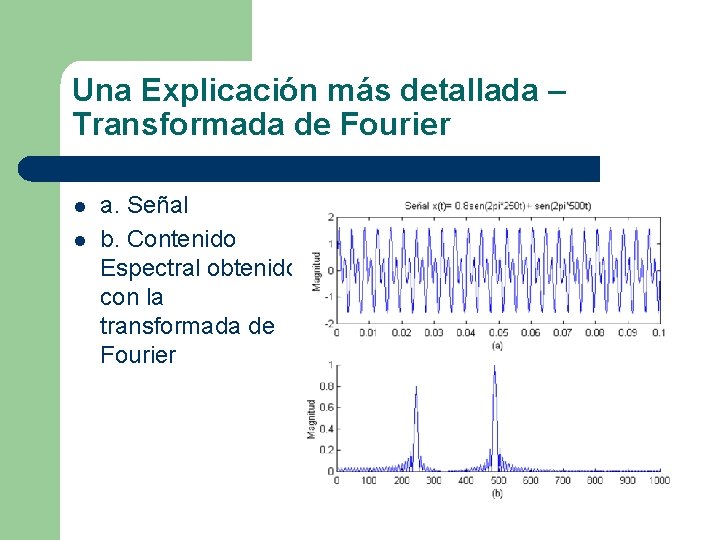
Una Explicación más detallada – Transformada de Fourier l l a. Señal b. Contenido Espectral obtenido con la transformada de Fourier

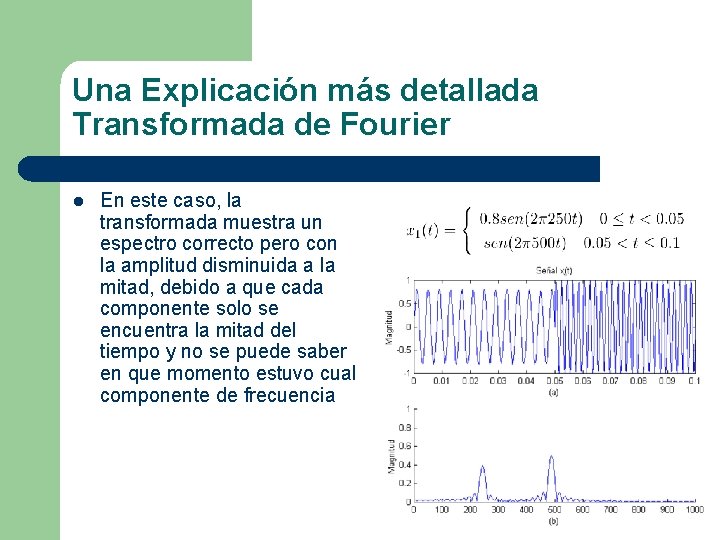
Una Explicación más detallada Transformada de Fourier l En este caso, la transformada muestra un espectro correcto pero con la amplitud disminuida a la mitad, debido a que cada componente solo se encuentra la mitad del tiempo y no se puede saber en que momento estuvo cual componente de frecuencia

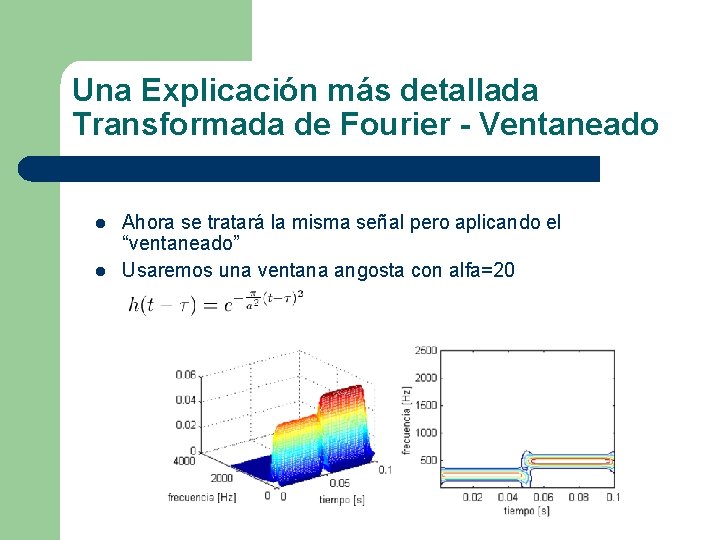
Una Explicación más detallada Transformada de Fourier - Ventaneado l l Ahora se tratará la misma señal pero aplicando el “ventaneado” Usaremos una ventana angosta con alfa=20

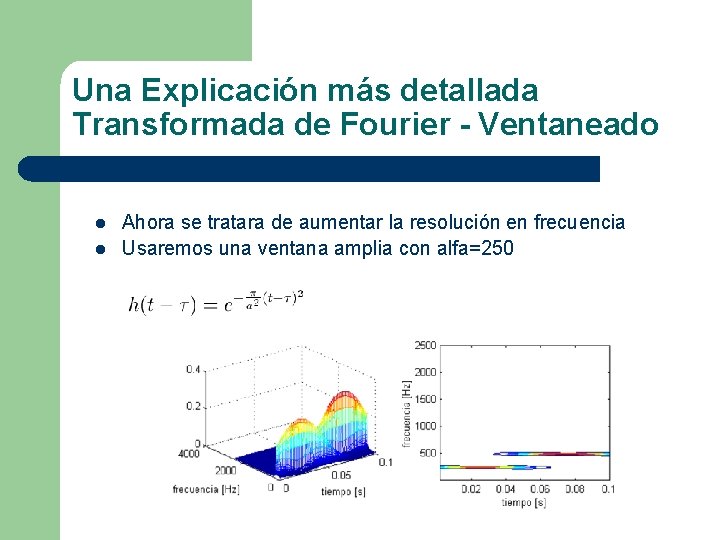
Una Explicación más detallada Transformada de Fourier - Ventaneado l l Ahora se tratara de aumentar la resolución en frecuencia Usaremos una ventana amplia con alfa=250

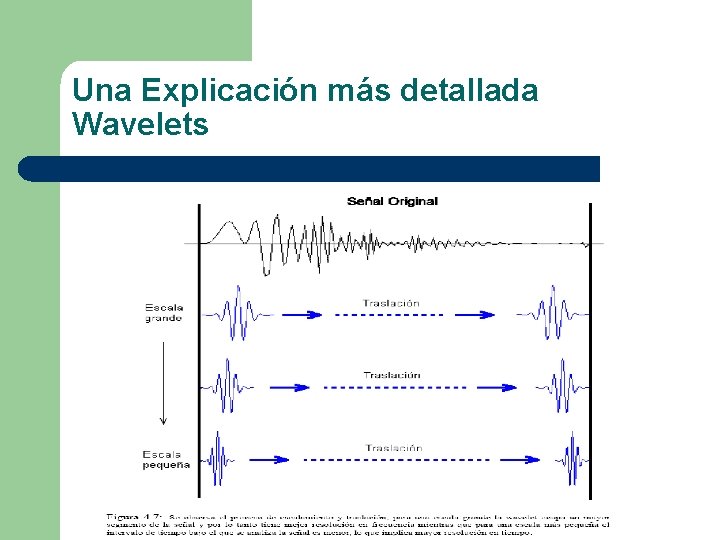
Una Explicación más detallada Wavelets l l La transformada wavelet constituye una técnica para el análisis del comportamiento local de una señal. Al igual que la STFT, esta transformada utiliza una función ventana que encuadra una señal dentro de un intervalo y focaliza el análisis sólo en ese segmento de la señal. La transformada continua wavelet intenta expresar una señal x(t)continua en el tiempo, mediante una expansión de términos o coeficientes proporcionales al producto interno entre la señal y diferentes versiones escaladas y trasladadas de una función prototipo Y(t) más conocida como wavelet madre

Una Explicación más detallada Wavelets l l Transformada continua wavelet a controla el ancho o soporte efectivo de la función , y la variable b da la ubicación en el dominio del tiempo de Y

Una Explicación más detallada Wavelets l ψ(0)=0, significa que el valor medio de φ=0 por lo que φ debe tener valores positivos y negativos, de modo que φ debe ser una onda, además como esta definida por a y b en un intervalo de tiempo, la onda es compacta. φ decae cuando w=0, y puede ser considerada como un filtro pasabanda

Una Explicación más detallada Wavelets – Variables de escala a y traslación b l l l Mediante la variable de escala nosotros podemos comprimir (!a! < 1) o dilatar (!a! > 1) la función (t), lo que dará el grado de resolución con el cual se está analizando la señal. Por definición la Transformada Continua Wavelet es mas una representación tiempo - escala que una representación tiempo - frecuencia. para escalas pequeñas la CWT nos entrega una buena resolución en el dominio del tiempo mientras que para escalas grandes la CWT nos entrega una buena resolución en el dominio de la frecuencia.

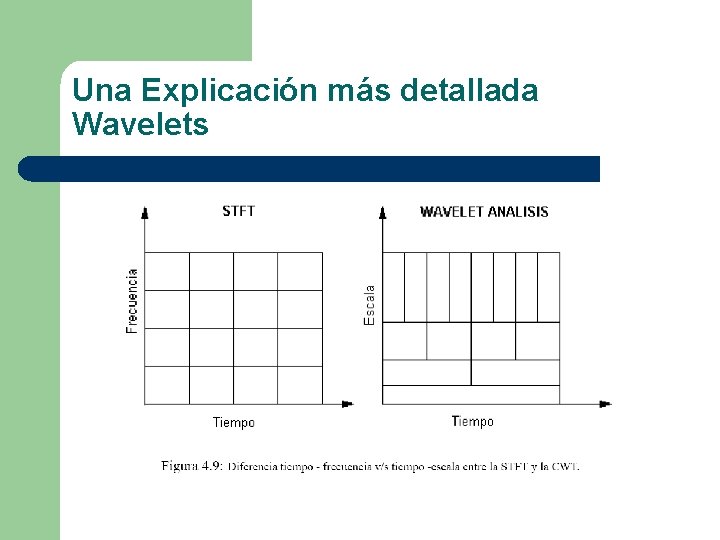
Una Explicación más detallada Wavelets l La diferencia principal entre la CWT y la STFT, es que la primera ocupa ventanas de corta duración para altas frecuencias y ventanas de larga duración para bajas frecuencias mientras que la STFT ocupa una sola ventana con la misma duración tanto para altas frecuencias como para bajas frecuencias.

Una Explicación más detallada Wavelets

Una Explicación más detallada Wavelets l Los valores de a y b deben ser discretizados, por lo que es necesario hallar una transformada discreta

Una Explicación más detallada Wavelets

Ejemplo de compresión l l l Las wavelets NO comprimen por si mismas, pero son las componentes de la imagen. Tenemos una imagen de grises con los valores (1, 3, 7, 9, 8, 8, 6, 2) donde 0 es blanco y 15 es negro, de modo que podria describir un objeto gris sobre un fondo claro Podemos calcular el promedio de pixeles adyacentes obteniendo (2, 8, 8, 4), que mantendria el concepto de la imagen suavizado, de esta forma se realizaría compresión, obteniendo (2, 2, 8, 8, 4, 4) que sería un degradé de la imagen original. Si queremos tener una mayor resolución, debemos tener mas información, en este caso (-1, 0, 2) con lo que obtendriamos la imagen original. Si hacemos esto no obtenemos compresión alguna, pero ya descompusimos la imagen en un “fondo” de baja resolución y otra parte de mayor resolución, de modo que en una imagen real, donde las zonas son suaves, la información del detalle, será en su mayoría 0

Compresión - Wavelets l Una propiedad fascinante de las wavelets es que eligen automáticamente las mismas características que nuestros ojos. Los coeficientes de las wavelets quedan aún tras la cuantización corresponden a píxeles que son muy distintos a sus vecinos, en el borde de los objetos de una imagen. Por tanto, las wavelets recrean una imagen principalmente trazando bordes, que es exactamente lo que hacen los humanos cuando esbozan un dibujo.

Pertinencia Wavelets-Fourier l Una señal de la forma de una onda de diente de sierra. La intensidad de la señal sube continuamente con el tiempo, y entonces baja abruptamente antes de comenzar otra rampa de nuevo. Esta forma simple puede ser representada como una suma de wavelets. Las wavelets de escala gruesa duran a grandes rasgos la duración de la rampa, la parte suave de subida de la onda, mientras que las wavelets de escala fina capturan el salto en la mitad. Ambas transformadas de Fourier y de wavelet nos muestran una descomposición de la señal en bloques de construcción únicos (sinusoides y wavelets). Donde difieren es en su eficiencia para un trabajo en concreto. La señal de diente de sierra, muestreada a 256 observaciones por segundo, es compactamente representada por 16 wavelets. Por otro lado, un análisis de Fourier de la misma señal de diente de sierra necesitaría 256 sinusoides completas debido a la dificultad de la técnica para representar la discontinuidad en la mitad de la señal (Bruce, 1996).

Pertinencia Wavelets-Fourier l La eficiencia de las wavelets en representar señales e imágenes con discontinuidades es una clave para su utilidad con problemas como compresión de datos y eliminación de ruido. Singularidades y bordes, que son difíciles de discernir desde una transformada de Fourier, aparecen claramente en la transformada de wavelet. Por tanto, el análisis de wavelet puede ayudar a un ingeniero a identificar más rápidamente ocurrencias importantes localizadas en una imagen.

Cálculo Matricial - Wavelets l El análisis de wavelet ha probado ser potente en facilitar ciertos tipos de problemas computacionales. El álgebra matricial es uno de estos casos. Variadas integrales y ecuaciones diferenciales, cuando son expresadas en forma digitalizada para un ordenador, pueden ser resueltas usando el álgebra matricial. Desafortunadamente, la velocidad de estas operaciones matriciales es baja, típicamente del orden de n 2 ciclos de CPU para una matriz de n x n elementos. En 1990, la idea brillante de ver las matrices como imágenes se le ocurrió a Gregory Beylkin. Cuando la "imagen" de la matriz se manda a la transformada de wavelet, es necesariamente comprimida debido al esparcimiento de la transformada. Operaciones simples, como multiplicación de matrices, se convierten en un trabajo rápido en el "dominio wavelet" porque las operaciones pueden ser hechas directamente en los coeficientes wavelet. La transformada inversa es entonces aplicada para retornar al dominio del problema original, dando una solución aproximada a la ecuación diferencial o integral. Esta solución aproximada notablemente buena requiere sólo una fracción del esfuerzo computacional necesario para la solución exacta (Bruce, 1996).

Limpiado de Señal - Wavelets l l Dejar a las señales e imágenes sin ruido es a menudo mucho más fácil en el dominio de wavelet que en el dominio original. Con wavelets, el ruido puede ser eliminado de un gran número de tipos de señal, incluyendo aquellas con saltos, picos y otras ocurrencias no demasiado suaves. La eliminación de ruido por wavelets es superior a las técnicas tradicionales, que eliminan el ruido por medio de filtrados paso bajo, emborronando las zonas abruptas de la señal. El procedimiento trabaja tomando la transformada de wavelet de la señal, poniendo a cero los coeficientes por debajo de un cierto límite e invirtiendo la transformada para reconstruir la señal original menos sin el ruido. El proceso de filtrar los coeficientes es bastante parecido a mantener sólo los coeficientes más importantes en los algoritmos de compresión de datos

Referencias l l l Procesamiento digital de señales acústicas usando wavelets, Pablo Faundez Técnicas de compresión de la Información digital, Martín Nieves Baena Wavelets: ver el bosque y los árboles, Dana Mackenzie