Introduccin a las Matemticas Financieras Inters compuesto Capitalizacin

Introducción a las Matemáticas Financieras Interés compuesto

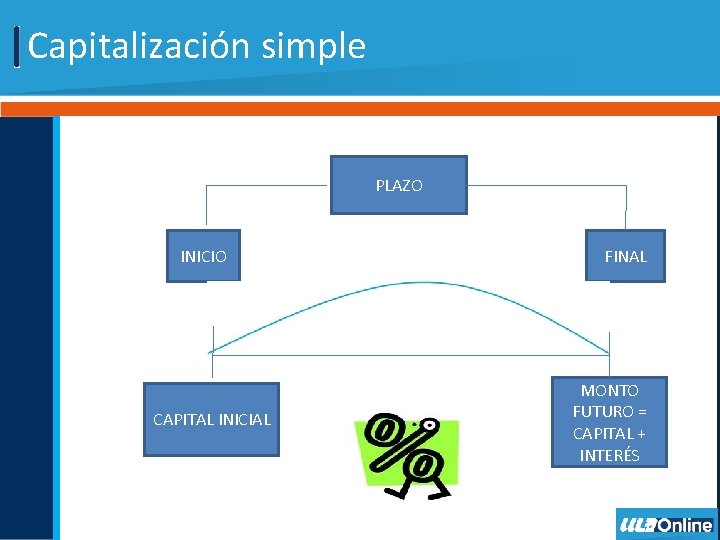
Capitalización simple PLAZO INICIO CAPITAL INICIAL FINAL MONTO FUTURO = CAPITAL + INTERÉS

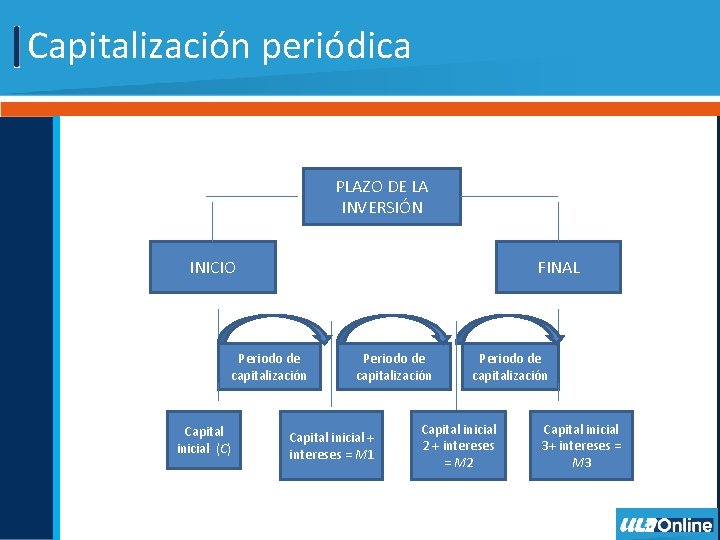
Capitalización periódica PLAZO DE LA INVERSIÓN INICIO FINAL Periodo de capitalización Capital inicial (C) Periodo de capitalización Capital inicial + intereses = M 1 Periodo de capitalización Capital inicial 2 + intereses = M 2 Capital inicial 3+ intereses = M 3

Interés compuesto • Los intereses obtenidos en cada periodo se agregan al capital para formar un nuevo capital a invertir o tomar en préstamo. • Esta es la base del interés compuesto.

Elementos • Los conceptos de Monto, Capital, Plazo, son los mismos que se utilizan en el interés simple. La diferencia radica en la tasa de interés, ya que en el interés compuesto, la tasa se divide entre el número de periodos de capitalización. • El plazo debe estar especificado en las mismas unidades que la tasa de interés.

Tasas de interés Tasa nominal • Es la tasa de interés que rige durante todo el plazo de la inversión. Tasa periódica • Es la tasa con la que se calculan los intereses en cada periodo. • Se obtiene dividiendo la tasa nominal entre el número de periodos que se capitaliza en el año.

Modelo de interés compuesto Para determinar el monto se utiliza la fórmula: Donde: M = Monto futuro C = Capital inicial i = tasa nominal i/p = tasa periódica n = plazo (en años) np = número de periodos

Ejemplo 1. Monto final Determine el importe de la cantidad acumulada en una cuenta de ahorros, si se depositan $200, 000 durante 3 años, a una tasa de interés de 12% capitalizable mensualmente. . Datos C = 200, 000 i = 0. 12 anual i/p = 0. 01 mensual np = 36 meses M= ? Al finalizar los 3 años, se tendrán acumulados: $286, 153. 76

Ejemplo 2. Capital inicial Determine el importe que se tomó en préstamo, si en año y • Al finalizar los 3 años, se tendrán acumulados: medio se pagaron $75, 879, a una tasa de 15. 5% capitalizable $286, 153. 76 bimestralmente. Datos M = 75, 879 i = 0. 155 anual i/p = 0. 0258 bimestral np = 9 bimestres C=? Fórmula El préstamo fue por $60, 317. 10 Procedimiento

Ejemplo 3. Tiempo Determine en cuántos trimestres se ahorrarán $100, 000, si se depositan el día de hoy $20, 000 y el banco nos ofrece abonar una tasa de 4. 5% capitalizable trimestralmente. Datos C = 20, 000 M= 100, 000 i = 0. 045 i/p = 0. 01125 np = ? Procedimiento Fórmula Se requieren 145 trimestres

Ejemplo 4. Tasa de interés Determine, a qué tasa nominal capitalizable cada mes se tomó en préstamo la cantidad de $20, 000 durante dos años, si al final del plazo se liquidaron $25, 500? Datos C = 20, 000 M = 25, 500 np = 24 meses p =12 i=? Fórmula Procedimiento La tasa nominal es de 2. 21%

Fuente consultada • Flórez, J. A. (2011). Matemáticas financieras empresariales (2ª. ed. ). Colombia: Ecoe Ediciones. • Meza, J. (2011). Matemáticas Financieras Aplicadas (4ª ed. ). Colombia: Ecoe Ediciones. • Villalobos, J. (2012). Matemáticas Financieras (4ª ed. ). México: Pearson.