Introduccin a la GEOMETRIA ANALITICA Prof Chvez Geometra

Introducción a la GEOMETRIA ANALITICA Prof. Chávez

Geometría Euclidiana Geometría Cartesiana Geometría Sintética Geometría Analítica

EUCLIDES Nació alrededor de 325 AC Murió alrededor de 265 AC en Alejandría, Egipto. Autor de trece volúmenes de ELEMENTOS. Los seis primeros contienen una sistematización del conocimiento de Geometría Plana básica de su época. Se convierten en el paradigma de exposición científica.

RENE DESCARTES Nació el 31 de marzo de 1596 en Francia Murió el 11 de febrero de 1650 en Suecia. Creador, junto con Fermat, del METODO DE LAS COORDENADAS que transforma problemas geométricos en problemas algebraicos

Plano Euclidiano Lugares geométricos Plano Cartesiano Ecuaciones

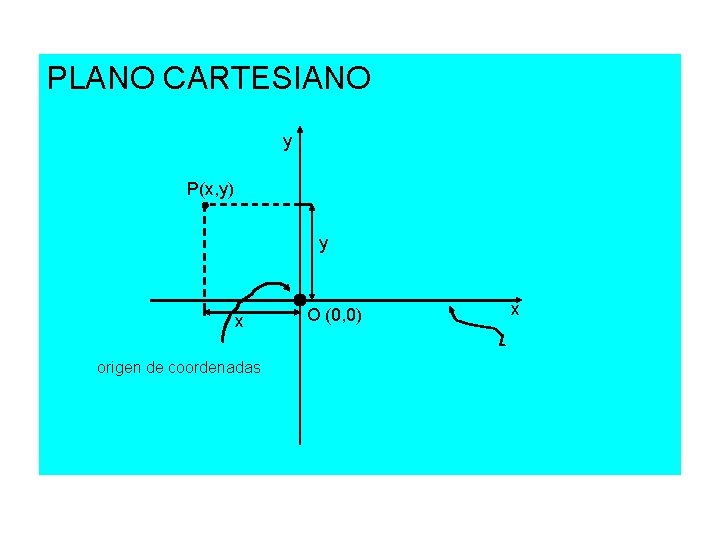
PLANO CARTESIANO y P(x, y) y x origen de coordenadas O (0, 0) x

Geometría Sintética Dos puntos determinan una recta. Geometría Analítica Ecuación de la recta

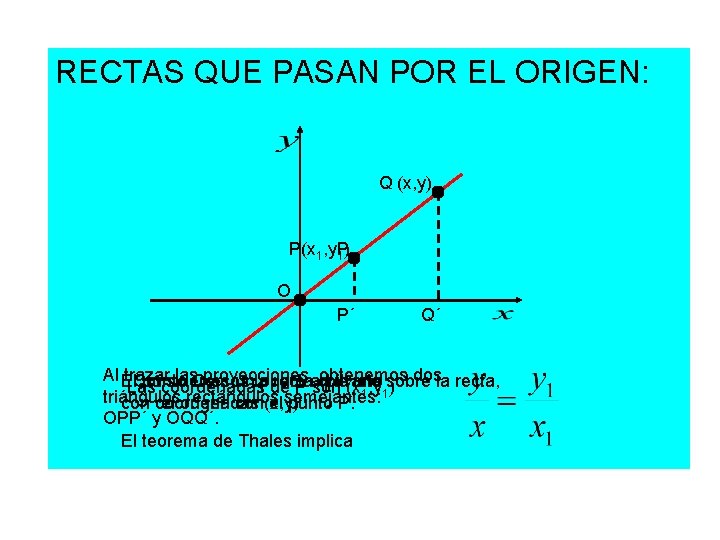
RECTAS QUE PASAN POR EL ORIGEN: Q (x, y) P(x 1, y 1 P) O P´ Q´ Al El trazar las. Qproyecciones, obtenemos dosla recta, Consideremos punto es unlapunto recta que sobre Las coordenadas de P arbitrario son (xune , y ) 1 1 triángulos rectángulos con coordenadas el origen con(x, y) el semejantes: punto P. OPP´ y OQQ´. El teorema de Thales implica

Notemos que la expresión tiene sentido siempre cuando De ser así, llamamos, como se acostumbra, pendiente. Despejamos y tenemos que es la ecuación de la recta que pasa por el origen y por el punto

Decir que es la ecuación de la recta que pasa por el origen y por el punto significa que los puntos de esa recta son precisamente aquellos que tienen la forma

PREGUNTA ¿ Cuál es la ecuación de la recta que pasa por el origen y por el punto cuando ? ¿Cuál es esta recta?

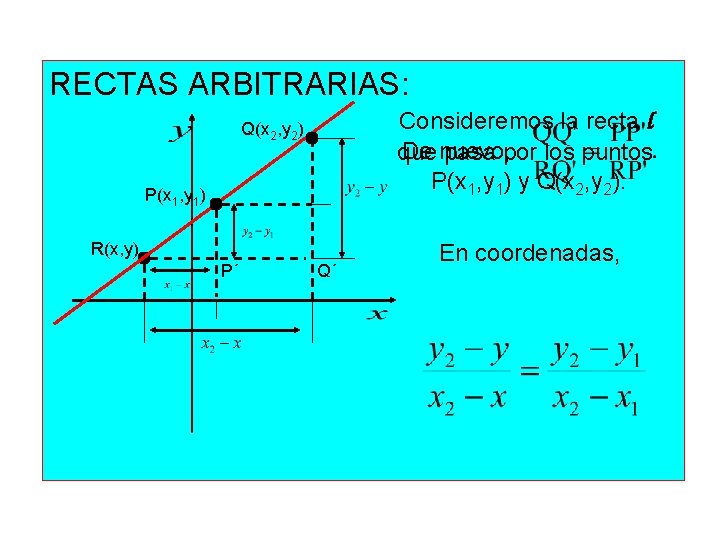
RECTAS ARBITRARIAS: Consideremos la recta l De nuevo, que pasa por los puntos P(x 1, y 1) y Q(x 2, y 2) P(x 1, y 1) R(x, y) P´ Q´ En coordenadas,

Como en el caso de las rectas que pasan por el origen, la expresión tiene sentido siempre cuando

Si , llamamos como antes pendiente de la recta a Despejamos para obtener la ecuación de la recta que pasa por los puntos y

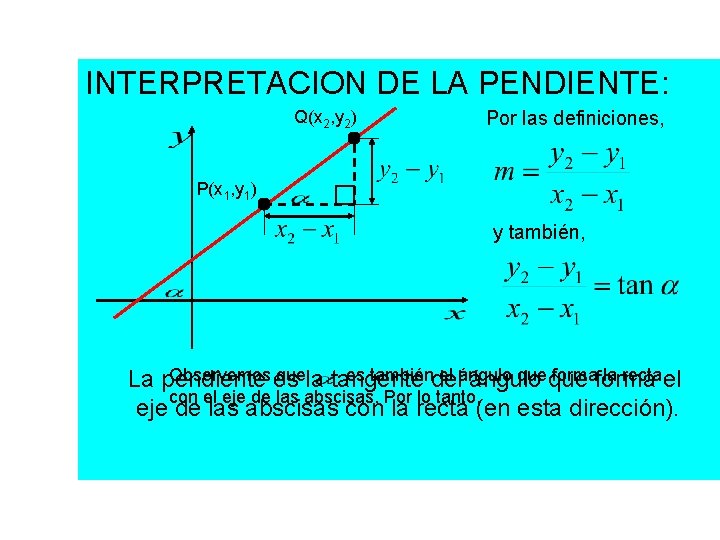
INTERPRETACION DE LA PENDIENTE: Q(x 2, y 2) Por las definiciones, P(x 1, y 1) y también, Observemos es quela tangente es tambiéndel el ángulo que forma la recta el La pendiente ángulo con el eje de las abscisas. Por lo tanto, eje de las abscisas con la recta (en esta dirección).

Geometría Analítica: Geometría Sintética. Rectas secantes. Geometría Analítica Si. Si P(x 0, y 0) está sobre la recta Entonces l 1 de ecuación l 1 Condiciones sobre y sobre la recta l 2 de la pendiente. P(x 0, y 0) Rectas secantes. ecuación es solución del sistema l 2

Geometría Analítica: Rectas secantes. Resolvamos el sistema Cuando remplazamos el valor de y de la segunda ecuación en la primera obtenemos Operamos y agrupamos

Geometría Analítica: Rectas secantes. La ecuación tiene solución siempre que CONSECUENCIA Dos rectas con pendientes distintas siempre se intersectan. POR CONSIGUIENTE…

Geometría Sintética Rectas Paralelas son aquellas que no se intersectan. Geometría Analítica Tienen la misma pendiente.

Geometría Sintética Geometría Analítica Teorema de Pitágoras Distancia entre dos puntos

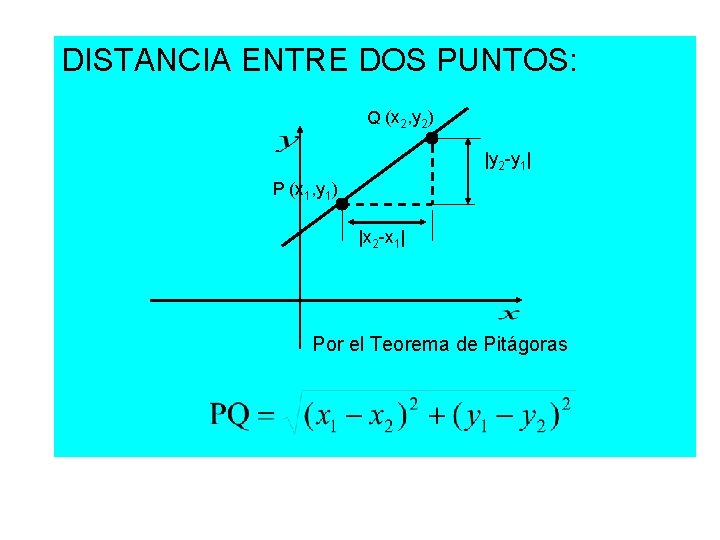
DISTANCIA ENTRE DOS PUNTOS: Q (x 2, y 2) |y 2 -y 1| P (x 1, y 1) |x 2 -x 1| Por el Teorema de Pitágoras

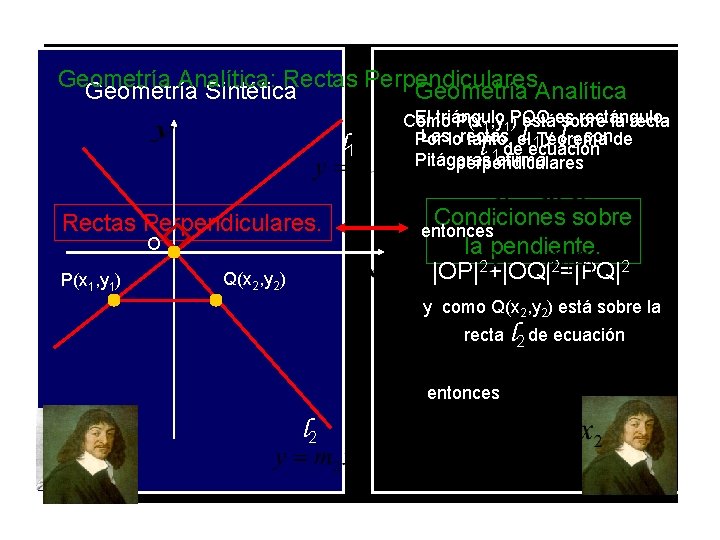
Geometría Analítica: Rectas Perpendiculares. Geometría Sintética Geometría Analítica l 1 Rectas Perpendiculares. O P(x 1, y 1) Q(x 2, y 2) El triángulo rectángulo. Como P(x 1, y 1 POQ ) estáes sobre la recta Laslorectas l ecuación y l 2 sonde Por tanto, el 1 Teorema l de 1 afirma Pitágoras perpendiculares Condiciones sobre la pendiente. |OP|2+|OQ|2=|PQ|2 entonces y como Q(x 2, y 2) está sobre la recta l 2 de ecuación entonces l 2

Geometría Analítica: Rectas perpendiculares. Como y obtenemos

Geometría Analítica: Rectas perpendiculares. De obtenemos y cuando simplificamos

Geometría Analítica: Rectas perpendiculares. Hemos mostrado que dos rectas de pendientes son perpendiculares, cuando y sólo cuando

Geometría Analítica: Algunos ejercicios. Hallar los puntos sobre el eje de las abscisas que distan 5 del punto P(2, -3) Dados P(2, 2) y Q(5, -2), hallar los puntos R sobre el eje de las abscisas tales que el ángulo es recto.

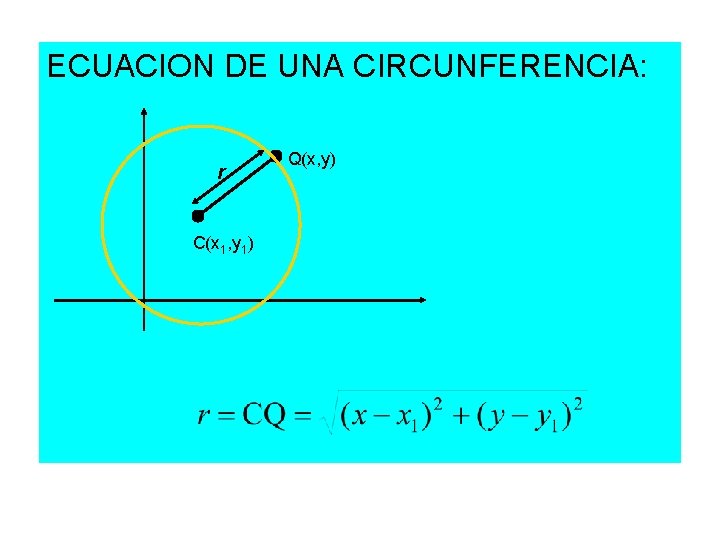
Geometría Sintética Circunferencia: Lugar geométrico de todos los puntos que equidistan de un punto dado Geometría Analítica Ecuación de la circunferencia

ECUACION DE UNA CIRCUNFERENCIA: r C(x 1, y 1) Q(x, y)