Intro to Theory of Computation LECTURE 18 Last












- Slides: 15

Intro to Theory of Computation LECTURE 18 Last time • ATM is unrecognizable • Reductions Today • Reductions • Mapping reductions Homework 7 due Homework 8 out Sofya Raskhodnikova 3/17/2016

Problems in language theory ADFA ATM decidable undecidable EDFA ECFG ETM decidable EQDFA EQCFG decidable 3/17/2016 ACFG ? undecidable EQTM ? L 18. 2

Using reductions to prove undecidability We want to prove that language L is undecidable. Idea: Use a proof by contradiction. 1. Suppose to the contrary that L is decidable. 2. Use a decider for L as a subroutine to construct a decider for ATM. 3. But ATM is undecidable. Contradiction! 3/17/2016 L 18. 3

I-clicker question (frequency: AC) To prove that ETM is undecidable A. we assumed ETM had a decider and used it to construct a decider for ATM B. we assumed ATM had a decider and used it to construct a decider for ETM C. we constructed a TM S that on input <M, w> decides whether M accepts w, assuming the existence of a TM R that decides on input <M’> whether the language of <M’> is empty D. There is more than one correct answer. E. None of the above. 3/17/2016 L 18. 4

Prove that CFLTM is undecidable Proof: Suppose to the contrary that CFLTM is decidable, and let R be a TM that decides it. We construct TM S that decides ATM. 3/17/2016 it rejects L 18. 5

Prove that EQTM is undecidable Proof: Suppose to the contrary that EQTM is decidable, and let R be a TM that decides it. We construct TM S that decides ATM. 3/17/2016 it accepts L 18. 6

Proof 2 that EQTM is undecidable Proof: Suppose to the contrary that EQTM is decidable, and let R be a TM that decides it. We construct TM S that decides ETM. What do we change? 3/17/2016 it accepts L 18. 7

Problems in language theory ADFA ATM decidable undecidable EDFA ECFG ETM decidable undecidable EQDFA EQCFG EQTM decidable 3/17/2016 ACFG ? undecidable L 18. 8

Proving undecidability and unrecognizability Mapping Reductions 3/17/2016 L 18. 9

Computable functions 3/17/2016 L 18. 10

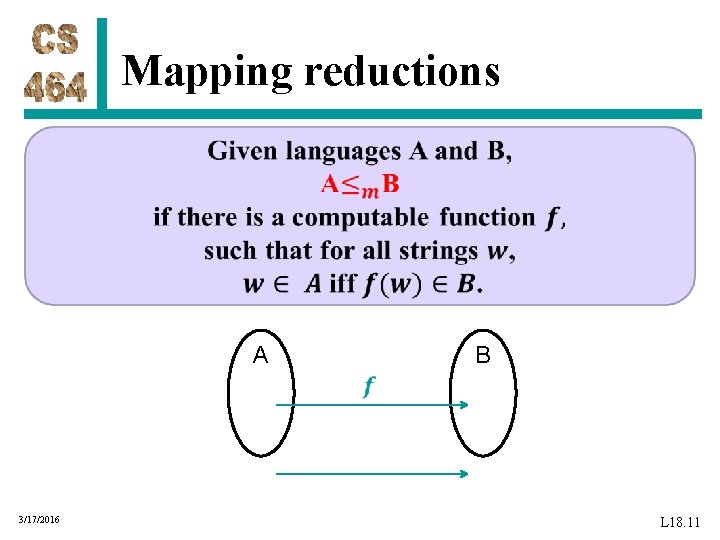
Mapping reductions A B 3/17/2016 L 18. 11

Using mapping reductions to prove decidability 3/17/2016 L 18. 12

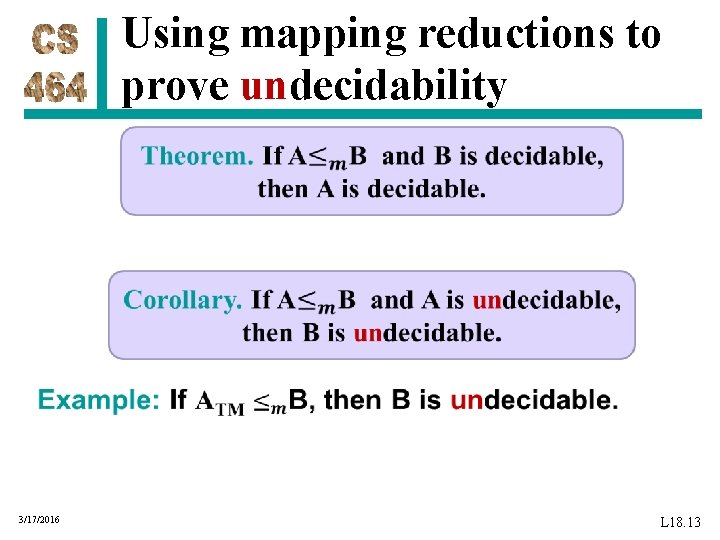
Using mapping reductions to prove undecidability 3/17/2016 L 18. 13

Using mapping reductions to prove recognizability 3/17/2016 L 18. 14

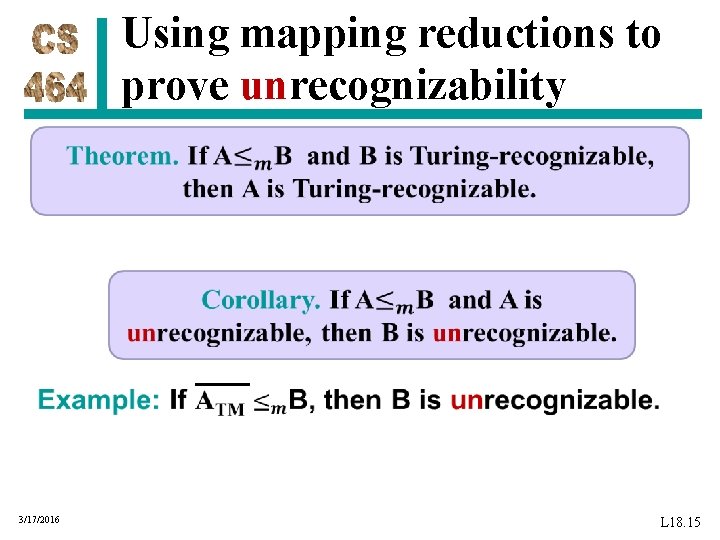
Using mapping reductions to prove unrecognizability 3/17/2016 L 18. 15