Intro to Theory of Computation LECTURE 14 Last

Intro to Theory of Computation LECTURE 14 Last time • Turing Machine Variants • Church-Turing Thesis Today • Universal TM • Decidable languages • Designing deciders Sofya Raskhodnikova 9/10/2020 Homework 5 due Homework 6 out Sofya Raskhodnikova; based on slides by Nick Hopper

The Church-Turing Thesis (1936) L is recognized by a program for some computer* ↕ L is recognized by a TM History • 23 Hilbert’s problems (1900) • stated at International Congress of Mathematicians • 10 th problem: Give a procedure for determining if a polynomial in k variables has an integral root. * The computer must be “reasonable” 9/10/2020 Sofya Raskhodnikova; based on slides by Nick Hopper L 14. 2

I-clicker problem (frequency: AC) The language corresponding to Hilbert’s 10 th problem is A. B. C. D. E. not Turing-recongnizable Turing-recognizable, but not decidable regular More than one choice above works.

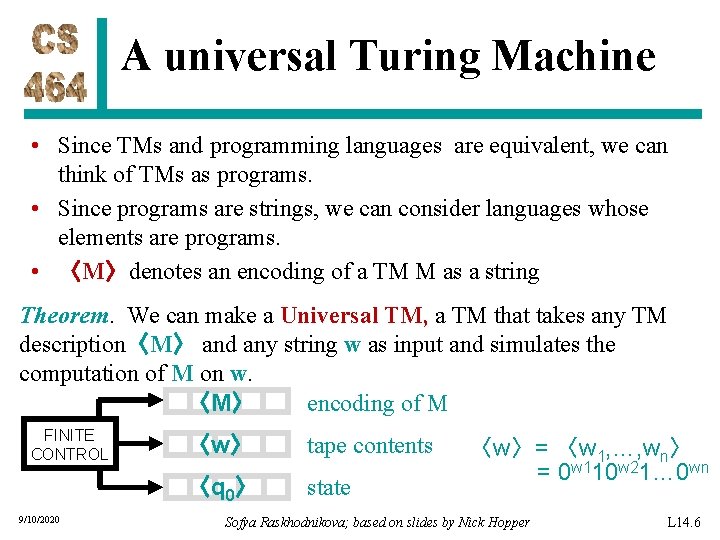
A universal Turing Machine • Since TMs and programming languages are equivalent, we can think of TMs as programs. • Since programs are strings, we can consider languages whose elements are programs. 9/10/2020 Sofya Raskhodnikova; based on slides by Nick Hopper L 14. 4

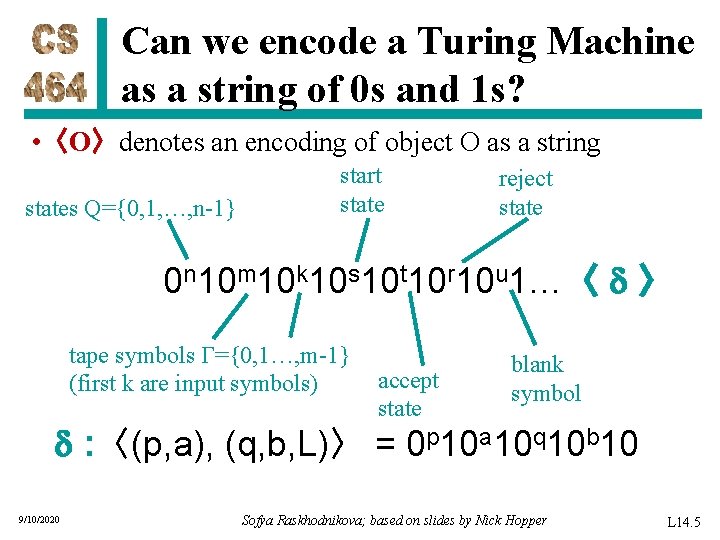
Can we encode a Turing Machine as a string of 0 s and 1 s? • 〈O〉denotes an encoding of object O as a string states Q={0, 1, …, n-1} start state reject state 0 n 10 m 10 k 10 s 10 t 10 r 10 u 1…〈 〉 tape symbols Γ={0, 1…, m-1} (first k are input symbols) 9/10/2020 blank accept symbol state : 〈(p, a), (q, b, L)〉 = 0 p 10 a 10 q 10 b 10 Sofya Raskhodnikova; based on slides by Nick Hopper L 14. 5

A universal Turing Machine • Since TMs and programming languages are equivalent, we can think of TMs as programs. • Since programs are strings, we can consider languages whose elements are programs. • 〈M〉denotes an encoding of a TM M as a string Theorem. We can make a Universal TM, a TM that takes any TM description〈M〉 and any string w as input and simulates the computation of M on w. encoding of M 〈M〉 FINITE CONTROL 9/10/2020 〈w〉 tape contents 〈q 0〉 state 〈w〉= 〈w 1, …, wn〉 = 0 w 110 w 21… 0 wn Sofya Raskhodnikova; based on slides by Nick Hopper L 14. 6

Encodings of DFAs, NFAs, CFGs, etc • Similarly, we can encode DFAs, NFAs, regular expressions, PDAs, CFGs, etc into strings of 0 s and 1 s. • We can define the following languages: ADFA = { 〈D, w〉 | D is a DFA that accepts string w } ANFA = { 〈N, w〉 | N is an NFA that accepts string w } ACFG = { 〈G, w〉 | G is a CFG that generates string w } 9/10/2020 Sofya Raskhodnikova; based on slides by Nick Hopper L 14. 7

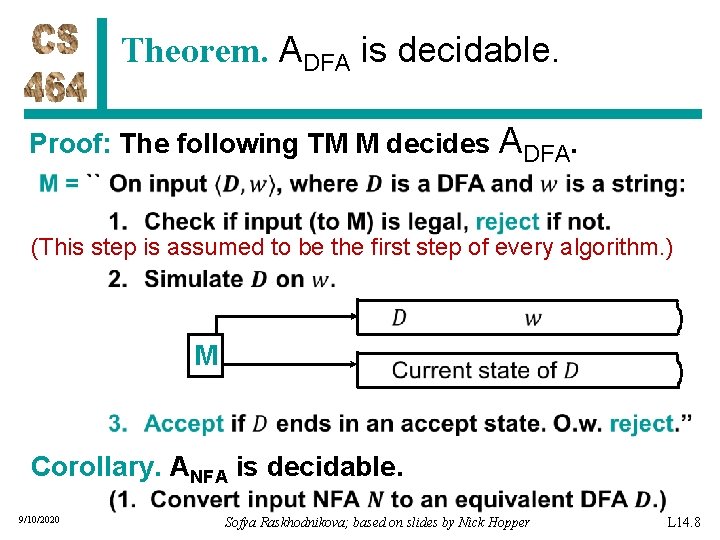
Theorem. ADFA is decidable. Proof: The following TM M decides ADFA. (This step is assumed to be the first step of every algorithm. ) M Corollary. ANFA is decidable. 9/10/2020 Sofya Raskhodnikova; based on slides by Nick Hopper L 14. 8

Theorem. ACFG is decidable. ACFG = { 〈G, w〉 | G is a CFG that generates string w } 9/10/2020 Sofya Raskhodnikova; based on slides by Nick Hopper L 14. 9

Chomsky Normal Form for CFGs 9/10/2020 Sofya Raskhodnikova; based on slides by Nick Hopper L 14. 10

Chomsky Normal Form for CFGs 9/10/2020 Sofya Raskhodnikova; based on slides by Nick Hopper L 14. 11

Theorem. ACFG is decidable. ACFG = { 〈G, w〉 | G is a CFG that generates string w } Proof: The following TM M decides ACFG. 9/10/2020 Sofya Raskhodnikova; based on slides by Nick Hopper L 14. 12

Examples of decidable languages ADFA = { 〈D, w〉 | D is a DFA that accepts string w } ANFA = { 〈N, w〉 | N is an NFA that accepts string w } ACFG = { 〈G, w〉 | G is a CFG that generates string w } 9/10/2020 Sofya Raskhodnikova; based on slides by Nick Hopper L 14. 13

More decidable languages EDFA = { 〈D〉 | D is a DFA that recognizes the empty language } ECFG = { 〈G〉 | G is a CFG that generates the empty language} 9/10/2020 Sofya Raskhodnikova; based on slides by Nick Hopper L 14. 14

Theorem. EDFA is decidable. Proof: The following TM M decides EDFA. 1. Use BFS to determine if an accepting state of D is reachable from its start state. 2. Accept if not. O. w. reject. ’’ 9/10/2020 Sofya Raskhodnikova; based on slides by Nick Hopper L 14. 15

Theorem. EQDFA is decidable. Proof: The following TM M decides EQDFA. 9/10/2020 (on the board) Sofya Raskhodnikova; based on slides by Nick Hopper L 14. 16

Theorem. ECFG is decidable. Proof: The following TM M decides ECFG. 9/10/2020 Sofya Raskhodnikova; based on slides by Nick Hopper L 14. 17

Exercises • Prove that the following language is decidable: RDFA = { 〈D, w〉 | D is a DFA that rejects string w } • Formulate the following problem as a language and prove that it is decidable: Given a PDA and a string, determine if the PDA accepts the string. APDA = { 〈P, w〉 | P is a PDA that accepts string w } Can a TM just simulate P on w, accept if it accepts and reject o. w. ? 9/10/2020 Sofya Raskhodnikova; based on slides by Nick Hopper L 14. 18

I-clicker problem (frequency: AC) A decider for APDA can, on input <P, w> A. simulate P on w, accept if it accepts and reject o. w. B. convert P to an equivalent CFG G and then run a decider for ACFG, accept if it accepts and reject o. w. C. convert P to an equivalent CFG G and then run a decider for ACFG, accept if it rejects and accept o. w. D. None of the above. E. More than one choice above works.