Intro to Sinusoids What is a sinusoid Mathematical

Intro to Sinusoids • What is a sinusoid? » Mathematical equation : Function of the time variable : Amplitude : Frequency (# cycles per sec, Hertz) : Phase Ira Fulton School of Engineering

SINUSOIDAL SIGNAL • FREQUENCY – Radians/sec – Hertz (cycles/sec) • AMPLITUDE – Magnitude • PERIOD (in sec) • PHASE Courtesy of James Mc. Clellan et al, Signal Processing First, 2003 Ira Fulton School of Engineering

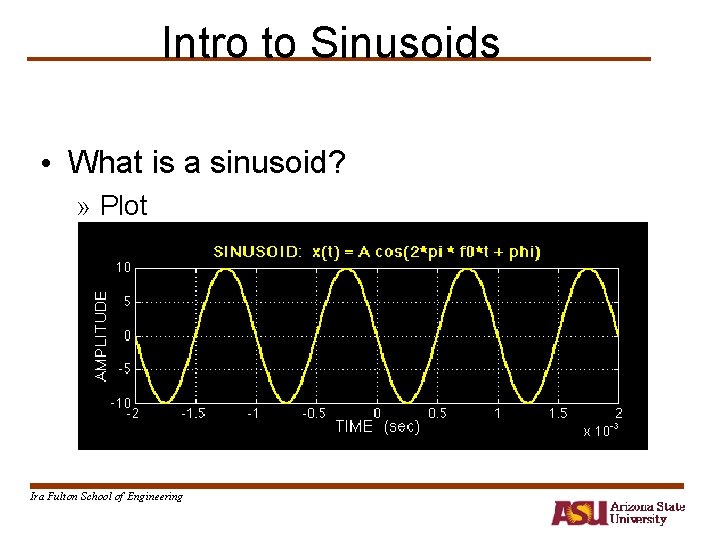
Intro to Sinusoids • What is a sinusoid? » Plot Ira Fulton School of Engineering

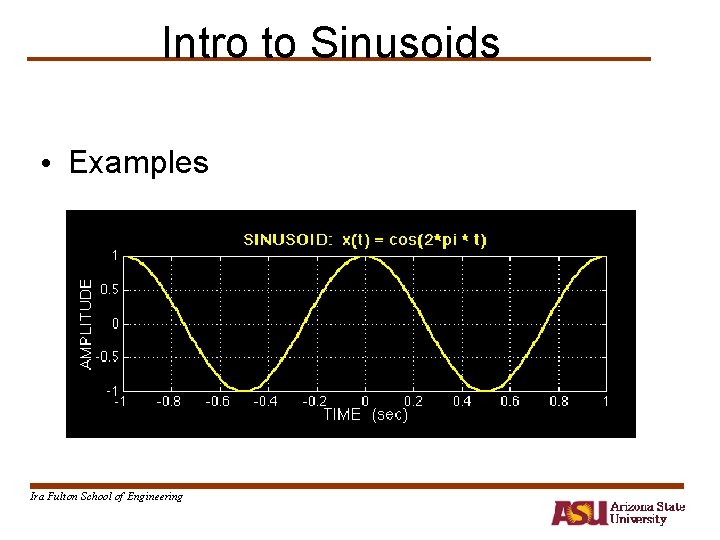
Intro to Sinusoids • Examples Ira Fulton School of Engineering

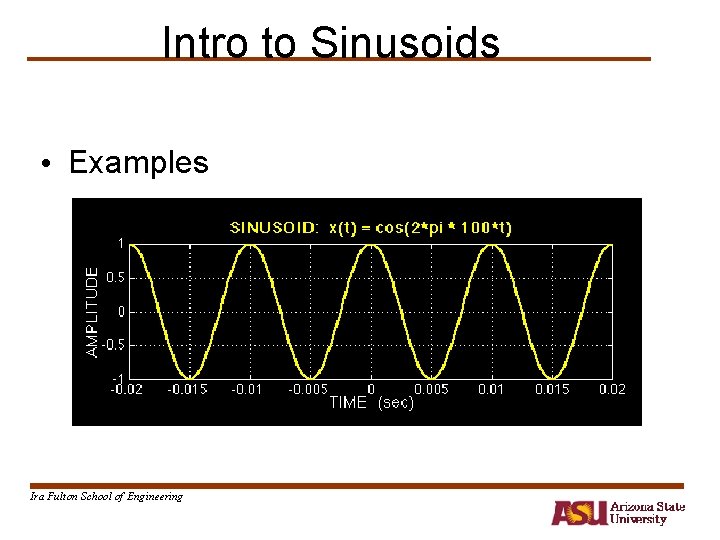
Intro to Sinusoids • Examples Ira Fulton School of Engineering

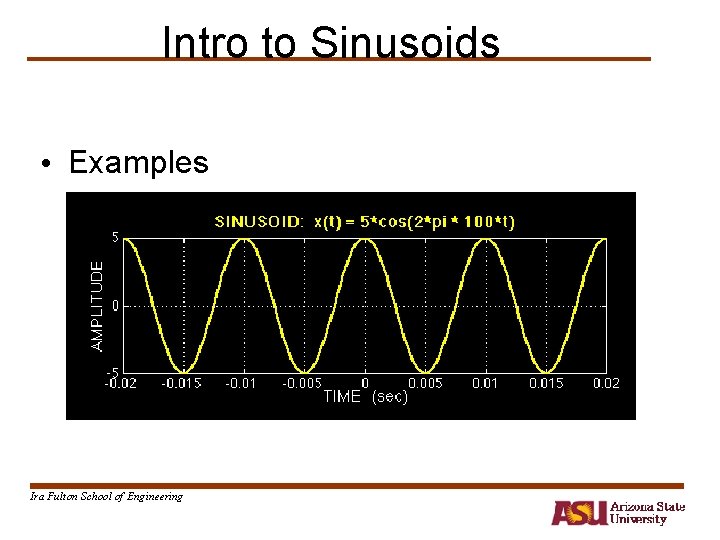
Intro to Sinusoids • Examples Ira Fulton School of Engineering

Intro to Sinusoids • How to plot a sinusoid? » Determine height » Determine zero crossings • Max height is +A » peaks oscillate: +A and -A » peaks occur when argument of cosine is a multiple of , i. e. , Ira Fulton School of Engineering

Intro to Sinusoids • Zero crossings » where plot crosses zero » located at odd multiples of , i. e. , • Note: cycles repeat (periodic function) » sufficient to determine peak and zero crossings in one cycle and then replicate cycle » Period = length of cycle = Ira Fulton School of Engineering

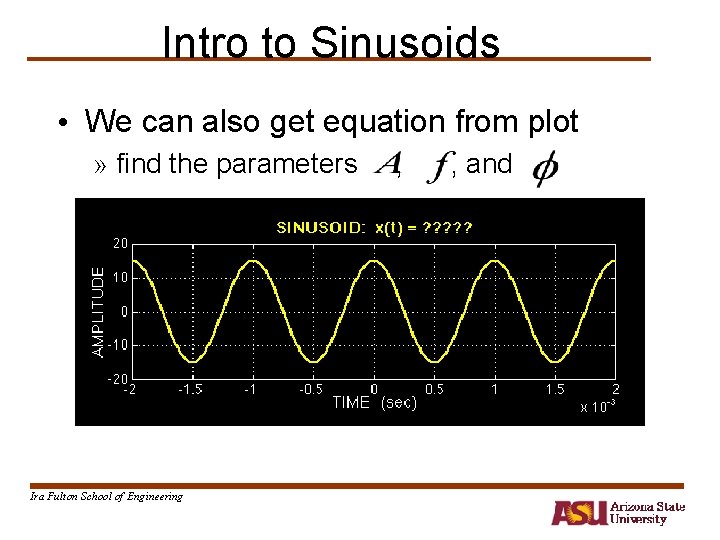
Intro to Sinusoids • We can also get equation from plot » find the parameters Ira Fulton School of Engineering , , and

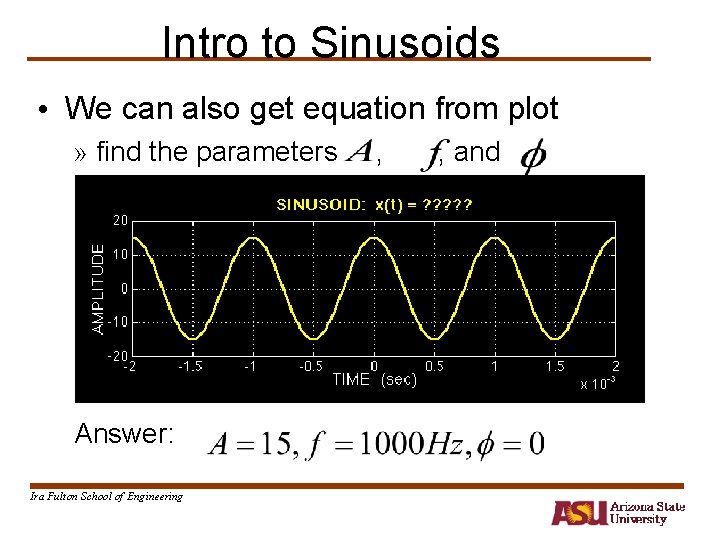
Intro to Sinusoids • We can also get equation from plot » find the parameters Answer: Ira Fulton School of Engineering , , and

Intro to Sinusoids • Procedure to get equation from plot • Find the amplitude • Find the period by measuring the time distance between positive peaks: • Find the phase by measuring the “time shift” (delay from 0) of a peak. Note: positive if peak moved to right, and negative if peak moved to left. • Then, compute Ira Fulton School of Engineering

Intro to Sinusoids • Sinusoids can be interpreted as a “rotating phasor” rotating angle • : speed of rotation (# cycles per sec) » : initial angle start point » Ira Fulton School of Engineering

Generating Signals using Sinusoids • Main reason why sinusoids are important: they are basic tools for constructing other useful and more complicated signals • A new signal can be generated by combining together different sinusoids Ira Fulton School of Engineering

Generating Signals using Sinusoids • Example: Beat Note Waveform • Beat notes generated by adding two sinusoids with nearby frequencies • They can also be generated by playing two neighboring piano keys • Mathematically: where Ira Fulton School of Engineering small.

Generating Signals using Sinusoids • Example: Beat Note Waveform • Let • Matlab Script File: beatnote. m dur = 2. 0; fs = 8000; f 1 = 220; f 2 = 180; t = 0: (1/fs): dur; x = cos(2*pi*f 1*t)+cos(2*pi*f 2*t); plot(t, x); xlabel(‘Time, t’); ylabel(‘Beat Signal’); sound(x, fs); Ira Fulton School of Engineering

Generating Signals using Sinusoids • Example: Beat Note Waveform • Let • Matlab Function: beat. m function [x, t] = beat(f 0, d, dur); fs = 8000; f 1 = f 0+d; f 2 = f 0 -d; t = 0: (1/fs): dur; x = cos(2*pi*f 1*t)+cos(2*pi*f 2*t); Ira Fulton School of Engineering

Matlab Functions • Example: Beat Note Waveform • Let • Matlab Script File using Function beat. m [x, t] = beat(200, 20, 1); plot(t, x); xlabel(‘Time, t’); ylabel(‘Beat Signal’); sound(x, fs); Ira Fulton School of Engineering

Generating Signals using Sinusoids • A new signal can be generated by combining together different sinusoids • Periodic signals obtained when frequencies are integer multiples of : where is called harmonic frequency of and is called the fundamental frequency. Ira Fulton School of Engineering

Generating Signals using Sinusoids • A new periodic signal can be generated by combining together sinusoids having harmonically related frequencies • Period = length of one cycle = Ira Fulton School of Engineering

PERIODIC SIGNALS • Repeat every T secs – Definition – Example: – Speech can be “quasi-periodic” Courtesy of James Mc. Clellan et al, Signal Processing First, 2003 Ira Fulton School of Engineering

Generating Signals using Sinusoids • Example: Square Wave • For N =1: Ira Fulton School of Engineering

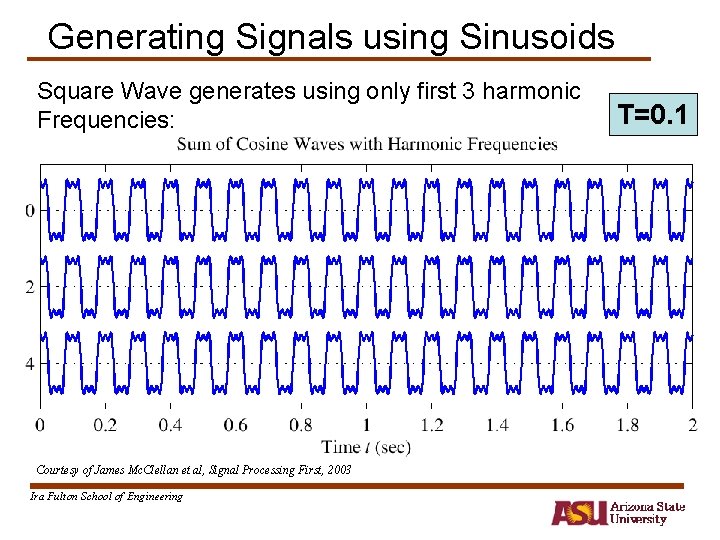
Generating Signals using Sinusoids Square Wave generates using only first 3 harmonic Frequencies: Courtesy of James Mc. Clellan et al, Signal Processing First, 2003 Ira Fulton School of Engineering T=0. 1

Generating Signals using Sinusoids • Example: Square Wave • Matlab Function square. m function [x, t] = square(f 0, N, dur); fs = 8000; t = 0: 1/fs: dur; x = zeros(1, length(t)); for m = 0: N x = x + (8/((2*m+1)*pi))*cos(2*pi*(2*m+1)*f 0*t- pi/2); end • Generate and plot square waves with = 25 Hz, dur = 0. 12 sec, and N=1, 2, 3, 25 Ira Fulton School of Engineering

Generating Signals using Sinusoids • Example: Synthetic Vowel • Generated signal approximates the waveform produced by a man speaking the sound “ah”. Ira Fulton School of Engineering

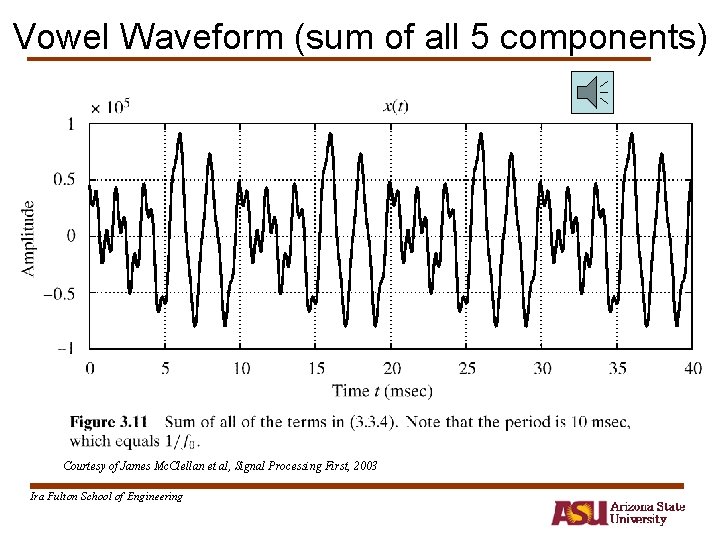
Vowel Waveform (sum of all 5 components) Courtesy of James Mc. Clellan et al, Signal Processing First, 2003 Ira Fulton School of Engineering

Generating Signals using Sinusoids • Example: Synthetic Vowel • Matlab Script File dur = 1; f = 100; fs = 8000; t = 0: 1/fs: dur; x = 12226 * cos(2*pi*2*f*t + 1. 508); x = x + 29416 * cos(2*pi*4*f*t + 1. 876); x = x + 48836 * cos(2*pi*5*f*t - 0. 185); x = x + 13621 * cos(2*pi*16*f*t - 1. 449); x = x + 4723 * cos(2*pi*17*f*t); plot(t, x); xlabel(‘Time, t’); ylabel(‘Vowel’) sound(x, fs) Ira Fulton School of Engineering

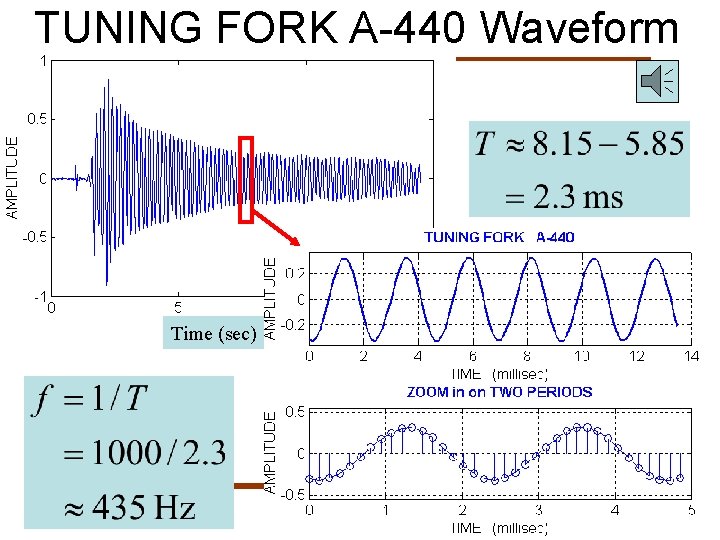
TUNING FORK EXAMPLE • • “A” is at 440 Hertz (Hz) Waveform is a SINUSOIDAL SIGNAL Computer plot looks like a sine wave This should be the mathematical formula: Courtesy of James Mc. Clellan et al, Signal Processing First, 2003 Ira Fulton School of Engineering

TUNING FORK A-440 Waveform Time (sec) Ira Fulton School of Engineering

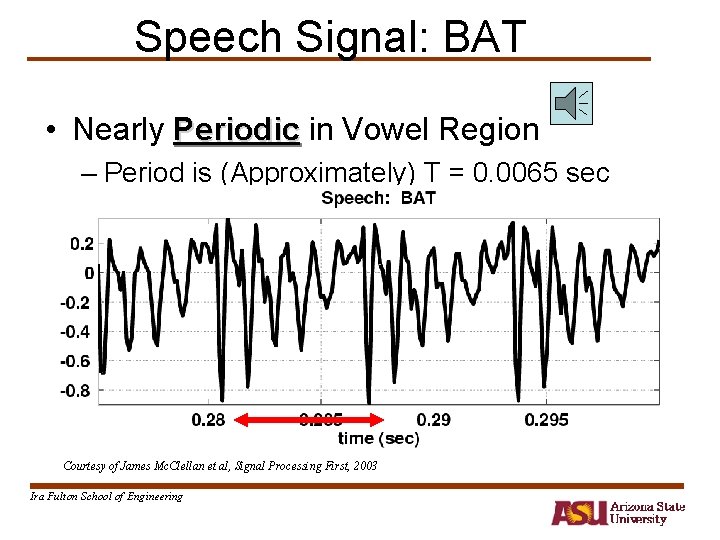
SPEECH EXAMPLE • More complicated signal (BAT. WAV) • Waveform x(t) is NOT a Sinusoid • Theory will tell us – x(t) is approximately a sum of sinusoids – FOURIER ANALYSIS • Break x(t) into its sinusoidal components – Called the FREQUENCY SPECTRUM Courtesy of James Mc. Clellan et al, Signal Processing First, 2003 Ira Fulton School of Engineering

Speech Signal: BAT • Nearly Periodic in Vowel Region – Period is (Approximately) T = 0. 0065 sec Courtesy of James Mc. Clellan et al, Signal Processing First, 2003 Ira Fulton School of Engineering

DIGITIZE the WAVEFORM • x[n] is a SAMPLED SINUSOID – A list of numbers stored in memory • Sample at 11, 025 samples per second – Called the SAMPLING RATE of the A/D – Time between samples is • 1/11025 = 90. 7 microsec • Output via D/A hardware (at Fsamp) Courtesy of James Mc. Clellan et al, Signal Processing First, 2003 Ira Fulton School of Engineering

STORING DIGITAL SOUND • x[n] is a SAMPLED SINUSOID – A list of numbers stored in memory • • CD rate is 44, 100 samples per second 16 -bit samples Stereo uses 2 channels Number of bytes for 1 minute is – 2 X (16/8) X 60 X 44100 = 10. 584 Mbytes Courtesy of James Mc. Clellan et al, Signal Processing First, 2003 Ira Fulton School of Engineering

SINES and COSINES • Always use the COSINE FORM • Sine is a special case: Courtesy of James Mc. Clellan et al, Signal Processing First, 2003 Ira Fulton School of Engineering

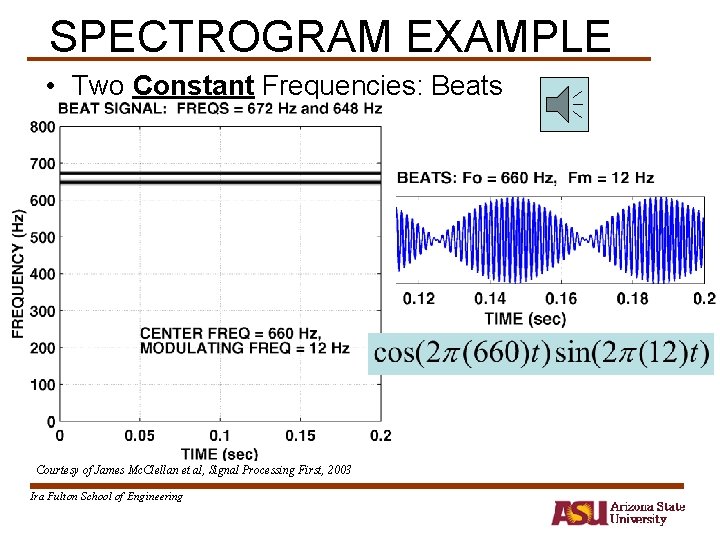
Sinusoidal Synthesis • Sinusoids with DIFFERENT Frequencies – SYNTHESIZE by Adding Sinusoids • SPECTRUM Representation – Graphical Form shows DIFFERENT Frequencies • SPECTROGRAM Tool – Shows how frequency content varies in function of time – MATLAB function is specgram. m Courtesy of James Mc. Clellan et al, Signal Processing First, 2003 Ira Fulton School of Engineering

SPECTROGRAM EXAMPLE • Two Constant Frequencies: Beats Courtesy of James Mc. Clellan et al, Signal Processing First, 2003 Ira Fulton School of Engineering

Frequency is the vertical axis Time-Varying Frequency Diagram A-440 Time is the horizontal axis Courtesy of James Mc. Clellan et al, Signal Processing First, 2003 Ira Fulton School of Engineering

Sinusoidal Synthesis: Motivation • Synthesize Complicated Signals – Musical Notes • Piano uses 3 strings for many notes • Chords: play several notes simultaneously – Human Speech • Vowels have dominant frequencies • Application: computer generated speech – Can all signals be generated this way? • Sum of sinusoids? Courtesy of James Mc. Clellan et al, Signal Processing First, 2003 Ira Fulton School of Engineering

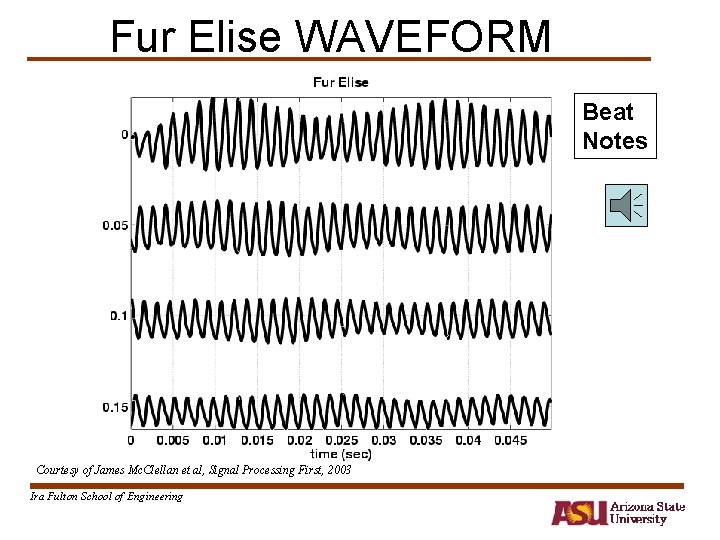
Fur Elise WAVEFORM Beat Notes Courtesy of James Mc. Clellan et al, Signal Processing First, 2003 Ira Fulton School of Engineering

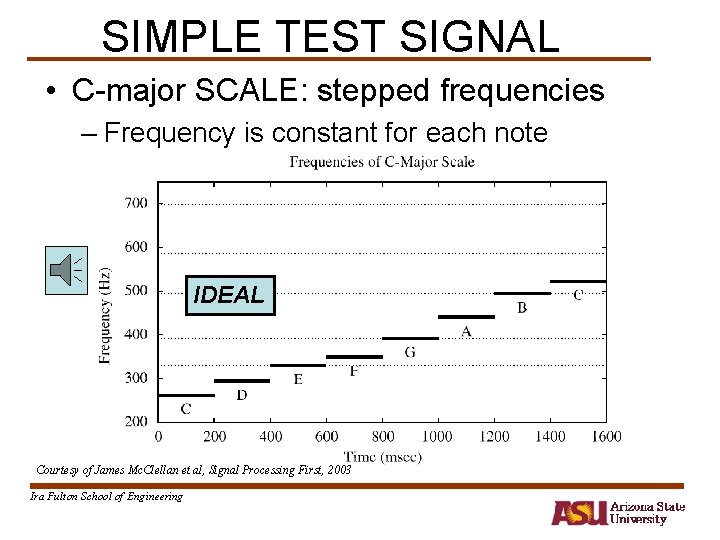
SIMPLE TEST SIGNAL • C-major SCALE: stepped frequencies – Frequency is constant for each note IDEAL Courtesy of James Mc. Clellan et al, Signal Processing First, 2003 Ira Fulton School of Engineering

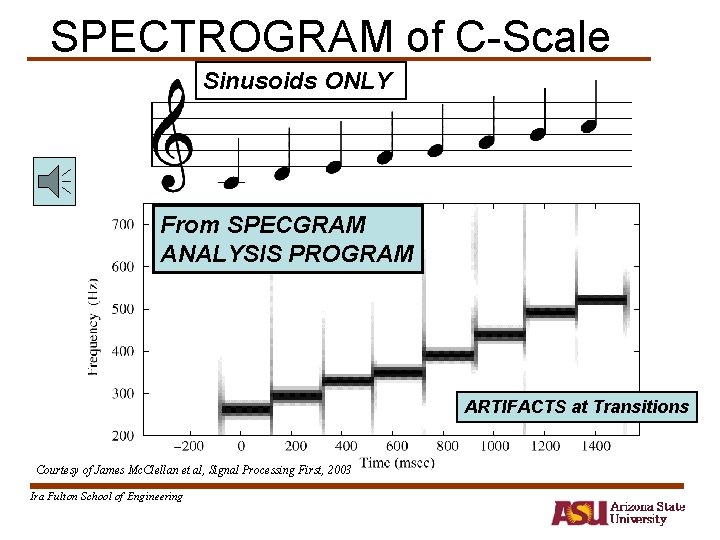
SPECTROGRAM of C-Scale Sinusoids ONLY From SPECGRAM ANALYSIS PROGRAM ARTIFACTS at Transitions Courtesy of James Mc. Clellan et al, Signal Processing First, 2003 Ira Fulton School of Engineering

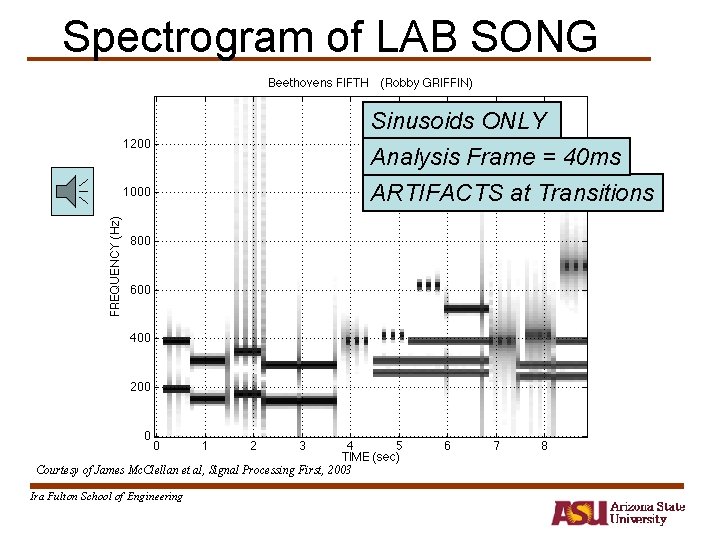
Spectrogram of LAB SONG Sinusoids ONLY Analysis Frame = 40 ms ARTIFACTS at Transitions Courtesy of James Mc. Clellan et al, Signal Processing First, 2003 Ira Fulton School of Engineering

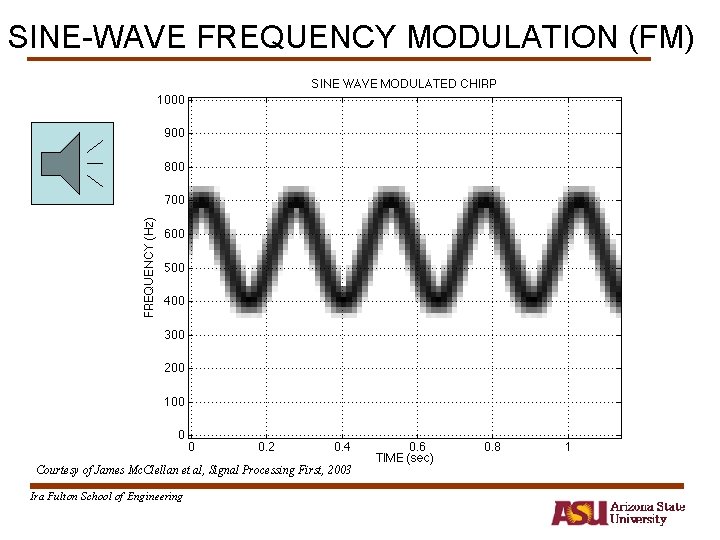
Time-Varying Frequency • Frequency can change vs. time – Continuously, not stepped • FREQUENCY MODULATION (FM) VOICE • CHIRP SIGNALS – Linear Frequency Modulation (LFM) Courtesy of James Mc. Clellan et al, Signal Processing First, 2003 Ira Fulton School of Engineering

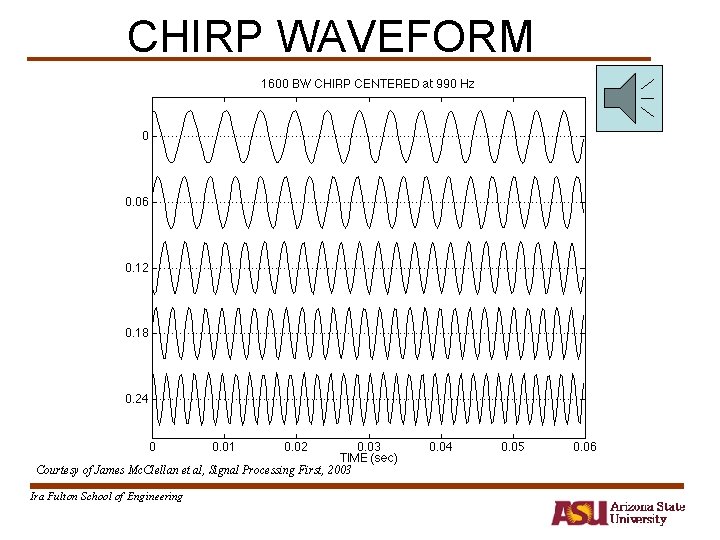
New Signal: Linear FM • Called Chirp Signals (LFM) – Quadratic phase QUADRATIC • Freq will change LINEARLY versus time – Example of Frequency Modulation (FM) – Define “instantaneous frequency” Courtesy of James Mc. Clellan et al, Signal Processing First, 2003 Ira Fulton School of Engineering

INSTANTANEOUS FREQ • Definition Derivative of the “Angle” • For Sinusoid: Makes sense Courtesy of James Mc. Clellan et al, Signal Processing First, 2003 Ira Fulton School of Engineering

INSTANTANEOUS FREQ of the Chirp • Chirp Signals have Quadratic phase • Freq will change LINEARLY versus time Courtesy of James Mc. Clellan et al, Signal Processing First, 2003 Ira Fulton School of Engineering

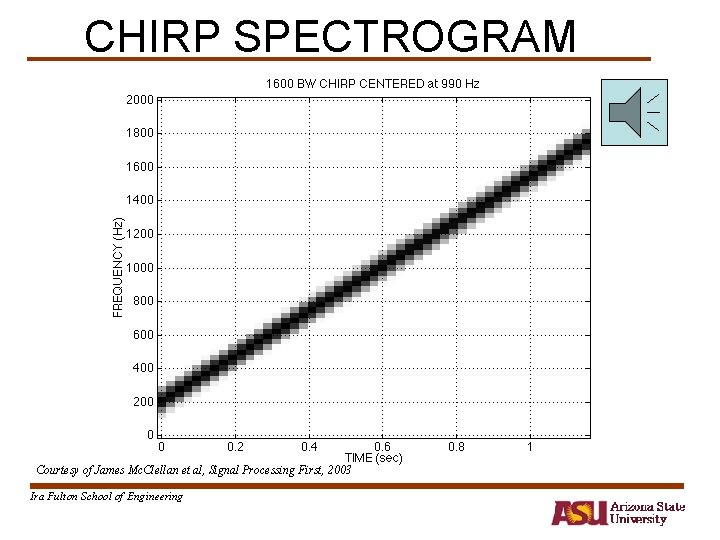
CHIRP SPECTROGRAM Courtesy of James Mc. Clellan et al, Signal Processing First, 2003 Ira Fulton School of Engineering

CHIRP WAVEFORM Courtesy of James Mc. Clellan et al, Signal Processing First, 2003 Ira Fulton School of Engineering

OTHER CHIRPS • y(t) can be anything: • y(t) could be speech or music: – FM radio broadcast Courtesy of James Mc. Clellan et al, Signal Processing First, 2003 Ira Fulton School of Engineering

SINE-WAVE FREQUENCY MODULATION (FM) Courtesy of James Mc. Clellan et al, Signal Processing First, 2003 Ira Fulton School of Engineering

Music Synthesis • Musical notes synthesized using a sinewave at a given frequency. • Musical scale is divided into 8 octaves; each octave consists of 12 notes. • Notes in each octave are related to notes in previous and next octave: – The frequency of a note is twice the frequency of the corresponding note in the previous adjacent (lower) octave. • Each octave contains 12 notes (5 black keys and 7 white) and the ratio between the frequencies of the notes is constant between successive notes: fnext note = 21/12 fprevious note Ira Fulton School of Engineering

Music - Octave • D 4 denotes D note in 4 th octave • A 4 or A-440 note (tone at 440 Hz) is usually a reference note called middle A. Ira Fulton School of Engineering

Music - Octave Ira Fulton School of Engineering

Music - Notation 4 • Musical notation shows which notes are to be played and their relative timing Ira Fulton School of Engineering

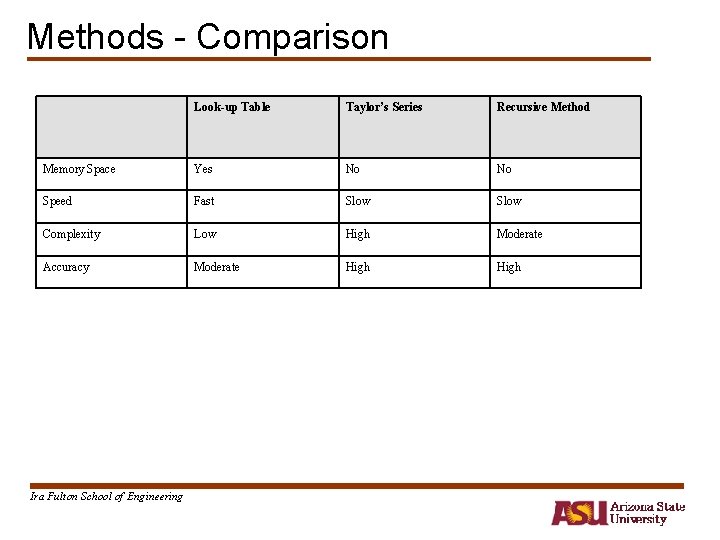
Sinewave Synthesis • Methods used – Recursive – Taylor’s Series – Look-up Table Ira Fulton School of Engineering

Recursive Method Let A = and B =n where is the angle and n the index For = 1 and n= 1 Sin(2) and cos(2) can be computed using only four multiplications and 2 addition/subtraction Sin(1) and cos(1) must first be precomputed and stored in memory Ira Fulton School of Engineering

Recursive Method – Practical Example • Generate a sine wave of frequency F = 100 Hz having a sample frequency Fs equals to 8000 samples/s. • Calculate the angle increment – Total number of samples/period = Fs/F = 80 – The angle increment = 360/80 = 4. 5 • Precompute sin(4. 5) and cos(4. 5) • Apply the recursive method Ira Fulton School of Engineering

Taylor’s Series Ira Fulton School of Engineering

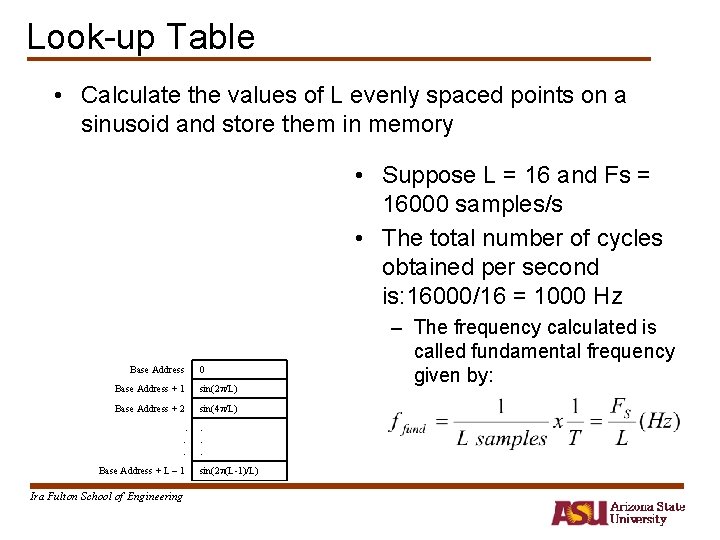
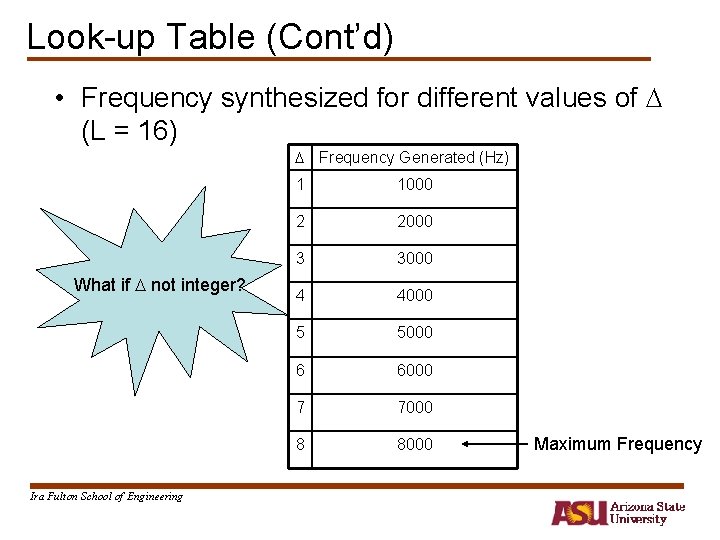
Look-up Table • Calculate the values of L evenly spaced points on a sinusoid and store them in memory • Suppose L = 16 and Fs = 16000 samples/s • The total number of cycles obtained per second is: 16000/16 = 1000 Hz Base Address 0 Base Address + 1 sin(2 /L) Base Address + 2 sin(4 /L). . . Base Address + L – 1 Ira Fulton School of Engineering . . . sin(2 (L-1)/L) – The frequency calculated is called fundamental frequency given by:

Look-up Table (Cont’d) • If the samples are not read sequentially from the look-up table (e. g. , skipping one sample), the frequency generated will be: where: Example: Suppose Fs = 16 Khz, L = 16, and = 2: Ira Fulton School of Engineering and is the lookup table increment index. The maximum value can reach is bounded by the Nyquist rate: = L/2 => fsin= Fs/2;

Look-up Table (Cont’d) • Frequency synthesized for different values of (L = 16) Frequency Generated (Hz) What if not integer? Ira Fulton School of Engineering 1 1000 2 2000 3 3000 4 4000 5 5000 6 6000 7 7000 8 8000 Maximum Frequency

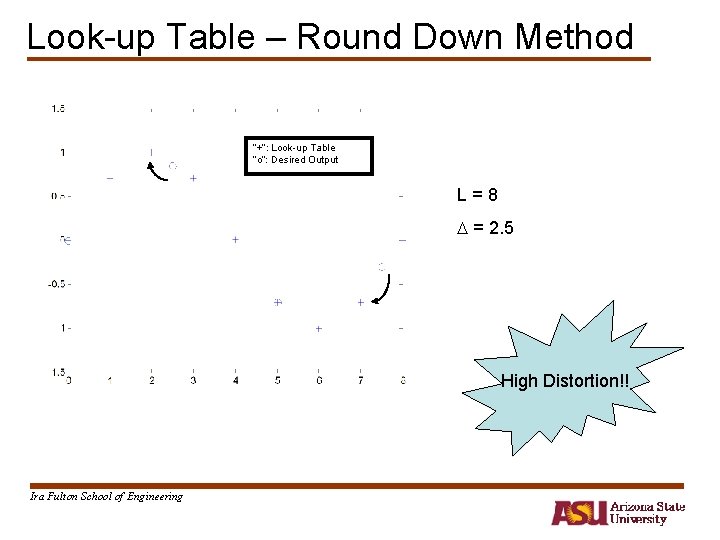
Look-up Table – Non Integer • Two Methods – Round – down – Interpolation Ira Fulton School of Engineering

Look-up Table – Round Down Method “+”: Look-up Table “o”: Desired Output L=8 = 2. 5 High Distortion!! Ira Fulton School of Engineering

Look-up Table – Interpolation Linear interpolation method used y = mx + b where: m = line slope given by (Base_address + l +1) – (Base_address + l ) Base_address is the beginning address of the lookup table. b = (Base_address + l ). x = fractional part of the pointer with 0<x<1 y = linear approximated output sample. (2, 1) Note that () denotes indirect addressing. (3, 0. 7071) Ira Fulton School of Engineering Interpolation 0. 5. (0. 7071 -1)+1 = 0. 8536

Methods - Comparison Look-up Table Taylor’s Series Recursive Method Memory Space Yes No No Speed Fast Slow Complexity Low High Moderate Accuracy Moderate High Ira Fulton School of Engineering

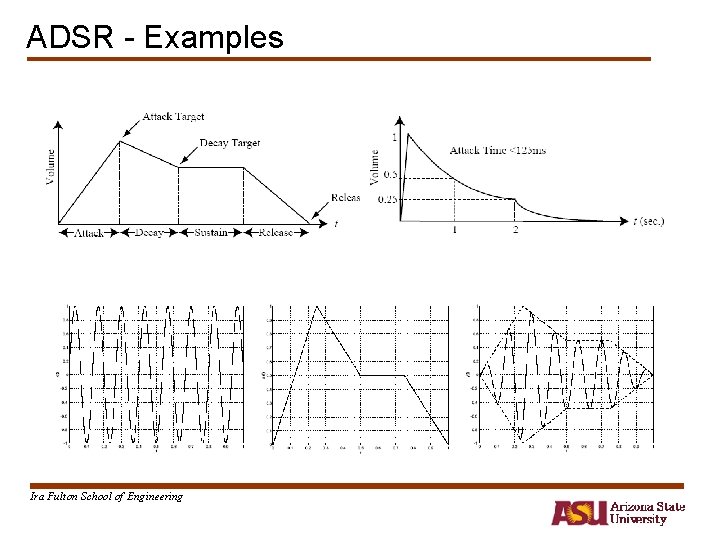
Amplitude Modulation of Tones - ADSR envelope • Smoothing may be needed since the musical note will not reach its full intensity instantaneously • Attack – Decay – Sustain- Release (ADSR) envelope - Attack time: time during which the musical note reaches its peak - Decay time: time required for the tone’s intensity to partially die away - Sustain time: time where the tone’s intensity remains unchanged - Release time: time for final attenuation Ira Fulton School of Engineering

ADSR - Examples Ira Fulton School of Engineering

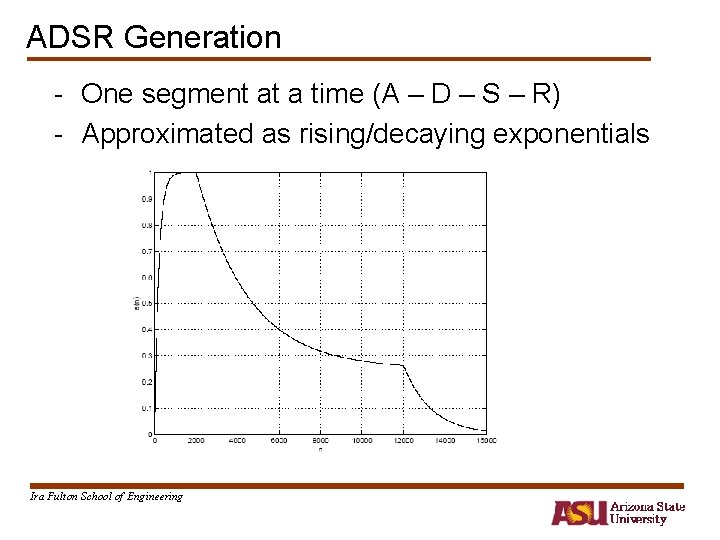
ADSR Generation - One segment at a time (A – D – S – R) - Approximated as rising/decaying exponentials Ira Fulton School of Engineering

ADSR Generation – cont’d - If Fs = 16000 samples/s and assuming a max note duration of 1 second, we need to store 16 K in memory for the ADSR envelope values, which consumes a lot of memory - An alternative to the lookup ADSR is to try to compute the values “on the fly” using the equation: ^ where g is the rise/decay rate and x(n) is the desired target value; initially x(-1)= 0. Ira Fulton School of Engineering

ADSR Generation – cont’d - The equation presented previously is a first-order IIR filter given by the following difference equation: x[n] g y[n] z-1 1 -g Ira Fulton School of Engineering

ADSR Generation – cont’d Why? ? ? IIR Filter Solve for the equation and show that the output have an exponential shape Ira Fulton School of Engineering