Intro to Recursion Fibonacci Numbers 1 f 0

Intro to Recursion

Fibonacci Numbers (1) • • f 0 = 1 f 1 = 1 f 2 = 1 + 1 = 2 f 3 = 2 + 1 = 3 f 4 = 3 + 2 = 5 f 5 = 5 + 3 = 8 f 6 = 8 + 5 = 13 • In general: fn = fn-1 + fn-2 • for n ≥ 2 f 0 = 1 f 1 = 1

Fibonacci Numbers (2) The Fibonacci number problem has the recursive property The problem fibonacci(n) (= fn) can be solved using the solution of two smaller problem: The base (simple) cases n = 0 and n = 1 of the Fibonacci problem can be solved readily:

Fibonacci Numbers (3) 1. Which smaller problem do we use to solve fibonacci(n):

Fibonacci Numbers (4) 2. How do we use the solution sol 1 to solve fibonacci(n) 3. Because we used fibonacci(n− 2), we will need the solution for 2 base cases:

Fibonacci Numbers (5)

The recursive binary search algorithm(1) • You are given a sorted array (of numbers) • Locate the array element that has the value x

The recursive binary search algorithm(2) • Locate the array element that has the value 27

The recursive binary search algorithm(3) • Locate the array element that has the value 28

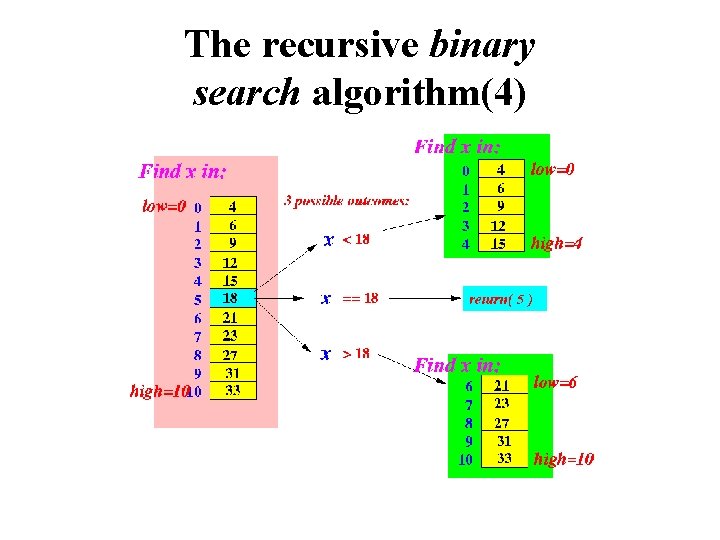
The recursive binary search algorithm(4)

The recursive binary search algorithm(5)