Intro to Exponents Learn to evaluate expressions with

Focus 11 - Learning Goal: The student will be able to work with integer

Review Find the product. 1. 5 • 5 • 5 625 2. 3 •

The term 27 is called a power. If a number is in exponential form,

Write in exponential form. A. 4 • 4 • 4 • 4 = 44

Write in exponential form. C. (– 6) • (– 6) = (– 6)3 Identify

Write in exponential form. A. x • x • x= x 5 Identify how

Evaluate. Find the product of five 3’s. A. 35 35 = 3 • 3

Evaluate. Find the product of four 7’s. C. 74 74 = 7 • 7

Simplifying Expressions Containing Powers Simplify (25 – 32 ) + 6(4) = (32 –

Simplify (32 – 82) + 2 • 3 = (9 – 64) + 2

Slides: 11

Download presentation

Intro to Exponents Learn to evaluate expressions with exponents.

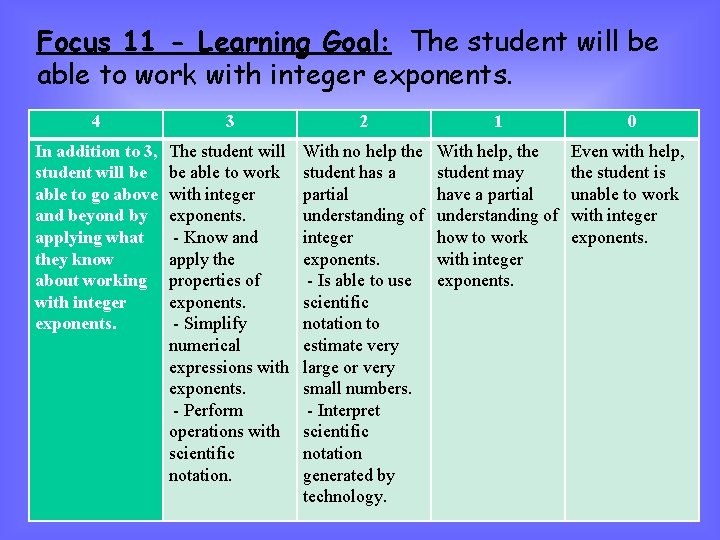
Focus 11 - Learning Goal: The student will be able to work with integer exponents. 4 3 2 1 0 In addition to 3, student will be able to go above and beyond by applying what they know about working with integer exponents. The student will be able to work with integer exponents. - Know and apply the properties of exponents. - Simplify numerical expressions with exponents. - Perform operations with scientific notation. With no help the student has a partial understanding of integer exponents. - Is able to use scientific notation to estimate very large or very small numbers. - Interpret scientific notation generated by technology. With help, the student may have a partial understanding of how to work with integer exponents. Even with help, the student is unable to work with integer exponents.

Review Find the product. 1. 5 • 5 • 5 625 2. 3 • 3 27 3. (– 7) • (– 7) – 343 4. 9 • 9 81

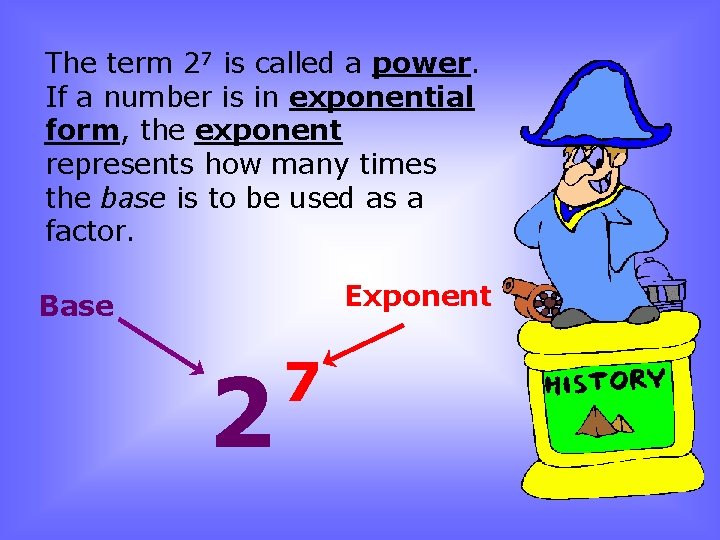
The term 27 is called a power. If a number is in exponential form, the exponent represents how many times the base is to be used as a factor. Exponent Base 2 7

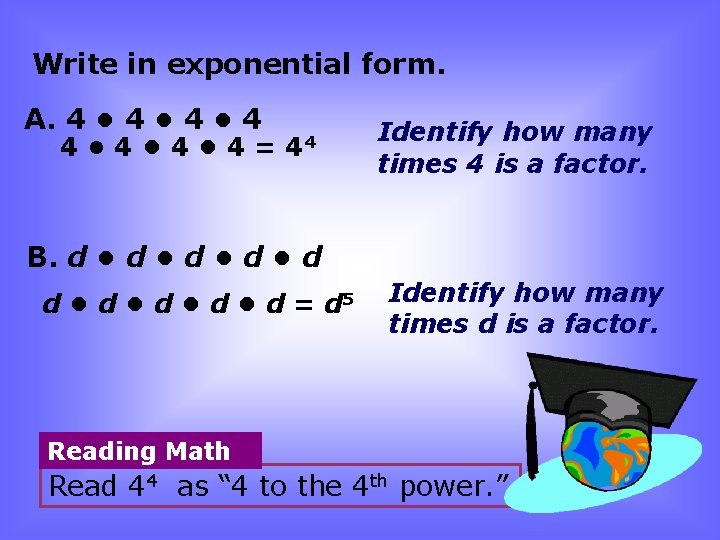
Write in exponential form. A. 4 • 4 • 4 • 4 = 44 Identify how many times 4 is a factor. B. d • d • d = d 5 Identify how many times d is a factor. Reading Math Read 44 as “ 4 to the 4 th power. ”

Write in exponential form. C. (– 6) • (– 6) = (– 6)3 Identify how many times – 6 is a factor. Remember to keep the – sign inside the ( )! If it is outside, your answer will be negative even if you have an even number of – signs. D. 5 • 5 = 52 Identify how many times 5 is a factor.

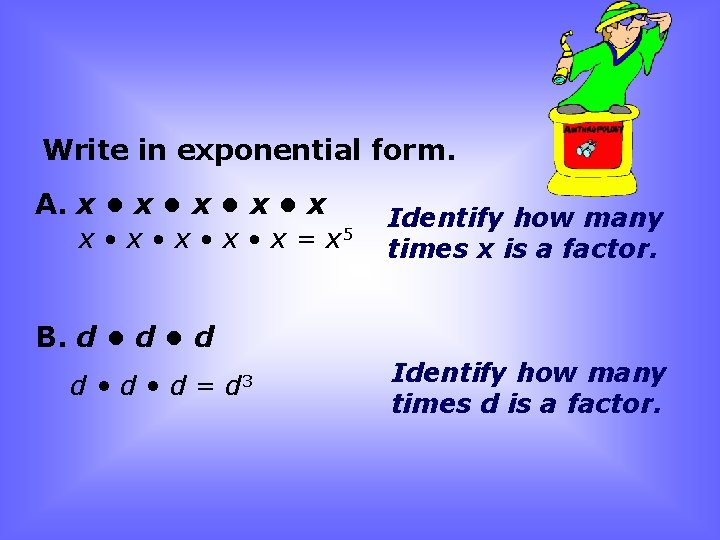
Write in exponential form. A. x • x • x= x 5 Identify how many times x is a factor. B. d • d • d = d 3 Identify how many times d is a factor.

Evaluate. Find the product of five 3’s. A. 35 35 = 3 • 3 • 3 = 243 B. (– 3)5 Find the product of five – 3’s. (– 3)5 = (– 3) • (– 3) = – 243 Helpful Hint Always use parentheses to raise a negative number to a power.

Evaluate. Find the product of four 7’s. C. 74 74 = 7 • 7 • 7 = 2401 D. (– 9)3 Find the product of three – 9’s. (– 9)3 = (– 9) • (– 9) = – 729

Simplifying Expressions Containing Powers Simplify (25 – 32 ) + 6(4) = (32 – 9) + 6(4) Evaluate the exponents. = (23) + 6(4) Subtract inside the parentheses. = 23 + 24 Multiply from left to right. = 47 Add from left to right.

Simplify (32 – 82) + 2 • 3 = (9 – 64) + 2 • 3 = (– 55) + 2 • 3 = – 55 + 6 = – 49 Evaluate the exponents. Subtract inside the parentheses. Multiply from left to right. Add from left to right.