INTRO LOGIC DAY 10 Derivations in SL 2

INTRO LOGIC DAY 10 Derivations in SL 2 1

Review We demonstrate (show) that an argument is valid by deriving (deducing) its conclusion from its premises using a few fundamental modes of reasoning. 2

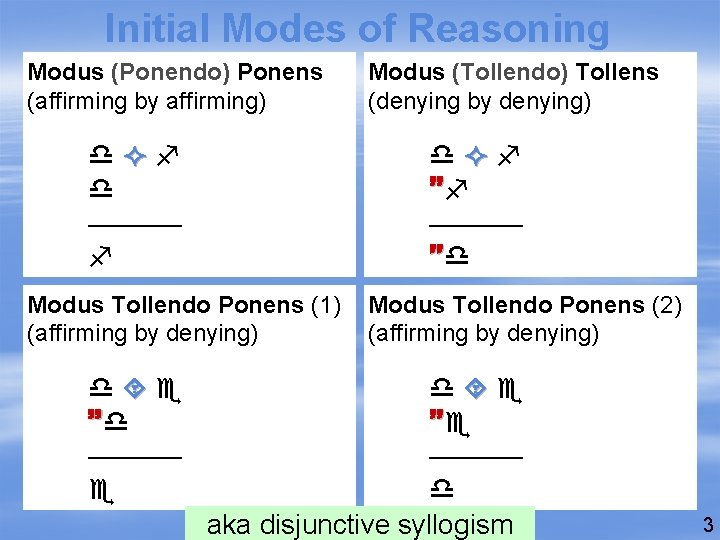
Initial Modes of Reasoning Modus (Ponendo) Ponens (affirming by affirming) –––––– Modus Tollendo Ponens (1) (affirming by denying) –––––– Modus (Tollendo) Tollens (denying by denying) Modus Tollendo Ponens (2) (affirming by denying) –––––– aka disjunctive syllogism 3

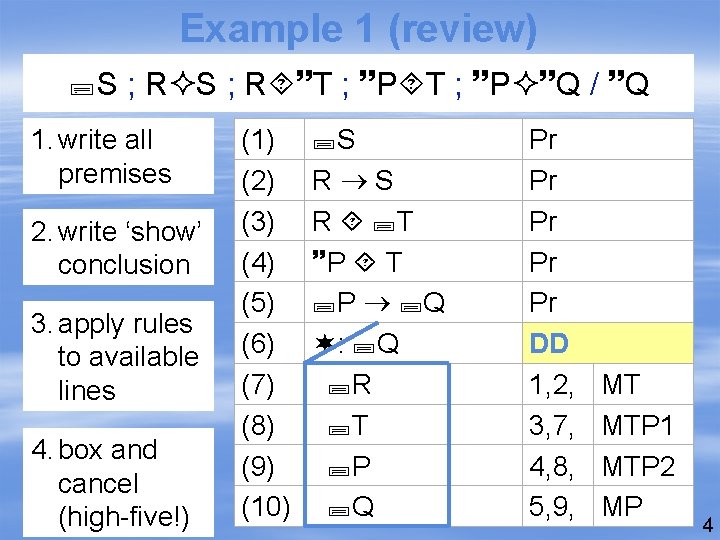
Example 1 (review) S ; R T ; P Q / Q 1. write all premises 2. write ‘show’ conclusion 3. apply rules to available lines 4. box and cancel (high-five!) (1) (2) (3) (4) (5) (6) (7) (8) (9) (10) S R T P Q : Q R T P Q Pr Pr Pr DD 1, 2, 3, 7, 4, 8, 5, 9, MT MTP 1 MTP 2 MP 4

other high-fives Tek gives Manny a high-five Tek gives A-Rod a high-five 5

Rule Sheet provided on exams available on course web page (textbook) keep this in front of you when doing homework don’t make up your own rules 6

Rules discussed Today 7

Rules of Inference – Basic Idea Every connective has (1) a take-out rule also called an: elimination-rule OUT-rule (2) a put-in rule also called an: introduction-rule IN-rule 8

Ampersand-Out (&O) if you have a conjunction & then you are entitled to infer –––––– its first conjunct if you have a conjunction then you are entitled to infer its second conjunct & –––––– ‘have’ means ‘have as a whole line’ rules apply only to whole lines not pieces of lines 9

Ampersand-IN (&I) if you have a formula and you have a formula then you are entitled to infer –––––– their (first) conjunction & if you have a formula and you have a formula then you are entitled to infer their (second) conjunction –––––– & 10

Wedge-Out ( O) if you have a disjunction and you have the negation of its 1 st disjunct then you are entitled to infer –––––– its second disjunct if you have a disjunction and you have the negation of its 2 nd disjunct then you are entitled to infer its first disjunct –––––– what we earlier called ‘modus tollendo ponens’ 11

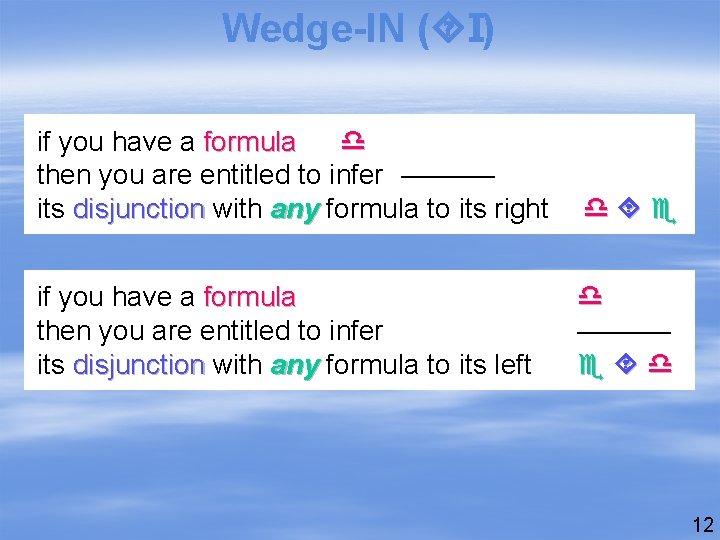
Wedge-IN ( I) if you have a formula then you are entitled to infer –––––– its disjunction with any formula to its right if you have a formula then you are entitled to infer its disjunction with any formula to its left –––––– 12

Arrow-Out ( O) if you have a conditional and you have its antecedent then you are entitled to infer its consequent –––––– if you have a conditional and you have the negation of its consequent then you are entitled to infer the negation of its antecedent –––––– What we earlier called ‘modus ponens’ and ‘modus tollens’ 13

Arrow-Introduction THERE IS NO SUCH THING AS ARROW-IN ( I) what we have instead is CONDITIONAL DERIVATION (CD) which we examine later 14

Double-Negation (DN) if you have a formula then you are entitled to infer its double-negative ––––– if you have a double-negative then you are entitled to infer ––––– the formula rules apply only to whole lines not pieces of lines 15

Direct Derivation The Original and Fundamental -Rule : ° ° ° DD In Direct Derivation (DD), one directly arrives at the very formula one is trying to show. 16

Example 2 S ; R S ; R T ; P T ; P Q / Q (1) (2) (3) (4) (5) (6) (7) (8) (9) (10) S R T P Q : Q R T P Q Pr Pr Pr DD 1, 2, 3, 7, 4, 8, 5, 9, O O 17

Arrow-Out Strategy If you have a line of the form , then try to apply arrow-out ( O), which requires a second formula as input, in particular, either or . have find or deduce 18

Example 3 S ; R T ; P Q / Q (1) (2) (3) (4) (5) (6) (7) (8) (9) (10) S R T P Q : Q R T P Q Pr Pr Pr DD 1, 2, 3, 7, 4, 8, 5, 9, O O 19

Wedge-Out Strategy If you have a line of the form , then try to apply wedge-out ( O), which requires a second formula as input, in particular, either or . have find or deduce 20

Example 4 (P Q) R ; [(P Q) R] R ; (P Q) (Q R) / Q (1) (2) (3) (4) (5) (6) (7) (8) (P Q) R [(P Q) R] R (P Q) (Q R) : Q R P Q Q R R Pr Pr Pr DD 1, 2, 1, 5, 3, 6, 5, 7, O O 21

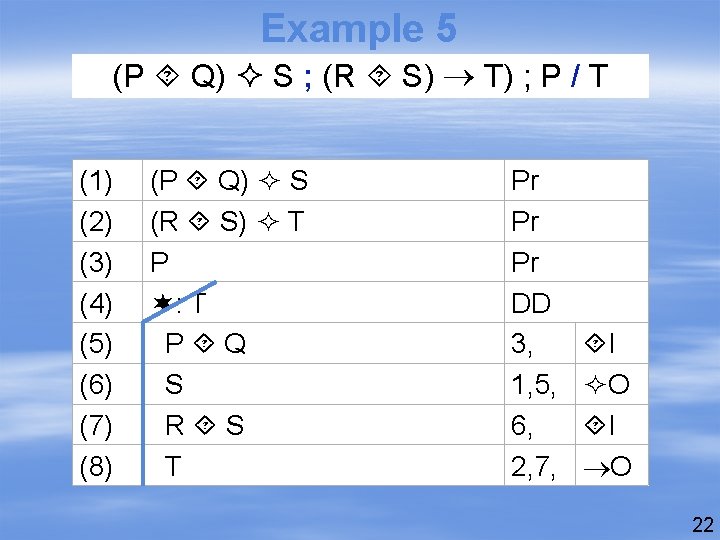
Example 5 (P Q) S ; (R S) T) ; P / T (1) (2) (3) (4) (5) (6) (7) (8) (P Q) S (R S) T P : T P Q S R S T Pr Pr Pr DD 3, 1, 5, 6, 2, 7, I O 22

Wedge-In Strategy If you need then look for either disjunct: find OR find then apply v. I to get 23

Example 6 P Q ; R (Q S) ; R T ; T & P / Q & S (1) (2) (3) (4) (5) (6) (7) (8) (9) (10) (11) (12) P Q R (Q S) R T T & P Q & S T P Q R Q S S Q&S Pr Pr DD 4, &O 1, 7, 3, 6, 2, 9, 8, 10, 8, 11, O O &I 24

Ampersand-Out Strategy If you have a line of the form & , then apply ampersand-out (&O), which can be applied immediately to produce and 25

Ampersand-In Strategy If you are trying to find or show & then look for both conjuncts: find AND find then apply &I to get & 26

THE END 27