Intrinsic dimension of data representations in deep neural

Intrinsic dimension of data representations in deep neural networks Alessandro Laio

Intrinsic dimension of data representations in deep neural networks machine learning Jakob Macke (TUM) Alessio Ansuini (SISSA) neuroscience Davide Zoccolan physics Alessandro Laio (SISSA)

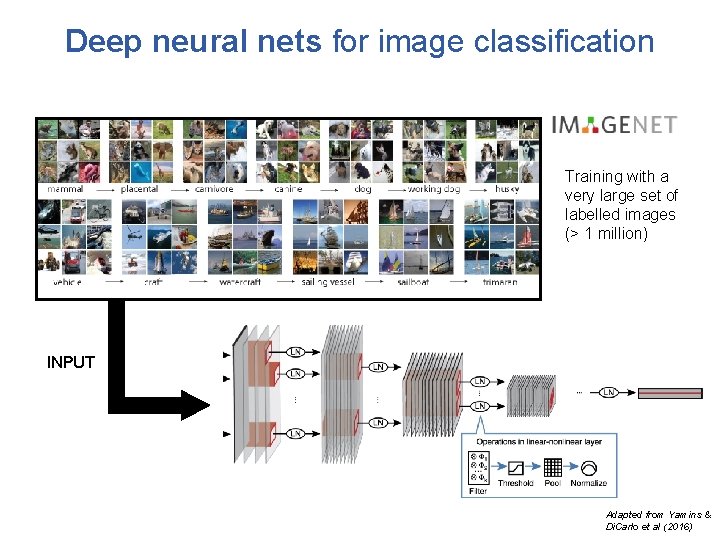
Deep neural nets for image classification Training with a very large set of labelled images (> 1 million) INPUT Adapted from Yamins & Di. Carlo et al (2016)

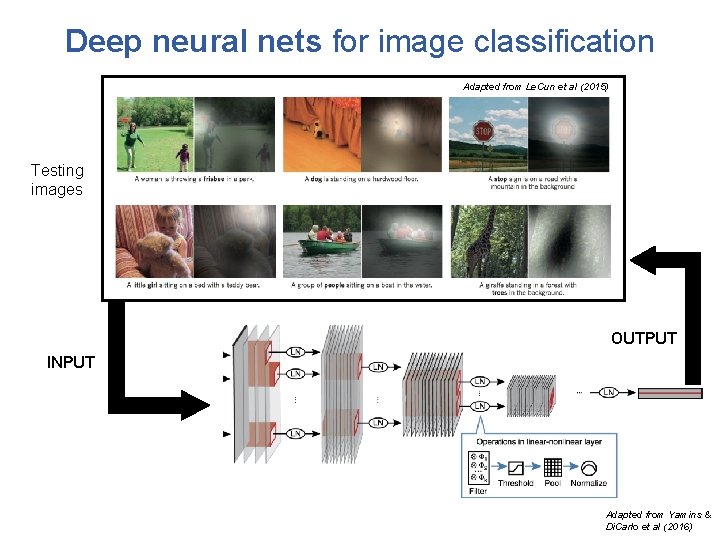
Deep neural nets for image classification Adapted from Le. Cun et al (2015) Testing images OUTPUT INPUT Adapted from Yamins & Di. Carlo et al (2016)

Deep neural nets for image classification Adapted from Le. Cun et al (2015) Testing images

Machine vs. human vision Artificial vision Human vision What do these processes have in common?

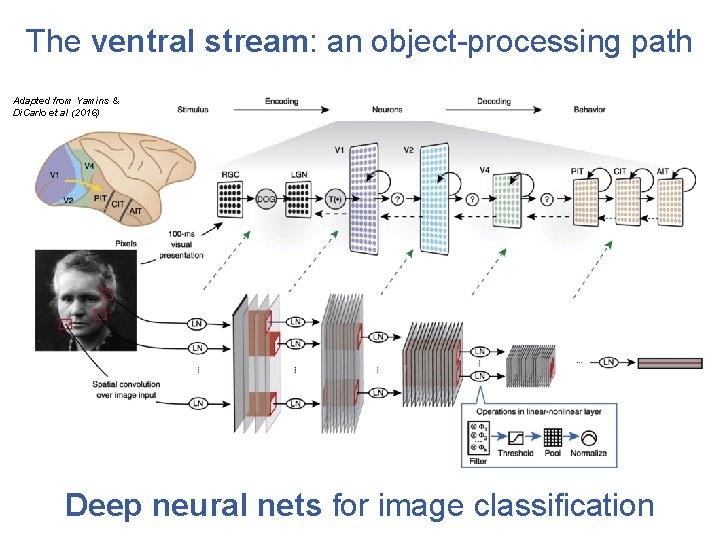
The ventral stream: an object-processing path Adapted from Yamins & Di. Carlo et al (2016) Deep neural nets for image classification

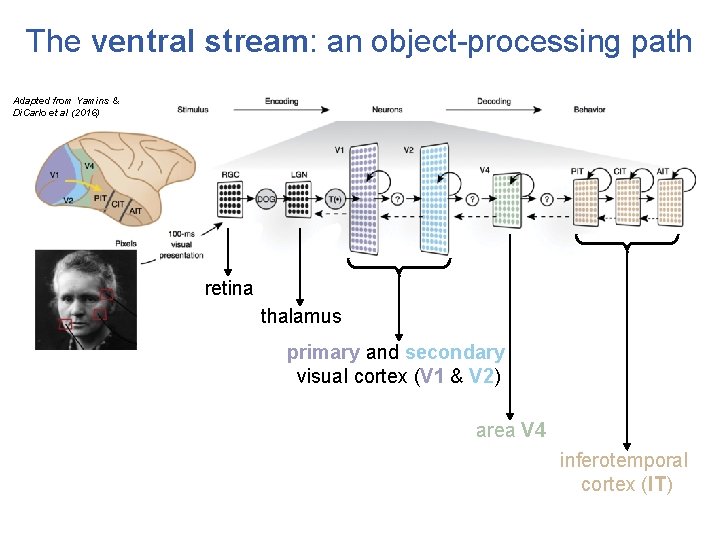
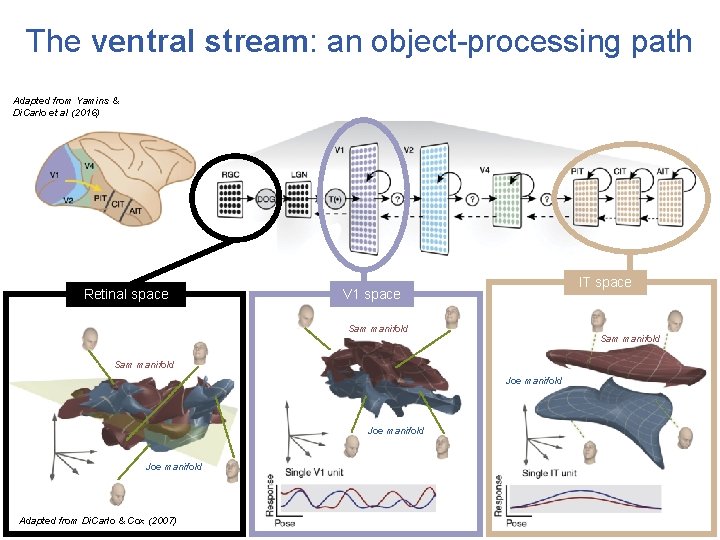
The ventral stream: an object-processing path Adapted from Yamins & Di. Carlo et al (2016) retina thalamus primary and secondary visual cortex (V 1 & V 2) area V 4 inferotemporal cortex (IT)

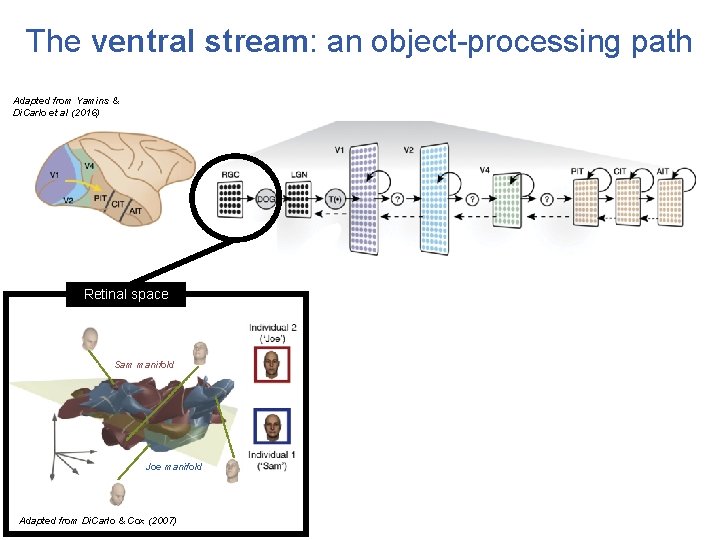
The ventral stream: an object-processing path Adapted from Yamins & Di. Carlo et al (2016) Retinal space Sam manifold Joe manifold Adapted from Di. Carlo & Cox (2007)

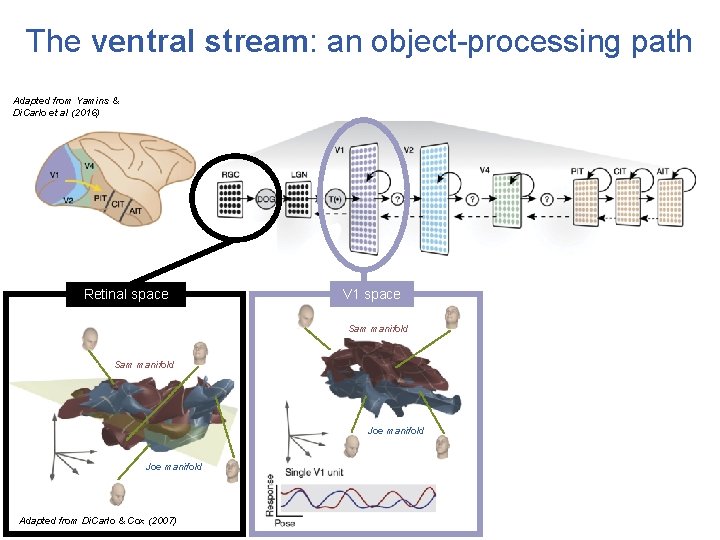
The ventral stream: an object-processing path Adapted from Yamins & Di. Carlo et al (2016) Retinal space V 1 space Sam manifold Joe manifold Adapted from Di. Carlo & Cox (2007)

The ventral stream: an object-processing path Adapted from Yamins & Di. Carlo et al (2016) Retinal space IT space V 1 space Sam manifold Joe manifold Adapted from Di. Carlo & Cox (2007)

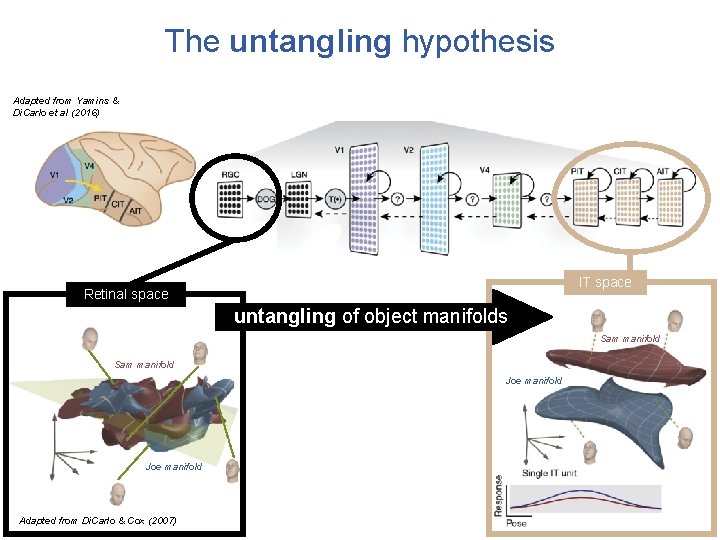
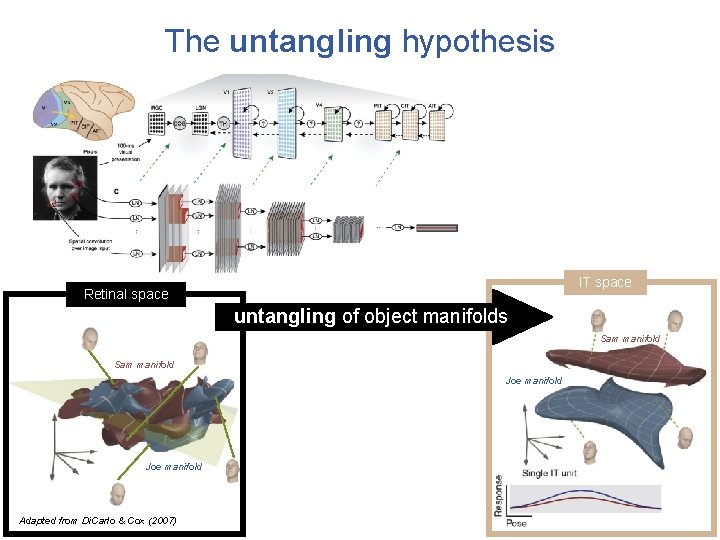
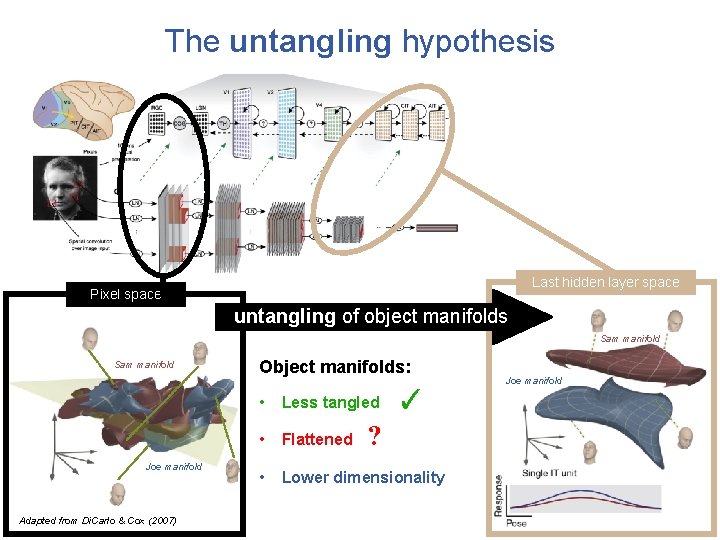
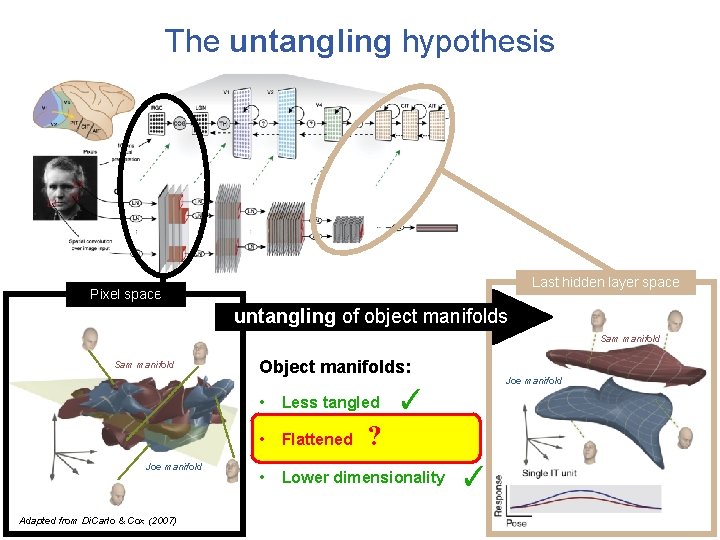
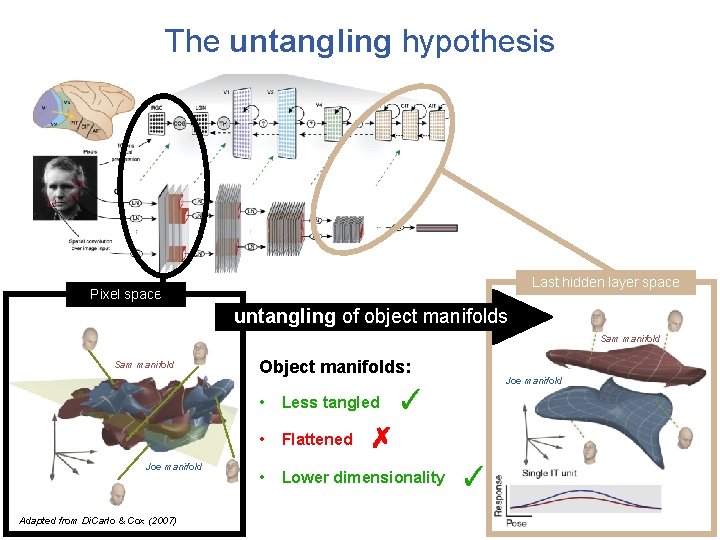
The untangling hypothesis Adapted from Yamins & Di. Carlo et al (2016) IT space Retinal space untangling of object manifolds Sam manifold Joe manifold Adapted from Di. Carlo & Cox (2007)

The untangling hypothesis IT space Retinal space untangling of object manifolds Sam manifold Joe manifold Adapted from Di. Carlo & Cox (2007)

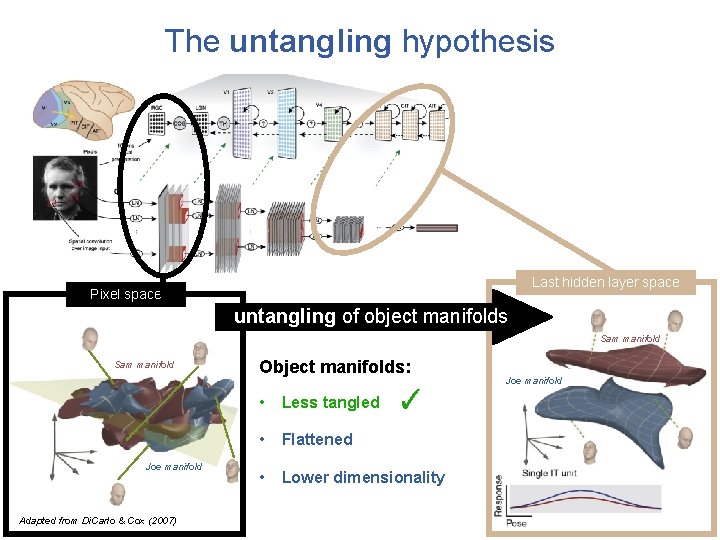
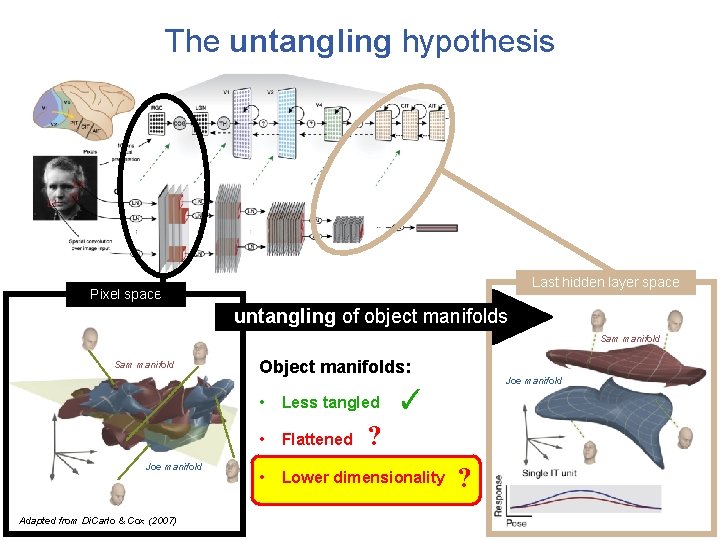
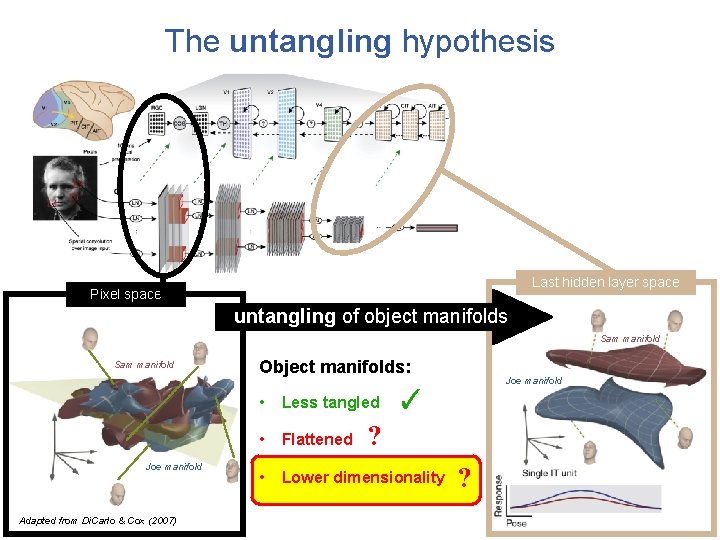
The untangling hypothesis Last hidden layer space Pixel space untangling of object manifolds Sam manifold Joe manifold Adapted from Di. Carlo & Cox (2007) Object manifolds: ✓ • Less tangled • Flattened • Lower dimensionality Joe manifold

The untangling hypothesis Last hidden layer space Pixel space untangling of object manifolds Sam manifold Joe manifold Adapted from Di. Carlo & Cox (2007) Object manifolds: ✓ • Less tangled • Flattened • Lower dimensionality ? Joe manifold

The untangling hypothesis Last hidden layer space Pixel space untangling of object manifolds Sam manifold Joe manifold Adapted from Di. Carlo & Cox (2007) Object manifolds: Joe manifold ✓ • Less tangled • Flattened • Lower dimensionality ? ?

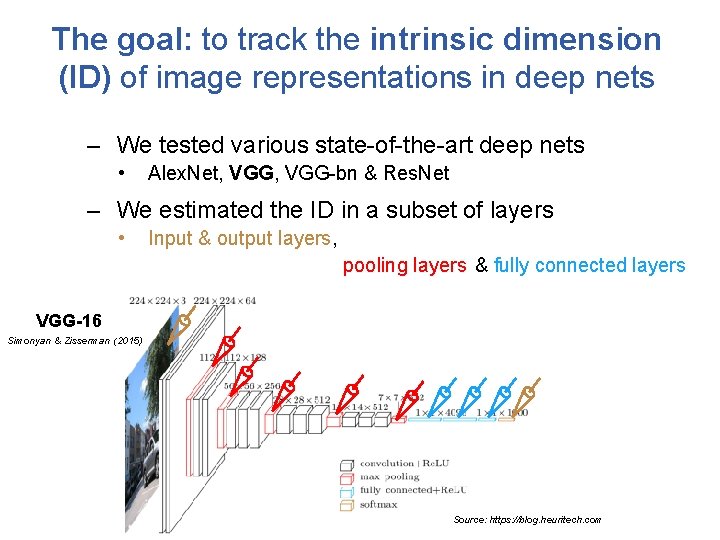
The goal: to track the intrinsic dimension (ID) of image representations in deep nets – We tested various state-of-the-art deep nets • Alex. Net, VGG-bn & Res. Net – We estimated the ID in a subset of layers • Input & output layers, pooling layers & fully connected layers VGG-16 Simonyan & Zisserman (2015) Source: https: //blog. heuritech. com

The goal: to track the intrinsic dimension (ID) of image representations in deep nets – We tested various state-of-the-art deep nets • Alex. Net, VGG-bn & Res. Net – We estimated the ID in a subset of layers • Input & output layers, pooling layers & fully connected layers 1. Empirical questions – How does the ID vary across the layers of a deep net? – How linear (i. e. , flat) are the data manifolds? – Is there any relationship between ID in the last hidden layer and classification performance of the network?

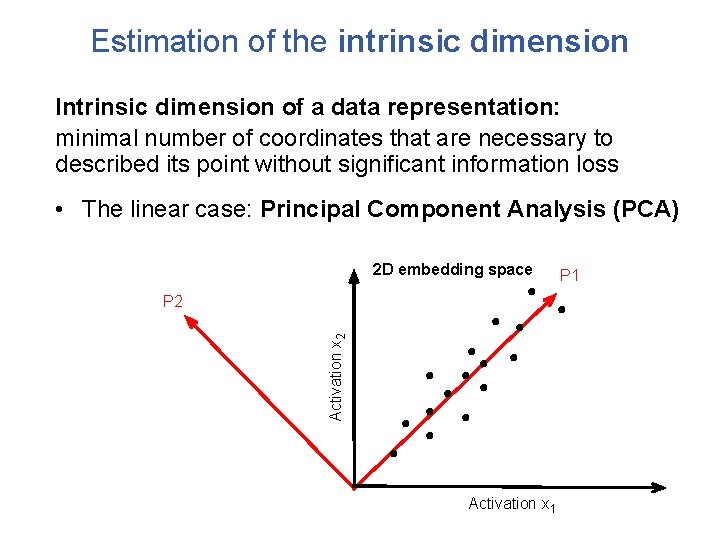
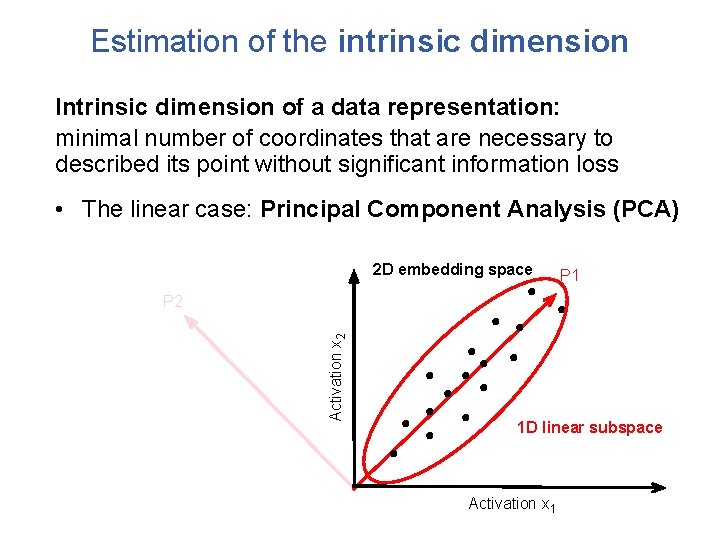
Estimation of the intrinsic dimension Intrinsic dimension of a data representation: minimal number of coordinates that are necessary to described its point without significant information loss • The linear case: Principal Component Analysis (PCA) 2 D embedding space Activation x 2 P 2 Activation x 1 P 1

Estimation of the intrinsic dimension Intrinsic dimension of a data representation: minimal number of coordinates that are necessary to described its point without significant information loss • The linear case: Principal Component Analysis (PCA) 2 D embedding space P 1 Activation x 2 P 2 1 D linear subspace Activation x 1

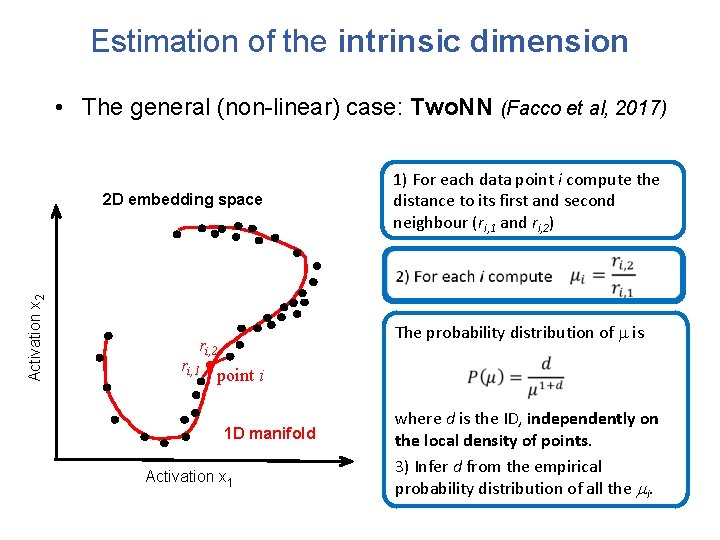
Estimation of the intrinsic dimension • The general (non-linear) case: Two. NN (Facco et al, 2017) Activation x 2 2 D embedding space The probability distribution of m is ri, 2 ri, 1 1) For each data point i compute the distance to its first and second neighbour (ri, 1 and ri, 2) point i 1 D manifold Activation x 1 where d is the ID, independently on the local density of points. 3) Infer d from the empirical probability distribution of all the mi.

Results 1 Evolution of ID across the layers of a deep net pre-trained on Image. Net VGG-16 Simonyan & Zisserman (2015) Source: https: //blog. heuritech. com

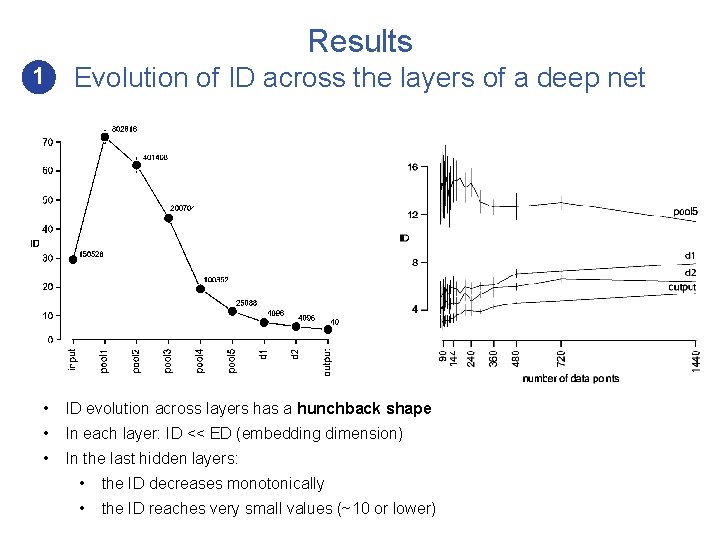
Results 1 Evolution of ID across the layers of a deep net • ID evolution across layers has a hunchback shape • In each layer: ID << ED (embedding dimension) • In the last hidden layers: • the ID decreases monotonically • the ID reaches very small values (~10 or lower)

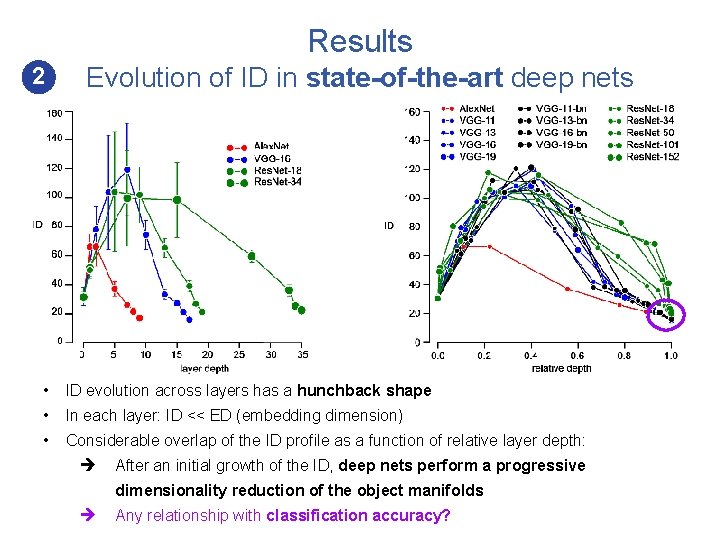
Results 2 Evolution of ID in state-of-the-art deep nets • Four families of state-of-the art deep net architectures: 1. 2. 3. 4. Alex. Net VGG-bn Res. Net • Pre-trained on Image. Net • ID computed for the 7 most populated categories (500 images each)

Results 2 Evolution of ID in state-of-the-art deep nets • ID evolution across layers has a hunchback shape • In each layer: ID << ED (embedding dimension) • Considerable overlap of the ID profile as a function of relative layer depth: After an initial growth of the ID, deep nets perform a progressive dimensionality reduction of the object manifolds Any relationship with classification accuracy?

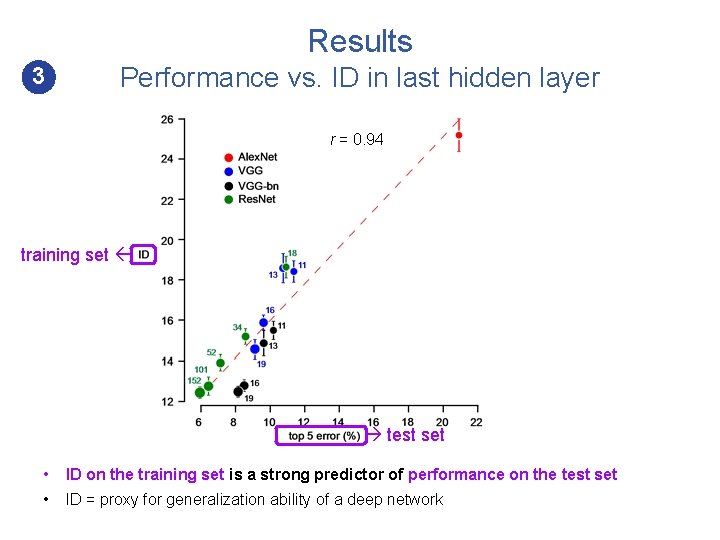
Results Performance vs. ID in last hidden layer 3 • Four families of state-of-the art deep net architectures: 1. 2. 3. 4. Alex. Net VGG-bn Res. Net • Pre-trained on Image. Net • ID computed over a a random mixture of 2000 training images • Classification accuracy = top 5 -score error

Results 3 Performance vs. ID in last hidden layer r = 0. 94 training set r = 0. 99 test set • ID on the training set is a strong predictor of performance on the test set • ID = proxy for generalization ability of a deep network

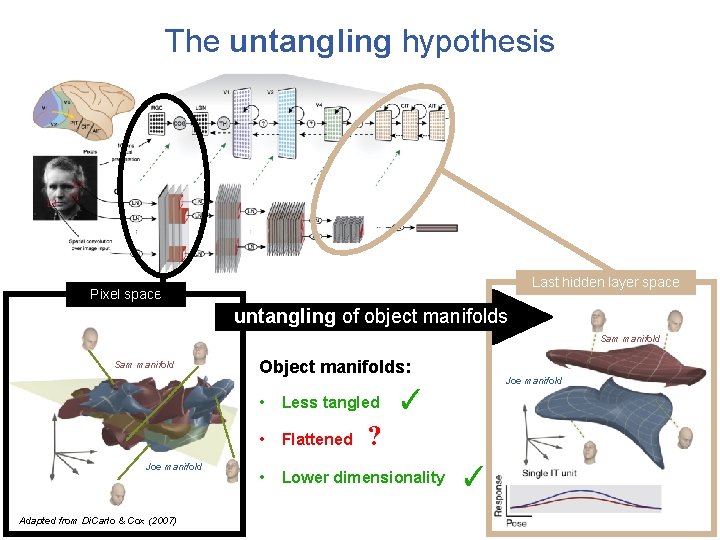
The untangling hypothesis Last hidden layer space Pixel space untangling of object manifolds Sam manifold Joe manifold Adapted from Di. Carlo & Cox (2007) Object manifolds: Joe manifold ✓ • Less tangled • Flattened • Lower dimensionality ? ?

The untangling hypothesis Last hidden layer space Pixel space untangling of object manifolds Sam manifold Joe manifold Adapted from Di. Carlo & Cox (2007) Object manifolds: Joe manifold ✓ • Less tangled • Flattened • Lower dimensionality ? ✓

The untangling hypothesis Last hidden layer space Pixel space untangling of object manifolds Sam manifold Joe manifold Adapted from Di. Carlo & Cox (2007) Object manifolds: Joe manifold ✓ • Less tangled • Flattened • Lower dimensionality ? ✓

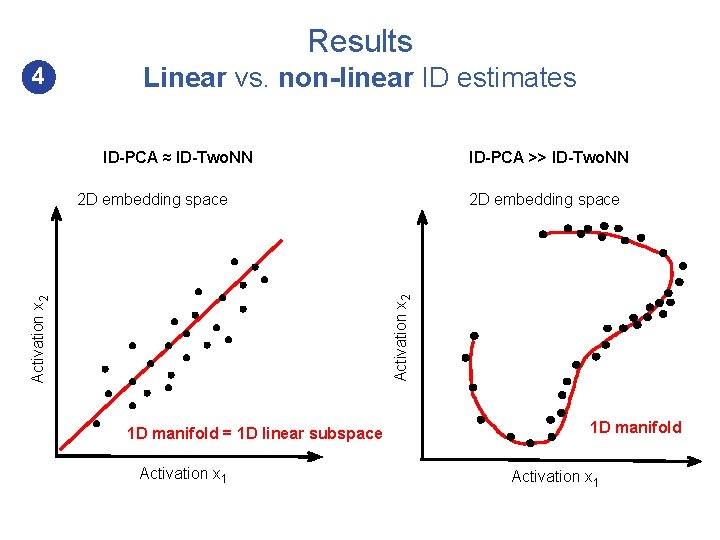
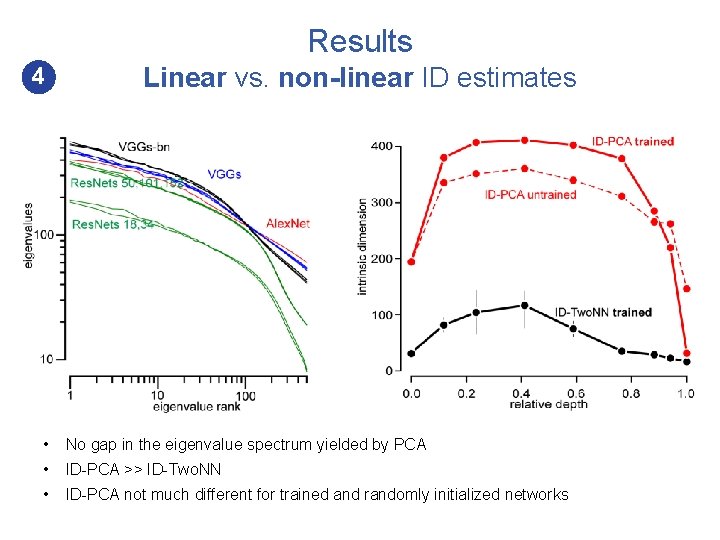
Results 4 Linear vs. non-linear ID estimates ID-PCA ≈ ID-Two. NN ID-PCA >> ID-Two. NN 2 D embedding space Activation x 2 2 D embedding space 1 D manifold = 1 D linear subspace Activation x 1 1 D manifold Activation x 1

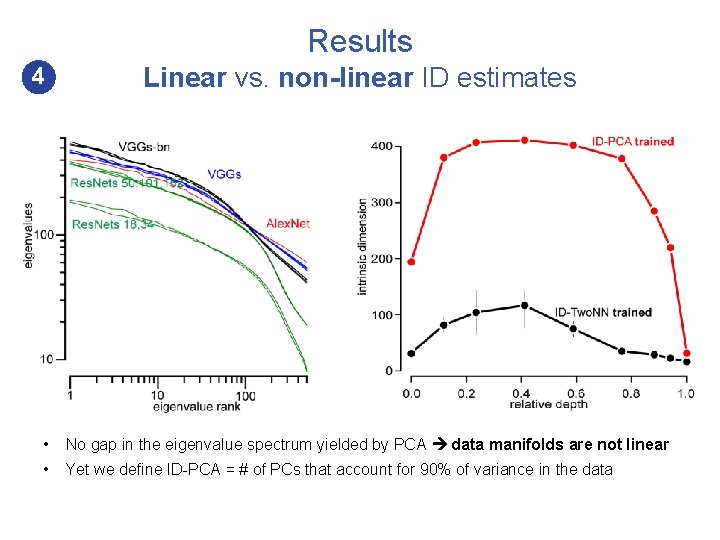
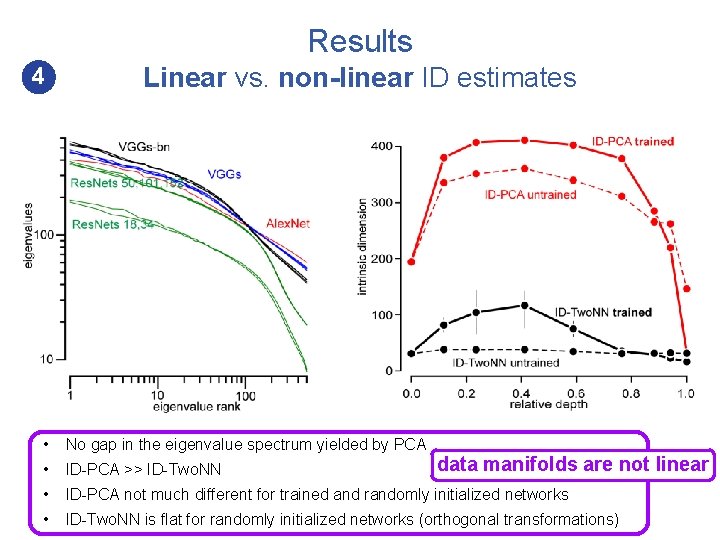
Results 4 Linear vs. non-linear ID estimates • No gap in the eigenvalue spectrum yielded by PCA data manifolds are not linear • Yet we define ID-PCA = # of PCs that account for 90% of variance in the data

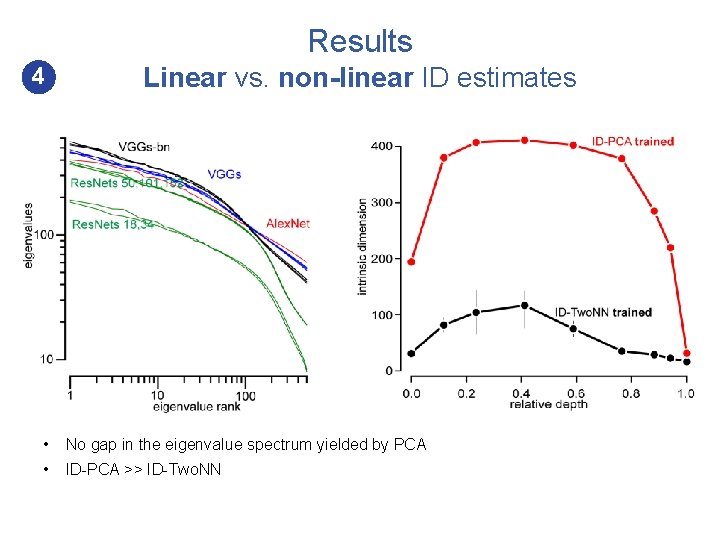
Results 4 Linear vs. non-linear ID estimates • No gap in the eigenvalue spectrum yielded by PCA • ID-PCA >> ID-Two. NN

Results 4 Linear vs. non-linear ID estimates • No gap in the eigenvalue spectrum yielded by PCA • ID-PCA >> ID-Two. NN • ID-PCA not much different for trained and randomly initialized networks

Results 4 Linear vs. non-linear ID estimates • No gap in the eigenvalue spectrum yielded by PCA • ID-PCA >> ID-Two. NN • ID-PCA not much different for trained and randomly initialized networks • ID-Two. NN is flat for randomly initialized networks (orthogonal transformations) data manifolds are not linear

The untangling hypothesis Last hidden layer space Pixel space untangling of object manifolds Sam manifold Joe manifold Adapted from Di. Carlo & Cox (2007) Object manifolds: Joe manifold ✓ • Less tangled • Flattened • Lower dimensionality ✗ ✓

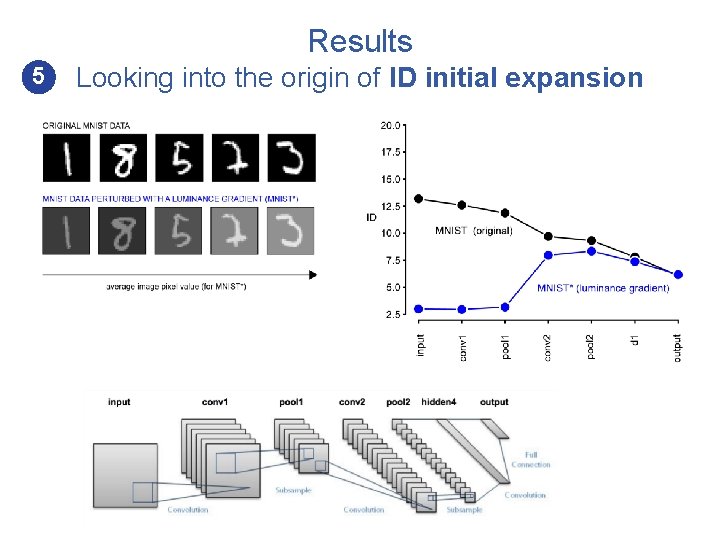
Results 5 Looking into the origin of ID initial expansion VGG-16 Source: https: //blog. heuritech. com

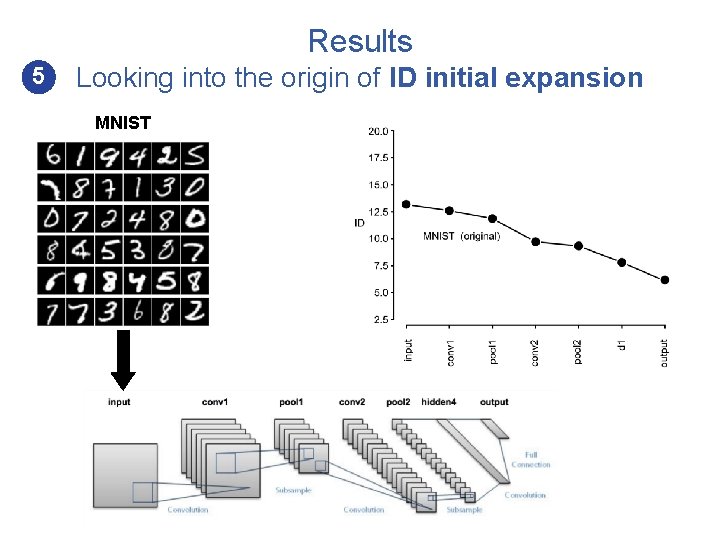
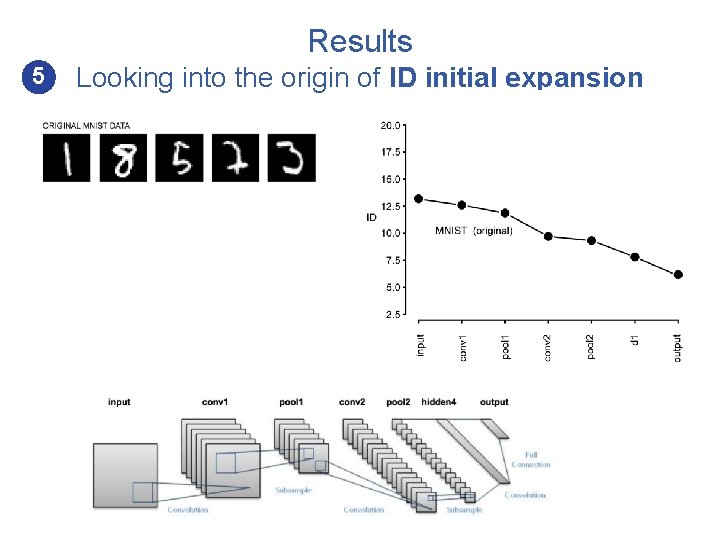
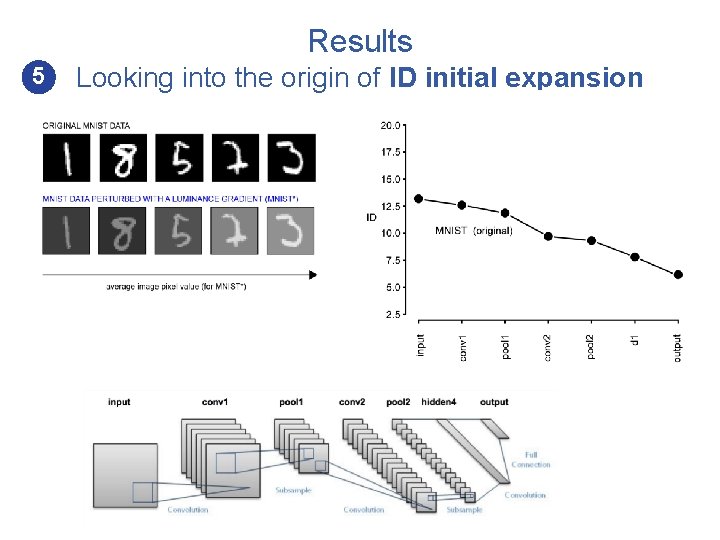
Results 5 Looking into the origin of ID initial expansion MNIST

Results 5 Looking into the origin of ID initial expansion MNIST

Results 5 Looking into the origin of ID initial expansion

Results 5 Looking into the origin of ID initial expansion

Results 5 Looking into the origin of ID initial expansion

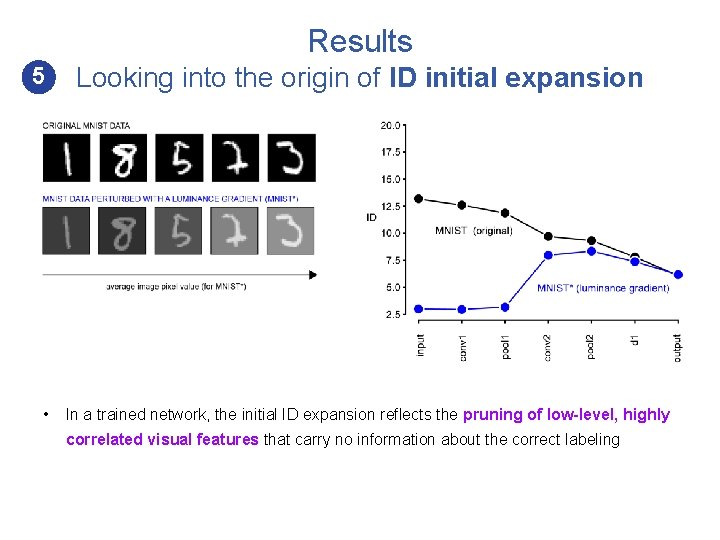
Results 5 • Looking into the origin of ID initial expansion In a trained network, the initial ID expansion reflects the pruning of low-level, highly correlated visual features that carry no information about the correct labeling

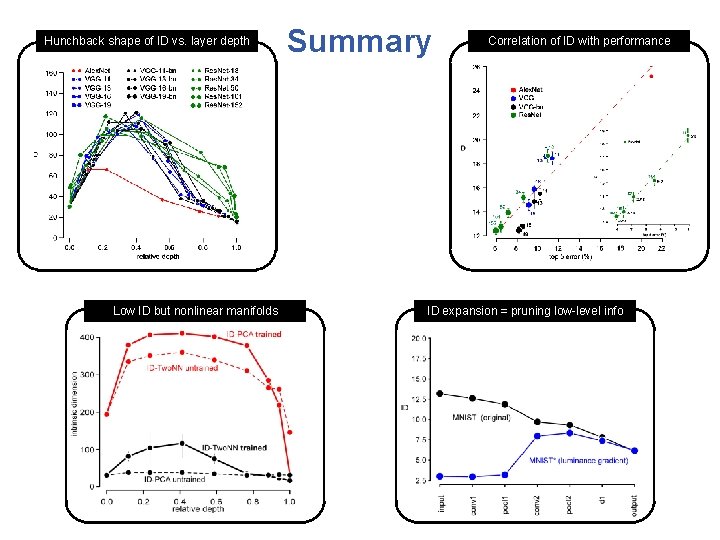
Hunchback shape of ID vs. layer depth Low ID but nonlinear manifolds Summary Correlation of ID with performance ID expansion = pruning low-level info

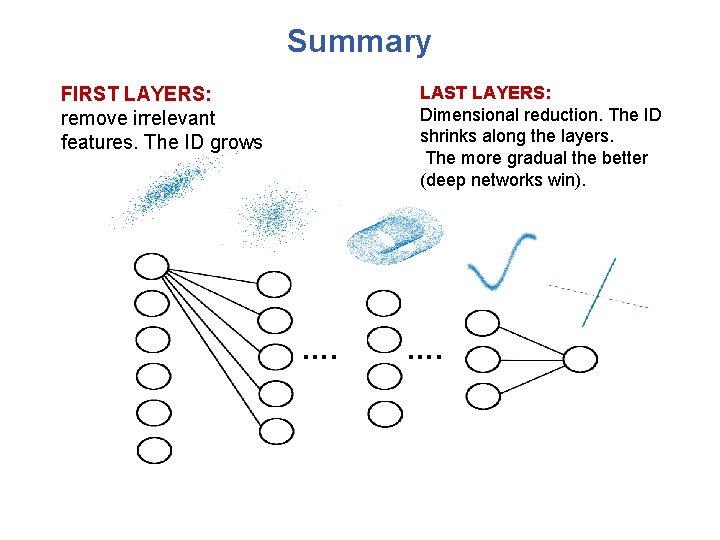
Summary LAST LAYERS: Dimensional reduction. The ID shrinks along the layers. The more gradual the better (deep networks win). FIRST LAYERS: remove irrelevant features. The ID grows ….

Acknowledgments Davide Zoccolan (SISSA) Alessio Ansuini (SISSA) Jakob Macke (TUM) 2019 Vancouver