INTRACLASS CORRELATION COEFFICIENT ICC Pearsons correlation measures the









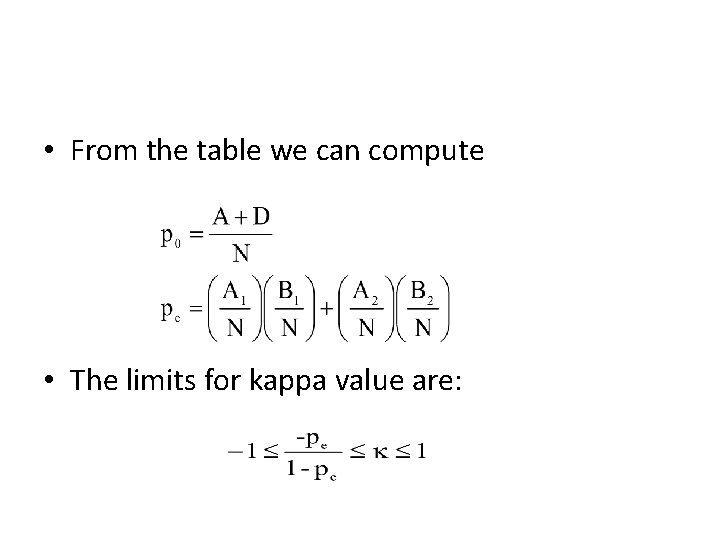

- Slides: 13

INTRACLASS CORRELATION COEFFICIENT ( ICC )

• Pearson’s correlation measures the degree of linear relationship between two variables • This can be called ‘ inter class correlation ‘ • We study associations/ relationships within classes: – Anxiety in families measured by observing twins – Scoring of paintings by two or more judges – Measuring the same quantity using two different instruments

• The variables measured/scored are the same by the raters/judges • In these cases we use intraclass correlation to measure agreement or inter-rater agreement • All situations in which an intraclass correlation is desirable involve measures on different entities/subjects • The entities measured constitute a random factor

• Based on the various assumptions on random factors different models of ICC are developed • One-way random effect model • Two measurements are considered. Each subject is rated by different group of raters. Analysis is carried out using one way ANOVA. • Two way random effect model • There are different raters and the order of the measures is important. Multiple measures on the same subject may be considered. Each rater scores a different group of subjects.

• Random factorial design: In this design each subject is scored by the same group of raters. For the simple case the ICC is computed by the following formula

KAPPA STATISTICS • Different approaches may be used to diagnose a disease • Two experts may examine a petient and give their opinion • Two different measuring devices may be used and we want to know agreement between the measurements • In all these cases we are interested in measuring agreements

• Kappa statistics ( Cohen’s kappa statistics ) is one such measure used to compare different methods • Kappa statistics ( ) is interpreted as the proportion of agreement among raters / methods after chance agreement has been removed

• The formula for kappa statistics is given by: • Where

• Expected agreement is estimated by the proportion of agreements that would be expected if the observed ratings are completely random • Use of kappa statistics requires the following assumptions – Subjects are independent – Raters score indepenently – Rating categories are mutually exclusive

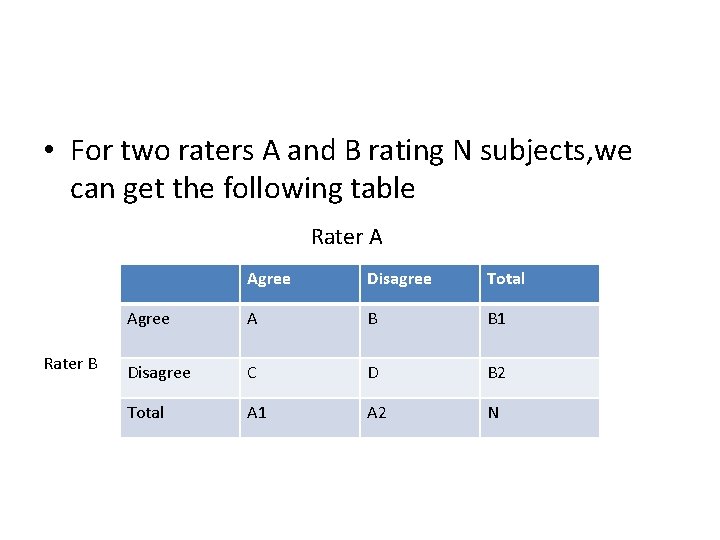
• For two raters A and B rating N subjects, we can get the following table Rater A Rater B Agree Disagree Total Agree A B B 1 Disagree C D B 2 Total A 1 A 2 N
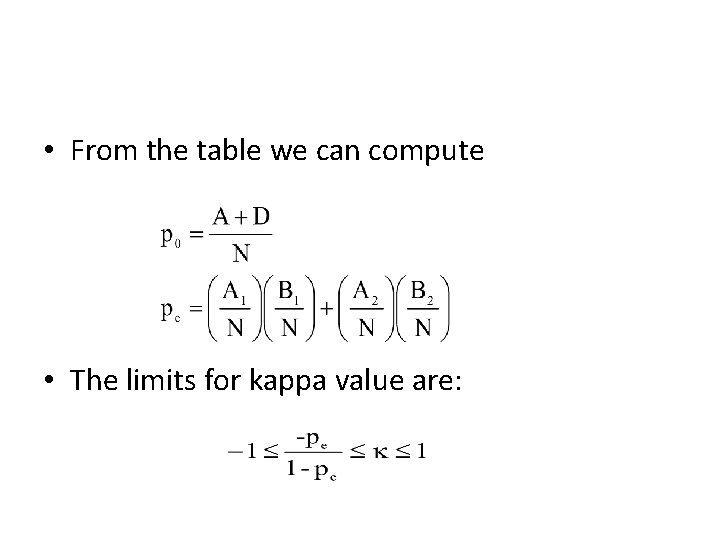
• From the table we can compute • The limits for kappa value are:

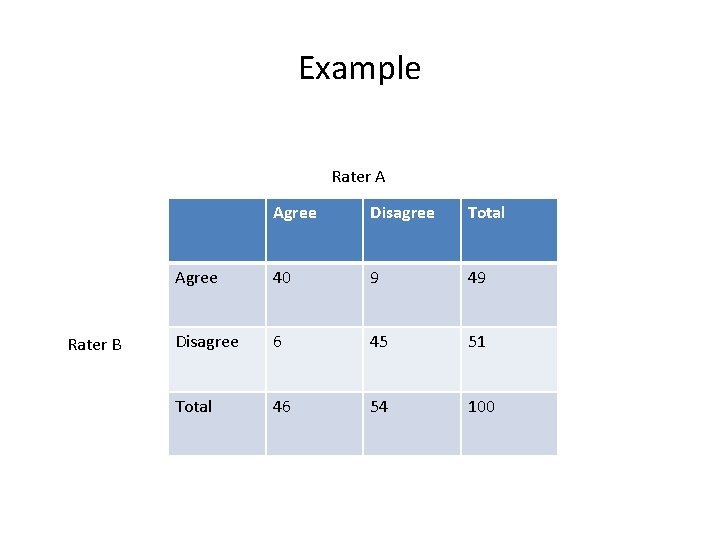
Example Rater A Rater B Agree Disagree Total Agree 40 9 49 Disagree 6 45 51 Total 46 54 100

• Here p = (40 + 45 ) / 100 = 0. 85 • p = (46/100)(49/100) + (54/100)(51/100)=0. 78 0 e • • Kappa statistics is graded broadly as follows: 0. 75 -1. 00 very good , 0. 41 – 0. 75 fair to good < 0. 40 poor Hence in the above analysis there is poor agreement