Intersection Testing Chapter 13 Tomas AkenineMller Department of

Intersection Testing Chapter 13 Tomas Akenine-Möller Department of Computer Engineering Chalmers University of Technology

What for? l l A tool needed for the graphics people all the time… Very important components: – l Finding if (and where) a ray hits an object – – l l Need to make them fast! Picking Ray tracing and global illumination For speed-up techniques Collision detection (treated in a later lecture) Tomas Akenine-Mőller © 2003

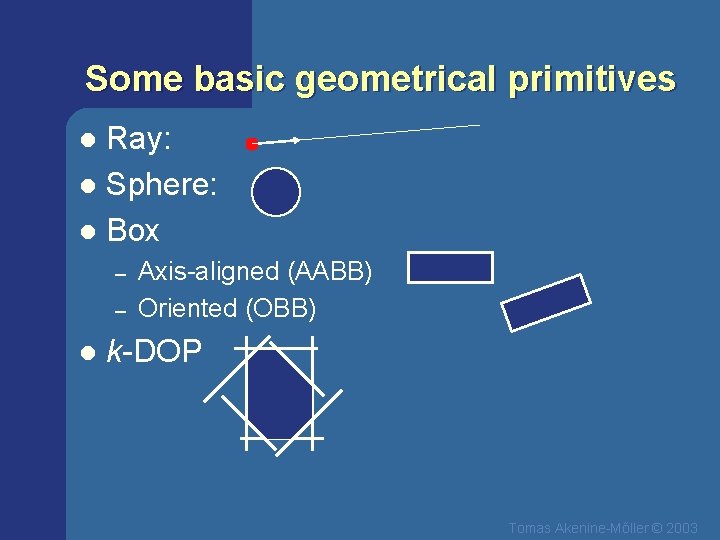
Some basic geometrical primitives Ray: l Sphere: l Box l – – l Axis-aligned (AABB) Oriented (OBB) k-DOP Tomas Akenine-Mőller © 2003

Four different techniques Analytical l Geometrical l Separating axis theorem (SAT) l Dynamic tests l l Given these, one can derive many tests quite easily – However, often tricks are needed to make them fast Tomas Akenine-Mőller © 2003

Analytical: Ray/sphere test d Sphere center: c, and radius r l Ray: r(t)=o+td l Sphere formula: ||p-c||=r l Replace p by r(t), and square it: l o r c Tomas Akenine-Mőller © 2003

Analytical, continued l o Be a little smart… d c Such tests are called ”rejection tests” l Other shapes: l Tomas Akenine-Mőller © 2003

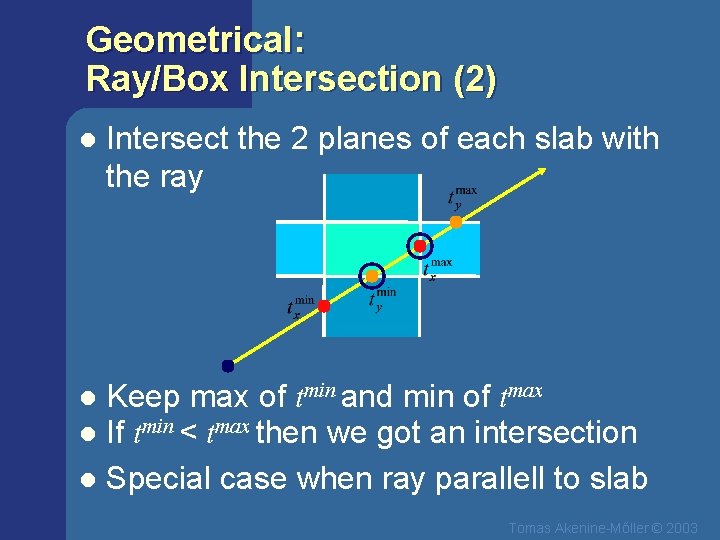
Geometrical: Ray/Box Intersection Boxes and spheres often used as bounding volumes l A slab is the volume between two parallell planes: l l A box is the logical intersection of three slabs (2 in 2 D): BOX Tomas Akenine-Mőller © 2003

Geometrical: Ray/Box Intersection (2) l Intersect the 2 planes of each slab with the ray Keep max of tmin and min of tmax If tmin < tmax then we got an intersection l Special case when ray parallell to slab l l Tomas Akenine-Mőller © 2003

Separating Axis Theorem (SAT) Page 563 in book l Two convex polyhedrons, A and B, are disjoint if any of the following axes separate the objects: – – – An axis orthogonal to a face of A An axis orthogonal to a face of B An axis formed from the cross product of one edge from each of A and B axis A and B overlaps on this axis Tomas Akenine-Mőller © 2003

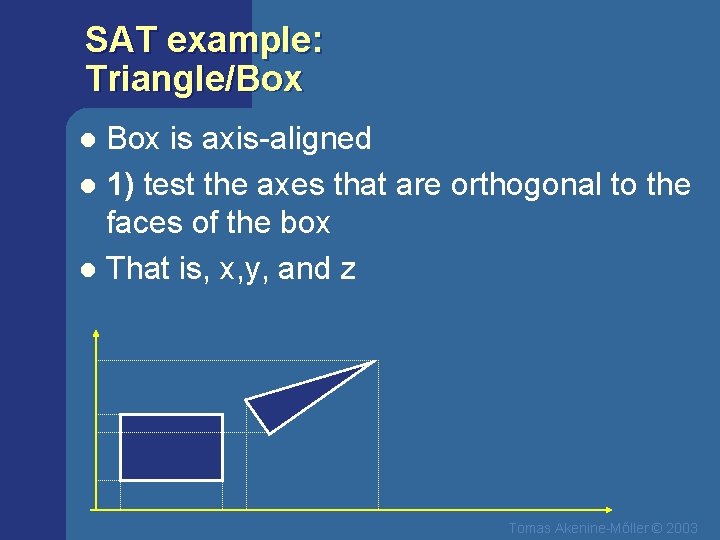
SAT example: Triangle/Box is axis-aligned l 1) test the axes that are orthogonal to the faces of the box l That is, x, y, and z l Tomas Akenine-Mőller © 2003

Triangle/Box with SAT (2) Assume that they overlapped on x, y, z l Must continue testing l 2) Axis orthogonal to face of triangle l axis Triangle seen from side Tomas Akenine-Mőller © 2003

Triangle/Box with SAT (3) If still no separating axis has been found… l 3) Test axis: t=ebox x etriangle l Example: l – – x-axis from box: ebox=(1, 0, 0) etriangle=v 1 -v 0 Test all such combinations l If there is at least one separating axis, then the objects do not collide l Else they do overlap l Tomas Akenine-Mőller © 2003

Rules of Thumb for Intersection Testing l Acceptance and rejection test – Try them early on to make a fast exit Postpone expensive calculations if possible l Use dimension reduction l – E. g. 3 one-dimensional tests instead of one complex 3 D test, or 2 D instead of 3 D Share computations between objects if possible l Timing!!! l Tomas Akenine-Mőller © 2003

Another analytical example: Ray/Triangle in detail v 2 Ray: r(t)=o+td v 1 l Triangle vertices: v 0, v 1, v 2 -v 0 v 1 -v 0 l A point in the triangle: v 0 =(1 l t(u, v)=v 0+u(v 1 - v 0 ) +v(v 2 - v 0 )= -u-v)v 0+uv 1+vv 2 [u, v>=0, u+v<=1] l Set t(u, v)=r(t), and solve! l Tomas Akenine-Mőller © 2003

Ray/Triangle (2) l Solve with Cramer’s rule: l Share factors to speed up computations Tomas Akenine-Mőller © 2003

Ray/Triangle (3) Implementation l Be smart! – Compute as little as possible then test l Examples: l Compute Then test valid bounds l if (v<0 or v>1) exit; l Tomas Akenine-Mőller © 2003

Point/Plane l Insert a point x into plane equation: Negative half space Positive half space origin Tomas Akenine-Mőller © 2003

Sphere/Plane AABB/Plane Sphere: compute l f (c) is the signed distance (n normalized) l abs( f (c)) > r no collision l abs( f (c)) = r sphere touches the plane l abs( f (c)) < r sphere intersects plane l Box: insert all 8 corners l If all f ’s have the same sign, then all points are on the same side, and no collision Tomas Akenine-Mőller © 2003 l

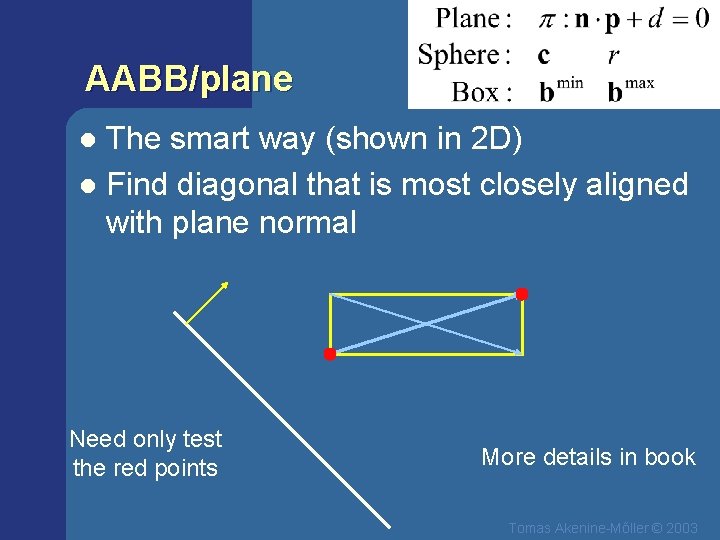
AABB/plane The smart way (shown in 2 D) l Find diagonal that is most closely aligned with plane normal l Need only test the red points More details in book Tomas Akenine-Mőller © 2003

Ray/Polygon: very briefly Intersect ray with polygon plane l Project from 3 D to 2 D l How? l Find max(|nx|, |ny|, |nz|) l Skip that coordinate! l Then, count crossing in 2 D l Tomas Akenine-Mőller © 2003

Volume/Volume tests Used in collision detection l Sphere/sphere l – l Axis-Aligned Bounding Box/AABB – l l Compute squared distance between sphere centers, and compare to (r 1+r 2)2 Test in 1 D for x, y, and z Oriented Bounding boxes Use SAT [details in book] Tomas Akenine-Mőller © 2003

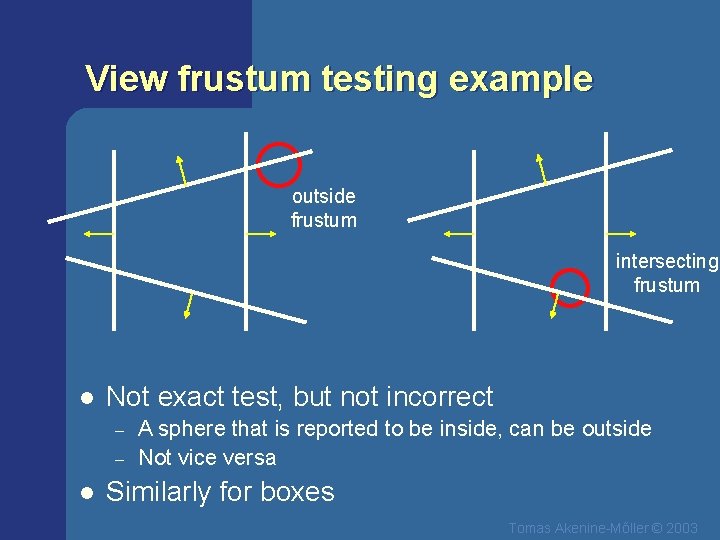
View frustum testing l l l View frustum is 6 planes: Near, far, right, left, top, bottom Create planes from projection matrix – – l Sphere/frustum common approach: – – l Let all positive half spaces be outside frustum Not dealt with here -- p. 613 -614 Test sphere against 6 frustum planes If in positive half space and r distances from plane => no intersection If intersecting plane or in negative half space, continue If not outside after all six planes, then inside or intersecting Example follows… Tomas Akenine-Mőller © 2003

View frustum testing example outside frustum intersecting frustum l Not exact test, but not incorrect – – l A sphere that is reported to be inside, can be outside Not vice versa Similarly for boxes Tomas Akenine-Mőller © 2003

Dynamic Intersection Testing [In book: 620 -628] Testing is often done every rendered frame, i. e. , at discrete time intervals l Therefore, you can get ”quantum effects” l Frame n+1 Dynamic testing deals with this l Is more expensive l Deals with a time interval: time between two frames Tomas Akenine-Mőller © 2003 l

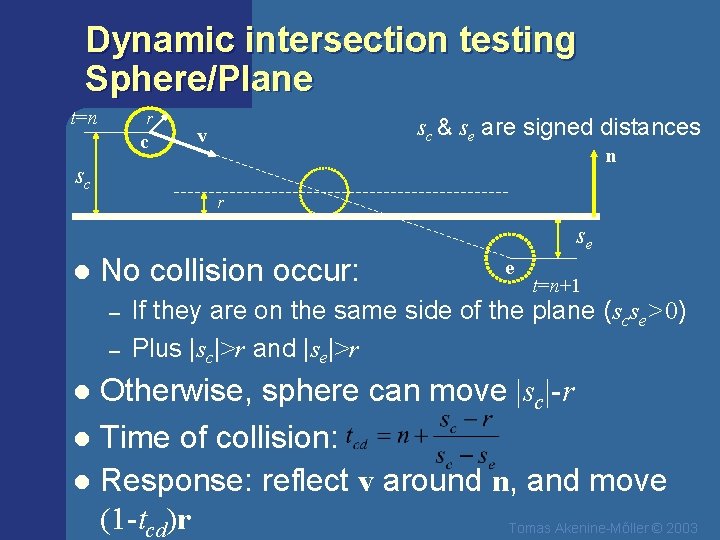
Dynamic intersection testing Sphere/Plane t=n r c sc l sc & se are signed distances v n r No collision occur: – – se e t=n+1 If they are on the same side of the plane (scse>0) Plus |sc|>r and |se|>r Otherwise, sphere can move |sc|-r l Time of collision: l Response: reflect v around n, and move (1 -tcd)r Tomas Akenine-Mőller © 2003 l

Dynamic Separating Axis Theorem l SAT: tests one axis at a time for overlap l Same with DSAT, but: – Need to adjust the projection on the axis so that the interval moves on the axis as well Need to test same axes as with SAT l Same criteria for overlap/disjoint: l – – If no overlap on axis => disjoint If overlap on all axes => objects overlap Tomas Akenine-Mőller © 2003