Intersection of a line and a verticalhorizontalprofile projection

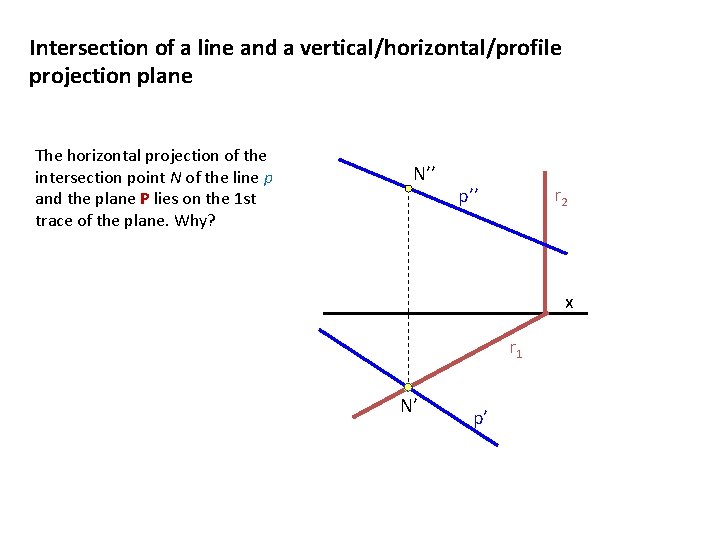
Intersection of a line and a vertical/horizontal/profile projection plane The horizontal projection of the intersection point N of the line p and the plane P lies on the 1 st trace of the plane. Why? N’’ r 2 p’’ x r 1 N’ p’

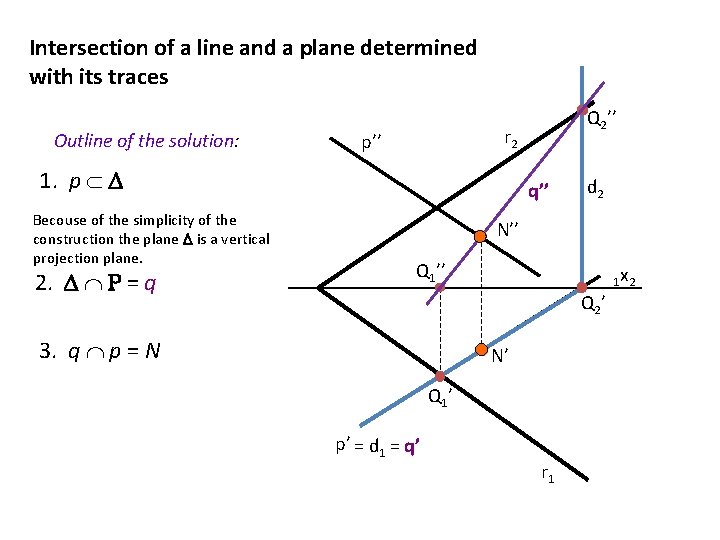
Intersection of a line and a plane determined with its traces Outline of the solution: r 2 p’’ 1. p Becouse of the simplicity of the construction the plane is a vertical projection plane. 2. = q Q 2’’ q’’ d 2 N’’ Q 1’’ 1 x 2 Q 2 ’ 3. q p = N N’ Q 1 ’ p’ = d 1 = q’ r 1

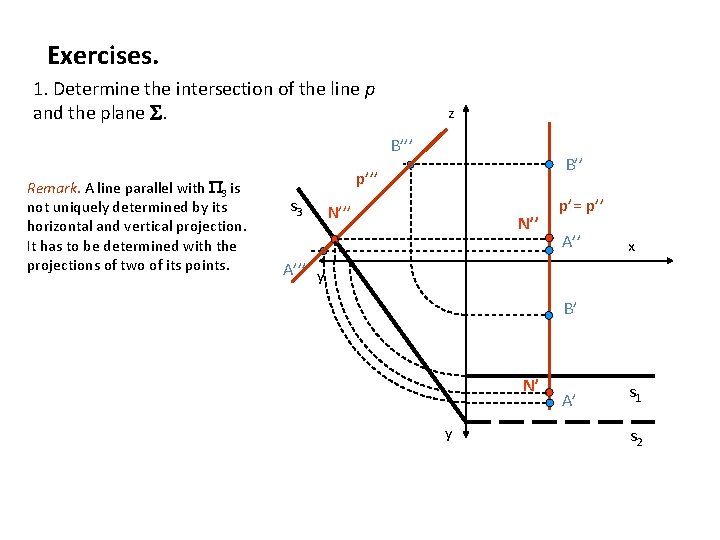
Exercises. 1. Determine the intersection of the line p and the plane . z B’’’ Remark. A line parallel with 3 is not uniquely determined by its horizontal and vertical projection. It has to be determined with the projections of two of its points. B’’ p’’’ s 3 N’’’ N’’ p’= p’’ A’’ x A’’’ y B’ N’ y A’ s 1 s 2

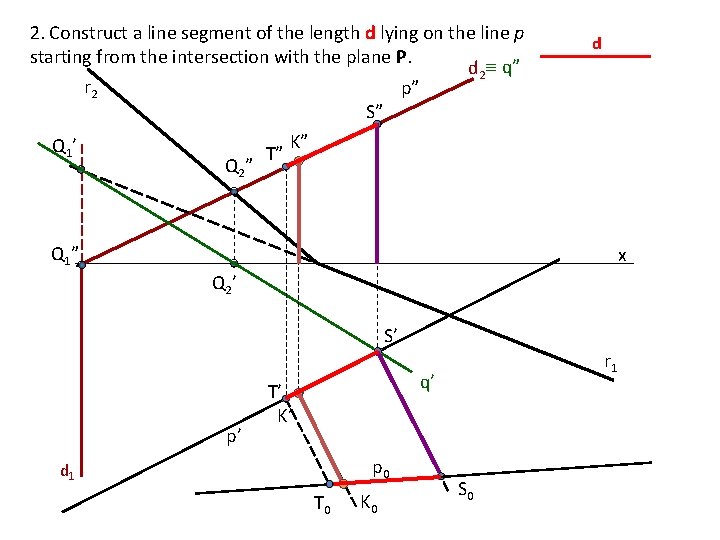
2. Construct a line segment of the length d lying on the line p starting from the intersection with the plane P. d 2 q” r 2 p” S” Q 1 ’ Q 2 ” T” d K” Q 1 ” x Q 2 ’ S’ p’ r 1 q’ T’ K’ p 0 d 1 T 0 K 0 S 0

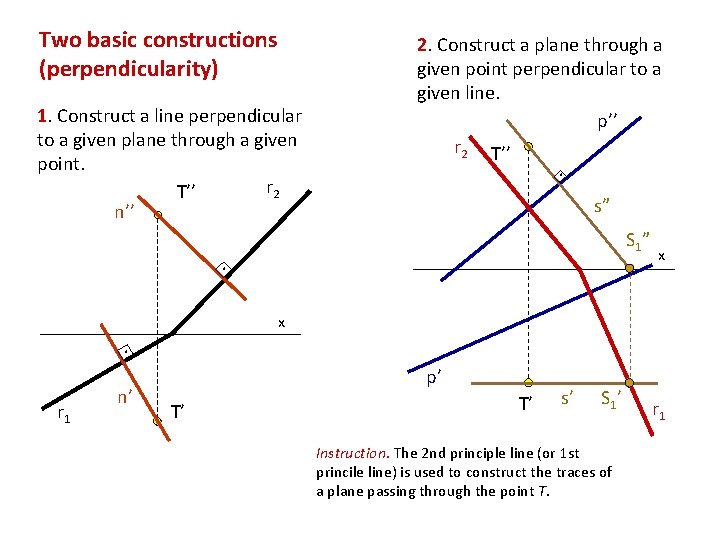
Two basic constructions (perpendicularity) 1. Construct a line perpendicular to a given plane through a given point. r 2 T’’ n’’ 2. Construct a plane through a given point perpendicular to a given line. p’’ r 2 T’’ . s” S 1 ” . x . r 1 n’ x p’ T’ T’ s’ S 1 ’ Instruction. The 2 nd principle line (or 1 st princile line) is used to construct the traces of a plane passing through the point T. r 1

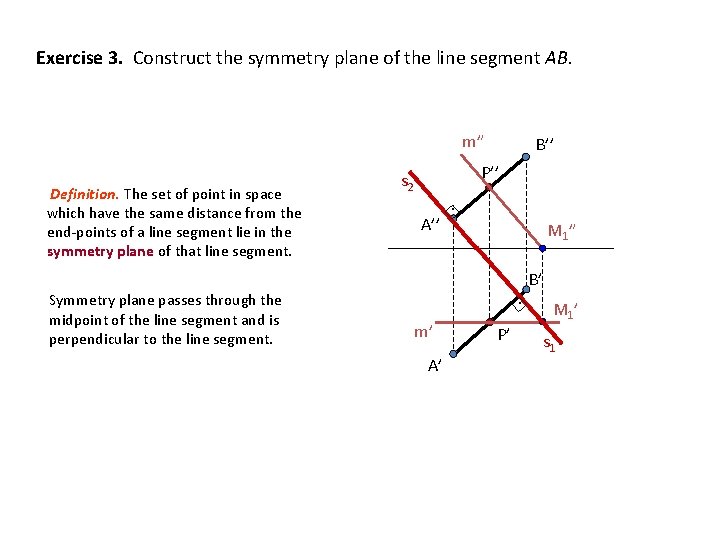
Exercise 3. Construct the symmetry plane of the line segment AB. m” Definition. The set of point in space which have the same distance from the end-points of a line segment lie in the symmetry plane of that line segment. Symmetry plane passes through the midpoint of the line segment and is perpendicular to the line segment. B’’ P’’ s 2 A’’ . M 1” . m’ A’ P’ B’ M 1’ s 1

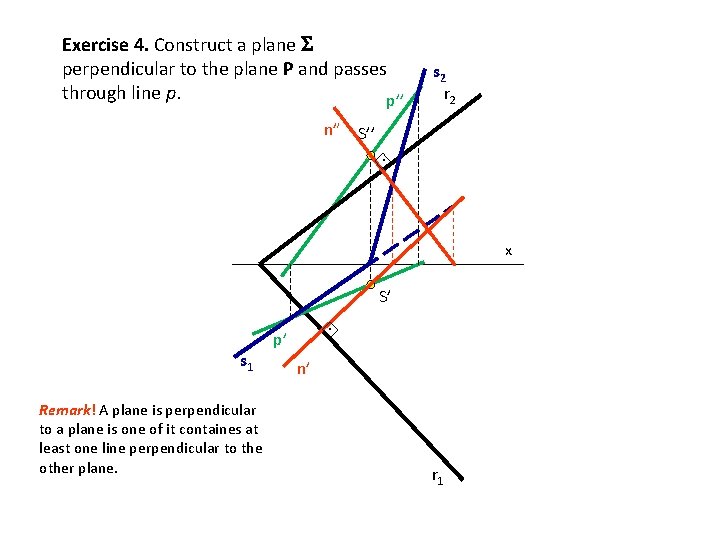
Exercise 4. Construct a plane perpendicular to the plane P and passes through line p. p’’ s 2 r 2 n” S’’. x S’ s 1 Remark! A plane is perpendicular to a plane is one of it containes at least one line perpendicular to the other plane. . p’ n’ r 1

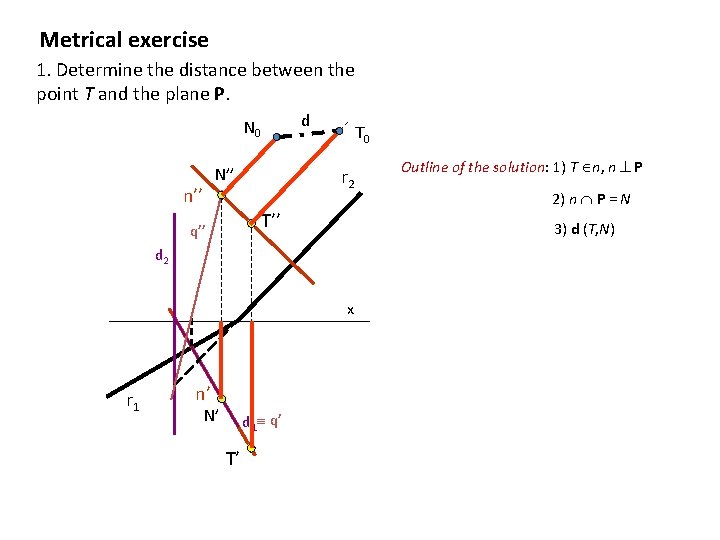
Metrical exercise 1. Determine the distance between the point T and the plane P. d N 0 n’’ N’’ T 0 r 2 T’’ q’’ x n’ N’ d 1 q’ T’ 2) n P = N 3) d (T, N) d 2 r 1 Outline of the solution: 1) T n, n P

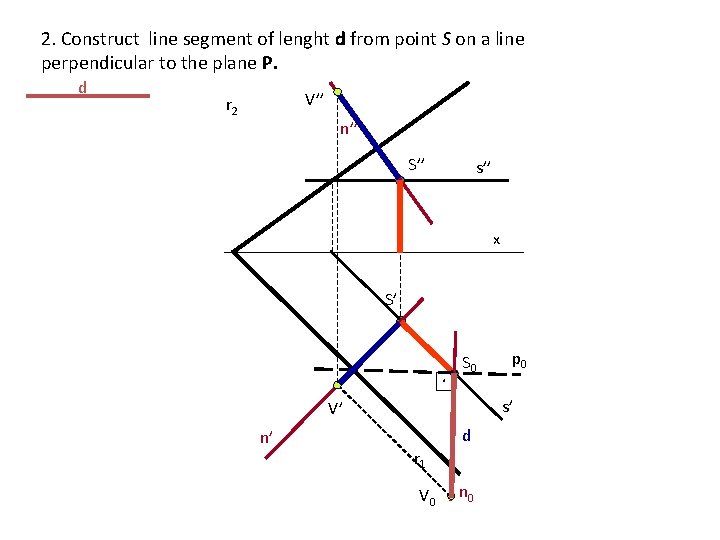
2. Construct line segment of lenght d from point S on a line perpendicular to the plane P. d V’’ r 2 n’’ S’’ s’’ x S’ . S 0 s’ V’ n’ p 0 d r 1 V 0 n 0

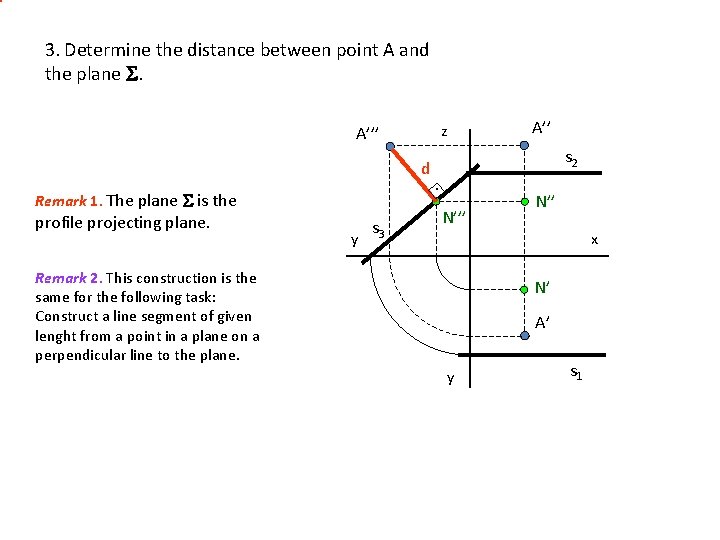
3. Determine the distance between point A and the plane . z A’’’ d Remark 1. The plane is the profile projecting plane. y s 3 A’’ s 2 . N’’’ N’’ x Remark 2. This construction is the same for the following task: Construct a line segment of given lenght from a point in a plane on a perpendicular line to the plane. N’ A’ y s 1

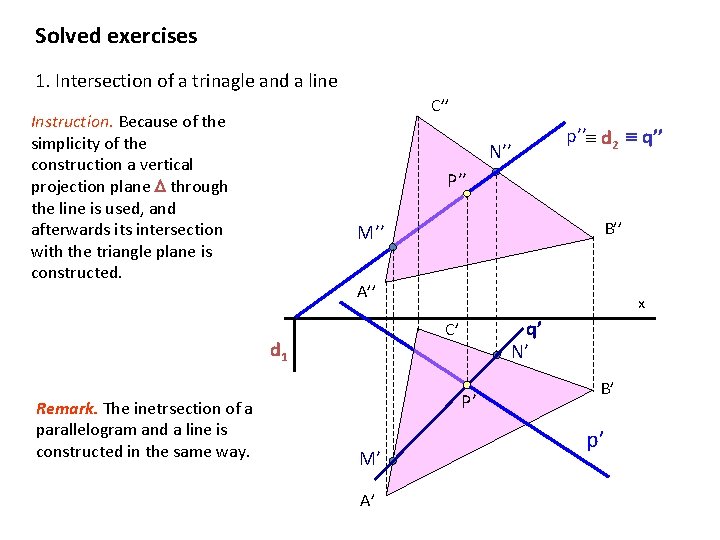
Solved exercises 1. Intersection of a trinagle and a line C’’ Instruction. Because of the simplicity of the construction a vertical projection plane through the line is used, and afterwards its intersection with the triangle plane is constructed. N’’ P’’ B’’ M’’ A’’ x q’ N’ C’ d 1 Remark. The inetrsection of a parallelogram and a line is constructed in the same way. p’’ d 2 q’’ P’ M’ A’ B’ p’

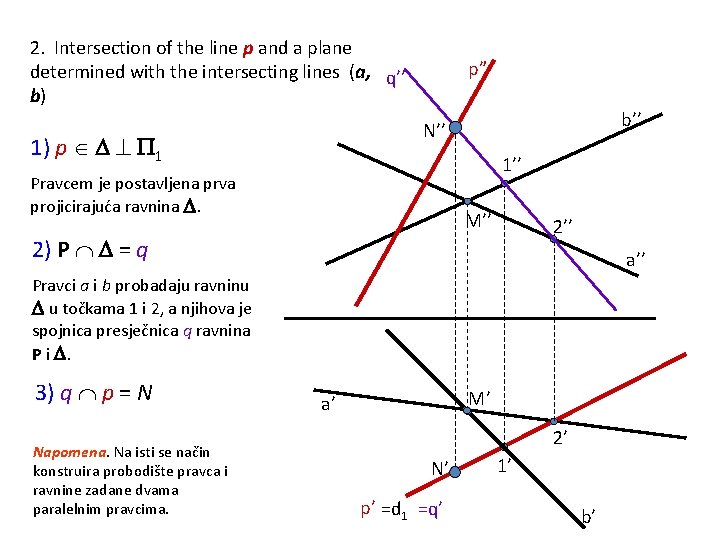
2. Intersection of the line p and a plane determined with the intersecting lines (a, q’’ b) p” b’’ N’’ 1) p 1 1’’ Pravcem je postavljena prva projicirajuća ravnina . M’’ 2) P = q a’’ Pravci a i b probadaju ravninu u točkama 1 i 2, a njihova je spojnica presječnica q ravnina P i . 3) q p = N Napomena. Na isti se način konstruira probodište pravca i ravnine zadane dvama paralelnim pravcima. M’ a’ 2’ N’ p’ =d 1 =q’ 1’ b’

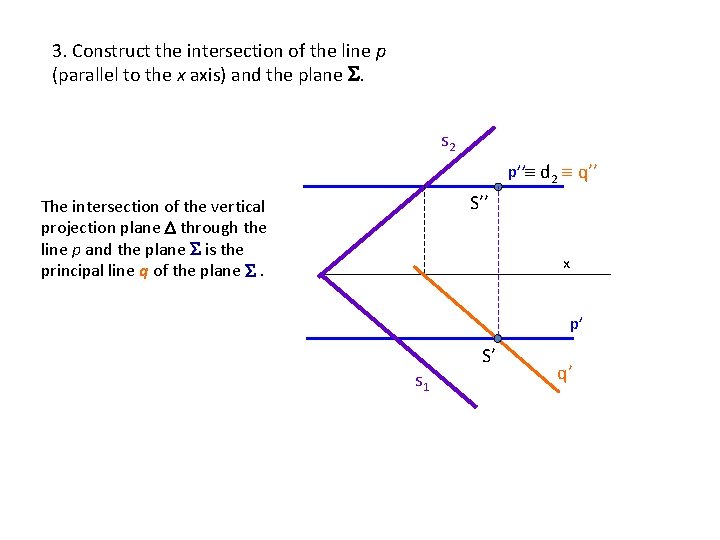
3. Construct the intersection of the line p (parallel to the x axis) and the plane . s 2 p’’ d 2 q’’ S’’ The intersection of the vertical projection plane through the line p and the plane is the principal line q of the plane . x p’ S’ s 1 q’

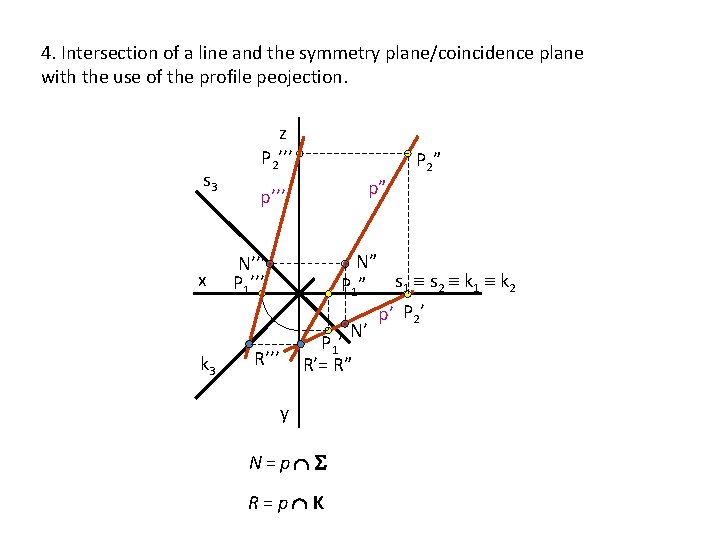
4. Intersection of a line and the symmetry plane/coincidence plane with the use of the profile peojection. s 3 x k 3 z P 2’’’ p” p’’’ P 2 ” N” P 1 ” s 1 s 2 k 1 k 2 p’ P 2’ N’ P 1 ’ R’= R” N’’’ P 1’’’ R’’’ y N=p R=p K

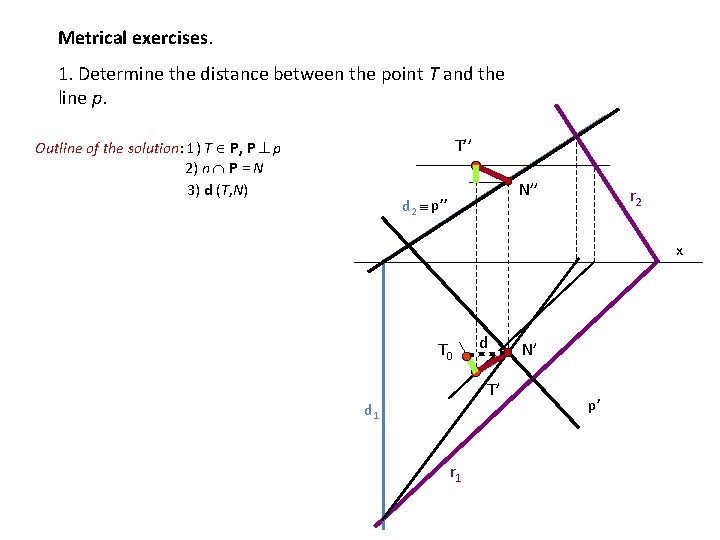
Metrical exercises. 1. Determine the distance between the point T and the line p. T’’ Outline of the solution: 1) T P, P p 2) n P = N 3) d (T, N) N’’ d 2 p’’ r 2 x T 0 d T’ d 1 r 1 N’ p’

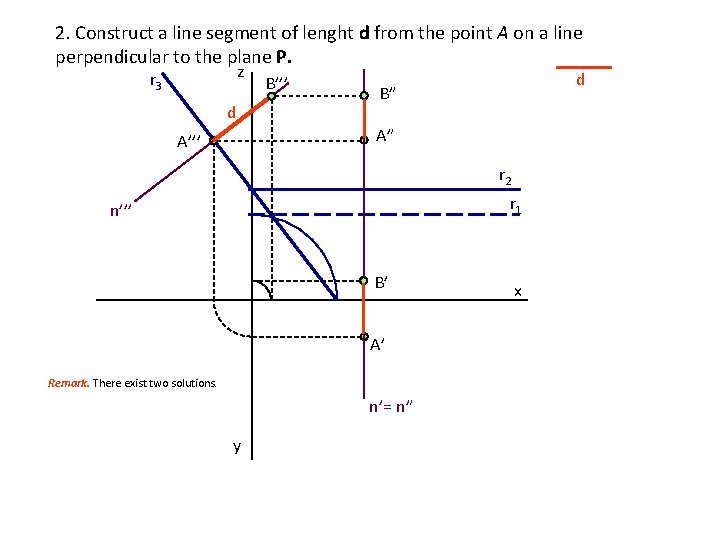
2. Construct a line segment of lenght d from the point A on a line perpendicular to the plane P. z r 3 d B’’’ d B” A” A’’’ r 2 r 1 n’’’ B’ A’ Remark. There exist two solutions. n’= n” y x