Interseco de Intervalos Sendo os intervalos conjuntos cujos

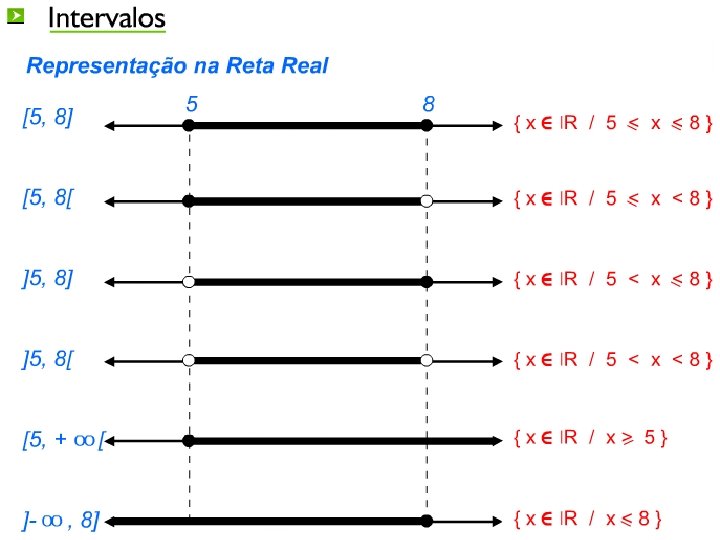
Intersecção de Intervalos Sendo os intervalos conjuntos, cujos elementos são números reais, é possível, quando temos dois ou mais intervalos, fazer a sua intersecção. A intersecção de dois intervalos, A e B, é por definição, um conjunto constituído pelos elementos comuns a A e a B.

Reunião de Intervalos A reunião de intervalos, A e B, é por definição um conjunto constituído pelos elementos que pertencem a A ou a B. Isto significa que para que um dado elemento pertença ao conjunto reunião basta que pertença a um dos conjuntos. Na prática, para obter a reunião de dois ou mais conjuntos o que fazemos é “juntar” os elementos dos conjuntos dados.

Intersecção e Reunião Intervalos Exemplo 1 Consideremos os intervalos e Determine a intersecção e a união de A e B.

Intersecção e União de Intervalos Exemplo 2 Sejam e Determine a intersecção e a união de A e B.

Intersecção de Intervalos Exemplo 3 Dados os intervalos e encontremos a sua intersecção. A representação gráfica é Neste caso o único elemento comum aos dois intervalos é o Logo,

Intersecção de Intervalos Exemplo 4 Dados os intervalos intersecção dos dois intervalos. e procuremos a A representação gráfica é Agora não existem elementos que pertençam simultaneamente aos dois intervalos já que o pertence a mas não pertence a. Assim,

Intersecção de Intervalos Exemplo 5 Dados os intervalos intersecção dos dois intervalos. A representação gráfica é Neste caso temos Logo, Assim, , e procuremos a

Reunião de Intervalos Exemplo 1 Consideremos os intervalos e Comecemos por fazer a representação gráfica de Assim, e .

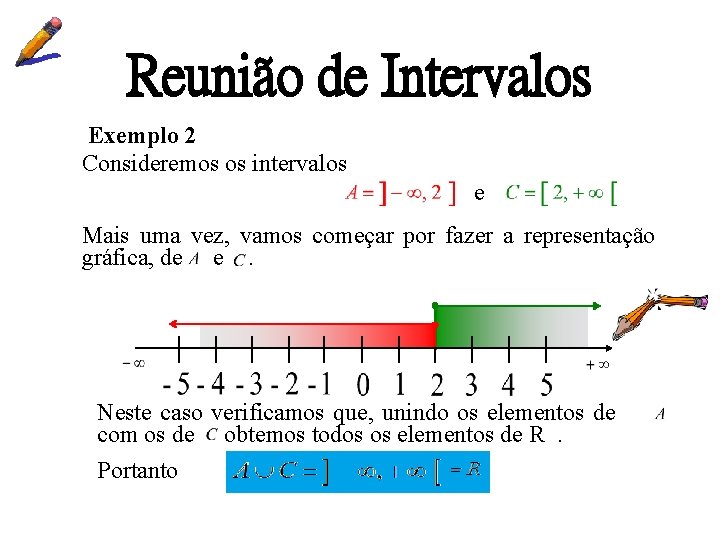
Reunião de Intervalos Exemplo 2 Consideremos os intervalos e Mais uma vez, vamos começar por fazer a representação gráfica, de e. Neste caso verificamos que, unindo os elementos de com os de obtemos todos os elementos de R. Portanto

Reunião de Intervalos Exemplo 3 Consideremos os intervalos e A representação gráfica destes dois intervalos é. A intersecção dos intervalos e é o conjunto vazio. Não nos é possível representar esta reunião sob a forma de um único intervalo.

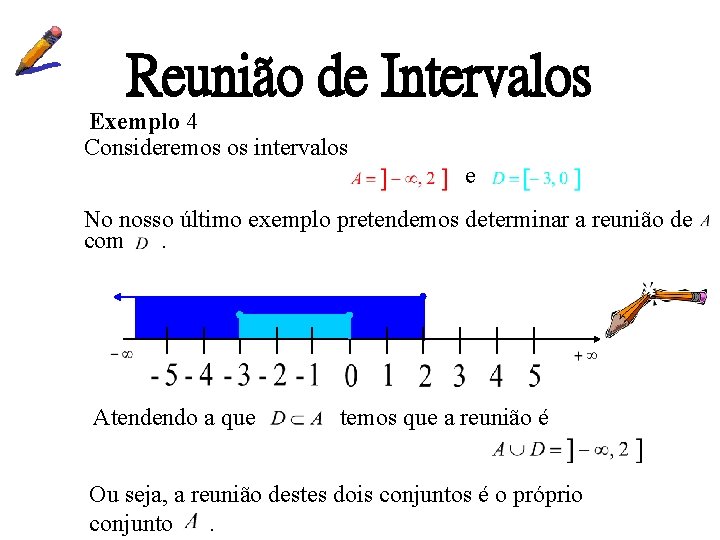
Reunião de Intervalos Exemplo 4 Consideremos os intervalos e No nosso último exemplo pretendemos determinar a reunião de com. Atendendo a que temos que a reunião é Ou seja, a reunião destes dois conjuntos é o próprio conjunto.