INTERPRETING REGRESSION COEFFICIENTS OUTLINE 1 2 3 4

OUTLINE 1. 2. 3. 4. 5. 6. 7. Back to Basics Form: The Regression

BACK TO BASIC CONCEPTS PRE = (E 1 – E 2)/E 1 = 1

E 2 = Σ (Yi – Ŷ)2 that is, sum of squared differences between

STRENGTH OF ASSOCIATION Symbol = r 2 = PRE = (E 1 – E

FOCUSING ON FORM As given by equation Ŷi = a + b. Xi Constant

THE CORRELATION COEFFICIENT Symbol = r Summary statement of form (from sign) and indirect

ON THE CORRELATION COEFFICIENT r Analogous to slope b (with removal of intercept a)

LOOKING AHEAD: MEASURING SIGNIFICANCE 1. Testing the null hypothesis: F = r 2(n-2)/(1 -r

Coefficients for Regression of N Electoral Democracies (Y) on Change Over Time (X): a

Interpreting the Equation • N democracies = - 1. 427 +. 126 year •

Example 2: Wine and Heart Disease Data in Lectures 5 -6 X = per

Slides: 16

Download presentation

INTERPRETING REGRESSION COEFFICIENTS

OUTLINE 1. 2. 3. 4. 5. 6. 7. Back to Basics Form: The Regression Equation Strength: PRE and r 2 The Correlation Coefficient r Significance: Looking Ahead Example 1: Democracy in Latin America Example 2: Wine Consumption and Heart Disease

BACK TO BASIC CONCEPTS PRE = (E 1 – E 2)/E 1 = 1 – E 2/E 1 = Σ(Y – Y)2 Rule for “predicting” values of Y, given knowledge of X: Yhati = a + b. Xi

E 2 = Σ (Yi – Ŷ)2 that is, sum of squared differences between observed values of Y and predicted values of Y (values of Y as “predicted” by the regression equation) Thus the elements of PRE.

STRENGTH OF ASSOCIATION Symbol = r 2 = PRE = (E 1 – E 2)/E 1 = (total variance – unexplained variance)/total variance Varies from 0 to 1 Some back-of-the-envelope thresholds: 0. 10, 0. 30, 0. 50+

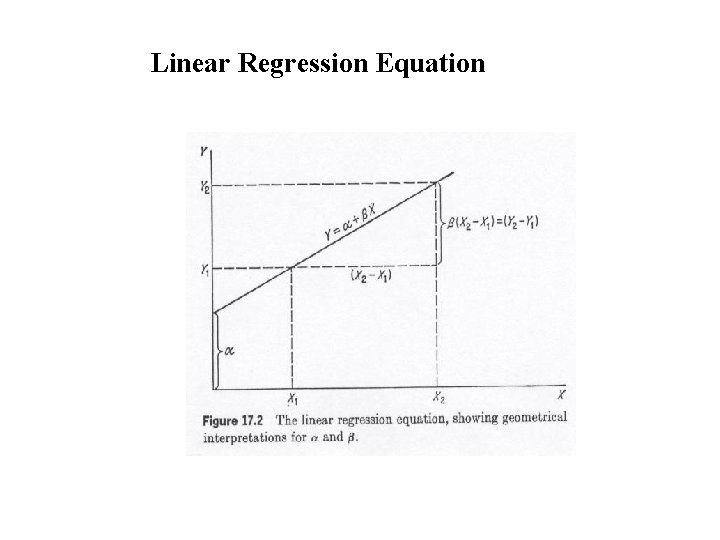
FOCUSING ON FORM As given by equation Ŷi = a + b. Xi Constant a = intercept = predicted value of Y when X = 0 Coefficient b = slope = average change in Y for change in X • Magnitude (large or small) • Sign (positive or negative) • Key to much interpretation

Linear Regression Equation

THE CORRELATION COEFFICIENT Symbol = r Summary statement of form (from sign) and indirect statement of strength r = square root of r 2, varies from – 1 to +1 subject to over-interpretation useful for preliminary assessment of association Symmetrical no matter which variable is X and which is Y (note: slope b is not symmetrical)

ON THE CORRELATION COEFFICIENT r Analogous to slope b (with removal of intercept a) The “standardized regression coefficient, ” or beta weight: β= b (stand. dev. X/stand. dev. Y) employs slope, values, and dispersion of variables thus a “standardized” slope Question: How much action on Y do you get from X? In bivariate (or “simple”) regression, β = r

LOOKING AHEAD: MEASURING SIGNIFICANCE 1. Testing the null hypothesis: F = r 2(n-2)/(1 -r 2) 2. Standard errors and confidence intervals: Dependent on desired significance level Bands around the regression line 95% confidence interval ± 1. 96 x SE

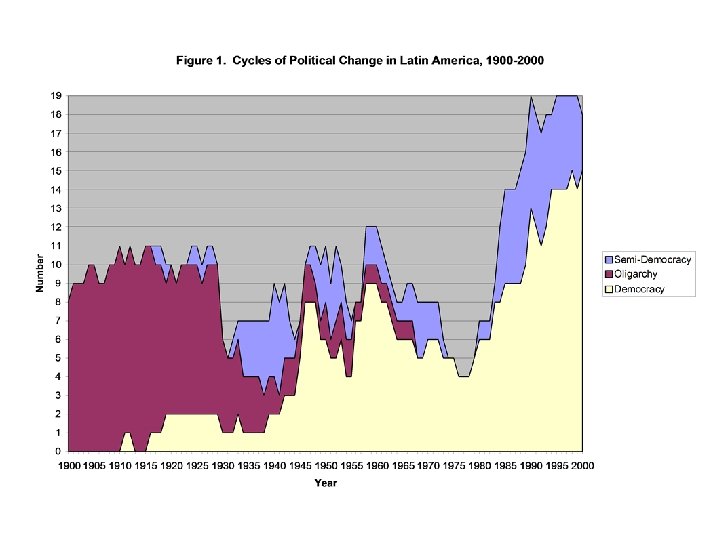
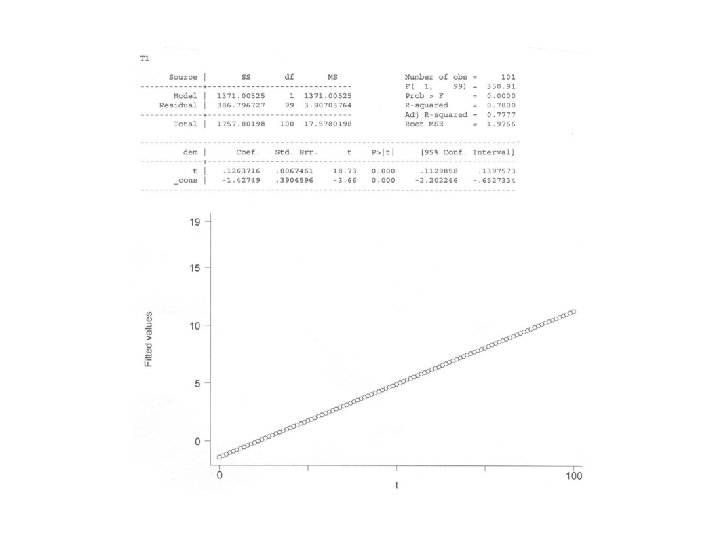
Coefficients for Regression of N Electoral Democracies (Y) on Change Over Time (X): a = -1. 427 b = +. 126 r = +. 883 r 2 =. 780, Adjusted r 2 =. 777 Standard error of slope =. 0067 95% confidence interval for slope = (. 0067)x 1. 96 = ±. 0013 setting confidence bands at. 113 and. 140 F for equation = 350. 91, p < 0. 000

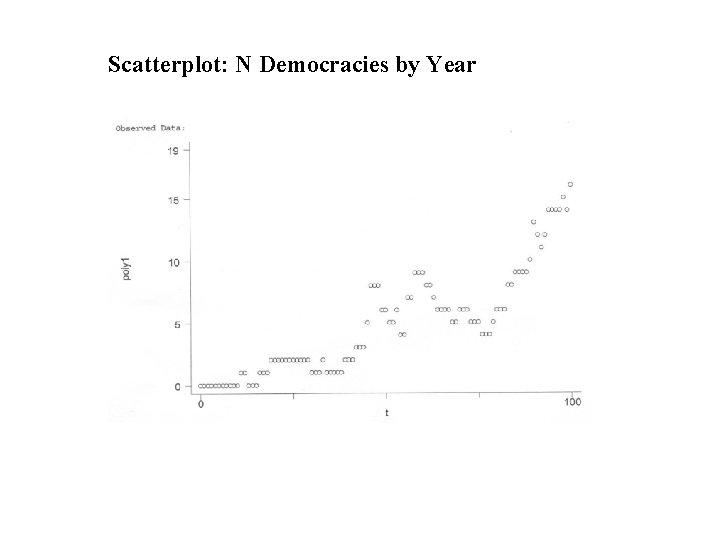
Scatterplot: N Democracies by Year

Interpreting the Equation • N democracies = - 1. 427 +. 126 year • intercept = nonsense, but allows calculation of year that predicted value of Y would be zero, in this case 1910 • slope = +. 126 so, one additional democracy every eight years • and by 2000, total 11 -12 democracies • PRE =. 777

Example 2: Wine and Heart Disease Data in Lectures 5 -6 X = per capita annual consumption of alcohol from wine, in liters Y = deaths from heart disease, per 100, 000 people Equation: Ŷ = 260. 6 - 22. 97 X r = - 0. 843 What’s the interpretation?