Interpreting Basic Statistics Beginners statistics for assessing the

Interpreting Basic Statistics Beginners’ statistics for assessing the effectiveness of an intervention UH Bristol library service

Aim To give you a greater understanding of how to interpret basic medical statistics. Session outline: • Statistics which compare risks • Statistics which test confidence • Forest Plots

Objectives • Use raw data to calculate simple statistics to compare risk • Interpret p-values and confidence intervals within the context of a study • Pick out key information from a forest plot • Understand the values and issues of using different statistical measures

Statistics Which Compare Risk

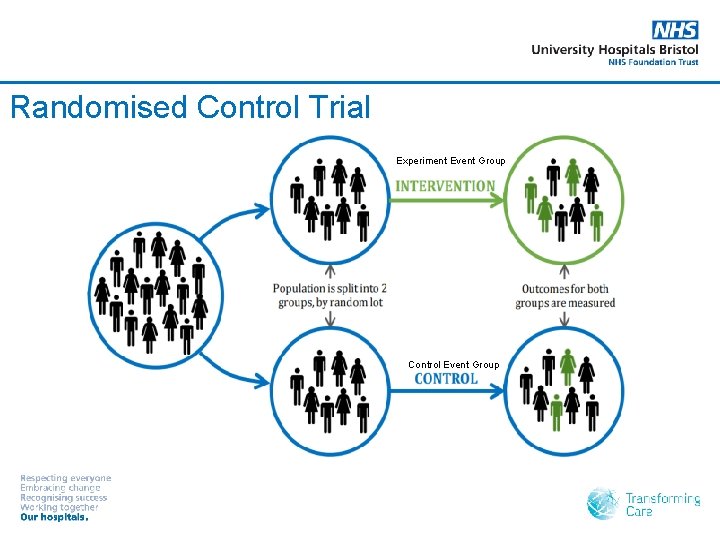
Randomised Control Trial Experiment Event Group Control Event Group

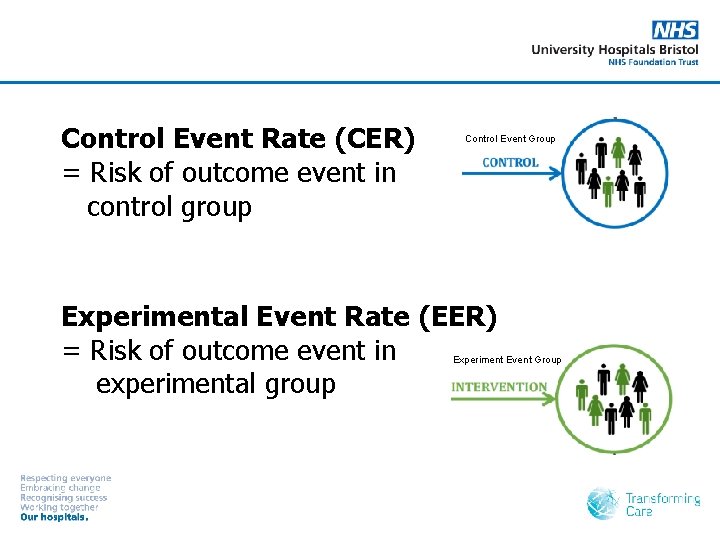
Control Event Rate (CER) = Risk of outcome event in control group Control Event Group Experimental Event Rate (EER) = Risk of outcome event in experimental group Experiment Event Group

Example 1 Randomised Control Trial of a new drug tested on a population at risk of a heart attack. § 90/100 of those not receiving the drug (control group) will have a heart attack. § 60/100 of those receiving the drug (experimental group) will have a heart attack.

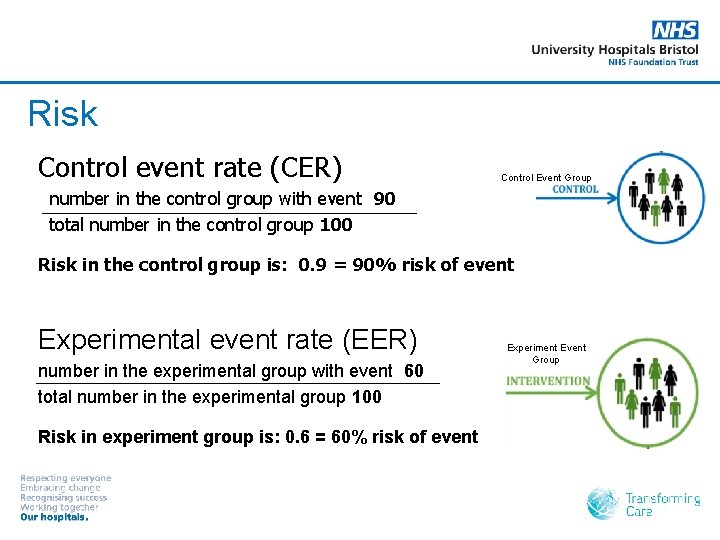
Risk Control event rate (CER) Control Event Group number in the control group with event 90 total number in the control group 100 Risk in the control group is: 0. 9 = 90% risk of event Experimental event rate (EER) number in the experimental group with event 60 total number in the experimental group 100 Risk in experiment group is: 0. 6 = 60% risk of event Experiment Event Group

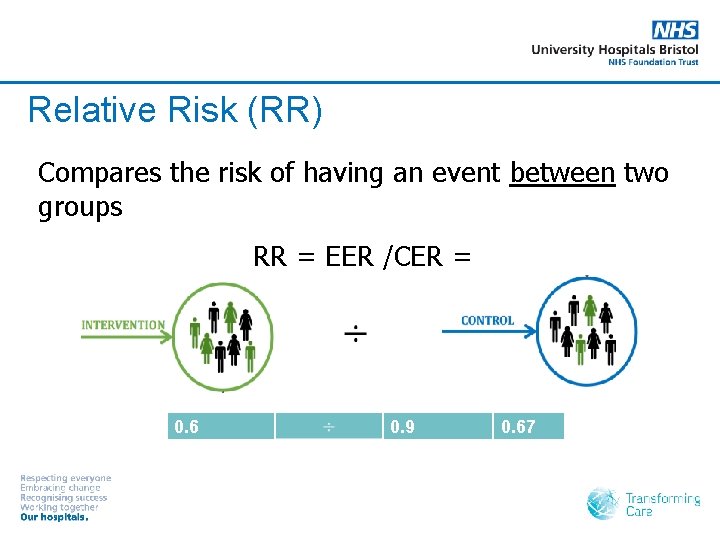
Relative Risk (RR) Compares the risk of having an event between two groups RR = EER /CER = 0. 6 0. 9 0. 67

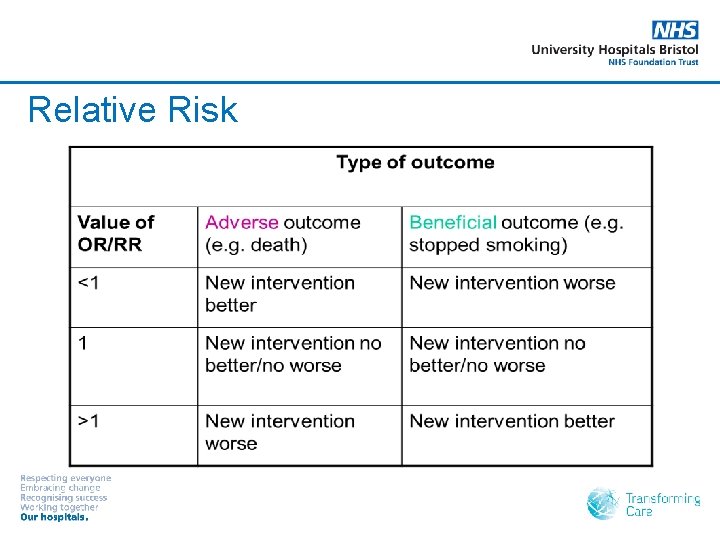
Relative Risk

Example 2 2 RCTs of a new drug tested on two populations at risk of a heart attack over 10 years. RCT 1: High risk group (n=200) § 90/100 of those not receiving the drug (control group) will have a heart attack. § 60/100 of those receiving the drug (experimental group) will have a heart attack. RCT 2: Low risk group (n=200) § 3/100 of those not receiving the drug (control group) will have a heart attack. § 2/100 of those receiving the drug (experimental group) will have a heart attack.

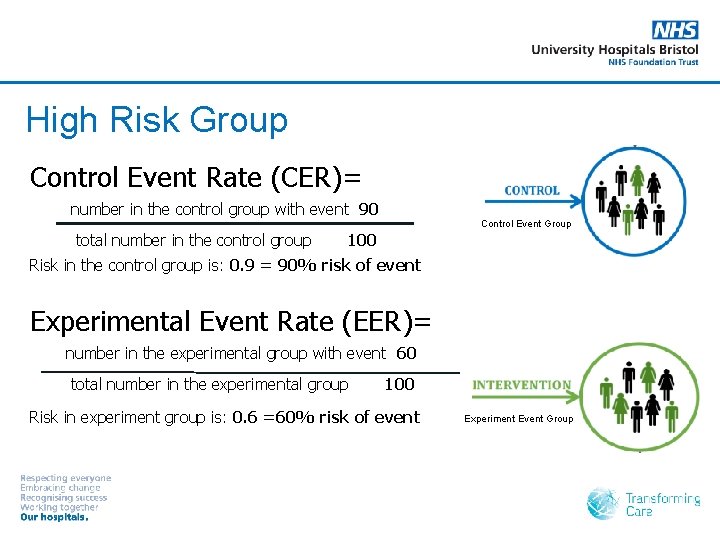
High Risk Group Control Event Rate (CER)= number in the control group with event 90 total number in the control group Control Event Group 100 Risk in the control group is: 0. 9 = 90% risk of event Experimental Event Rate (EER)= number in the experimental group with event 60 total number in the experimental group 100 Risk in experiment group is: 0. 6 =60% risk of event Experiment Event Group

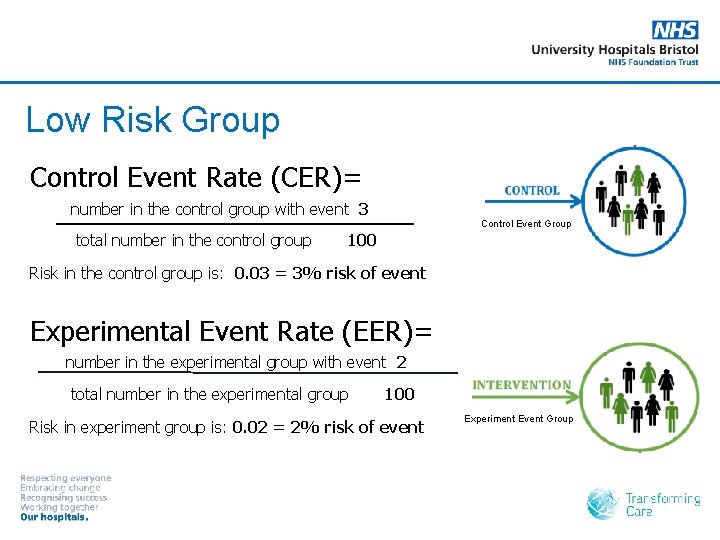
Low Risk Group Control Event Rate (CER)= number in the control group with event 3 total number in the control group Control Event Group 100 Risk in the control group is: 0. 03 = 3% risk of event Experimental Event Rate (EER)= number in the experimental group with event 2 total number in the experimental group 100 Risk in experiment group is: 0. 02 = 2% risk of event Experiment Event Group

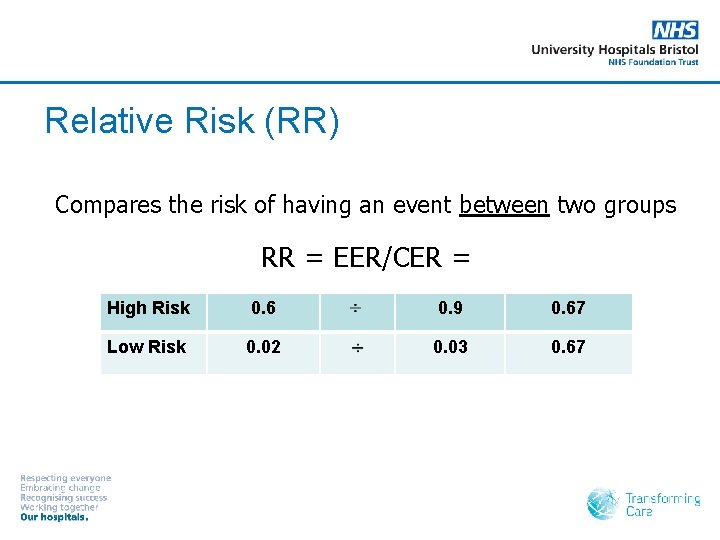
Relative Risk (RR) Compares the risk of having an event between two groups RR = EER/CER = High Risk 0. 6 0. 9 0. 67 Low Risk 0. 02 0. 03 0. 67

Relative Risk Reduction (RRR) The reduction in the rate of the event in the treatment group relative to the control group RRR = 1 – RR = High Risk 1 - 0. 67 = 0. 33 = 33% Low risk 1 - 0. 67 = 0. 33 = 33%

Absolute Risk Reduction (or Risk Difference) Compares the risk of having an event between two groups ARR = CER – EER = High Risk 0. 9 - 0. 6 = 0. 3 30% Low Risk 0. 03 - 0. 02 = 0. 01 1% RRR 33%

Example If you didn't take aspirin, your risk of having a heart attack was 2% over 5 years. If you did take aspirin, your risk of having a heart attack was 1% over 5 years. Relative Risk Reduction would say that aspirin reduces your chance of heart attack by 50% Absolute Risk Reduction would say that aspirin reduced your chance of heart attack by 1%

Numbers Needed to Treat (NNT) The number of people who must be treated to result in benefit in one person. It is the inverse of ARR. NNT = 1/ARR =

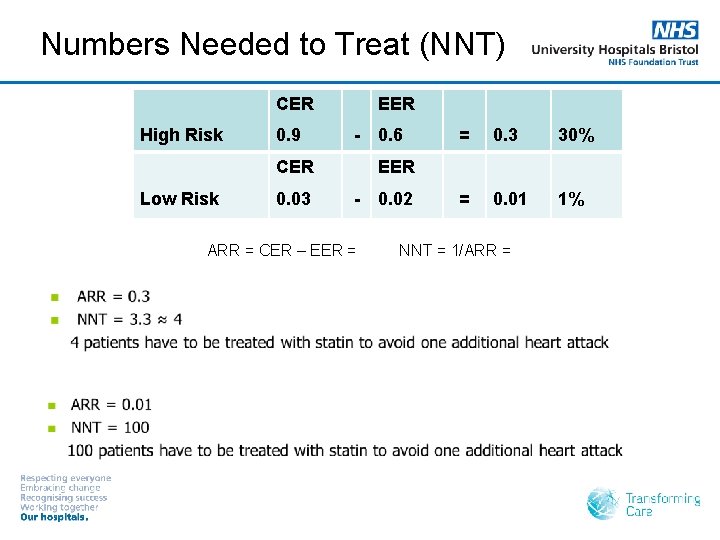
Numbers Needed to Treat (NNT) CER High Risk 0. 9 EER - CER Low Risk 0. 03 0. 6 = 0. 3 30% = 0. 01 1% EER - ARR = CER – EER = 0. 02 NNT = 1/ARR =

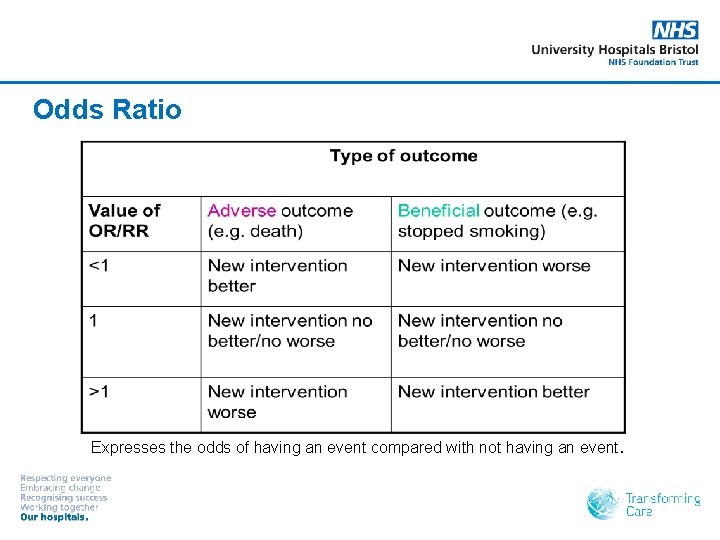
Odds Ratio Expresses the odds of having an event compared with not having an event.

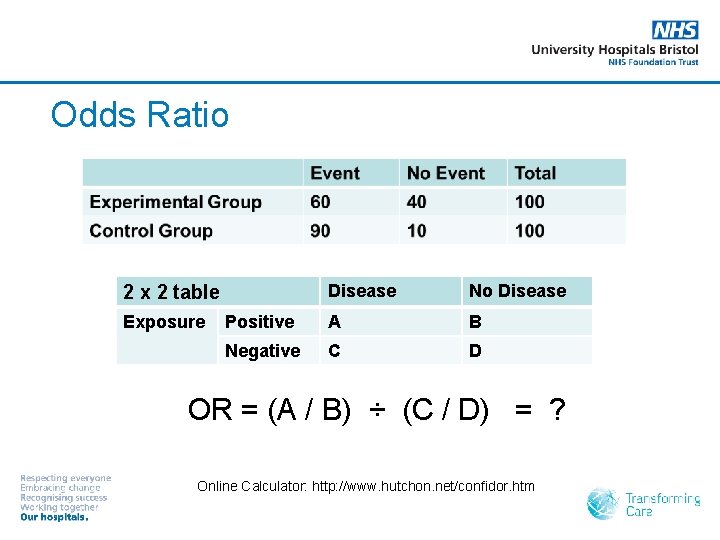
Odds Ratio Disease No Disease Positive A B Negative C D 2 x 2 table Exposure OR = (A / B) ÷ (C / D) = ? Online Calculator: http: //www. hutchon. net/confidor. htm

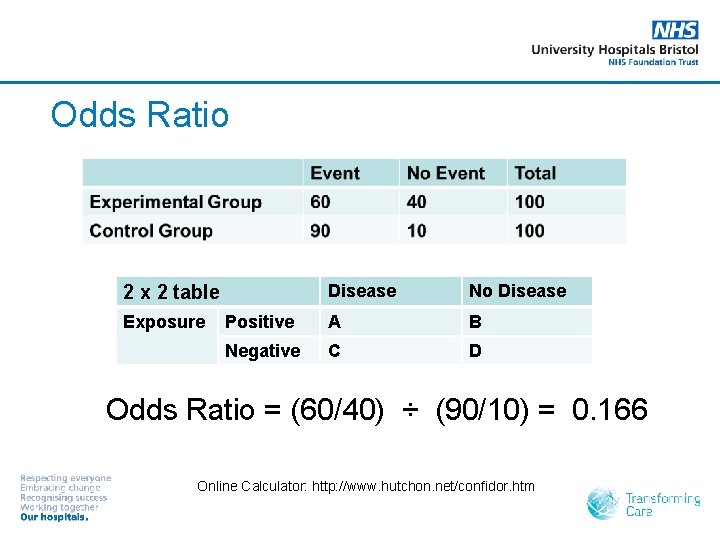
Odds Ratio Disease No Disease Positive A B Negative C D 2 x 2 table Exposure Odds Ratio = (60/40) ÷ (90/10) = 0. 166 Online Calculator: http: //www. hutchon. net/confidor. htm

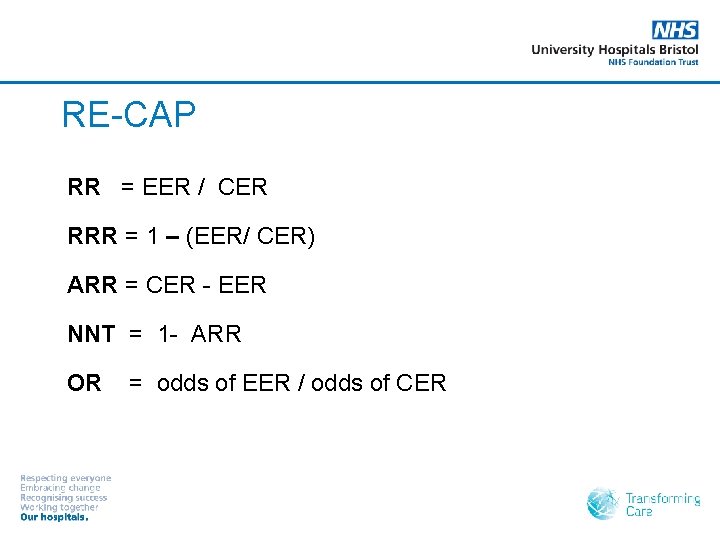
RE-CAP RR = EER / CER RRR = 1 – (EER/ CER) ARR = CER - EER NNT = 1 - ARR OR = odds of EER / odds of CER

Statistics Which Test Confidence

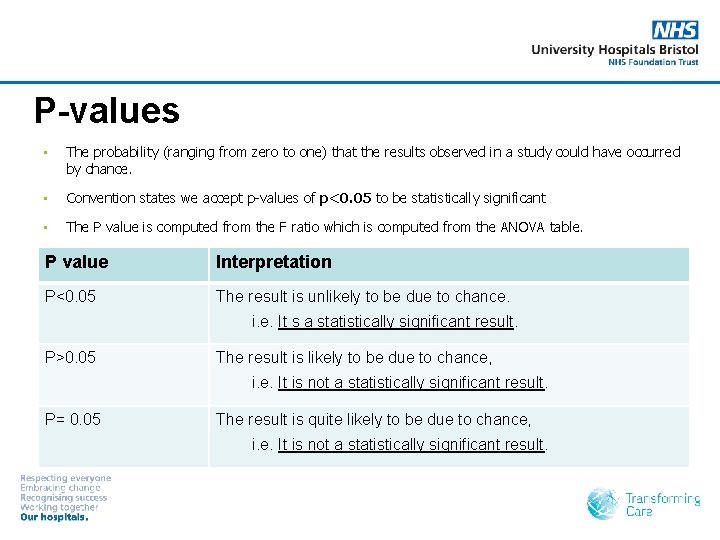
P-values • The probability (ranging from zero to one) that the results observed in a study could have occurred by chance. • Convention states we accept p-values of p<0. 05 to be statistically significant • The P value is computed from the F ratio which is computed from the ANOVA table. P value Interpretation P<0. 05 The result is unlikely to be due to chance. i. e. It s a statistically significant result. P>0. 05 The result is likely to be due to chance, i. e. It is not a statistically significant result. P= 0. 05 The result is quite likely to be due to chance, i. e. It is not a statistically significant result.

Confidence Intervals What is a confidence interval? • The range within which we can be 95% sure that the true value for the whole population lies What can a confidence interval indicate? • • • Indication of precision Strength of the evidence Whether a result is statistically significant

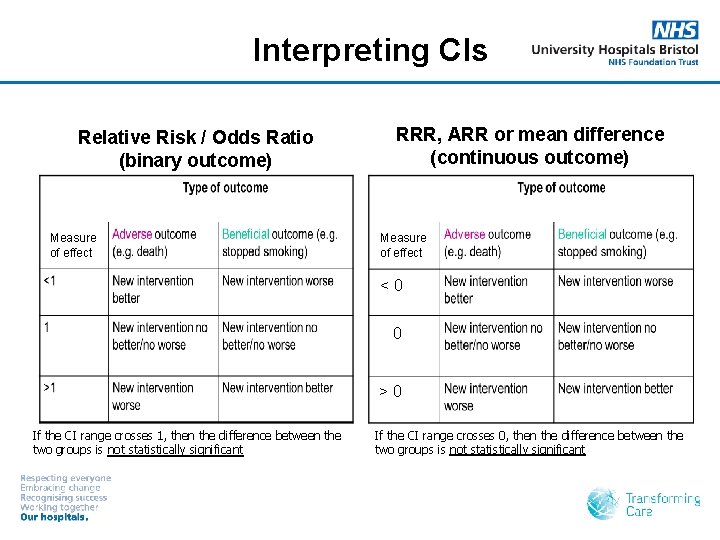
Interpreting CIs Relative Risk / Odds Ratio (binary outcome) Measure of effect RRR, ARR or mean difference (continuous outcome) Measure of effect < 0 0 > 0 If the CI range crosses 1, then the difference between the two groups is not statistically significant If the CI range crosses 0, then the difference between the two groups is not statistically significant

Trials to examine the effect of probiotics on the risk of antibiotic associated diarrhoea • Which study/studies show a significant result? • Which study demonstrated the strongest evidence?

Forest Plots

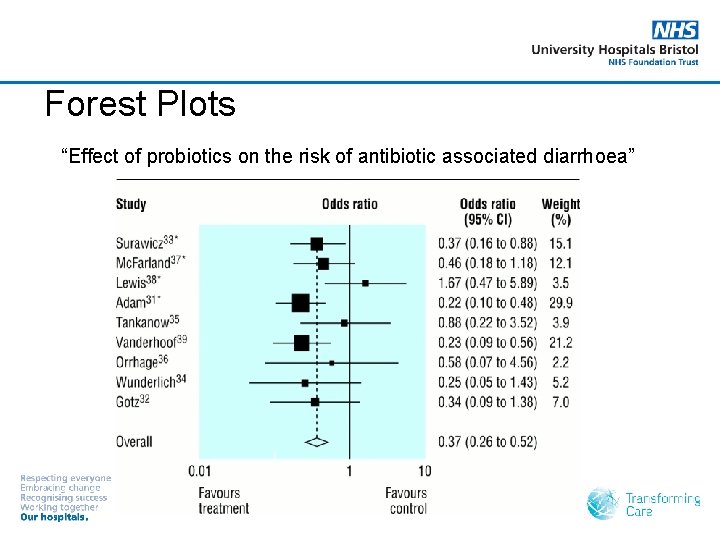
Forest Plots “Effect of probiotics on the risk of antibiotic associated diarrhoea”

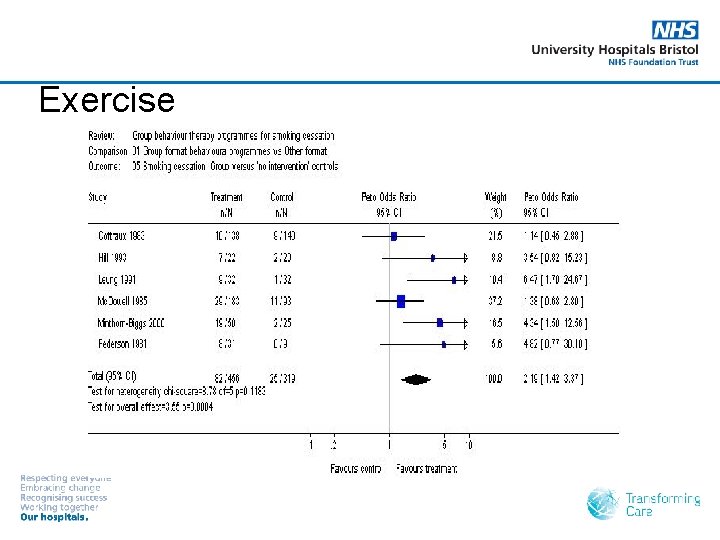
Exercise

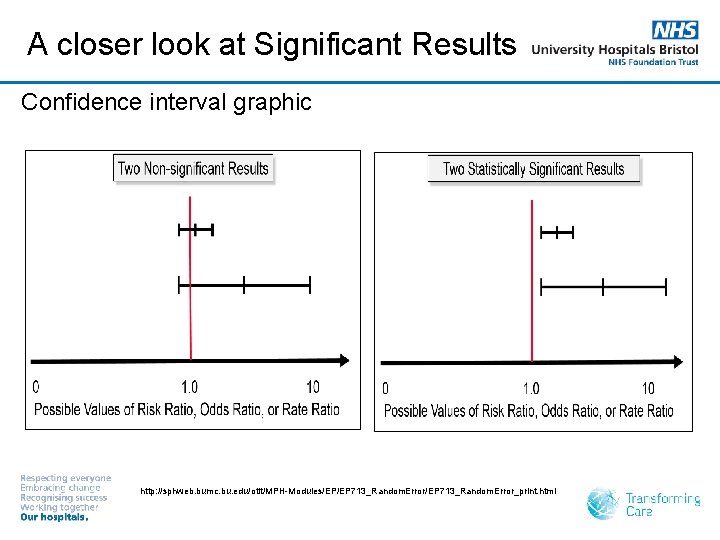
A closer look at Significant Results Confidence interval graphic http: //sphweb. bumc. bu. edu/otlt/MPH-Modules/EP/EP 713_Random. Error_print. html

Library outreach service The library Level 5, Education Centre Upper Maudlin St Tel. ext. 20105 Email. library@uhbristol. nhs. uk