Interpretational Applications of Spectral Decomposition Greg Partyka James

Spectral Decomposition • uses the discrete Fourier transform to: – quantify thin-bed interference, and

Outline • • Convolutional Model Implications Wedge Model Response The Tuning Cube Spectral Balancing

Long Window Analysis • The geology is unpredictable. • Its reflectivity spectrum is therefore

Long Window Analysis Wavelet w(t) Noise n(t) Amplitude Seismic Trace s(t) Travel Time Reflectivity

Short Window Analysis • The non-random geology locally filters the reflecting wavelet. • Its

Short Window Analysis Wavelet w(t) Noise n(t) Amplitude Seismic Trace s(t) Travel Time Reflectivity

Spectral Interference • The spectral interference pattern is imposed by the distribution of acoustic

Spectral Interference Source Wavelet Amplitude Spectrum Source Wavelet Reflected Thin Bed Wavelets Reflection Thin

SPECTRAL AMPLITUDES Travel Time (ms) FILTERED REFLECTIVITY (Ormsby 8 -10 -40 -50 Hz) Frequency

Individual Amplitude Spectra • The temporal thickness of the wedge (t) determines the period

Discrete Frequency Components • The value of the frequency component (f) determines the period

The Tuning Cube y x z 3 -D Seismic Volume Interpret y x Interpreted

Prior to Spectral Balancing • The Tuning Cube contains three main components: – thin

Spectral Balancing Tuning Cube y x freq Split Spectral Tuning Cube into Discrete Frequencies

After Spectral Balancing • The Tuning Cube contains two main components: – thin bed

Real Data Example • Gulf-of-Mexico, Pleistocene-age equivalent of the modern-day Mississippi River Delta.

Response Amplitude Channel “A” Fault-Controlled Channel Point Bar Amplitude 1 0 N Channel “B”

Tuning Cube, Amplitude at Frequency = 16 hz Channel “A” North-South Extent of Channel

Tuning Cube, Amplitude at Frequency = 26 hz Channel “A” North-South Extent of Channel

Hey…what about the phase? • Amplitude spectra delineate thin bed variability via spectral notching.

Response Phase Faults Phase 180 -180 N Gulf of Mexico Example 10, 000 ft

Tuning Cube, Phase at Frequency = 16 hz Faults Phase 180 -180 N Gulf

Tuning Cube, Phase at Frequency = 26 hz Faults Phase 180 -180 N Gulf

Discrete Frequency Energy Cubes z y x 3 -D Seismic Volume z=1 z=n Compute

Summary • Spectral decomposition uses the discrete Fourier transform to quantify thin-bed interference and

Slides: 34

Download presentation

Interpretational Applications of Spectral Decomposition Greg Partyka, James Gridley, and John Lopez

Spectral Decomposition • uses the discrete Fourier transform to: – quantify thin-bed interference, and – detect subtle discontinuities.

Outline • • Convolutional Model Implications Wedge Model Response The Tuning Cube Spectral Balancing Real Data Examples Alternatives to the Tuning Cube Summary

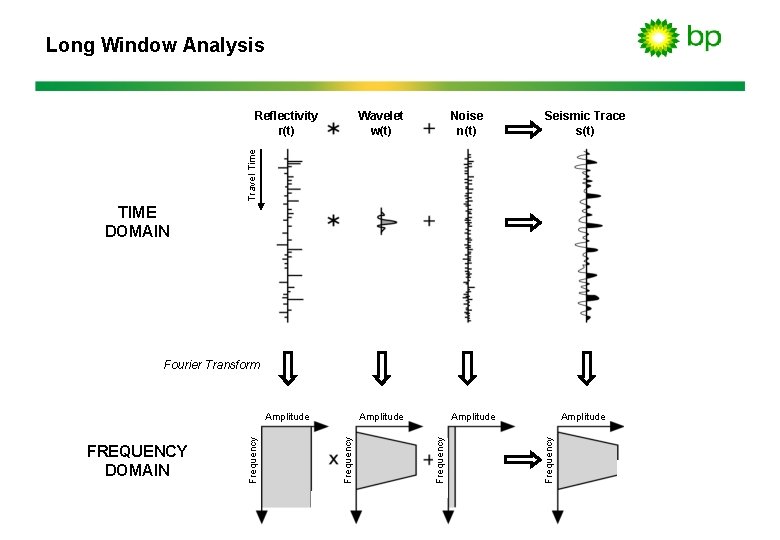
Long Window Analysis • The geology is unpredictable. • Its reflectivity spectrum is therefore white/blue.

Long Window Analysis Wavelet w(t) Noise n(t) Amplitude Seismic Trace s(t) Travel Time Reflectivity r(t) TIME DOMAIN Amplitude Frequency FREQUENCY DOMAIN Frequency Amplitude Frequency Fourier Transform

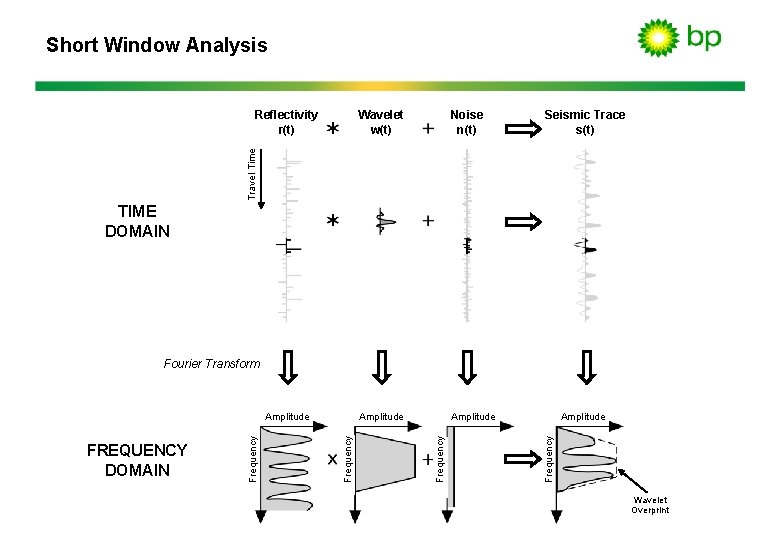
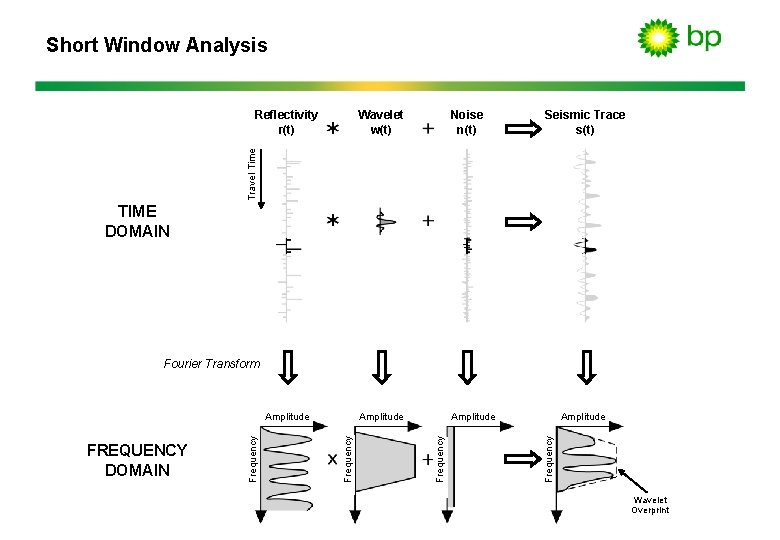
Short Window Analysis • The non-random geology locally filters the reflecting wavelet. • Its non-white reflectivity spectrum represents the interference pattern within the short analysis window.

Short Window Analysis Wavelet w(t) Noise n(t) Amplitude Seismic Trace s(t) Travel Time Reflectivity r(t) TIME DOMAIN Amplitude Frequency FREQUENCY DOMAIN Frequency Amplitude Frequency Fourier Transform Wavelet Overprint

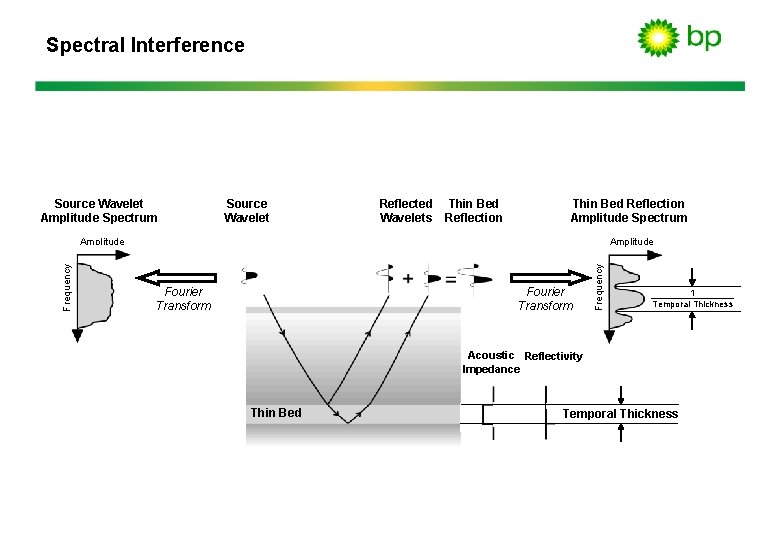
Spectral Interference • The spectral interference pattern is imposed by the distribution of acoustic properties within the short analysis window.

Spectral Interference Source Wavelet Amplitude Spectrum Source Wavelet Reflected Thin Bed Wavelets Reflection Thin Bed Reflection Amplitude Spectrum Amplitude Fourier Transform Frequency Amplitude 1 Temporal Thickness Acoustic Reflectivity Impedance Thin Bed Temporal Thickness

Outline • • Convolutional Model Implications Wedge Model Response The Tuning Cube Spectral Balancing Real Data Examples Alternatives to the Tuning Cube Summary

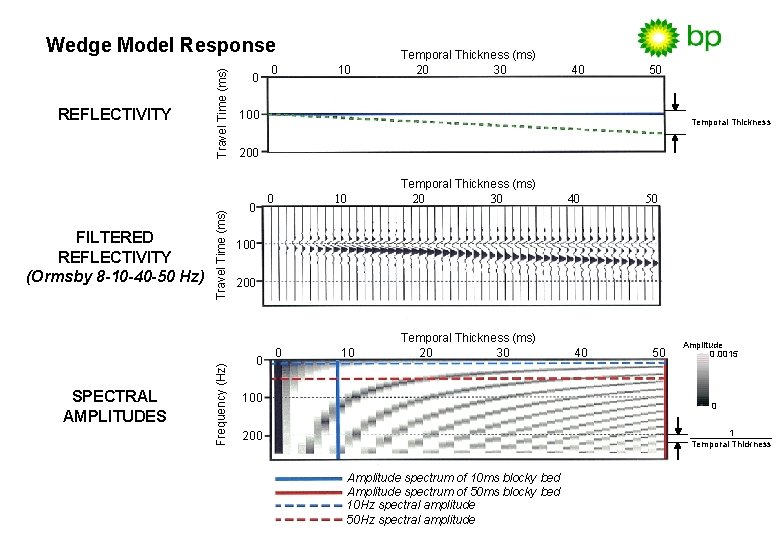
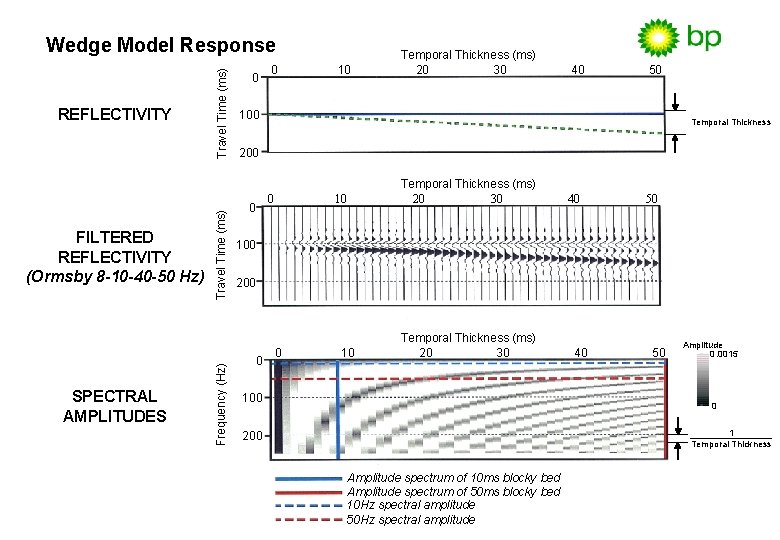
SPECTRAL AMPLITUDES Travel Time (ms) FILTERED REFLECTIVITY (Ormsby 8 -10 -40 -50 Hz) Frequency (Hz) REFLECTIVITY Travel Time (ms) Wedge Model Response 0 0 10 Temporal Thickness (ms) 20 30 40 50 100 Temporal Thickness 200 0 0 10 Temporal Thickness (ms) 20 30 40 50 100 200 0 0 10 Temporal Thickness (ms) 20 30 100 40 50 Amplitude 0. 0015 0 1 Temporal Thickness 200 Amplitude spectrum of 10 ms blocky bed Amplitude spectrum of 50 ms blocky bed 10 Hz spectral amplitude 50 Hz spectral amplitude

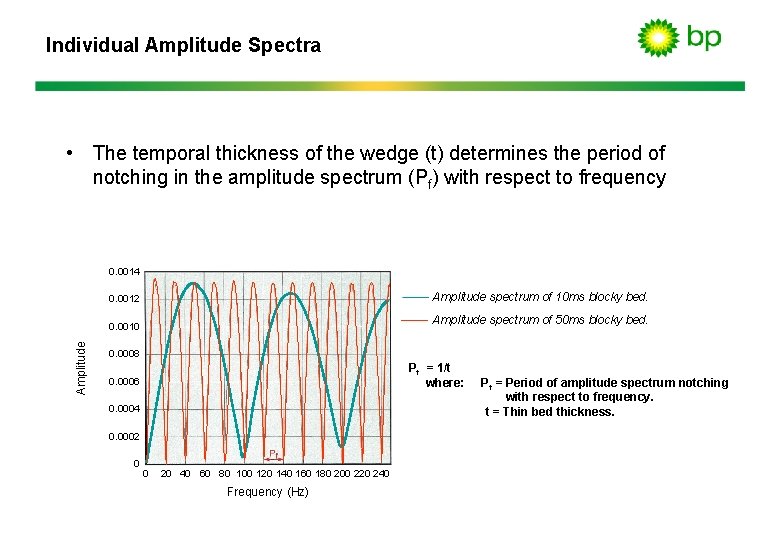
Individual Amplitude Spectra • The temporal thickness of the wedge (t) determines the period of notching in the amplitude spectrum (Pf) with respect to frequency 0. 0014 Amplitude spectrum of 10 ms blocky bed. 0. 0012 Amplitude spectrum of 50 ms blocky bed. Amplitude 0. 0010 0. 0008 Pf = 1/t where: 0. 0006 0. 0004 0. 0002 0 0 20 40 60 80 100 120 140 160 180 200 220 240 Frequency (Hz) P f = Period of amplitude spectrum notching with respect to frequency. t = Thin bed thickness.

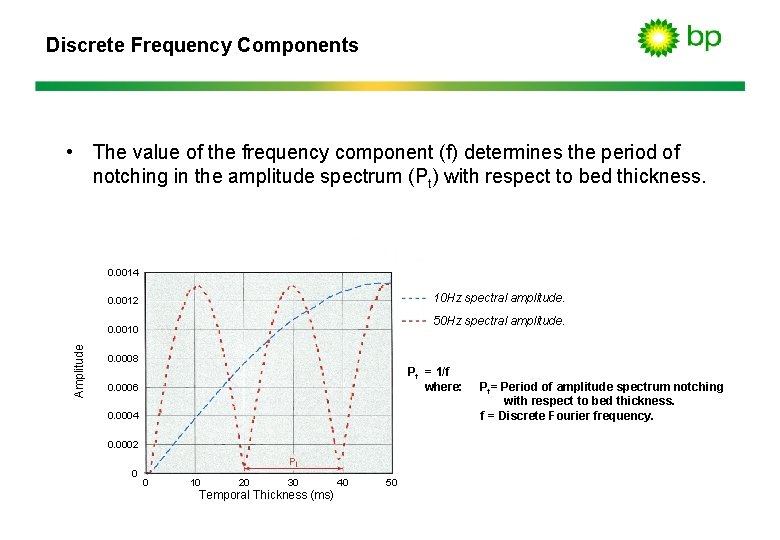
Discrete Frequency Components • The value of the frequency component (f) determines the period of notching in the amplitude spectrum (Pt) with respect to bed thickness. 0. 0014 10 Hz spectral amplitude. 0. 0012 50 Hz spectral amplitude. Amplitude 0. 0010 0. 0008 Pt = 1/f where: 0. 0006 0. 0004 0. 0002 0 0 10 20 30 Temporal Thickness (ms) 40 50 P t= Period of amplitude spectrum notching with respect to bed thickness. f = Discrete Fourier frequency.

Outline • • Convolutional Model Implications Wedge Model Response The Tuning Cube Spectral Balancing Real Data Examples Alternatives to the Tuning Cube Summary

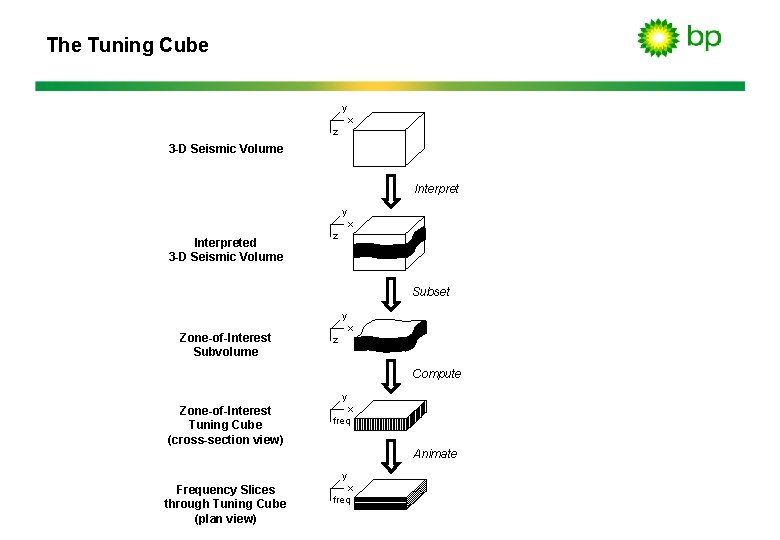
The Tuning Cube y x z 3 -D Seismic Volume Interpret y x Interpreted 3 -D Seismic Volume z Subset y Zone-of-Interest Subvolume x z Compute y Zone-of-Interest Tuning Cube (cross-section view) x freq Animate y Frequency Slices through Tuning Cube (plan view) x freq

Outline • • Convolutional Model Implications Wedge Model Response The Tuning Cube Spectral Balancing Real Data Examples Alternatives to the Tuning Cube Summary

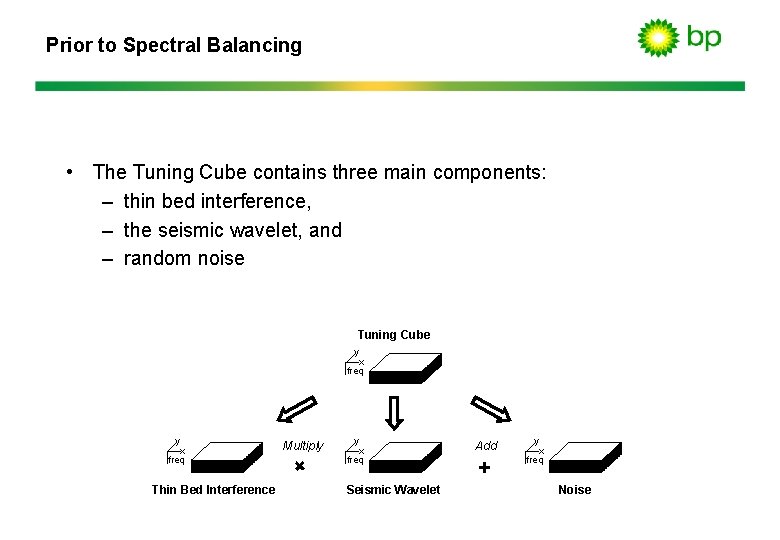
Prior to Spectral Balancing • The Tuning Cube contains three main components: – thin bed interference, – the seismic wavelet, and – random noise Tuning Cube y x freq Thin Bed Interference Multiply + y x freq Seismic Wavelet Add + y x freq Noise

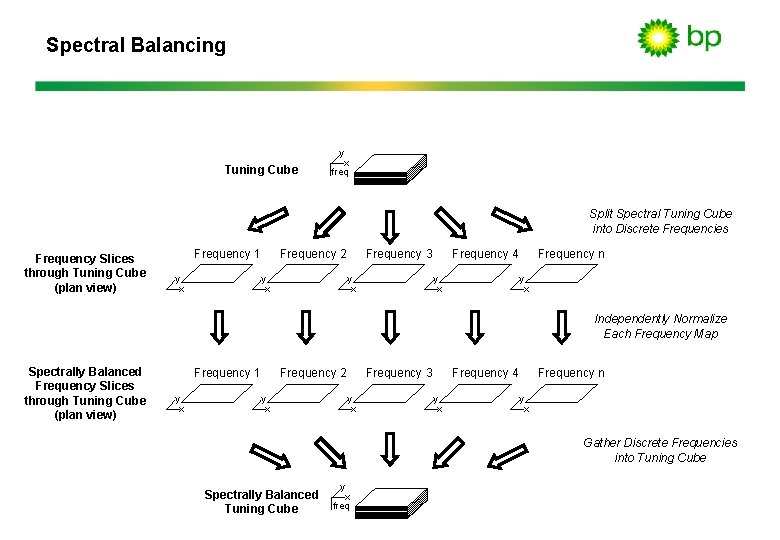
Spectral Balancing Tuning Cube y x freq Split Spectral Tuning Cube into Discrete Frequencies Frequency Slices through Tuning Cube (plan view) Frequency 1 y x Frequency 2 y x Frequency 3 y x Frequency 4 y x Frequency n y x Independently Normalize Each Frequency Map Spectrally Balanced Frequency Slices through Tuning Cube (plan view) Frequency 1 y x Frequency 2 y x Frequency 3 y x Frequency 4 y x Frequency n y x Gather Discrete Frequencies into Tuning Cube Spectrally Balanced Tuning Cube y x freq

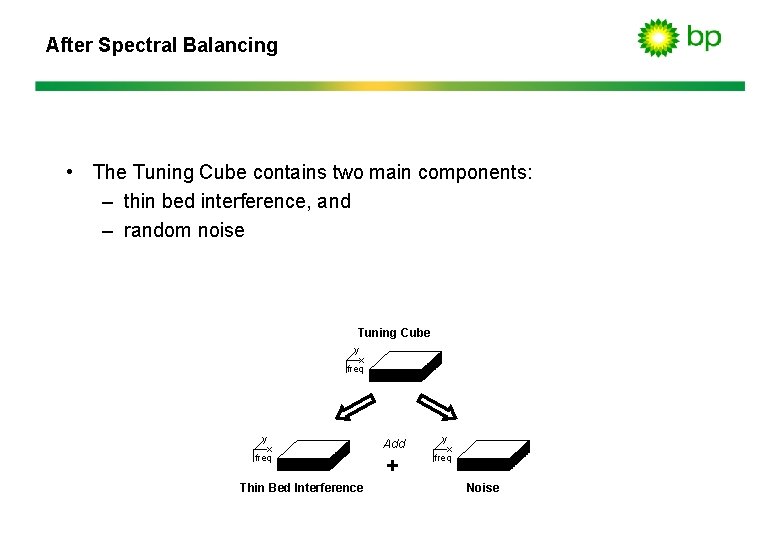
After Spectral Balancing • The Tuning Cube contains two main components: – thin bed interference, and – random noise Tuning Cube y x freq Thin Bed Interference Add + y x freq Noise

Outline • • Convolutional Model Implications Wedge Model Response The Tuning Cube Spectral Balancing Real Data Examples Alternatives to the Tuning Cube Summary

Real Data Example • Gulf-of-Mexico, Pleistocene-age equivalent of the modern-day Mississippi River Delta.

Response Amplitude Channel “A” Fault-Controlled Channel Point Bar Amplitude 1 0 N Channel “B” Gulf of Mexico Example 10, 000 ft analysis window length = 100 ms

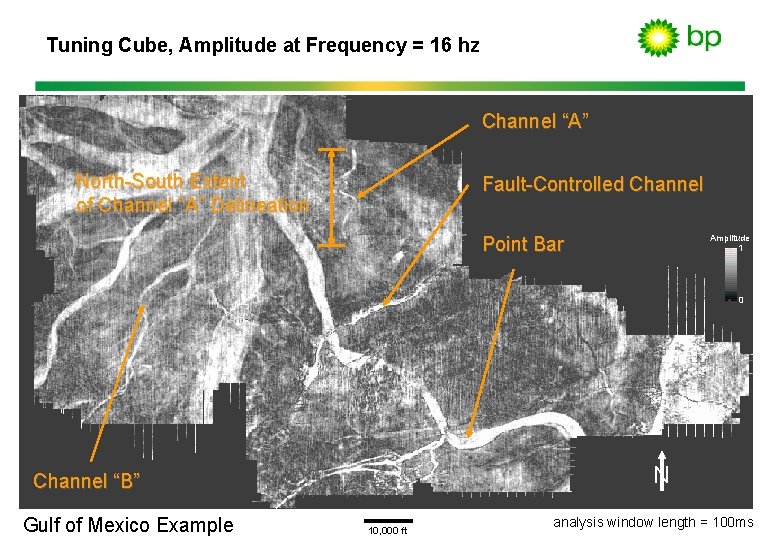
Tuning Cube, Amplitude at Frequency = 16 hz Channel “A” North-South Extent of Channel “A” Delineation Fault-Controlled Channel Point Bar Amplitude 1 0 N Channel “B” Gulf of Mexico Example 10, 000 ft analysis window length = 100 ms

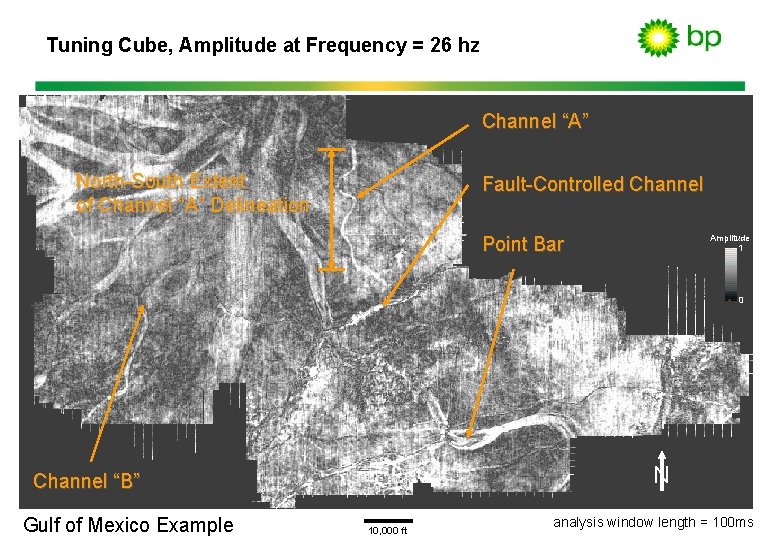
Tuning Cube, Amplitude at Frequency = 26 hz Channel “A” North-South Extent of Channel “A” Delineation Fault-Controlled Channel Point Bar Amplitude 1 0 N Channel “B” Gulf of Mexico Example 10, 000 ft analysis window length = 100 ms

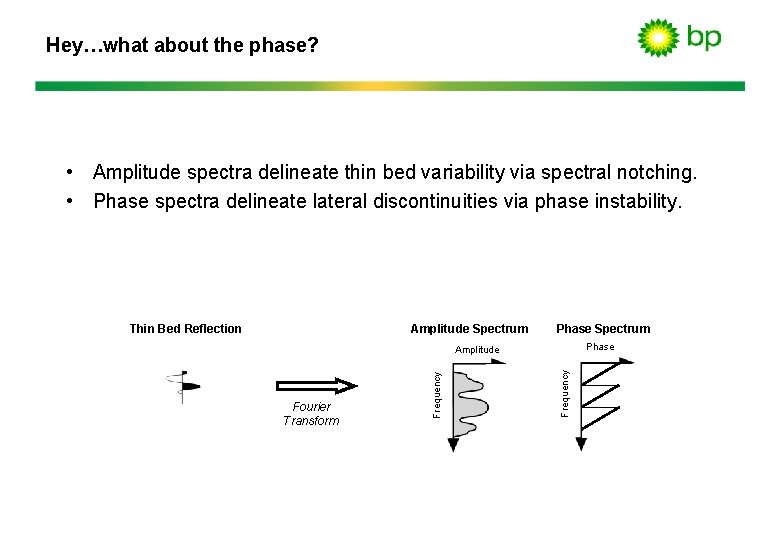
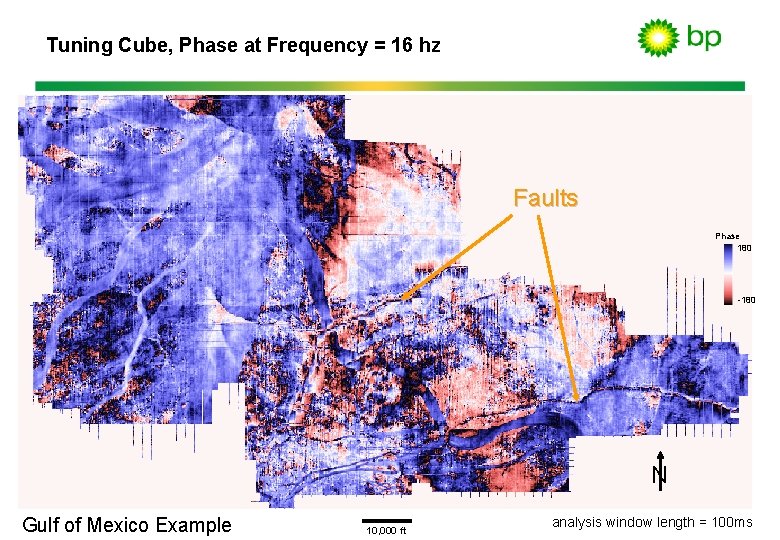
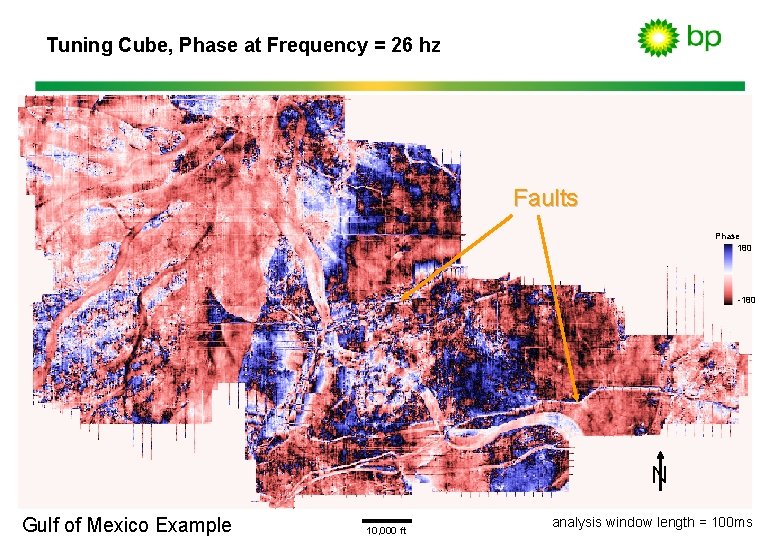
Hey…what about the phase? • Amplitude spectra delineate thin bed variability via spectral notching. • Phase spectra delineate lateral discontinuities via phase instability. Amplitude Spectrum Thin Bed Reflection Phase Spectrum Phase Frequency Fourier Transform Frequency Amplitude

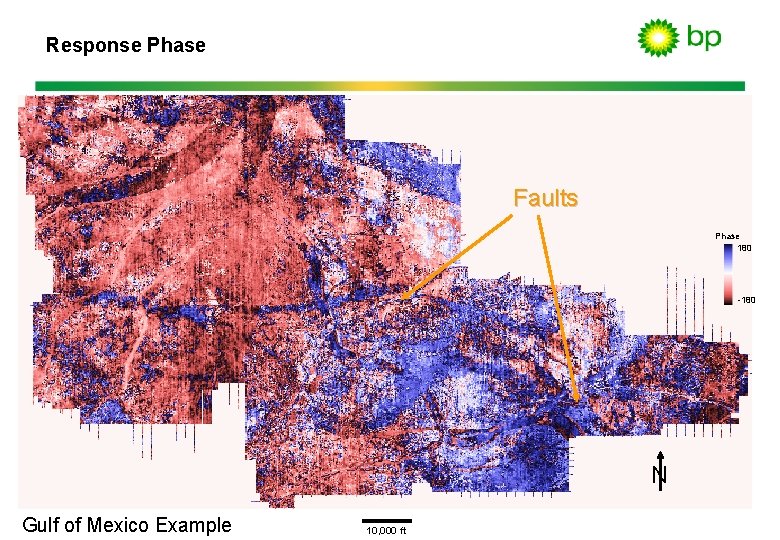
Response Phase Faults Phase 180 -180 N Gulf of Mexico Example 10, 000 ft

Tuning Cube, Phase at Frequency = 16 hz Faults Phase 180 -180 N Gulf of Mexico Example 10, 000 ft analysis window length = 100 ms

Tuning Cube, Phase at Frequency = 26 hz Faults Phase 180 -180 N Gulf of Mexico Example 10, 000 ft analysis window length = 100 ms

Outline • • Convolutional Model Implications Wedge Model Response The Tuning Cube Spectral Balancing Real Data Examples Alternatives to the Tuning Cube Summary

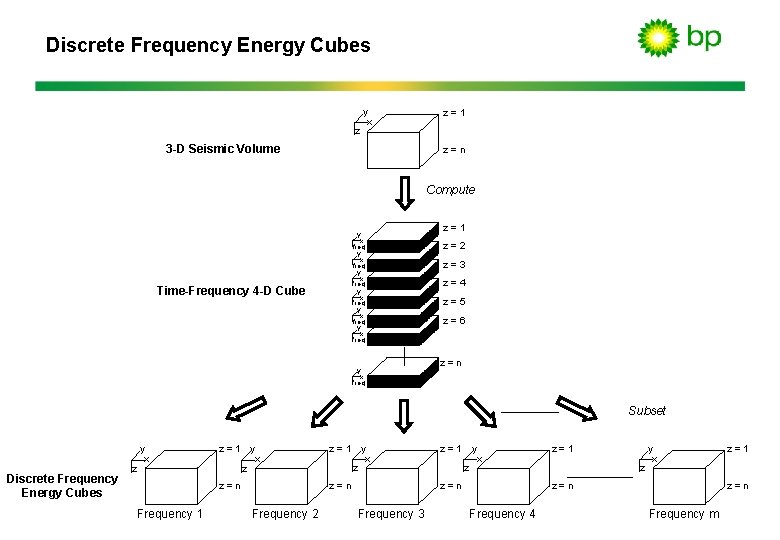
Discrete Frequency Energy Cubes z y x 3 -D Seismic Volume z=1 z=n Compute y x freq y x freq Time-Frequency 4 -D Cube y x freq z=1 z=2 z=3 z=4 z=5 z=6 z=n Subset Discrete Frequency Energy Cubes z y x Frequency 1 z=1 y x z z=1 z=n z=n Frequency 2 Frequency 3 z y x z=1 z y x z=n Frequency 4 z=1 z=n Frequency m

Outline • • Convolutional Model Implications Wedge Model Response The Tuning Cube Spectral Balancing Real Data Examples Alternatives to the Tuning Cube Summary

Summary • Spectral decomposition uses the discrete Fourier transform to quantify thin-bed interference and detect subtle discontinuities. • For reservoir characterization, our most common approach to viewing and analyzing spectral decompositions is via the “Zone-of-Interest Tuning Cube”. • Spectral balancing removes the wavelet overprint. • The amplitude component excels at quantifying thickness variability and detecting lateral discontinuities. • The phase component detects lateral discontinuities.