Interpolation and Polynomial Approximation Problem Let x 0

Interpolation and Polynomial Approximation • Problem: Let x 0, x 1, …xn be (n+1) distinct points on the real axis. We wish to construct a polynomial P(x) of degree <= n. that is satisfies P(xk) = wk for k= 0, 1, 2, …n. Dr. Ghaddar mghaddar@ul. edu. lb 1

• Existence and uniqueness of solution Let P(x) = a 0. xn + a 1. xn-1 +…+an-1. x + an • Linear system (n+1) equations in (n+1) unknown: Dr. Ghaddar mghaddar@ul. edu. lb 2

• The linear system has a solution if : • The determinant is called determinant Van der Monde. Dr. Ghaddar mghaddar@ul. edu. lb 3

Verify Dr. Ghaddar mghaddar@ul. edu. lb 4

• Lagrange Formula: The polynomial P(x) of degree at most n that passes through the (n+1) points (x 0, w 0), (x 1, w 1), …(xn, wn) and has the form: Dr. Ghaddar mghaddar@ul. edu. lb 5

• Example: P(-1) = 3 ; P(1) =1 ; P(2) = 3 et P(3) = 7 Dr. Ghaddar mghaddar@ul. edu. lb 6

• Newton Interpolation Polynomial Dr. Ghaddar mghaddar@ul. edu. lb 7

• The Divided Difference table: Dr. Ghaddar mghaddar@ul. edu. lb 8

• Example: p(1) = 2, P(3)=-1, P(4)=5, P(5) =1 Dr. Ghaddar mghaddar@ul. edu. lb 9

Dr. Ghaddar mghaddar@ul. edu. lb 10

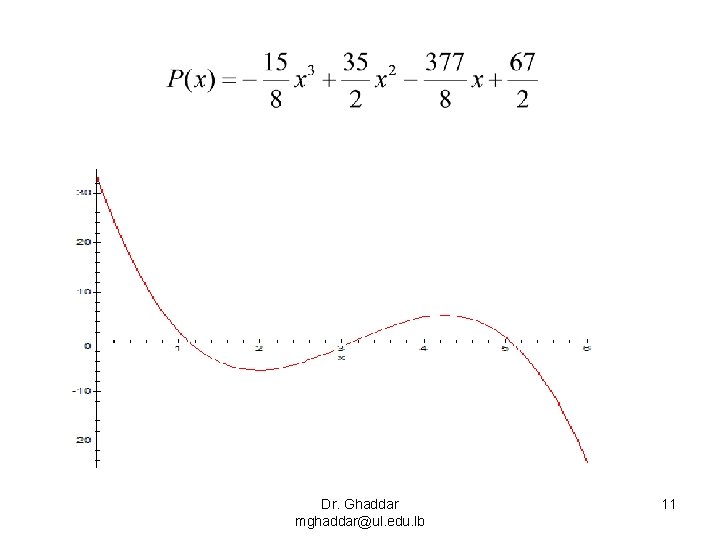
Dr. Ghaddar mghaddar@ul. edu. lb 11

Algorithm for interpolation with a Lagrangian polynomial • To interpolate for f(x), given x and a set of N+1 data pairs, (xi, fi), I = 0, …, N: • Set SUM = 0. DO For I = 0 to N: SET P = 1. DO FOR J = 0 to N: IF J ≠ I: SET P = P*(x - x(J) )/ (x(I) - x(J)). ENDO (J). SET SUM = SUM + P*fi ENDO (I). SUM is the interpolated value. Dr. Ghaddar mghaddar@ul. edu. lb 12

The Error of the interpolating polynomial • Let x 0, x 1, . . , xn be (n+1) distinct points on the real axis and let f(x) be a real-valued function defined on some interval [a, b] containing these points, we wish to construct P(x) of degree <= n which interpolates f(x) at the points x 0, x 1, . . , xn that is satisfies • R(x) is the interpolation error R(x) = 0 if x = xk k=0, 1, …, n Dr. Ghaddar mghaddar@ul. edu. lb 13

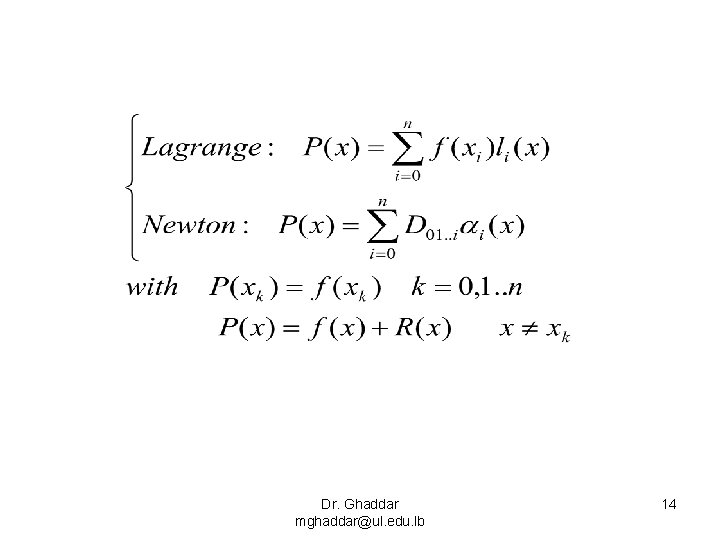
Dr. Ghaddar mghaddar@ul. edu. lb 14

Interpolation Error • • • f(x) = 1/x, x 0 = 2, x 1 = 2. 5, x 2 = 4 f(2) = 0. 5, f(2. 5) = 0. 4, f(4) = 0. 25 P(x) = 0. 05 x 2 - 0. 425 x + 1. 15 P(3) = 0. 325 f(3) = 0. 333 |R(3)|= 0. 008 Dr. Ghaddar mghaddar@ul. edu. lb 15

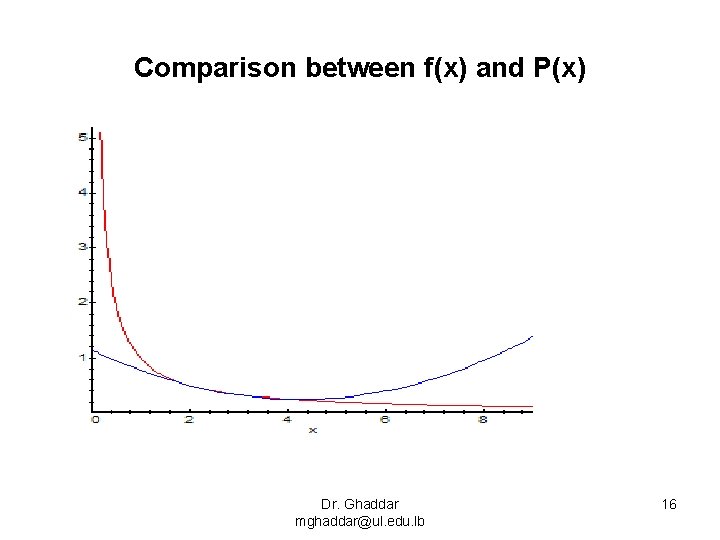
Comparison between f(x) and P(x) Dr. Ghaddar mghaddar@ul. edu. lb 16

The Error of the interpolating polynomial • Cauchy Th. : Let f(x) be a real-valued function defined on [a, b] and (n+1) times differentiable on [a, b]. If P(x) is the polynomial of degree <= n which interpolates f(x) at the (n+1) distinct points x 0, x 1, . . , xn, in [a, b], there exists t between [a, b] such that: Dr. Ghaddar mghaddar@ul. edu. lb 17

Interpolation in a function based on equally spaced points • Note : xk = x 0 + k. h and x = x 0 +s. h K= 0, 1, …, n s : variable Dr. Ghaddar mghaddar@ul. edu. lb h: step 18

Lagrange Formula Dr. Ghaddar mghaddar@ul. edu. lb 19

Newton Formula Dr. Ghaddar mghaddar@ul. edu. lb 20