INTERPOLASI 1 Direct Method of Interpolation What is

INTERPOLASI 1

Direct Method of Interpolation

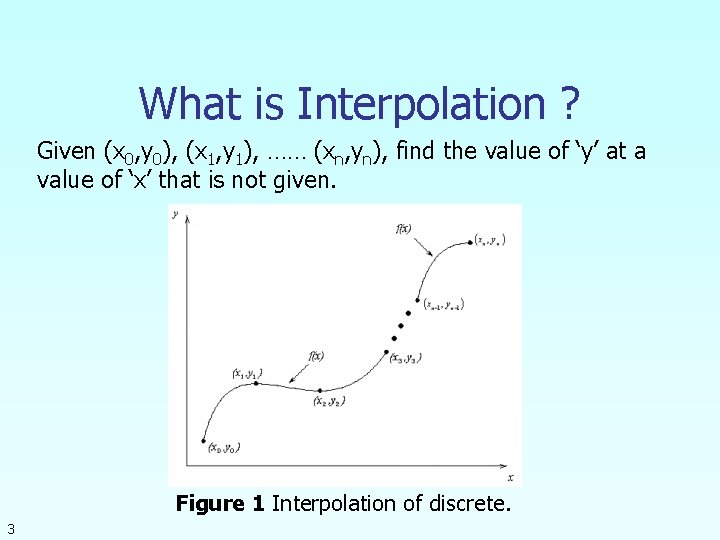
What is Interpolation ? Given (x 0, y 0), (x 1, y 1), …… (xn, yn), find the value of ‘y’ at a value of ‘x’ that is not given. Figure 1 Interpolation of discrete. 3

Interpolants Polynomials are the most common choice of interpolants because they are easy to: Evaluate Differentiate, and Integrate 4

Direct Method Given ‘n+1’ data points (x 0, y 0), (x 1, y 1), …………. . (xn, yn), pass a polynomial of order ‘n’ through the data as given below: where a 0, a 1, ………………. an are real constants. n Set up ‘n+1’ equations to find ‘n+1’ constants. n To find the value ‘y’ at a given value of ‘x’, simply substitute the value of ‘x’ in the above polynomial. 5

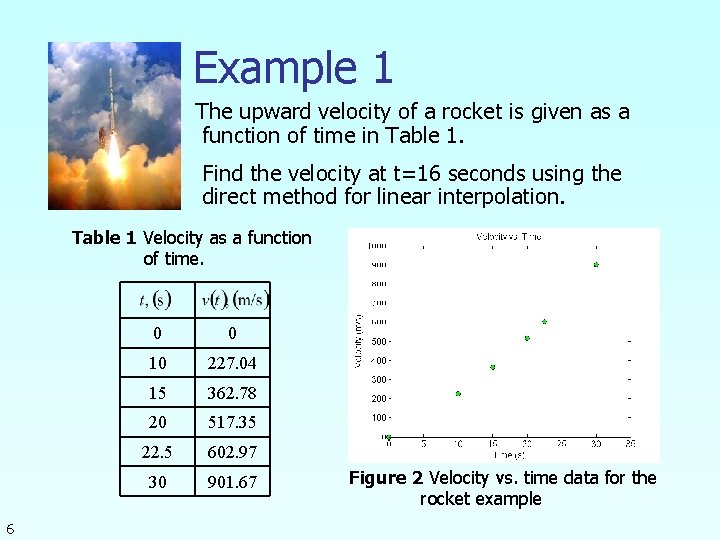
Example 1 The upward velocity of a rocket is given as a function of time in Table 1. Find the velocity at t=16 seconds using the direct method for linear interpolation. Table 1 Velocity as a function of time. 6 0 0 10 227. 04 15 362. 78 20 517. 35 22. 5 602. 97 30 901. 67 Figure 2 Velocity vs. time data for the rocket example

Linear Interpolation Solving the above two equations gives, Figure 3 Linear interpolation. Hence 7

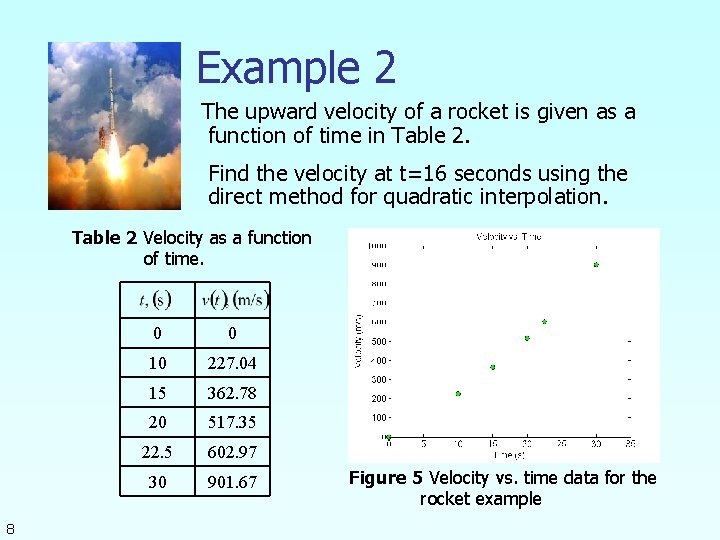
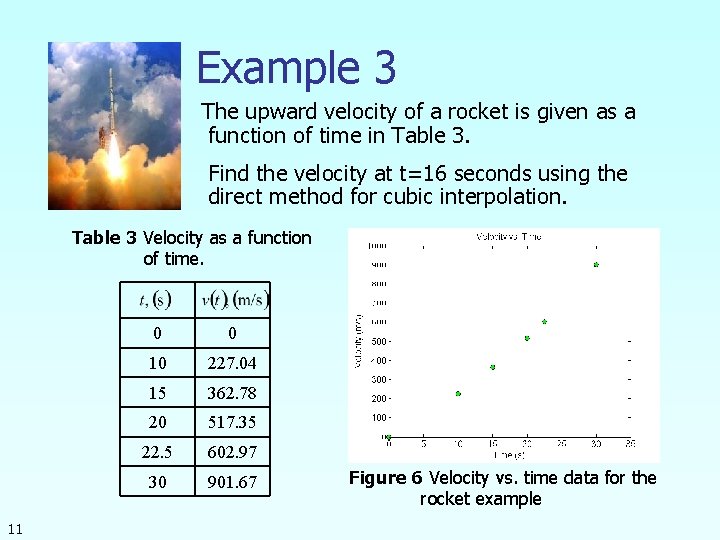
Example 2 The upward velocity of a rocket is given as a function of time in Table 2. Find the velocity at t=16 seconds using the direct method for quadratic interpolation. Table 2 Velocity as a function of time. 8 0 0 10 227. 04 15 362. 78 20 517. 35 22. 5 602. 97 30 901. 67 Figure 5 Velocity vs. time data for the rocket example

Quadratic Interpolation Figure 6 Quadratic interpolation. Solving the above three equations gives 9

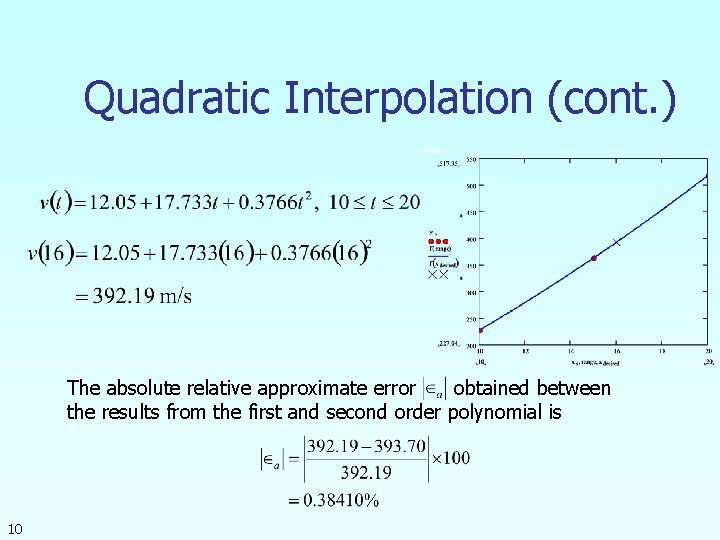
Quadratic Interpolation (cont. ) The absolute relative approximate error obtained between the results from the first and second order polynomial is 10

Example 3 The upward velocity of a rocket is given as a function of time in Table 3. Find the velocity at t=16 seconds using the direct method for cubic interpolation. Table 3 Velocity as a function of time. 11 0 0 10 227. 04 15 362. 78 20 517. 35 22. 5 602. 97 30 901. 67 Figure 6 Velocity vs. time data for the rocket example

Cubic Interpolation Figure 7 Cubic interpolation. 12

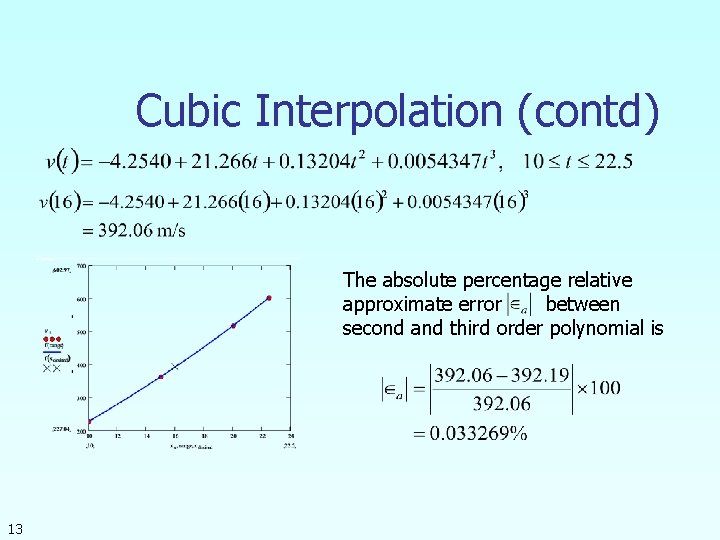
Cubic Interpolation (contd) The absolute percentage relative approximate error between second and third order polynomial is 13

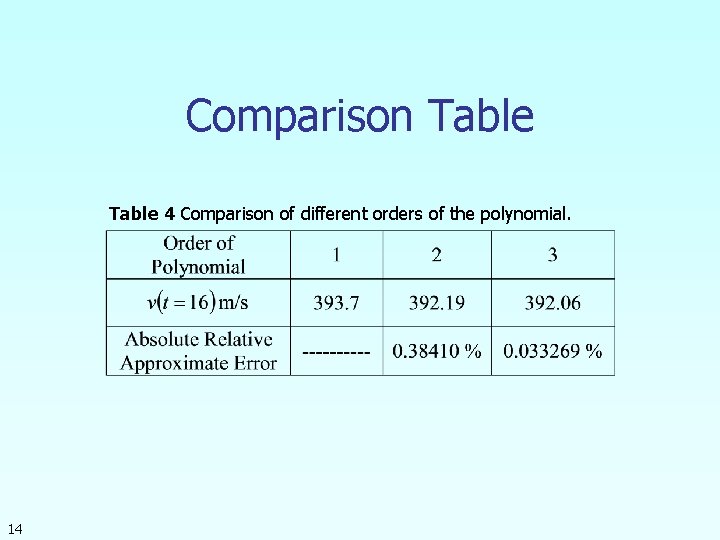
Comparison Table 4 Comparison of different orders of the polynomial. 14

Distance from Velocity Profile Find the distance covered by the rocket from t=11 s to t=16 s ? 15

Acceleration from Velocity Profile Find the acceleration of the rocket at t=16 s given that 16

Lagrange Method of Interpolation

What is Interpolation ? Given (x 0, y 0), (x 1, y 1), …… (xn, yn), find the value of ‘y’ at a value of ‘x’ that is not given. 18

Interpolants Polynomials are the most common choice of interpolants because they are easy to: Evaluate Differentiate, and Integrate. 19

Lagrangian Interpolation 20

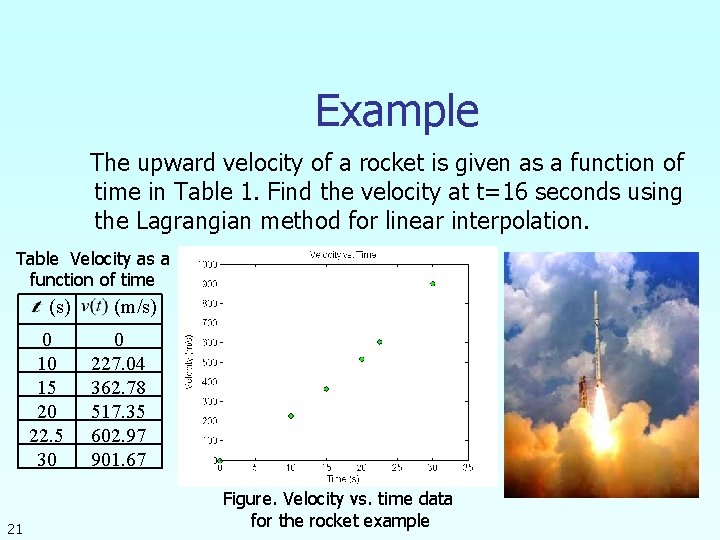
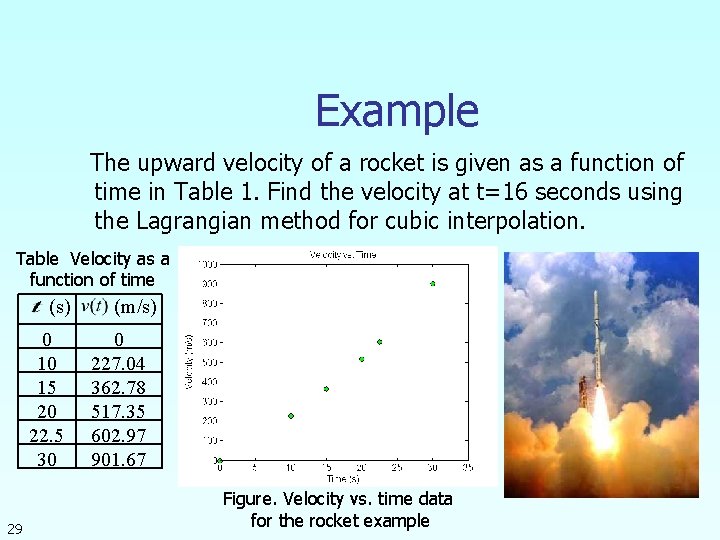
Example The upward velocity of a rocket is given as a function of time in Table 1. Find the velocity at t=16 seconds using the Lagrangian method for linear interpolation. Table Velocity as a function of time (s) 0 10 15 20 22. 5 30 21 (m/s) 0 227. 04 362. 78 517. 35 602. 97 901. 67 Figure. Velocity vs. time data for the rocket example

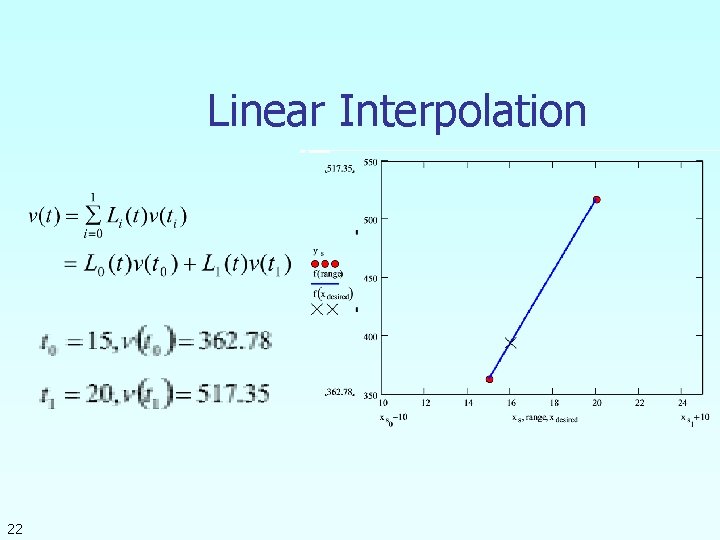
Linear Interpolation 22

Linear Interpolation (contd) 23

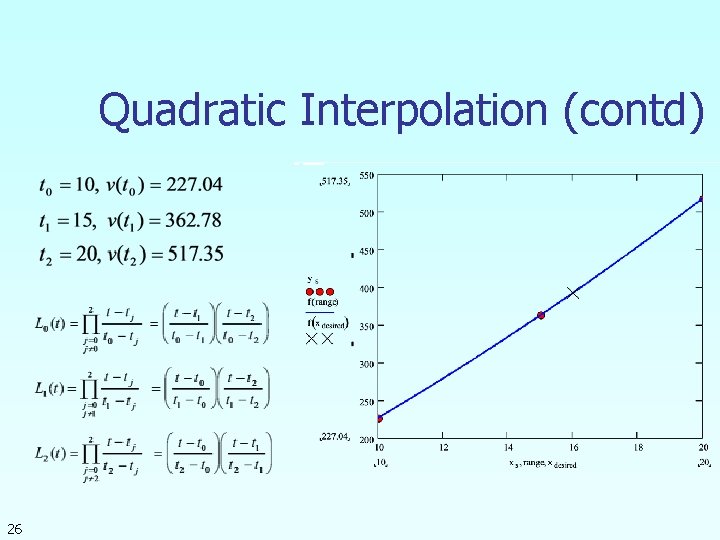
Quadratic Interpolation 24

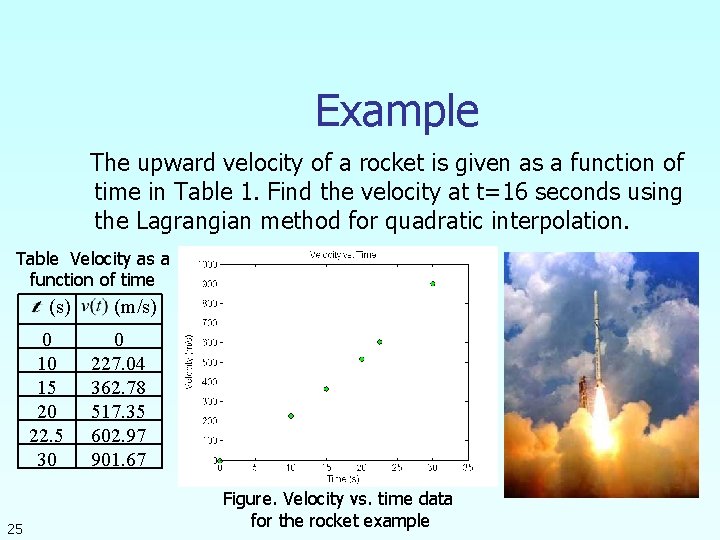
Example The upward velocity of a rocket is given as a function of time in Table 1. Find the velocity at t=16 seconds using the Lagrangian method for quadratic interpolation. Table Velocity as a function of time (s) 0 10 15 20 22. 5 30 25 (m/s) 0 227. 04 362. 78 517. 35 602. 97 901. 67 Figure. Velocity vs. time data for the rocket example

Quadratic Interpolation (contd) 26

Quadratic Interpolation (contd) The absolute relative approximate error obtained between the results from the first and second order polynomial is 27

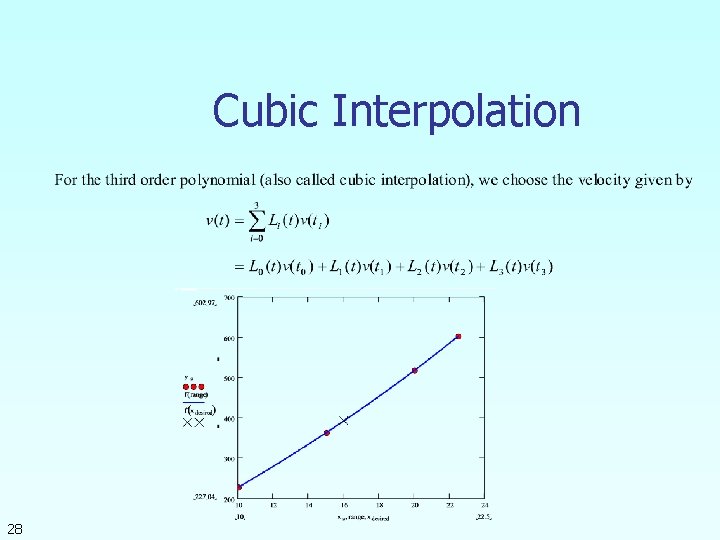
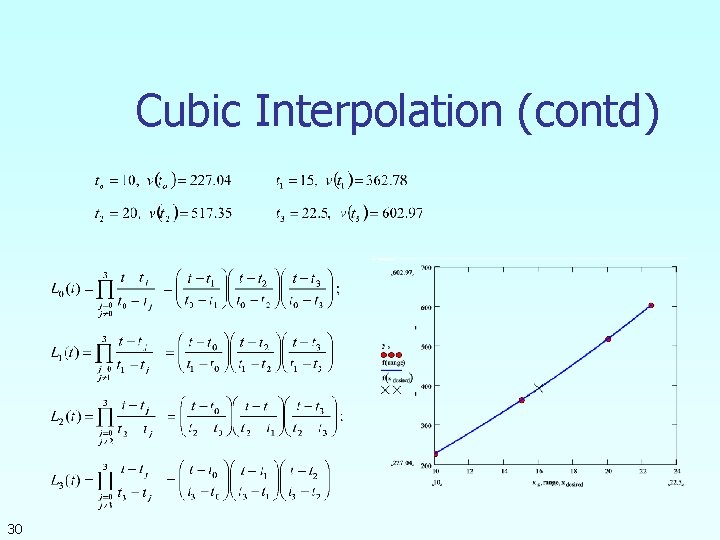
Cubic Interpolation 28

Example The upward velocity of a rocket is given as a function of time in Table 1. Find the velocity at t=16 seconds using the Lagrangian method for cubic interpolation. Table Velocity as a function of time (s) 0 10 15 20 22. 5 30 29 (m/s) 0 227. 04 362. 78 517. 35 602. 97 901. 67 Figure. Velocity vs. time data for the rocket example

Cubic Interpolation (contd) 30

Cubic Interpolation (contd) The absolute relative approximate error obtained between the results from the first and second order polynomial is 31

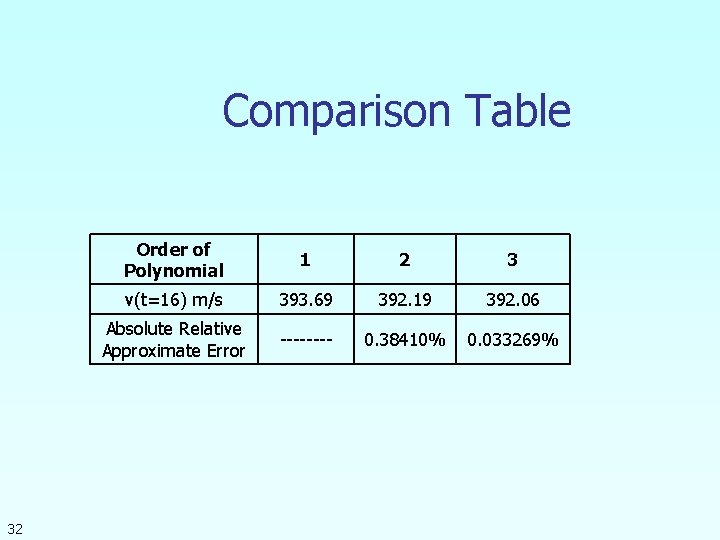
Comparison Table 32 Order of Polynomial 1 2 3 v(t=16) m/s 393. 69 392. 19 392. 06 Absolute Relative Approximate Error ---- 0. 38410% 0. 033269%

Distance from Velocity Profile Find the distance covered by the rocket from t=11 s to t=16 s ? 33

Acceleration from Velocity Profile Find the acceleration of the rocket at t=16 s given that , 34

Newton’s Divided Difference Method of Interpolation

What is Interpolation ? Given (x 0, y 0), (x 1, y 1), …… (xn, yn), find the value of ‘y’ at a value of ‘x’ that is not given. 36

Interpolants Polynomials are the most common choice of interpolants because they are easy to: Evaluate Differentiate, and Integrate. 37

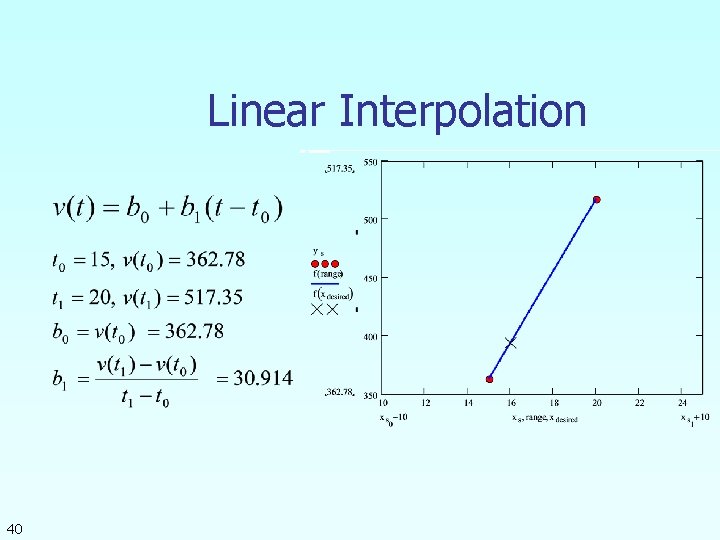
Newton’s Divided Difference Method Linear interpolation: Given linear interpolant through the data where 38 pass a

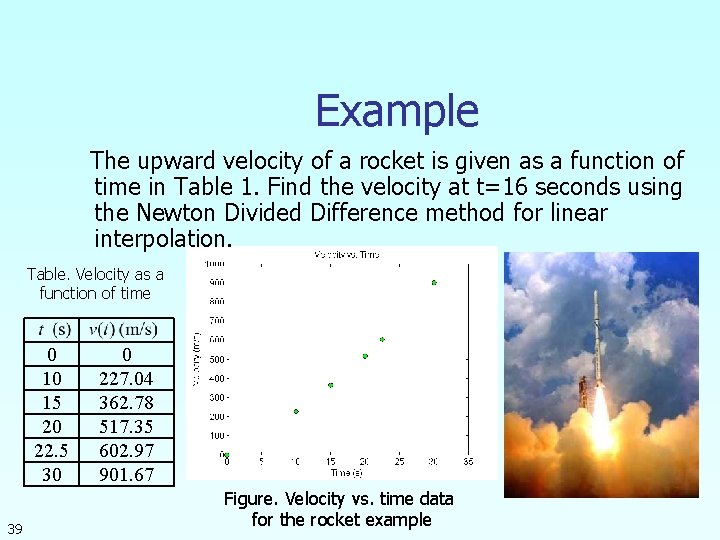
Example The upward velocity of a rocket is given as a function of time in Table 1. Find the velocity at t=16 seconds using the Newton Divided Difference method for linear interpolation. Table. Velocity as a function of time 0 10 15 20 22. 5 30 39 0 227. 04 362. 78 517. 35 602. 97 901. 67 Figure. Velocity vs. time data for the rocket example

Linear Interpolation 40

Linear Interpolation (contd) 41

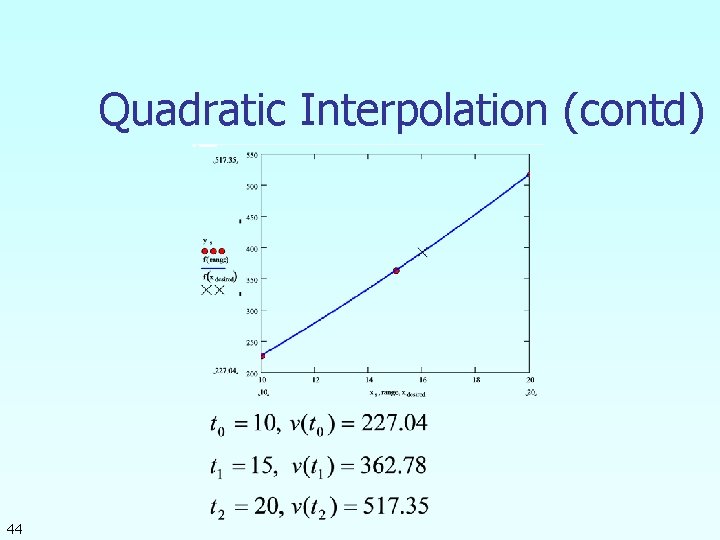
Quadratic Interpolation 42

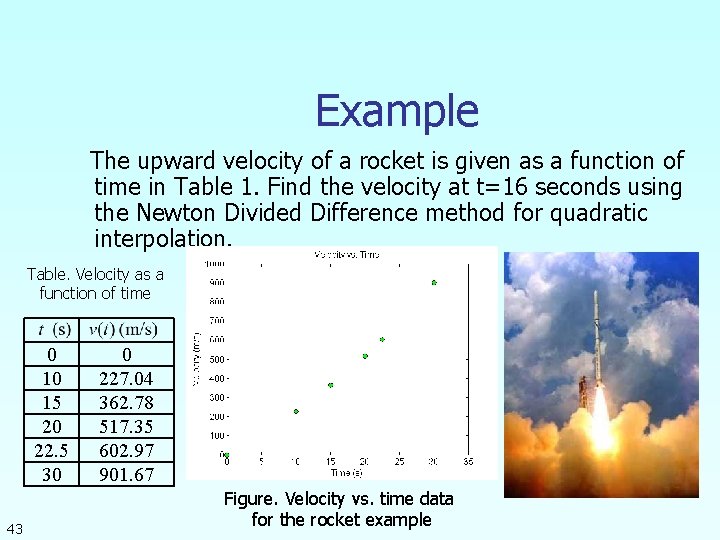
Example The upward velocity of a rocket is given as a function of time in Table 1. Find the velocity at t=16 seconds using the Newton Divided Difference method for quadratic interpolation. Table. Velocity as a function of time 0 10 15 20 22. 5 30 43 0 227. 04 362. 78 517. 35 602. 97 901. 67 Figure. Velocity vs. time data for the rocket example

Quadratic Interpolation (contd) 44

Quadratic Interpolation (contd) 45

Quadratic Interpolation (contd) 46

General Form where Rewriting 47

General Form 48

General form 49

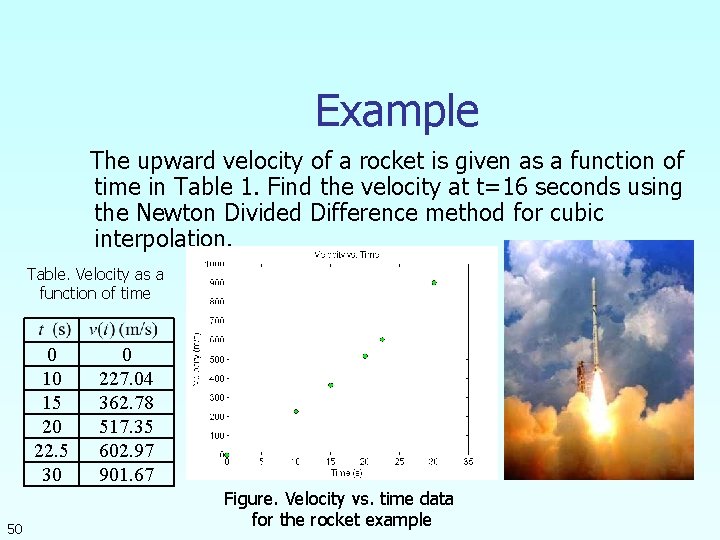
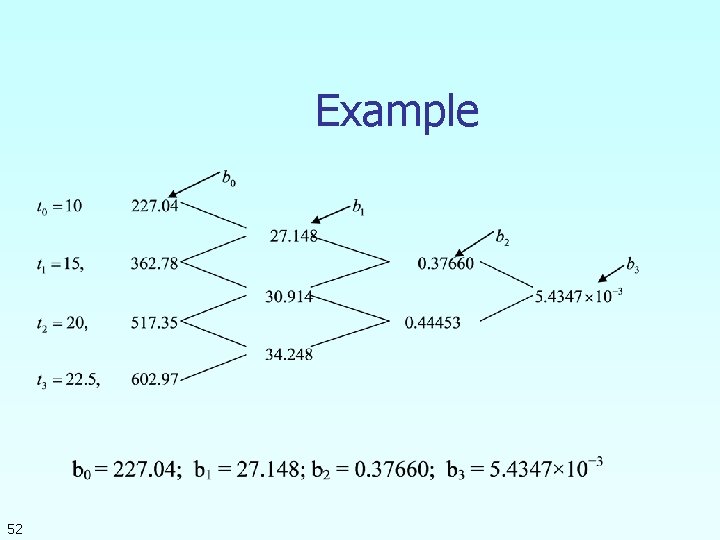
Example The upward velocity of a rocket is given as a function of time in Table 1. Find the velocity at t=16 seconds using the Newton Divided Difference method for cubic interpolation. Table. Velocity as a function of time 0 10 15 20 22. 5 30 50 0 227. 04 362. 78 517. 35 602. 97 901. 67 Figure. Velocity vs. time data for the rocket example

Example The velocity profile is chosen as we need to choose four data points that are closest to 51

Example 52

Example 53

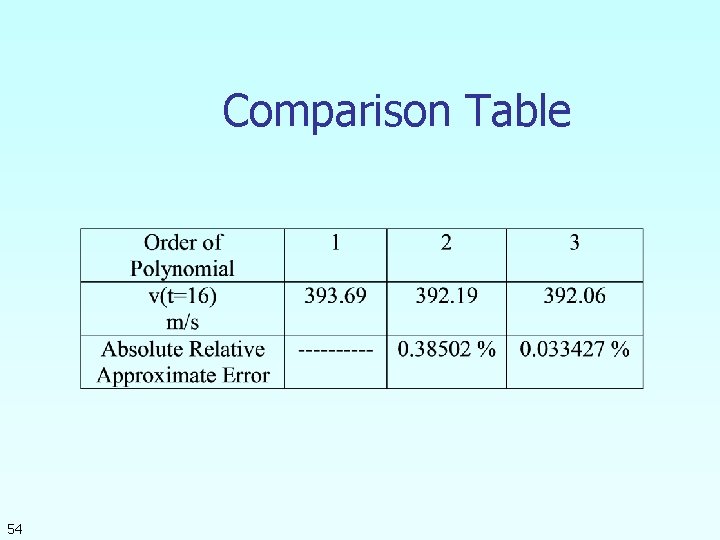
Comparison Table 54

Distance from Velocity Profile Find the distance covered by the rocket from t=11 s to t=16 s ? 55

Acceleration from Velocity Profile Find the acceleration of the rocket at t=16 s given that 56