Interpolacin y aproximacin polinomial Programacin Numrica Definicin Un

Interpolación y aproximación polinomial Programación Numérica

Definición Un polinomio de grado n es una expresión de la forma: P(x) = anxn + an-1 xn-1 +. . . +a 1 x + a 0 Donde an <> 0 Teorema (teorema de aproximación de Weierstrass) Suponga que f está definida y es continua en [a, b]. Para e > 0 existe un polinomio P definido en [a, b], con la propiedad de que |f(x) – P(x)| < e, para toda x en [a, b]

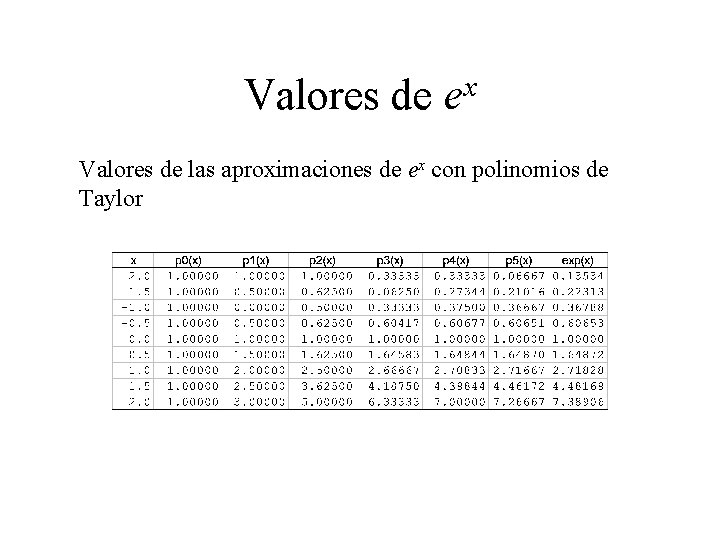
Desarrollo en series de Taylor Sea f(x) = ex Desarrollando en serie de Taylor alrededor de x = 0 P 0(x) = 1 P 1(x) = 1 + x P 3(x) = 1 + x 2/2 + x 3/6 P 2(x) = 1 + x 2/2 P 4(x) = 1 + x 2/2 + x 3/6 + x 4/24 P 5(x) = 1 + x 2/2 + x 3/6 + x 4/24 + x 5/120

Valores de x e Valores de las aproximaciones de ex con polinomios de Taylor

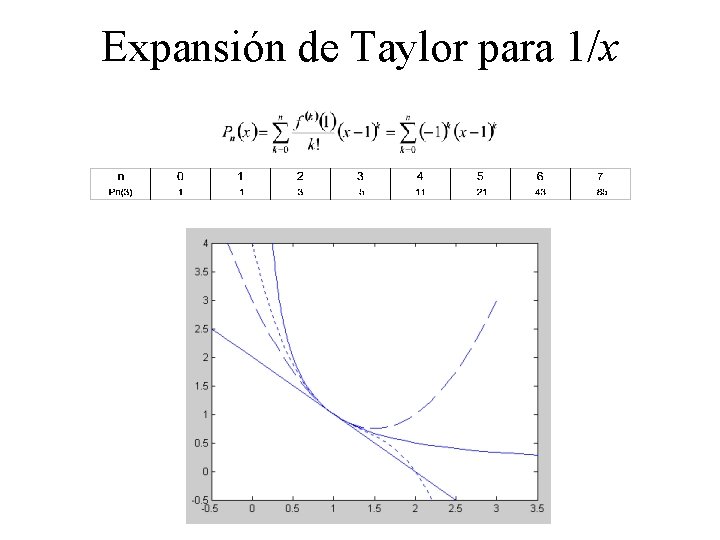
Expansión de Taylor para 1/x

Interpolación polinomial de Newton Revisaremos solo algunos casos: lineal, de segundo grado y de tercer grado.

Interpolación lineal Utilizando triángulos semejantes f(x) Reordenando f(x 1) f 1(x) f(x 0) x 0 x x 1

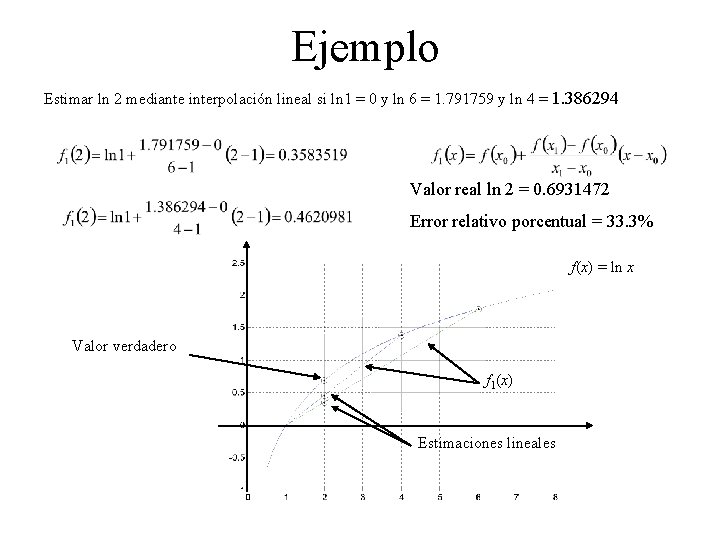
Ejemplo Estimar ln 2 mediante interpolación lineal si ln 1 = 0 y ln 6 = 1. 791759 y ln 4 = 1. 386294 Valor real ln 2 = 0. 6931472 Error relativo porcentual = 33. 3% f(x) = ln x Valor verdadero f 1(x) Estimaciones lineales

Interpolación cuadrática Polinomio cuadrático f 2(x) = b 0 + b 1(x – x 0) + b 2(x – x 0)(x – x 1) (1) simplificado f 2(x) = b 0 + b 1 x – b 1 x 0 + b 2 x 2 + b 2 x 0 x 1 – b 2 xx 0 – b 2 xx 1 Podemos escribirlo como f 2(x) = a 0 + a 1 x + a 2 x 2 Donde a 0 = b 0 – b 1 x 0 + b 2 x 0 x 1, a 1 = b 1 – b 2 x 0 – b 2 x 1, a 2=b 2 Podemos evaluar b 0, b 1 y b 2 sustituyendo x 0, x 1 y x 2 en la ecuación (1), se obtiene b 0 = f(x 0)

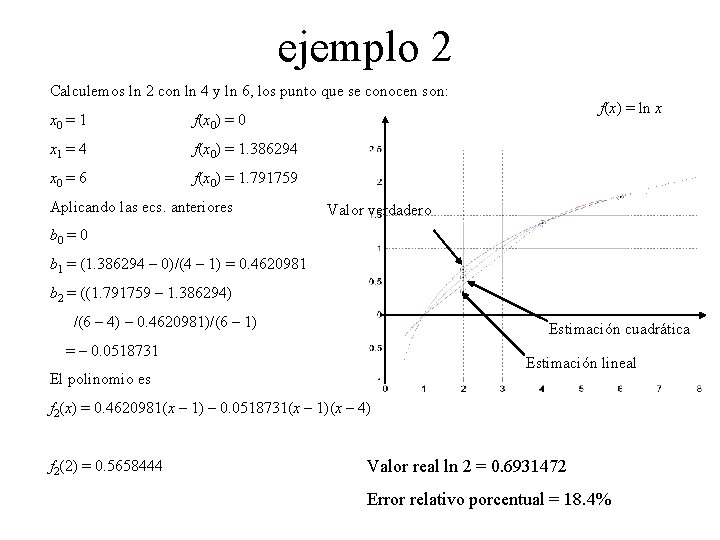
ejemplo 2 Calculemos ln 2 con ln 4 y ln 6, los punto que se conocen son: x 0 = 1 f(x 0) = 0 x 1 = 4 f(x 0) = 1. 386294 x 0 = 6 f(x 0) = 1. 791759 Aplicando las ecs. anteriores f(x) = ln x Valor verdadero b 0 = 0 b 1 = (1. 386294 – 0)/(4 – 1) = 0. 4620981 b 2 = ((1. 791759 – 1. 386294) /(6 – 4) – 0. 4620981)/(6 – 1) Estimación cuadrática = – 0. 0518731 Estimación lineal El polinomio es f 2(x) = 0. 4620981(x – 1) – 0. 0518731(x – 1)(x – 4) f 2(2) = 0. 5658444 Valor real ln 2 = 0. 6931472 Error relativo porcentual = 18. 4%

Forma general Polinomio general fn(x) = b 0 + b 1(x – x 0) +. . . + bn(x – x 0)(x – x 1). . . (x – xn– 1) Los coeficientes se calculan con b 0 = f(x 0) b 1 = f [x 1, x 0] b 2 = f [x 2, x 1, x 0] bn = f [, xn– 1, . . . , x 1, x 0] Donde los paréntesis cuadrados se denominan diferencias divididas finitas. La n-ésima diferencia dividida finita es: Se conoce como polinomio de interpolación de Newton en diferencias divididas.

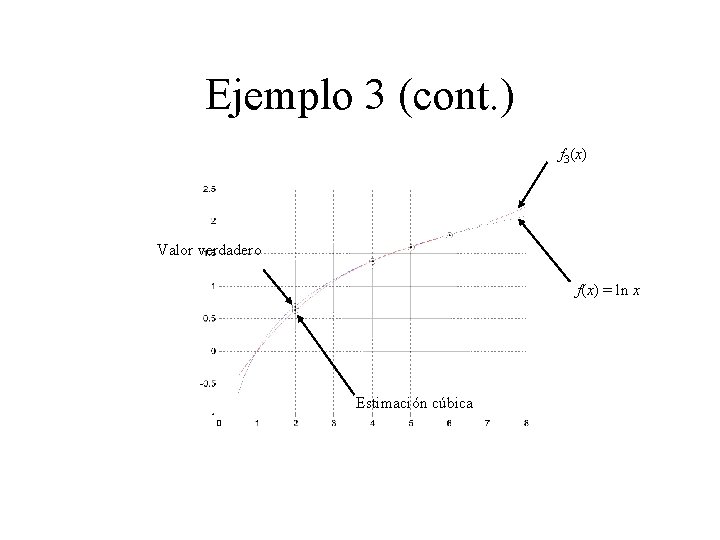
ejemplo 3 Calculemos ln 2 con ln 0, ln 4, ln 5 y ln 6, los punto que se conocen son: x 0 = 1 f(x 0) = 0 x 1 = 4 f(x 1) = 1. 386294 x 2 = 6 f(x 3) = 1. 791759 x 3 = 5 f(x 2) = 1. 609438 primeras diferencias f [x 1, x 0] = (1. 386294 – 0)/(4 – 1) = 0. 4602981 f [x 2, x 1] = (1. 791759 – 1. 386294)/(6 – 4) = 0. 2027326 f [x 3, x 2] = (1. 609438 – 1. 791759)/(5 – 6) = 0. 1823216 Segundas diferencias f [x 2, x 1, x 0] = (0. 2027326 – 0. 4602981)/(6 – 1) = – 0. 05187311 f [x 3, x 2, x 1] = (0. 1823216 – 0. 2027326)/(5 – 4) = – 0. 02041100 tercera diferencia f [x 3, x 2, x 1 , x 0] = (– 0. 02041100–(– 0. 05187311))/(5 – 1) = 0. 007865529 Polinomio f 3(x) = 0 + 0. 4602981(x – 1) – 0. 05187311(x – 1) (x – 4) + 0. 007865529(x – 1) (x – 4) (x – 6) Valor calculado con el polinomio f 3(2) = 0. 6287686

Ejemplo 3 (cont. ) f 3(x) Valor verdadero f(x) = ln x Estimación cúbica

Estimación del error Para estimar el error requerimos de un datos más (xn+1). La siguiente fórmula puede utilizarse para estimar el error. Rn = f [, xn+1, xn, . . . , x 1, x 0](x – x 0) (x – x 1). . . (x – xn)

Interpolación y polinomio de Lagrange Se trata de encontrar un polinomio de grado n que pase por los puntos (x 0, f(x 0)), (x 1, f(x 1)), . . . (xn, f(xn)), se construye un cociente Ln, k(xk) con la propiedad de que Ln, k(xi) = 0 cuando i k y Ln, k(xk) = 1 Se requiere entonces que el numerador contenga (x – x 0) (x – x 1). . . (x – xk– 1)(x – xk+1). . . (x – xn) El denominador debe coincidir con el numerador cuando x = x k.

N-ésimo polinomio interpolante de Lagrange Teorema Si x 0, x 1, x 2, . . . xn, son n+1 números distintos y si f es una función cuyos valores están dados en esos números, entonces existe un polinomio de grado a lo más n, con la propiedad de que f(xk) = P(xk) para cada k = 0, 1, 2, . . . n Este polinomio está dado por donde

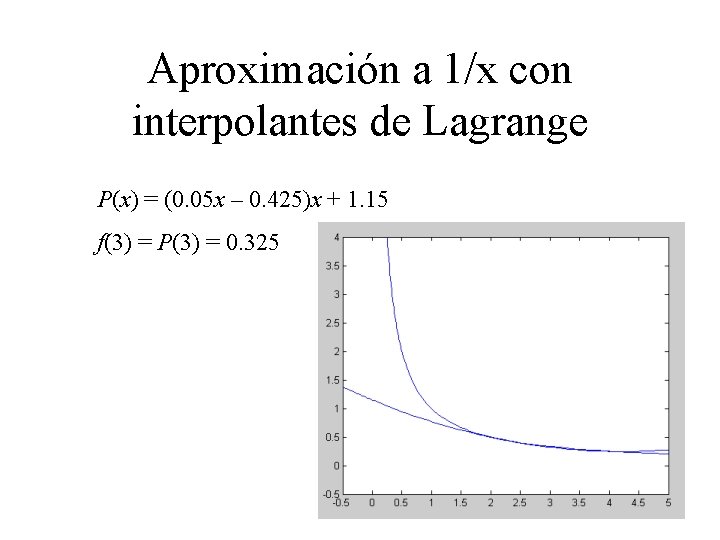
Aproximación a 1/x con interpolantes de Lagrange Usaremos x 0 = 2, x 1 = 2. 5 y x 2 = 4, para obtener un polinomio de grado 2 para 1/x. f(x 0) = 0. 5, f(x 1)= 0. 4 y f(x 2) = 0. 25. Los polinomios de Lagrange son: P(x) = 0. 5*((x– 6. 5)x+10)+0. 4*((– 4 x+24)x– 32)/3+ 0. 25*((x + 4. 5)x+5)/3 P(x) = (0. 05 x – 0. 425)x + 1. 15 = 0. 05 x 2 – 0. 425 x + 1. 15 f(3) = P(3) = 0. 325

Aproximación a 1/x con interpolantes de Lagrange P(x) = (0. 05 x – 0. 425)x + 1. 15 f(3) = P(3) = 0. 325

El error en la interpolación de Lagrange puede calcularse con

Algoritmo en Matlab function fi = Lagran_(x, f, xi) fi=zeros(size(xi)); np 1=length(f); for i=1: np 1 z=ones(size(xi)); for j=1: np 1 if i~=j, z = z. *(xi - x(j))/(x(i)-x(j)); end fi=fi+z*f(i); end return

Calcula coeficientes de P 2(x) %Calcula el polinomio interpolante de Lagrange de grado 2 function [a, b, c] = Lagrange(x 0, x 1, x 2, fx 0, fx 1, fx 2) t 0 = (x 0 - x 1)*(x 0 - x 2); t 1 = (x 1 - x 0)*(x 1 - x 2); t 2 = (x 2 - x 0)*(x 2 - x 1); a = fx 0/t 0 +fx 1/t 1 +fx 2/t 2; b = -fx 0*(x 1 + x 2)/t 0 - fx 1*(x 0 + x 2)/t 1 fx 2*(x 0 + x 1)/t 2; c = fx 0*x 1*x 2/t 0 + fx 1*x 0*x 2/t 1 + fx 2*x 0*x 1/t 2;

Interpolación Inversa Tabla de valores de f (x) = 1/x. x 1 2 3 4 5 6 7 f (x) 1 0. 5 0. 3333 0. 25 0. 2 0. 1667 0. 1429 Se desea conocer el valor de x tal que f (x) = 0. 3. El problema se resuelve definiendo un polinomio de interpolación de grado 2 con los puntos (2, 0. 5), (3, 0. 3333) y (4, 0. 25) y resolviendo la ecuación: f (x) = 0. 3 = 1. 08333 – 0. 375 x + 0. 041667 x 2 Lo que da x = 5. 704158 y x = 3. 295842, el valor real es 3. 333.

Trazadores (Splines) Dados n +1 puntos podemos construir un polinomio de grado n para interpolar valores dentro del intervalo. También se pueden usar líneas rectas entre cada par de puntos para hacer interpolación lineal entre ellos o polinomios cuadráticos o cúbicos. Tales interpoladores se llaman trazadores lineales, cuadráticos y cúbicos, respectivamente. La ventaja de los trazadores es que no presentan el efecto de oscilación de los polinomios de alto grado.

f (x) x f (x)

Trazadores lineales Para los trazadores lineales se definen rectas entre cada intervalo para calcular los valores intermedios. f (x) = f (x 0) + m 0(x – x 0) x 0 <= x 1 f (x) = f (x 1) + m 1(x – x 0) x 1 <= x 2 f (x) = f (x 0) + mn– 1 (x – x 0) xn– 1 <= xn Los valores de mi se calculan con:

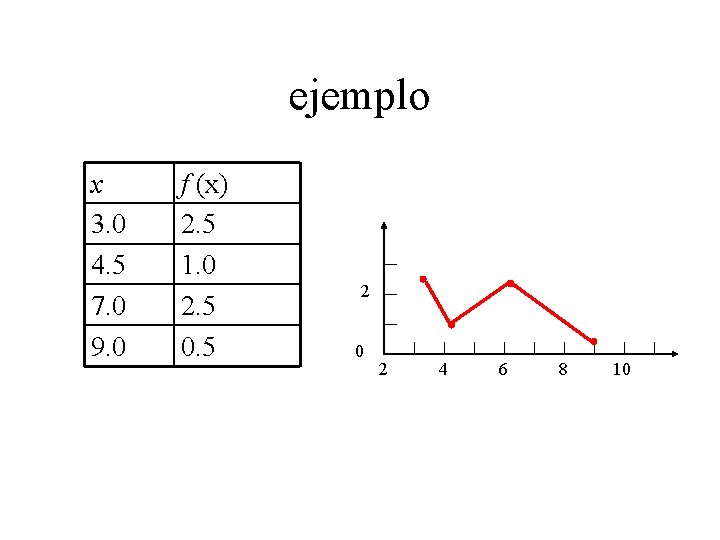
ejemplo x 3. 0 4. 5 7. 0 9. 0 f (x) 2. 5 1. 0 2. 5 0. 5 2 0 2 4 6 8 10

Trazadores cuadráticos El polinomio en cada intervalo es de la forma: fi(x) = ai x 2 + bi x + ci Para encontrar los ai , bi , ci se deben cumplir las siguientes condiciones: 1. Los valores de la función deben ser iguales en los nodos interiores, 2 n – 2 ecuaciones. 2. La primera y última función debe pasar por los extremos, 2 ecuaciones. 3. Las primeras derivadas en los nodos interiores deben ser iguales, n – 1 ecuaciones. O sea: 2 ai – 1 xi– 1 + bi – 1 = 2 ai xi– 1 + bi 4. Suponer derivada 0 en el primer punto. a 1 = 0

ejemplo x 3. 0 4. 5 7. 0 9. 0 f (x) 2. 5 1. 0 2. 5 0. 5 Encontrar f (5)

La condición 1 genera las siguientes ecuaciones: 20. 25 a 1 + 4. 5 b 1 + c 1 = 1. 0 20. 25 a 2 + 4. 5 b 2 + c 2 = 1. 0 49 a 2 + 7 b 2 + c 2 = 2. 5 49 a 3 + 7 b 3 + c 3 = 2. 5 La condición 2 da las siguientes ecuaciones 9 a 1 + 3 b 1 + c 1 = 2. 5 81 a 3 + 9 b 3 + c 3 = 0. 5 La condición 3 genera: 9 a 1 + b 1 = 9 a 2 + b 2 14 a 2 + b 2 = 14 a 3 + b 3

El sistema resultante es: La solución es: a 1 = 0 b 1 = – 1 c 1 = 5. 5 a 2 = 0. 64 b 2 = – 6. 67 c 2 = 18. 46 a 3 = – 1. 6 b 3 = – 24. 6 c 3 = 91. 3 f(5) = 0. 64(5)2 – 6. 67(5) +18. 46 = 1. 11

yi = ppval (pp, xi) - Evalúa polinomio a trozos pp en los puntos xi. Si pp. d es un escalar mayor que 1, o un arreglo, entonces el valor regresado yi será un arreglo que es d 1, . . . , dk, length (xi). pp = spline (x, y) yi = spline (x, y, xi) Regresa los interpolantes cúbicos de y en los puntos x. Si se llama con dos argumentos, regresa los trozos polinomicos pp que ueden ser evaluados con ppval. Si se llama con tres parámetros, evalúa el los puntos xi.

Splines cúbicos Aplicando las condiciones de continuidad del spline S y de las derivadas primera S' y segunda S'', es posible encontrar la expresión analítica del spline. Donde hi = xi+1 – xi y z 0, z 1, … , zn son incognitas.

Aplicando las condiciones de continuidad se llega a La ecuación anterior, genera un sistema de n– 1 ecuaciones lineales con n+1 incógnitas. donde

Los valores del spline S se calculan eficientemente con Donde

Los coeficientes de los polinomios se pueden calcular con: c 1 = yi – xi D c 2 = D – xi E c 3 = E – xi A c 4 = A Para obtener: fi (x) = c 1 + c 2 x + c 3 x 2 + c 4 x 3 Donde

Guión en Mat. Lab %encuentra los trazadores cúbicos para un conjunto de puntos x, y % x - vector con los n valores de x % y - vector con los n valores de y % w - matriz de n-1 por 4 con los coeficientes de los polinomios cúbicos function w = spline 3(x, y) [dummy n] = size(x); for i = 1: n-1 h(i) = x(i+1)-x(i); b(i) = 6*(y(i+1)-y(i))/h(i); end u(2) = 2*(h(1)+h(2)); v(2) = b(2)-b(1); for i = 3: n-1 u(i) = 2*(h(i)+h(i-1))-h(i-1)^2/u(i-1); v(i) = b(i)-b(i-1)-h(i-1)*v(i-1)/u(i-1); end

z(n) = 0; for i = n-1: 2; z(i) = (v(i)-h(i)*z(i+1))/u(i); end z(1) = 0; for i = 1: n-1 A = (z(i+1)-z(i))/6/h(i); B = z(i)/2; C = -h(i)*z(i+1)/6 -h(i)*z(i)/3+(y(i+1)-y(i))/h(i); D = C-x(i)*B+A*x(i)^2; E = B-2*x(i)*A; w(i, 4) = y(i)-x(i)*D; w(i, 3) = D-x(i)*E; w(i, 2) = E-x(i)*A; w(i, 1) = A; end

Ejemplo