International Baccalaureate Mathematical Studies International Baccalaureate Mathematical Studies

International Baccalaureate Mathematical Studies International Baccalaureate Mathematical Studies International Baccalaureate Mathematical Studies Learning outcomes International Baccalaureate Mathematical Studies International Baccalaureate This work will help you Mathematical Studies International Baccalaureate Mathematical Studies 1. To draw a scatter diagrams. Studies International Baccalaureate Mathematical Studieslines International Baccalaureate 2. Draw linear regression y on x and x on y and Mathematicalwork Studies International Baccalaureate Mathematical Studies out their equations. International Baccalaureate Mathematical Studies International 3. Identify the types. Studies of correlation and calculate Baccalaureate Mathematical International Baccalaureate correlation coefficient. Mathematicalproduct Studiesmoment International Baccalaureate Mathematical Studies International Baccalaureate Studies International 4. Use technology. Mathematical to find all of the above. Baccalaureate Mathematical Studies International Baccalaureate Mathematical Studies Linear regression and correlation

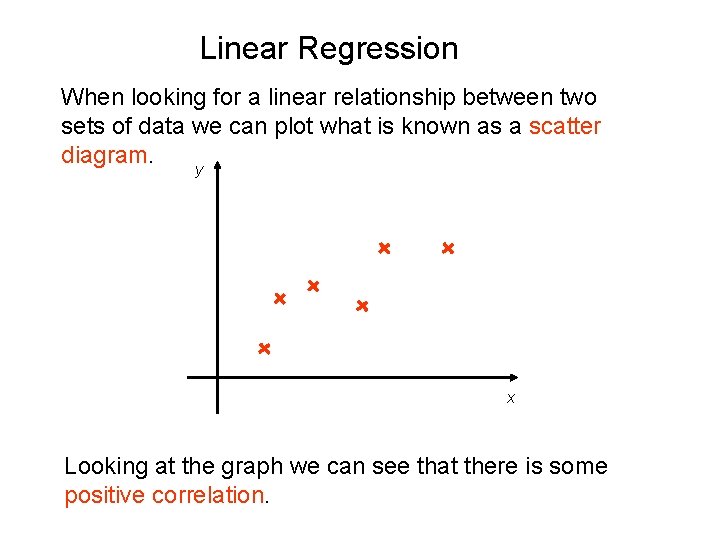
Linear Regression When looking for a linear relationship between two sets of data we can plot what is known as a scatter diagram. y x Looking at the graph we can see that there is some positive correlation.

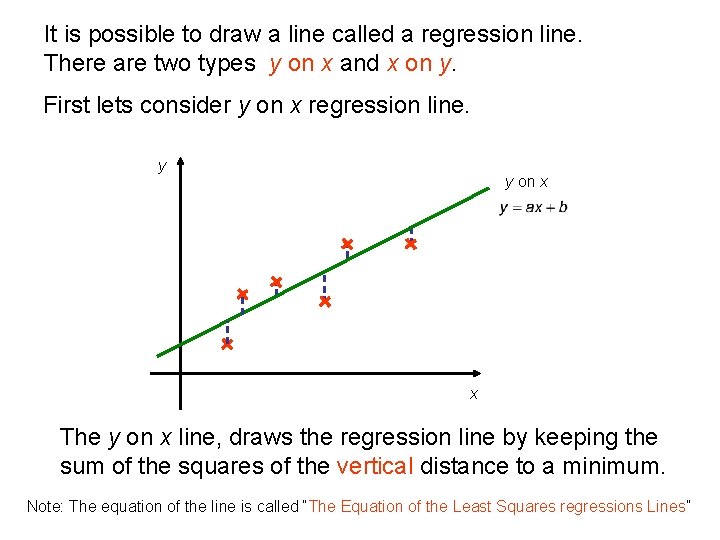
It is possible to draw a line called a regression line. There are two types y on x and x on y. First lets consider y on x regression line. y y on x x The y on x line, draws the regression line by keeping the sum of the squares of the vertical distance to a minimum. Note: The equation of the line is called “The Equation of the Least Squares regressions Lines”

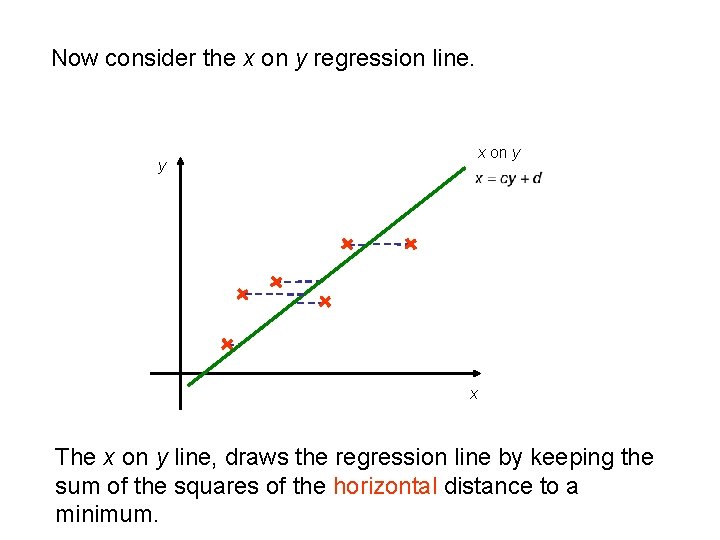
Now consider the x on y regression line. y x on y x The x on y line, draws the regression line by keeping the sum of the squares of the horizontal distance to a minimum.

Drawing both graphs on the same graph we have x on y y y on x x We should note that both graphs will pass through the means of both sets of data, .

It is possible to calculate the equations of the y on x and x on y regression lines. Important formulae y on x regression line is of the form calculated by using the formula. Where and can be is called the covariance and links the x and y data. is the variance of the x data

x on y regression line is of the form calculated by using the formula. Where and can be is called the covariance and links the x and y data. is the variance of the y data

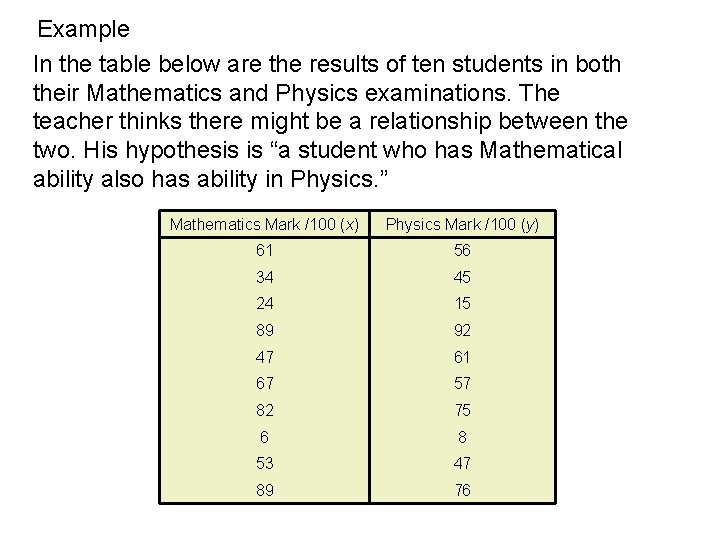
Example In the table below are the results of ten students in both their Mathematics and Physics examinations. The teacher thinks there might be a relationship between the two. His hypothesis is “a student who has Mathematical ability also has ability in Physics. ” Mathematics Mark /100 (x) Physics Mark /100 (y) 61 56 34 45 24 15 89 92 47 61 67 57 82 75 6 8 53 47 89 76

Drawing a scatter graph x y 61 56 34 45 24 15 89 92 47 61 67 57 82 75 6 8 53 47 89 76

Maths/100

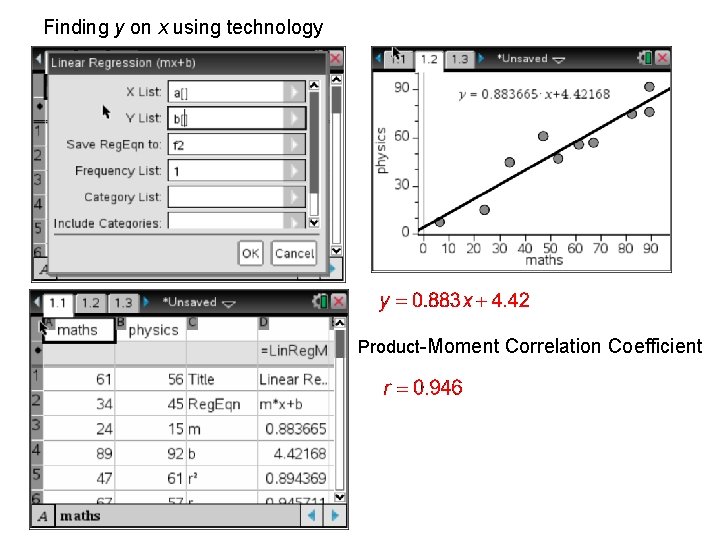
Finding y on x using technology Product-Moment Correlation Coefficient

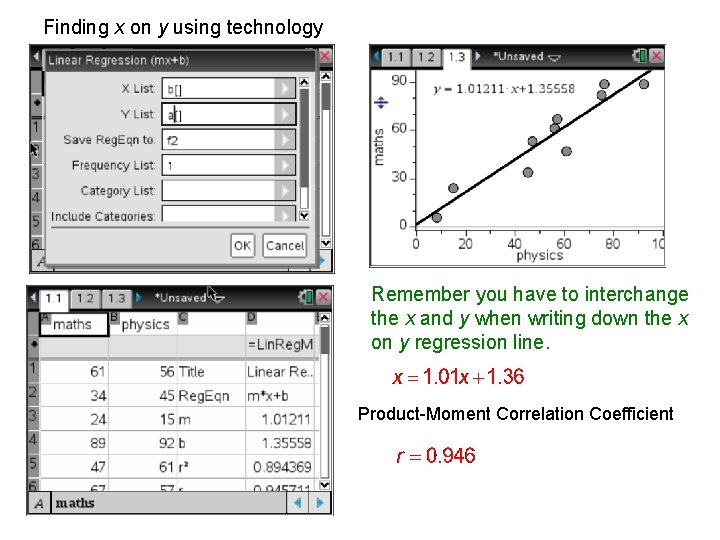
Finding x on y using technology Remember you have to interchange the x and y when writing down the x on y regression line. Product-Moment Correlation Coefficient

Example In the table below are the results of ten students in both their Mathematics and Physics examinations. The teacher thinks there might be a relationship between the two. His hypothesis is “a student who has Mathematical ability also has ability in Physics. ” Mathematics Mark /100 (x) Physics Mark /100 (y) 61 56 34 45 24 15 89 92 47 61 67 57 82 75 6 8 53 47 89 76

Now calculating the regression lines x y 61 56 34 45 5. 8 -21. 2 2. 8 -8. 2 24 15 -31. 2 89 92 47 33. 64 449. 44 7. 84 67. 24 16. 24 173. 84 -38. 2 973. 44 1459. 24 1191. 84 33. 8 38. 8 1142. 44 1505. 44 1311. 44 61 -8. 2 7. 8 67. 24 60. 84 -63. 96 67 57 11. 8 3. 8 139. 24 14. 44 44. 84 82 75 26. 8 21. 8 718. 24 475. 24 6 8 -49. 2 -45. 2 2420. 64 2043. 04 584. 24 2223. 84 53 47 -2. 2 -6. 2 38. 44 89 76 33. 8 22. 8 4. 84 1142. 44 519. 84 13. 64 770. 64 552 532 7091. 60 6191. 60 6266. 60

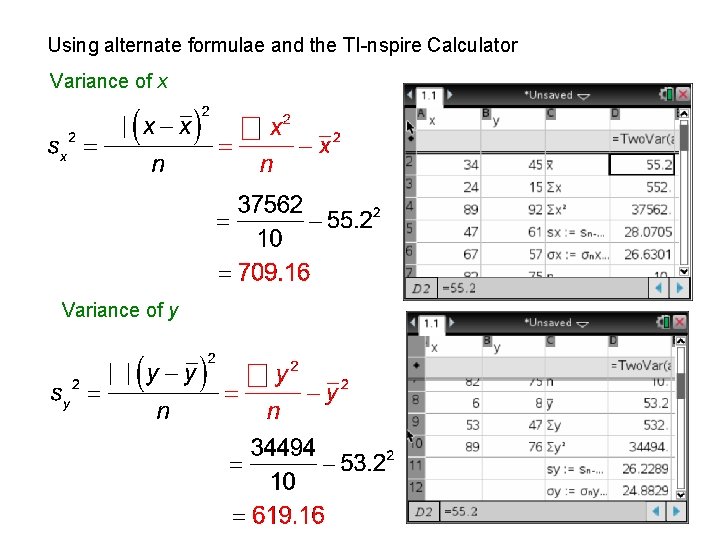
Using alternate formulae and the TI-nspire Calculator Variance of x Variance of y

Covariance Having done the 2 -variable stats calculation the actual value of variance (which is the standard deviation squared) can be found using the “Var” menu on the calculator.

For regression line y on x which has form

For regression line x on y which has form

Plotting both lines on the scatter diagram y on x, and for x on y, Note: For x on y line, remember to rearrange it into the following form before trying to plot x on y y on x

Correlation We need a way to determine if there is linear correlation or not. So we calculate what is known as the Product-Moment Correlation Coefficient (r). (covariance), (standard deviation of x) (standard deviation of y). We can see that the quantity r from the following five sets of data above tells us something about the degree of scatter of the two sets of data, if we are looking for a linear relationship.

Table 1 x 0 5 10 15 20 25 30 35 y 38 28 26 19 17 8 5 1 y on x x on y The product moment correlation coefficient In table 1 we notice that the two regressions lines (y on x and x on y) nearly coincide and that as the x-data increases the y-data decreases. The value of r is -0. 990, which is close to – 1. Here we have what is called strong negative linear correlation.

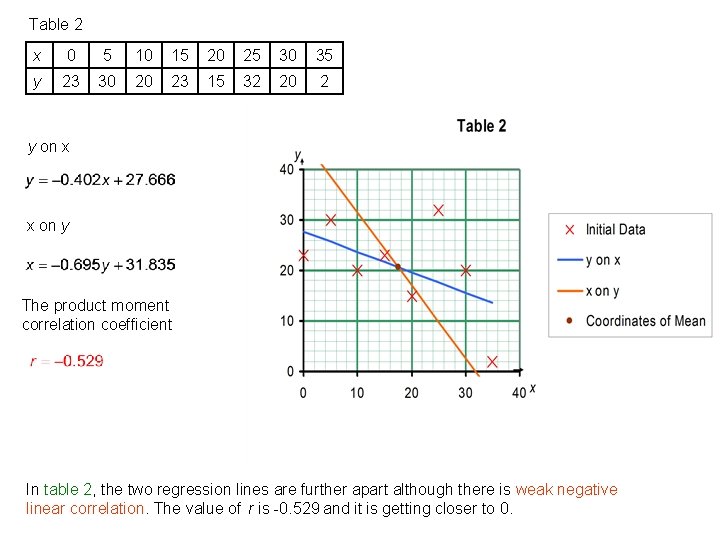
Table 2 x 0 5 10 15 20 25 30 35 y 23 30 20 23 15 32 20 2 y on x x on y The product moment correlation coefficient In table 2, the two regression lines are further apart although there is weak negative linear correlation. The value of r is -0. 529 and it is getting closer to 0.

Table 3 x 0 5 10 15 20 25 30 35 y 5 31 19 23 30 32 20 6 y on x x on y The product moment correlation coefficient In table 3, the two regression lines are virtually perpendicular and there is no linear correlation. The value of r is -. 00548 and it is very close to 0.

Table 4 x 0 5 10 15 20 25 30 35 y 12 17 23 9 12 38 18 40 y on x x on y The product moment correlation coefficient In table 4, the two regression lines are further apart but we notice that as the x-data increases the y-data increases. We say there is weak positive linear correlation. The value of r is 0. 612 and it is moving away from 0 and getting closer to 1.

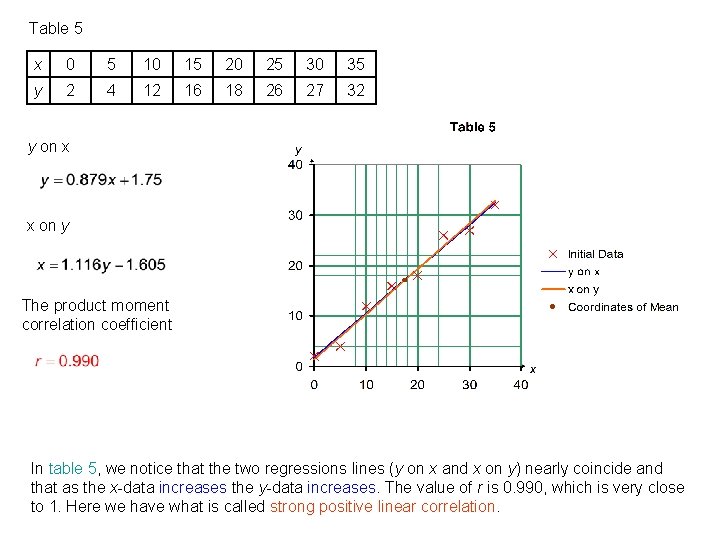
Table 5 x 0 5 10 15 20 25 30 35 y 2 4 12 16 18 26 27 32 y on x x on y The product moment correlation coefficient In table 5, we notice that the two regressions lines (y on x and x on y) nearly coincide and that as the x-data increases the y-data increases. The value of r is 0. 990, which is very close to 1. Here we have what is called strong positive linear correlation.

The value of r determines the degree of linear scatter of the two sets of data and - indicates that the data have perfect negative linear correlation, - indicates that the data has no linear correlation, - indicates that the data have perfect positive linear correlation. r is called Product-Moment Correlation Coefficient.

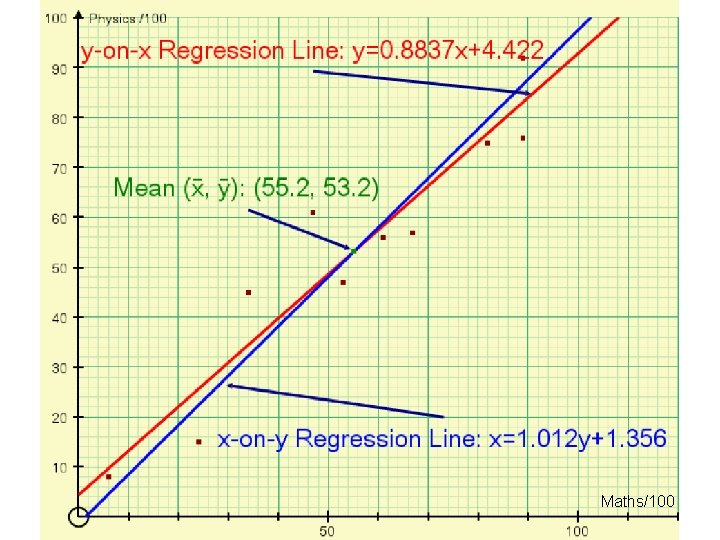
Returning to our example x on y y on x So we can conclude that as r is close to 1, that the results show that his hypothesis that “a student who has Mathematical ability also has ability in Physics’” might be true.

Maths/100