Internal Flow Entrance Conditions Must distinguish between entrance

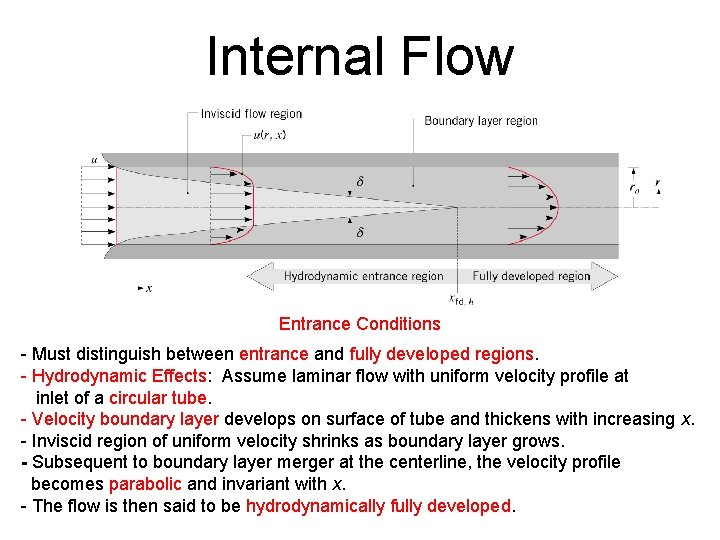
Internal Flow Entrance Conditions - Must distinguish between entrance and fully developed regions. - Hydrodynamic Effects: Assume laminar flow with uniform velocity profile at inlet of a circular tube. - Velocity boundary layer develops on surface of tube and thickens with increasing x. - Inviscid region of uniform velocity shrinks as boundary layer grows. - Subsequent to boundary layer merger at the centerline, the velocity profile becomes parabolic and invariant with x. - The flow is then said to be hydrodynamically fully developed.

Hydrodynamic Entry Length For a circular tube, entry lengths depend on whether the flow is laminar or turbulent, which, in turn, depend on Reynolds number. um is the mean fluid velocity over the tube cross section. The hydraulic diameter is defined as in which case, Onset of turbulence occurs at a critical Reynolds number of Fully turbulent conditions exist for Hydrodynamic Entry Length

The Mean Velocity Absence of well-defined free stream conditions, as in external flow, and hence a reference velocity u∞ or temperature T∞, dictates the use of a cross-sectional mean velocity um and temperature Tm for internal flow. Linkage of mean velocity to mass flow rate:

Velocity profile in the fully developed region For the laminar flow of incompressible, constant property fluid in the fully developed region of a circular tube.

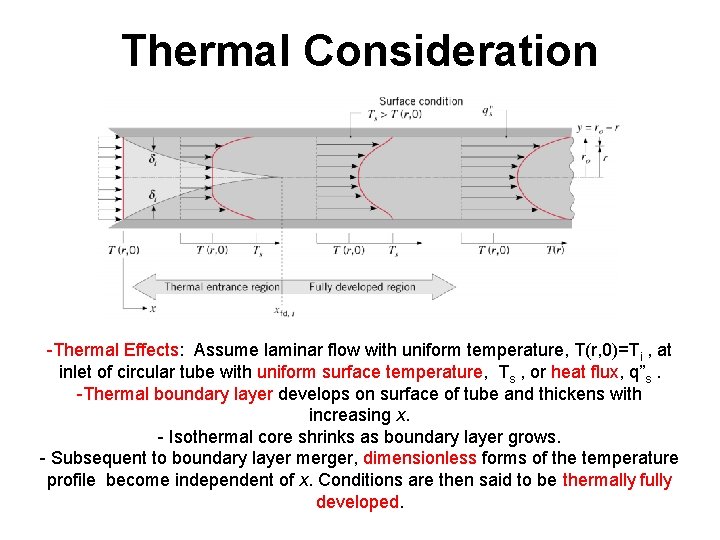
Thermal Consideration -Thermal Effects: Assume laminar flow with uniform temperature, T(r, 0)=Ti , at inlet of circular tube with uniform surface temperature, Ts , or heat flux, q”s. -Thermal boundary layer develops on surface of tube and thickens with increasing x. - Isothermal core shrinks as boundary layer grows. - Subsequent to boundary layer merger, dimensionless forms of the temperature profile become independent of x. Conditions are then said to be thermally fully developed.

Thermal Entry Length

Mean Temperature Linkage of mean temperature (bulk T. , mass average T. , mixing –cup T. ) to thermal energy transport associated with flow through a cross section: Newton’s Law of Cooling for the Local Heat Flux: What is the essential difference between use of Tm for internal flow and T∞ for external flow?

Fully Developed Flow • Requirement for fully developed thermal conditions: • Effect on the local convection coefficient: Hence, assuming constant properties, In thermally fully developed flow of a fluid with constant properties, the local convection coeff. is a constant, independent of x.

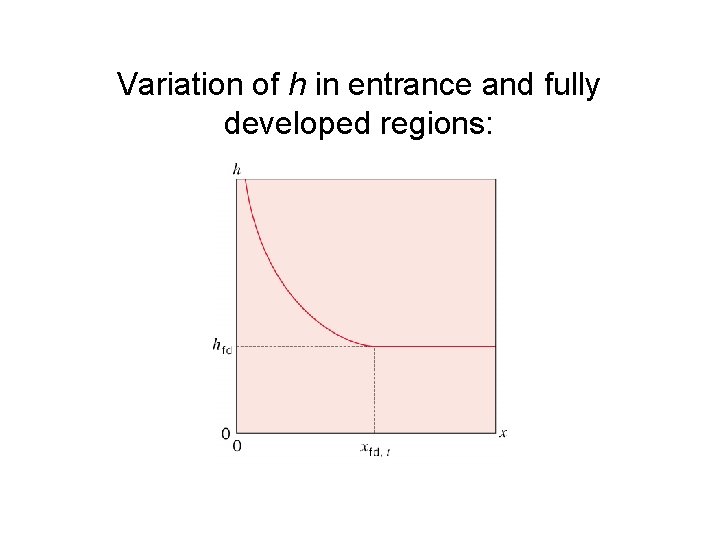
Variation of h in entrance and fully developed regions:

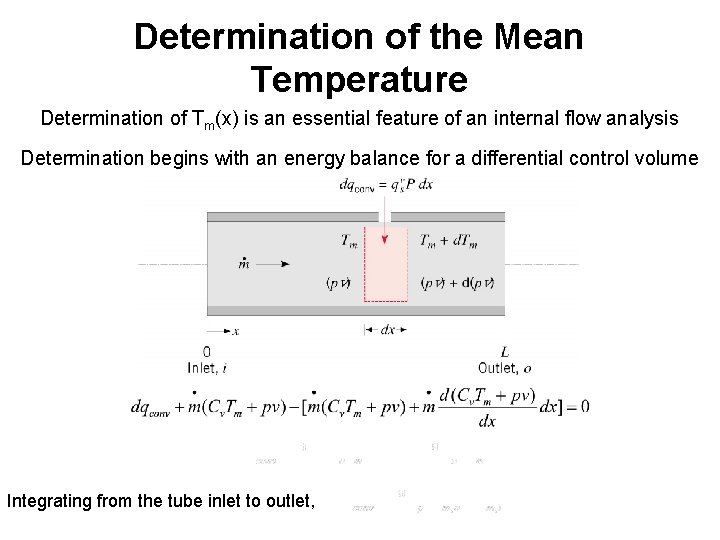
Determination of the Mean Temperature Determination of Tm(x) is an essential feature of an internal flow analysis Determination begins with an energy balance for a differential control volume Integrating from the tube inlet to outlet,

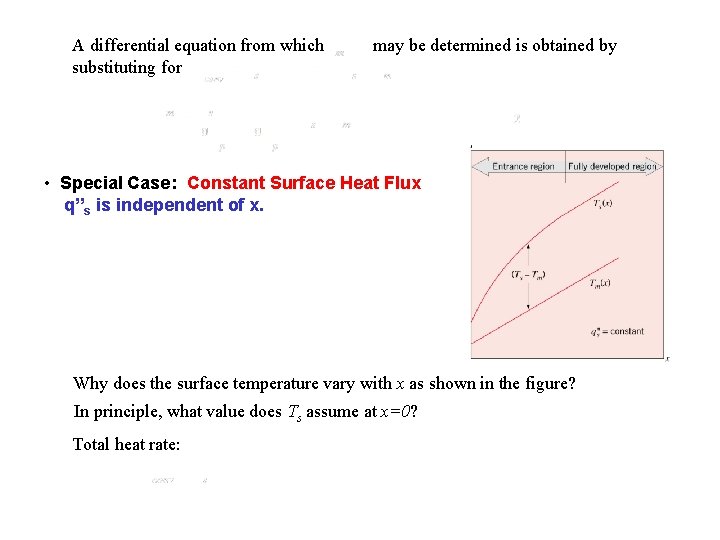
A differential equation from which substituting for may be determined is obtained by • Special Case: Constant Surface Heat Flux q”s is independent of x. Why does the surface temperature vary with x as shown in the figure? In principle, what value does Ts assume at x=0? Total heat rate:

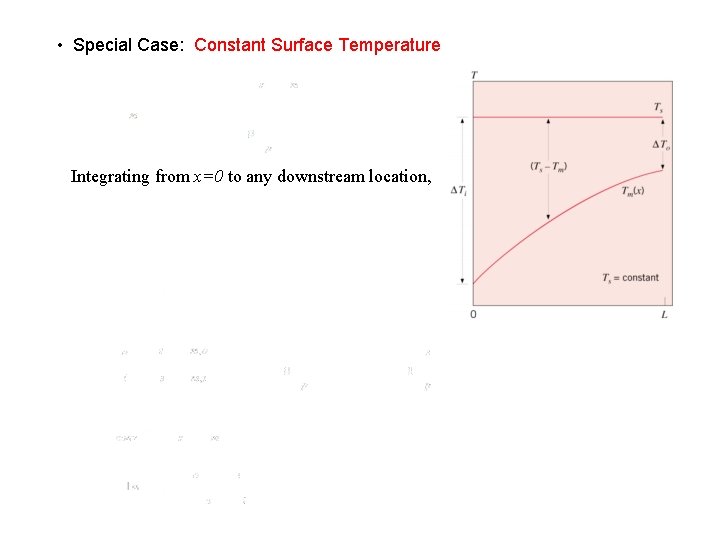
• Special Case: Constant Surface Temperature Integrating from x=0 to any downstream location,